6.4: Composición de las funciones

PREVIAR ACTIVIDAD\(\PageIndex{1}\): Constructing a New Function

Vamos\(A = \{a, b, c, d\}\),\(B = \{p, q, r\}\), y\(C = \{s, t, u, v\}\). El diagrama de flechas en la Figura 6.6 muestra dos funciones:\(f: A \to B\) y\(g: B \to C\). Observe que si\(x \in A\), entonces\(f(x) \in B\). Ya que\(f(x) \in B\), podemos aplicar la función\(g\) a\(f(x)\), y obtenemos\(g(f(x))\), que es un elemento de\(C\).

Usando este proceso, determinar\(g(f(a))\),\(g(f(b))\),\(g(f(c))\), y\(g(f(d))\). Luego explique cómo podemos usar esta información para definir una función de\(A\) a\(C\).

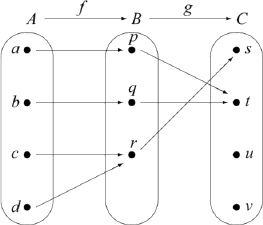
Figura 6.6: Diagrama de flechas que muestra dos funciones

PREVIAR ACTIVIDAD\(\PageIndex{1}\): Verbal Descriptions of Functions

Los resultados de la mayoría de las funciones reales que hemos estudiado en cursos previos de matemáticas han sido determinados por expresiones matemáticas. En muchos casos, es posible utilizar estas expresiones para dar descripciones verbales paso a paso de cómo calcular las salidas. Por ejemplo, si

\(f: \mathbb{R} \to \mathbb{R}\)se define por\(f(x) = (3x + 2)^3\),

podríamos describir cómo calcular las salidas de la siguiente manera:

Paso	Descripción Verbal	Resultado Simbólico
1	Elija una entrada.	\(x\)
2	Multiplicar por 3.	\(3x\)
3	Agregar 2.	\(3x + 2\)
4	Cube el resultado.	\((3x + 3)^3\)

Descripciones verbales completas paso a paso para cada una de las siguientes funciones.

1. \(f: \mathbb{R} \to \mathbb{R}\)por\(f(x) = \sqrt{3x^2 + 2}\), para cada uno\(x \in \mathbb{R}\).
2. \(g: \mathbb{R} \to \mathbb{R}\)por\(g(x) = \sin(3x^2 + 2)\), para cada uno\(x \in \mathbb{R}\).
3. \(h: \mathbb{R} \to \mathbb{R}\)por\(h(x) = e^{3x^2 + 2}\), para cada uno\(x \in \mathbb{R}\).
4. \(G: \mathbb{R} \to \mathbb{R}\)por\(G(x) = \ln(x^4 + 3)\), para cada uno\(x \in \mathbb{R}\).
5. \(k: \mathbb{R} \to \mathbb{R}\)por\(k(x) = \sqrt[3] {\dfrac{\sin(4x + 3)}{x^2 + 1}}\), para cada uno\(x \in \mathbb{R}\).

Composición de Funciones

Hay varias formas de combinar dos funciones existentes para crear una nueva función. Por ejemplo, en cálculo, aprendimos a formar el producto y cociente de dos funciones y luego a usar la regla de producto para determinar la derivada de un producto de dos funciones y la regla de cociente para determinar la derivada del cociente de dos funciones. La regla de la cadena en cálculo se utilizó para determinar la derivada de la composición de dos funciones, y en esta sección, nos centraremos únicamente en la composición de dos funciones. Luego consideraremos algunos resultados sobre las composiciones de inyecciones y suryecciones.

La idea básica de la composición de funciones es que cuando es posible, la salida de una función\(f\) se utiliza como entrada de una función\(g\). Esto puede denominarse “\(f\)seguido por\(g\)” y se llama la composición de\(f\) y\(g\). En cursos previos de matemáticas, se utilizó esta idea para determinar una fórmula para la composición de dos funciones reales.

Por ejemplo, si

\(f(x) = 3x^2 + 2\)y\(g(x) = sin x\)

entonces podemos calcular de la\(g(f(x))\) siguiente manera:

\[\begin{array} {rcl} {g(f(x))} &= & {g(3x^2 + 2)}\\ {} &= & {sin(3x^2 + 2).} \end{array}\]

En este caso,\(f(x)\), la salida de la función\(f\), se utilizó como entrada para la función\(g\). Damos ahora la definición formal de la composición de dos funciones.

Definición: función compuesta

Dejar\(A\),\(B\), y\(C\) ser conjuntos no vacíos, y dejar\(f: A \to B\) y\(g: B \to C\) ser funciones. La composición de\(f\) y\(g\) es la función\(g \circ f: A \to C\) definida por

\((g \circ f)(x) = g(f(x))\)

para todos\(x \in A\). A menudo nos referimos a la función\(g \circ f\) como una función compuesta.

Es útil pensar en la función compuesta\(g \circ f\) como "\(f\)seguida de\(g\)”. Entonces nos referimos\(f\) como la función interna y\(g\) como la función externa.

Composición y diagramas de flecha

El concepto de la composición de dos funciones se puede ilustrar con diagramas de flecha cuando el dominio y el codominio de las funciones son conjuntos pequeños y finitos. Aunque entonces no se utilizó el término “composición”, esto se hizo en Preview Activity\(\PageIndex{1}\), y aquí se da otro ejemplo.

Vamos\(A = \{a, b, c, d\}\),\(B = \{p, q, r\}\), y\(C = \{s, t, u, v\}\). El diagrama de flechas en la Figura 6.7 muestra dos funciones:\(f: A \to B\) y\(g: B \to C\).

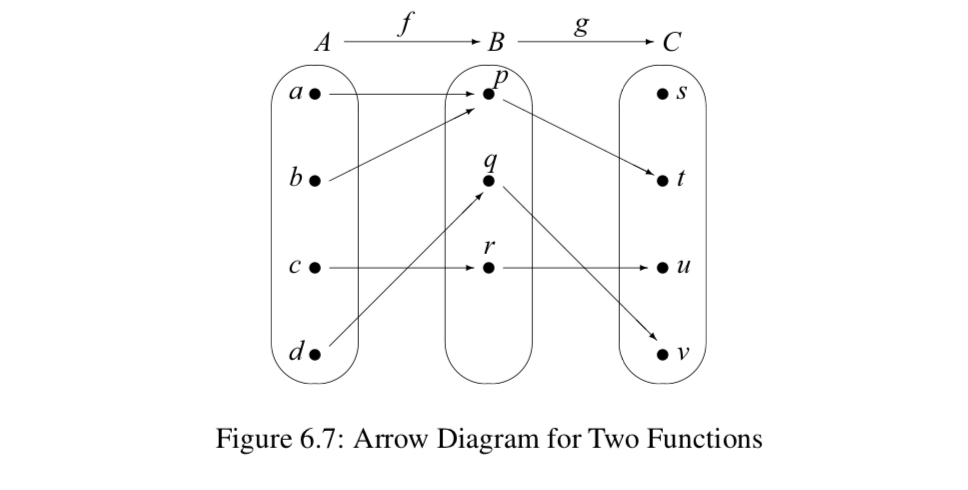
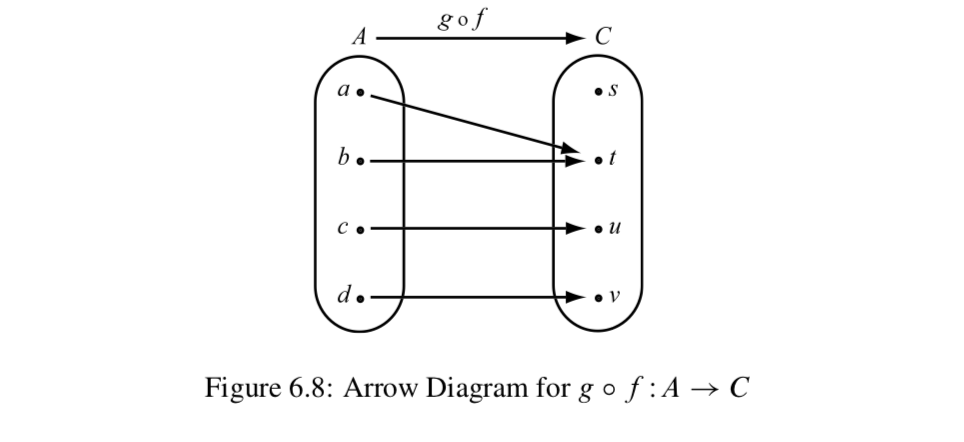
Si seguimos las flechas desde el conjunto\(A\) hasta el conjunto\(C\), usaremos las salidas de\(f\) como entradas de\(g\), y obtendremos el diagrama de flechas del\(A\) al que\(C\) se muestra en la Figura 6.8. Este diagrama representa la composición de\(f\) seguido de\(g\).

Comprobación de progreso 6.17 (La composición de dos funciones)

Dejar\(A = \{a, b, c, d\}\) y\(B = \{1, 2, 3\}\). Defina la función\(f\) y de\(g\) la siguiente manera:

\(f: A \to B\)definido por\(f(a) = 2\),\(f(b) = 3\),\(f(c) = 1\), y\(f(d) = 2\).

\(g: A \to B\)definido por\(g(1) = 3\). \(g(2) = 1\), y\(g(3) = 2\).

Crear diagramas de flecha para la función\(f\),\(g\),\(g \circ f\), y\(g \circ g\).

Responder

Agrega textos aquí. No elimine primero este texto.

Funciones de descomposición

Utilizamos la regla de la cadena en el cálculo para encontrar la derivada de una función compuesta. El primer paso en el proceso es reconocer una función dada como una función compuesta. Esto se puede hacer de muchas maneras, pero el trabajo en Preview Activity se\(\PageIndex{2}\) puede utilizar para descomponer una función de una manera que funcione bien con la regla de la cadena. El uso de los términos “función interna” y “función externa” también puede ser útil. La idea es que usemos el último paso en el proceso para representar la función externa, y los pasos anteriores a eso para representar la función interna. Entonces para la función,

\(f: \mathbb{R} \to \mathbb{R}\)por\(f(x) = (3x + 2)^3\),

el último paso en la tabla de descripción verbal fue el cubo del resultado. Esto significa que usaremos la función\(g\) (la función de cubo) como la función externa y usaremos los pasos anteriores como la función interna. Vamos a denotar la función interna por\(h\). Entonces dejamos pasar\(h: \mathbb{R} \to \mathbb{R}\)\(h(x) = 3x + 2\) y\(g: \mathbb{R} \to \mathbb{R}\) pasar\(g(x) = x^3\). Entonces

\[\begin{array} {rcl} {(g \circ h)(x)} &= & {g(h(x))} \\ {} &= & {g(3x + 2)} \\ {} &= & {(3x + 2)^3} \\ {} &= & {f(x).} \end{array}\]

Eso lo vemos\(g \circ h = f\) y, de ahí, hemos “descompuesto” la función\(f\). Cabe señalar que existen otras formas de escribir la función\(f\) como una composición de dos funciones, pero la forma que se acaba de describir es la que funciona bien con la regla de la cadena. En este caso, la regla de la cadena da

\[\begin{array} {rcl} {f \prime (x)} &= & {(g \circ h)\prime (x)} \\ {} &= & {g \prime (h(x)) h \prime(x)} \\ {} &= & {3(h(x))^2 \cdot 3} \\ {} &= & {g(3x + 2)^2} \end{array}\]

Comprobación de Progreso 6.18 (Funciones de Descomposición

Escribir cada una de las siguientes funciones como la composición de dos funciones.

1. \(F: \mathbb{R} \to \mathbb{R}\)por\(F(x) = (x^2 + 3)^3\)
2. \(G: \mathbb{R} \to \mathbb{R}\)por\(G(x) = In(x^2 + 3)\)
3. \(f: \mathbb{Z} \to \mathbb{Z}\)por\(f(x) = |x^2 - 3|\)
4. \(g: \mathbb{R} \to \mathbb{R}\)por\(g(x) = cos(\dfrac{2x - 3}{x^2 + 1})\)

Responder

Agrega textos aquí. No elimine primero este texto.

Teoremas sobre las funciones compuestas

Si\(f: A \to B\) y\(g: B \to C\), entonces podemos formar la función compuesta\(g \circ f: A \to C\). En la Sección 6.3, aprendimos sobre inyecciones y sobreyecciones. Ahora exploramos qué tipo de función\(g \circ f\) será si las funciones\(f\) y\(g\) son inyecciones (o suryecciones).

Comprobación de Progreso 6.19: Composiciones de Inyecciones y Suryecciones

Aunque se pueden usar otras representaciones de funciones, será útil usar diagramas de flecha para representar las funciones en esta comprobación de progreso. Utilizaremos los siguientes conjuntos:

\(A = \{a, b, c\}\),\(B = \{p, q, r\}\),\(C = \{u,v, w, x\}\), y\(D = \{u, v\}\).

1. Dibuja un diagrama de flechas para una función\(f: A \to B\) que es una inyección y un diagrama de flechas para una función\(g: B \to C\) que es una inyección. En este caso, ¿la función compuesta es\(g \circ f: A \to C\) una inyección? Explicar.
2. Dibuja un diagrama de flechas para una función\(f: A \to B\) que sea una suryección y un diagrama de flechas para una función\(g: B \to D\) que sea una suryección. En este caso, ¿la función compuesta es\(g \circ f: A \to D\) una sobreyección? Explicar.
3. Dibuja un diagrama de flechas para una función\(f: A \to B\) que sea una biyección y un diagrama de flechas para una función\(g: B \to A\) que sea una biyección. En este caso, ¿la función compuesta es\(g \circ f: A \to A\) biyección? Explicar.

Responder

Agrega textos aquí. No elimine primero este texto.

En la Comprobación de Progreso 6.19, exploramos algunas propiedades de las funciones compuestas relacionadas con inyecciones, suryecciones y biyecciones. El siguiente teorema contiene resultados que estas exploraciones se pretendieron ilustrar. Algunas de las pruebas se incluirán en los ejercicios.

Teorema 6.20.

Dejar\(A\),\(B\), y\(C\) ser conjuntos no vacíos y asumir que\(f: A \to B\) y\(g: B \to C\).

1. Si\(f\) y\(g\) son ambas inyecciones, entonces\((g \circ f): A \to C\) es una inyección.
2. Si\(f\) y\(g\) son ambas sobreyecciones, entonces\((g \circ f): A \to C\) es una sobrejección.
3. Si\(f\) y\(g\) son ambas bijecciones, entonces\((g \circ f): A \to C\) es una bijección.

Prueba

El comprobante de la Parte (1) es Ejercicio (6).

La parte (3) es una consecuencia directa de las dos primeras partes. Discutiremos un proceso para construir una prueba de la Parte (2). Usando el proceso hacia adelante y hacia atrás, primero miramos la conclusión de la declaración condicional en la Parte (2). El objetivo es demostrar que\(g \circ f\) es una sobrejección. Ya que\((g \circ f): A \to C\), esto equivale a demostrar que

Para todos\(c \in C\), existe\(a \in A\) tal que\((g \circ f)(a) = c\).

Dado que esta afirmación en el proceso hacia atrás utiliza un cuantificador universal, usaremos el método choose-an-element y elegiremos un elemento arbitrario\(c\) en el conjunto\(C\). El objetivo ahora es encontrar un\(a \in A\) tal que\((g \circ f)(a) = c\).

Ahora podemos mirar las hipótesis. En particular, estamos asumiendo que ambos\(f: A \to B\) y\(g: B \to C\) son sobreyecciones. Ya que hemos elegido\(c \in C\), y\(g: B \to C\) es una sobrejección, sabemos que

existe\(b \in B\) tal que\(g(b) = c\).

Ahora,\(b \in B\) y\(f: A \to B\) es una sobrejección. De ahí

existe\(a \in A\) tal que\(f(a) = b\).

Si ahora calculamos\((g \circ f)(a)\), veremos que

\((g \circ f)(a) = g(f(a)) = g(b) = c\).

Ahora podemos escribir la prueba de la siguiente manera:

Prueba de Teorema 6.20, Parte (2)

Dejar\(A\),\(B\), y\(C\) ser conjuntos no vacíos y asumir que\(f: A \to B\) y\(g: B \to C\) son ambas subyecciones. Vamos a demostrar que\(g \circ f: A \to C\) es una sobrejección.

Dejar\(c\) ser un elemento arbitrario de\(C\). Demostraremos que existe\(a \in A\) tal que\((g \circ f)(a) = c\). Dado que\(g: B \to C\) es una sobrejección, concluimos que

existe\(b \in B\) tal que\(g(b) = c\).

Ahora,\(b \in B\) y\(f: A \to B\) es una sobrejección. De ahí

existe\(a \in A\) tal que\(f(a) = b\).

Ahora vemos que

\[\begin{align*} {(g \circ f)(a)} &= & {g(f(a))} \\ {} &= & {g(b)} \\ {} &= & {c.} \end{align*}\]

Ahora hemos demostrado que para cada\(c \in C\), existe\(a \in A\) tal eso\((g \circ f)(a) = c\), y esto prueba que\(g \circ f\) es una suryección.

Teorema 6.20 nos muestra que si\(f\) y\(g\) son ambos tipos especiales de funciones, entonces la composición de\(f\) seguida por\(g\) es también ese tipo de función.La siguiente pregunta es, “Si la composición de\(f\) seguida por\(g\) es una inyección (o surjección), podemos hacer alguna conclusiones sobre\(f\) o\(g\)?” Una respuesta parcial a esta pregunta se proporciona en el Teorema 6.21. Este teorema será investigado y probado en las Exploraciones y Actividades para esta sección. Ver Ejercicio (10).

Teorema 6.21

Dejar\(A\),\(B\), y\(C\) ser conjuntos no vacíos y asumir que\(f: A \to B\) y\(g: B \to C\).

1. Si\(g \circ f: A \to C\) es una inyección, entonces\(f: A \to B\) es una inyección.
2. Si\(g \circ f: A \to C\) es una sobreyección, entonces\(f: A \to B\) es una sobrejección.

Ejercicio 6.4

1. En nuestra definición de la composición de dos funciones,\(f\) y\(g\), requerimos que el dominio de\(g\) sea igual al codominio de\(f\). Sin embargo, a veces es posible formar la función compuesta\(g \circ f\) aunque dom (\(g\))\(\ne\) codom (\(f\)). Por ejemplo, vamos
   \[\begin{array} {lcl} {f: \mathbb{R} \to \mathbb{R}} &text{ be defined by }& {f(x) = x^2 + 1\text{, and let}} \\ {g: \mathbb{R} - \{0\} \to \mathbb{R}} &text{ be defined by }& {g(x) = \dfrac{1}{x}.} \end{array}\]
   
   (a) ¿Es posible determinar\((g \circ f) (x)\) para todos\(x \in \mathbb{R}\)? Explicar.
   b) En general, dejar\(f: A \to T\) y\(g: B \to C\). Encontrar una condición en el dominio de\(g\) (que no sea\(B = T\)) que dé como resultado una definición significativa de la función compuesta\(g \circ f: A \to C\).
2. Dejar\(h: \mathbb{R} \to \mathbb{R}\) ser definido\(h(x) = 3x + 2\) y\(g: \mathbb{R} \to \mathbb{R}\) ser definido por\(g(x) = x^3\). Determinar fórmulas para las funciones compuestas\(g \circ h\) y\(h \circ g\). ¿La función es\(g \circ h\) igual a la función\(h \circ g\)? Explicar. ¿Qué le dice esto sobre el funcionamiento de la composición de funciones?
3. A continuación se presentan fórmulas para ciertas funciones reales. Escribe cada una de estas funciones reales como la composición de dos funciones. Es decir, descomponer cada una de las funciones.
   
   a)\(F(x) = cos(e^x)\)
   b)\(G(x) = e^{cos(x)}\)
   c)\(H(x) = \dfrac{1}{sin x}\)
   d)\(K(x) = cos(e^{-x^2})\)
4. La función de identidad en un conjunto\(S\), denotada por\(I_S\), se define de la siguiente manera:\(I_S: S \to S\) por\(I_s(x) = x\) para cada uno\(x \in S\). Vamos\(f: A \to B\).
   
   a) Para cada uno\(x \in A\), determinar\((f \circ I_A)(x)\) y utilizar esto para demostrarlo\(f \circ I_A = f\).
   b) Demostrarlo\(I_B \circ f = f\).
5. (a) Dejar\(f: \mathbb{R} \to \mathbb{R}\) ser definido por\(f(x) = x^2\), dejar\(g: \mathbb{R} \to \mathbb{R}\) ser definido por\(g(x) = sin x\), y dejar\(h: \mathbb{R} \to \mathbb{R}\) ser definido por\(h(x) = \sqrt[3]{x}\).
   
   Determinar fórmulas para\([(h \circ g) \circ f] (x)\) y\([h \circ (g \circ f)](x)\).
   
   ¿Esto prueba eso\((h \circ g) \circ f = h \circ (g \circ f)\) para estas funciones particulares? Explicar.
   
   b) Ahora vamos\(A\),\(B\), y\(C\) ser conjuntos y dejar\(f: A \to B\),\(g: B \to C\), y\(h: C \to D\). \((h \circ g) \circ f = h \circ (g \circ f)\)Demuéstralo. Es decir, demostrar que la composición de funciones es una operación asociativa.
6. Demostrar Parte (1) del Teorema 6.20.
   Dejar\(A\),\(B\), y\(C\) ser conjuntos no vacíos y dejar\(f: A \to B\) y\(g: B \to C\). Si\(f\) y\(g\) son ambas inyecciones, entonces\(g \circ f\) es una inyección.
7. Para cada una de las siguientes, dar un ejemplo de funciones\(f: A \to B\) y\(g: B \to C\) que satisfagan las condiciones declaradas, o explicar por qué no existe tal ejemplo.
   
   (a) La función\(f\) es una sobreyección, pero la función no\(g \circ f\) es una suryección.
   b) La función\(f\) es una inyección, pero la función no\(g \circ f\) es una inyección.
   (c) La función\(g\) es una sobreyección, pero la función no\(g \circ f\) es una sobreyección.
   d) La función\(g\) es una inyección, pero la función no\(g \circ f\) es una inyección.
   e) La función no\(f\) es una sobreyección, sino que la función\(g \circ f\) es una sobreyección.
   (f) La función no\(f\) es una inyección, sino que la función\(g \circ f\) es una inyección.
   (g) La función no\(f\) es una inyección, sino la función\(g \circ f\) es una inyección.
   (h) La función no\(g\) es una inyección, sino que la función\(g \circ f\) es una inyección.
8. Dejar\(A\) ser un conjunto no vacío y dejar\(f: A \to A\). Para cada uno\(n \in \mathbb{N}\), definir un funciton\(f^n: A \to A\) recursivamente de la siguiente manera:\(f^1 = f\) y para cada uno\(n \in \mathbb{N}\),\(f^{n + 1} = f \circ f^n\). Por ejemplo,\(f^2 = f \circ f^1 = f \circ f\) y\(f^3 = f \circ f^2 = f \circ (f \circ f)\).
   
   (a) Dejar pasar\(f: \mathbb{R} \to \mathbb{R}\)\(f(x) = x + 1\) por cada uno\(x \in \mathbb{R}\). Para cada uno\(n \in \mathbb{N}\) y para cada uno\(x \in \mathbb{R}\), determine una fórmula para\(f^n(x)\) y use la inducción para demostrar que su fórmula es correcta.
   b) Dejar\(a, b \in \mathbb{R}\) y dejar pasar\(f: \mathbb{R} \to \mathbb{R}\)\(f(x) = ax + b\) por cada uno\(x \in \mathbb{R}\). Para cada uno\(n \in \mathbb{N}\) y para cada uno\(x \in \mathbb{R}\), determine una fórmula para\(f^n(x)\) y use la inducción para demostrar que su fórmula es correcta.
   (c) Ahora vamos a\(A\) ser un conjunto no vacío y vamos\(f: A \to A\). Utilice la inducción para demostrar que para cada uno\(n \in \mathbb{N}\),\(f^{n + 1} = f^n \circ f\). (Nota: Deberá utilizar el resultado en el Ejercicio (5).)
   
   Exploraciones y actividades
9. Exploración de funciones compuestas. Dejar\(A\),\(B\), y\(C\) ser conjuntos no vacíos y dejar\(f: A \to B\) y\(g: B \to C\). Para esta actividad, puede ser útil dibujar tus diagramas de flechas en una disposición triangular de la siguiente manera:
   
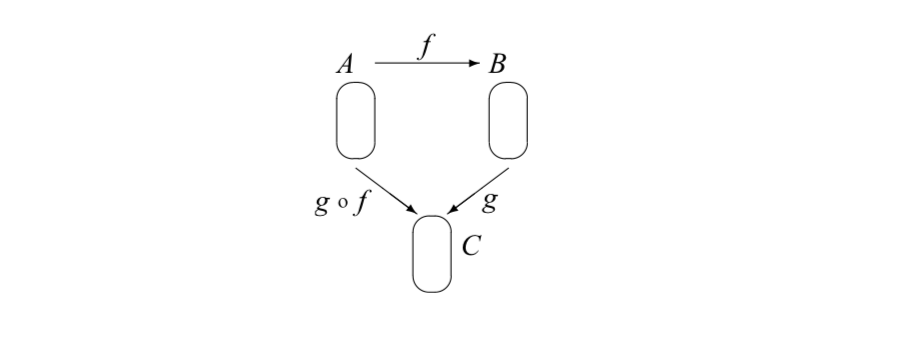
   Podría ser útil considerar ejemplos donde los conjuntos son pequeños. Intente construir ejemplos donde el conjunto\(A\) tenga 2 elementos, el conjunto\(B\) tenga 3 elementos y el conjunto\(C\) tenga 2 elementos.
   
   a) ¿Es posible construir un ejemplo donde\(g \circ f\) es una inyección,\(f\) es una inyección, pero no\(g\) es una inyección? O construir tal ejemplo o explicar por qué no es posible.
   b) ¿Es posible construir un ejemplo donde\(g \circ f\) es una inyección,\(g\) es una inyección, pero no\(f\) es una inyección? O construir tal ejemplo o explicar por qué no es posible.
   c) ¿Es posible construir un ejemplo donde\(g \circ f\) hay una sobreyección,\(f\) es una sobreyección, pero no\(g\) es una sobreyección? O construir tal ejemplo o explicar por qué no es posible.
   d) ¿Es posible construir un ejemplo donde\(g \circ f\) hay una sobreyección,\(g\) es una sobreyección, pero no\(f\) es una sobreyección? O construir tal ejemplo o explicar por qué no es posible.
10. La Prueba del Teorema 6.21. Usa las ideas del Ejercicio (9) para probar el Teorema 6.21. Dejar\(A\),\(B\) y\(C\) ser conjuntos no vacíos y dejar\(f: A \to B\) y\(g: B \to C\).
    
    (a) Si\(g \circ f: A \to C\) es una inyección, entonces\(f: A \to B\) es una inyección.
    (b) Si\(g \circ f: A \to C\) es una sobreyección, entonces\(g: B \to C\) es una sobreyección.
    
    Pista: Para la parte (a), empieza por preguntar: “¿Qué tenemos que hacer para probar que\(f\) es una inyección? ” Comience con una pregunta similar para la parte (b).

Responder

Agrega textos aquí. No elimine primero este texto.