6.5: Funciones inversas

Para esta sección, utilizaremos el concepto de producto cartesiano de dos conjuntos\(A\) y\(B\), denotado por\(A \times B\), que es el conjunto de todos los pares ordenados\((x, y)\) donde\(x \in A\) y\(y \in B\). Es decir,

\(A \times B = \{(x, y)\ |\ x \in A \text{ and } y \in B\}.\)

Consulte la Vista previa de la Actividad\(\PageIndex{2}\) en la Sección 5.4 para una discusión más exhaustiva de este concepto.

PREVIAR ACTIVIDAD\(\PageIndex{1}\): Functions and Sets of Ordered Pairs

Cuando graficamos una función real, trazamos pares ordenados en el plano cartesiano donde la primera coordenada es la entrada de la función y la segunda coordenada es la salida de la función. Por ejemplo, si\(g: \mathbb{R} \to \mathbb{R}\), entonces cada punto en la gráfica de\(g\) es un par ordenado\((x, y)\) de números reales donde\(y = g(x)\). Esto muestra cómo podemos generar pares ordenados a partir de una función. Sucede que podemos hacer esto con cualquier función. Por ejemplo, vamos

\(A = \{1, 2, 3\}\)y\(B = \{a, b\}\).

Definir la función\(F: A \to B\) por

\(F(1) = a\),\(F(2) = b\), y\(F(3) = b\).

Podemos convertir cada uno de estos a un par ordenado en\(A \times B\) usando la entrada como la primera coordenada y la salida como la segunda coordenada. Por ejemplo,\(F(1) = a\) se convierte a\((1, a)\),\(F(2) = b\) se convierte a\((2, b)\), y\(F(3) = b\) se convierte a\((3, b)\). Entonces podemos pensar en esta función como un conjunto de pares ordenados, que es un subconjunto de\(A \times B\), y escribir

\(F = \{(1, a), (2, b), (3, b)\}.\)

Nota: Dado que\(F\) es el nombre de la función, es costumbre usar\(F\) como nombre para el conjunto de pares ordenados.

1. Dejar\(A = \{1, 2, 3\}\) y dejar\(C = \{a, b, c, d\}\). Definir la función\(g: A \to C\) por\(g(1) = a\),\(g(2) = b\), y\(g(3) = d\). Escribe la función\(g\) como un conjunto de pares ordenados en\(A \times C\).

Para otro ejemplo, si tenemos una función real, tal como:\(g: \mathbb{R} \to \mathbb{R}\) by\(g(x) = x^2 - 2\), entonces podemos pensar en\(g\) como el siguiente subconjunto infinito de\(\mathbb{R} \times \mathbb{R}\):

\(g = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ y = x^2 - 2\}.\)

También podemos escribir esto a veces escribir esto como\(g = \{(x, x^2 - 2)\ |\ x \in \mathbb{R}\}.\)

2. \(f: \mathbb{Z} \to \mathbb{Z}\)Déjese definir por\(f(m) = 3m + 5\), para todos\(m \in \mathbb{Z}\). Use la notación set builder para escribir la función\(f\) como un conjunto de pares ordenados y luego use el método roster para escribir la función\(f\) como un conjunto de pares ordenados.

Entonces, cualquier función\(f: A \to B\) puede considerarse como un conjunto de pares ordenados que es un subconjunto de\(A \times B\). Este subconjunto es

\(f = \{(a, f(a))\ |\ a \in A\}\)o\(f = \{(a, b) \in A \times B\ |\ b = f(a)\}.\)

Por otro lado, si empezamos con\(A = \{1, 2, 3\}\),\(B = \{a, b\}\), y

\(G = \{(1, a), (2, a), (3, b)\} \subseteq A \times B,\)

entonces podríamos pensar en\(G\) como una función de\(A\) a\(B\) con\(G(1) = a\)\(G(2) = a\), y\(G(3) = b\). La idea es usar la primera coordenada de cada par ordenado como entrada, y la segunda coordenada como salida. Sin embargo, no todos los subconjuntos de\(A \times B\) pueden usarse para definir una función de\(A\) a\(B\). Esto se explora en las siguientes preguntas.

3. Vamos\(f = \{(1, a), (2, a), (3, a), (1, b)\}\). ¿Podría usarse este conjunto de pares ordenados para definir una función de\(A\) a\(B\)? Explique.
4. Vamos\(g = \{(1, a), (2, a), (3, a)\}\). ¿Podría usarse este conjunto de pares ordenados para definir una función de\(A\) a\(B\)? Explique.
5. Vamos\(h = \{(1, a), (2, b)\}\). ¿Podría usarse este conjunto de pares ordenados para definir una función de\(A\) a\(B\)? Explique.

PREVIAR ACTIVIDAD\(\PageIndex{1}\): A Composition of Two Specific Functions

Dejar\(A = \{a, b, c, d\}\) y dejar\(B = \{p, q, r, s\}\).

1. Construir un ejemplo de una función\(f: A \to B\) que sea una biyección. Dibuja un diagrama de flechas para esta función.
2. En tu diagrama de flechas, dibuja una flecha desde cada elemento de\(B\) atrás hasta su elemento correspondiente en\(A\). Explique por qué esto define una función de\(B\) a\(A\).
3. Si el nombre de la función en la Parte (2) es\(g\), así que\(g: B \to A\), ¿qué son\(g(p)\),\(g(q)\),\(g(r)\), y\(g(s)\)?
4. Construir una tabla de valores para cada una de las funciones\(g \circ f: A \to A\) y\(f \circ g: B \to B\). ¿Qué observas de estas tablas de valores?

La representación de pares ordenados de una función

En Preview Activity\(\PageIndex{1}\), observamos que si tenemos una función\(f: A \to B\), podemos generar un conjunto de pares ordenados\(f\) que es un subconjunto de la\(A \times B\) siguiente manera:

\(f = \{(a, f(a)\ |\ a \in A\}\)o\(f = \{(a, b) \in A \times B\ |\ b = f(a)\}.\)

Sin embargo, también aprendimos que algunos conjuntos de pares ordenados no se pueden usar para definir una función. Ahora queremos explorar bajo qué condiciones se puede usar un conjunto de pares ordenados para definir una función. Comenzando con una función\(f: A \to B\), ya que dom (\(f\)) =\(A\), sabemos que

\[\text{For every } a \in A \text{, there exists a } b \in B \text{ such that } (a, b) \in f. \label{6.5.1}\]

Específicamente, utilizamos\(b = f(a)\). Esto dice que cada elemento de\(A\) puede ser utilizado como entrada. Además, para ser una función, cada entrada puede producir solo una salida. En cuanto a pares ordenados, esto significa que nunca habrá dos pares ordenados\((a, b)\) y\((a, c)\) en la función\(f\) donde\(a \in A\),\(b, c \in B\), y\(b \ne c\). Podemos formular esto como una declaración condicional de la siguiente manera:

\[\text{For every } a \in A \text{ and every } b, c \in B, \\ \text{if } (a, b) \in f \text{ and } (a,c) \in f \text{, then } b = c. \label{6.5.2}\]

Esto también significa que si comenzamos con un subconjunto\(f\) de\(A \times B\) que satisface las condiciones en la Ecuación\ ref {6.5.1} y\ ref {6.5.2}, entonces podemos considerar\(f\) que es una función de\(A\) a\(B\) usando\(b = f(a)\) siempre que\((a, b)\) esté en\(f\). Esto prueba el siguiente teorema.

Teorema 6.22

Let\(A\) y\(B\) be conjuntos no vacíos y let\(f\) ser un subconjunto de\(A \times B\) que satisfaga las siguientes dos propiedades:

• Por cada\(a \in A\), existe\(b \in B\) tal que\((a, b) \in f\); y
• Por todos\(a \in A\) y cada uno\(b, c \in B\), si\((a, b) \in f\) y\((a, c) \in f\), entonces\(b = c\).

Si usamos\(f(a) = b\) siempre\((a, b) \in f\), entonces\(f\) es una función de\(A\) a\(B\).

Una Nota sobre el Teorema 6.22. La primera condición en el Teorema 6.22 significa que cada elemento de A es una entrada, y la segunda condición asegura que cada entrada tenga exactamente una salida. Muchos textos utilizarán Teorema 6.22 como definición de una función. Muchos matemáticos creen que esta representación ordenada por pares de una función es la definición más rigurosa de una función. Nos permite utilizar la teoría de conjuntos para trabajar y comparar funciones. Por ejemplo, la igualdad de funciones se convierte en cuestión de igualdad de conjuntos. Por lo tanto, muchos libros de texto utilizarán la representación de pares ordenados de una función como definición de una función.

Comprobación de progreso 6.23 (conjuntos de pares ordenados que no son funciones)

Dejar\(A = \{1, 2, 3\}\) y dejar\(B = \{a, b\}\). Explique por qué cada uno de los siguientes subconjuntos de\(A \times B\) no se puede utilizar para definir una función de\(A\) a\(B\).

1. \(F = \{(1, a), (2, a)\}\),
2. \(G = \{(1, a), (2, b), (3, c), (2, c)\}\).

Contestar

Agrega textos aquí. No borre primero este texto.

La inversa de una función

En cursos previos de matemáticas aprendimos que la función exponencial (con base\(e\)) y las funciones de logaritmo natural son inversas unas de otras. Esto se expresó a menudo de la siguiente manera:

Para cada uno\(x \in R\) con\(x > 0\) y para cada uno\(y \in \mathbb{R}\),\(y = \text{ln}x\) si y solo si\(x = e^y\).

Observe que esto significa que\(x\) es la entrada y\(y\) es la salida para la función de logaritmo natural si y solo si\(y\) es la entrada y\(x\) es la salida para la función exponencial. En esencia, la función inversa (en este caso, la función exponencial) invierte la acción de la función original (en este caso, la función logaritmo natural). En términos de pares ordenados (pares entrada-salida), esto significa que si\((x, y)\) es un par ordenado para una función, entonces\((y, x)\) es un par ordenado para su inverso. Esta idea de revertir los roles de la primera y segunda coordenadas es la base de nuestra definición de la inversa de una función.

Definición: Inverso de una función

Dejar\(f: A \to B\) ser una función. El inverso de\(f\), denotado por\(f^{-1}\), es el conjunto de pares ordenados\(\{(b, a) \in B \times A\ |\ f(a) = b\}\). Es decir,

\(f^{-1} = \{(b, a) \in B \times A\ |\ f(a) = b\}\).

Si usamos la representación de par ordenada para\(f\), también podríamos escribir

\(f^{-1} = \{(b, a) \in B \times A\ |\ (a, b) \in f\}\).

Observe que esta definición no establece que\(f^{-1}\) sea una función. Es simplemente un subconjunto de\(B \times A\). Después de estudiar el material en el Capítulo 7, diremos que esto significa que\(f^{-1}\) es una relación de\(B\) a\(A\). Este hecho, sin embargo, no es importante para nosotros ahora. Nos interesa principalmente la siguiente pregunta:

¿Bajo qué condiciones la inversa de la función\(f: A \to B\) será una función de\(B\) a\(A\)?

Comprobación de progreso 6.24: Explorando la inversa de una función

Vamos\(A = \{a, b, c\}\),\(B = \{a, b, c, d\}\), y\(C = \{p, q, r\}\). Definir

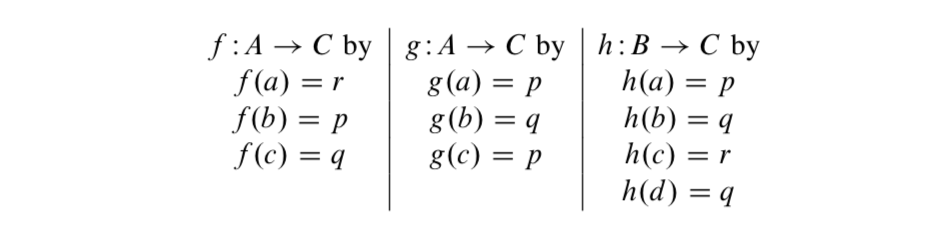
1. Dibuja un diagrama de flechas para cada función.
2. Determinar la inversa de cada función como un conjunto de pares ordenados.
3. (a) ¿Es\(f^{-1}\) una función de\(C\) a\(A\)? Explique.
   b) ¿Es\(g^{-1}\) una función de\(C\) a\(A\)? Explique.
   c) ¿Es\(h^{-1}\) una función de\(C\) a\(B\)? Explique.
4. Dibuja un diagrama de flechas para cada inverso de la Parte (3) que es una función. Utilice su diagrama de flechas existente de la Parte (1) para dibujar este diagrama de flechas.
5. Hacer una conjetura sobre qué condiciones en una función\(F: S \to T\) asegurará que su inversa sea una función de\(T\) a\(S\).

Contestar

Agrega textos aquí. No borre primero este texto.

Consideraremos ahora un argumento general sugerido por las exploraciones en Avance Check 6.24. Por definición, si\(f: A \to B\) es una función, entonces\(f^{-1}\) es un subconjunto de\(B \times A\). Sin embargo,\(f^{-1}\) puede o no ser una función de\(B\) a\(A\). Por ejemplo, supongamos que\(s, t \in A\) con\(s \ne t\) y\(f(s) = f(t)\). Esto se representa en la Figura 6.9.

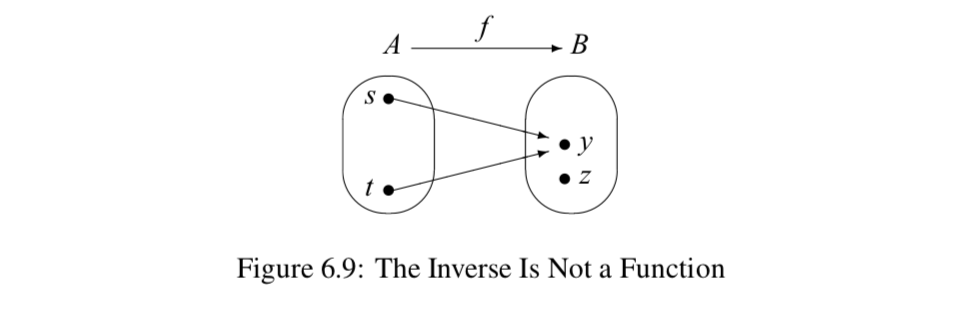
En este caso, si tratamos de revertir las flechas, no obtendremos una función de\(B\) a\(A\). Esto es porque\((y, s) \in f^{-1}\) y\((y, t) \in f^{-1}\) con\(s \ne t\). En consecuencia, no\(f^{-1}\) es una función. Esto sugiere que cuando no\(f\) es una inyección, entonces no\(f^{-1}\) es una función.

También, si no\(f\) es una sobreyección, entonces existe\(z \in B\) tal que\(f(a) \ne z\) para todos\(a \in A\), como en el diagrama de la Figura 6.9. En otras palabras, no hay par ordenado en\(f\) con\(z\) como segunda coordenada. Esto significa que no habría un par ordenado en\(f^{-1}\) con\(z\) como primera coordenada. En consecuencia,\(f^{-1}\) no puede ser una función de\(B\) a\(A\).

Esto motiva la afirmación en el Teorema 6.25. En la prueba de este teorema, frecuentemente cambiaremos de ida y vuelta de la representación entrada-salida de una función y la representación de pares ordenados de una función. La idea es que si\(G: S \to T\) es una función, entonces para\(s \in S\) y\(t \in T\),

\(G(s) = t\)si y sólo si\((s, t) \in G\).

Cuando usamos la representación de par ordenado de una función, también usaremos la representación de par ordenado de su inversa. En este caso, sabemos que

\((s, t) \in G\)si y sólo si\((t, s) \in G^{-1}\).

Teorema 6.25.

Dejar\(A\) y\(B\) ser conjuntos no vacíos y dejar\(f: A \to B\). El inverso de\(f\) es una función de\(B\) a\(A\) si y solo si\(f\) es una biyección.

Prueba

Dejar\(A\) y\(B\) ser conjuntos no vacíos y dejar\(f: A \to B\). Primero asumiremos que f es una bijección y probaremos que\(f^{-1}\) es una función de\(B\) a\(A\). Para ello, mostraremos que\(f^{-1}\) satisface las dos condiciones del Teorema 6.22.

Primero elegimos\(b \in B\). Dado que la función\(f\) es una suryección, existe\(a \in A\) tal que\(f(a) = b\). Esto implica eso\((a, b) \in f\) y por lo tanto eso\((b, a) \in f^{-1}\). Así, cada elemento de\(B\) es la primera coordenada de un par ordenado en\(f^{-1}\), y por lo tanto\(f^{-1}\) satisface la primera condición del Teorema 6.22.

Para probar que\(f^{-1}\) satisface la segunda condición del Teorema 6.22, debemos demostrar que cada elemento de\(B\) es la primera coordenada de exactamente un par ordenado en\(f^{-1}\). Así que vamos\(b \in B\),\(a_1, a_2 \in A\) y supongamos que

\((b, a_1) \in f^{-1}\)y\((b, a_2) \in f^{-1}\).

Esto significa que\ ((a_1, b)\ in f) y\ ((a_2, b)\ in f). Entonces podemos concluir que

\(f(a_1) = b\)y\(f(a_2) = b\).

Pero esto significa eso\(f(a_1) = f(a_2)\). Ya que\(f\) es una biyección, es una inyección, y podemos concluir que\(a_1 = a_2\). Esto demuestra que\(b\) es el primer elemento de un solo par ordenado en\(f^{-1}\). En consecuencia, hemos demostrado que\(f^{-1}\) satisface ambas condiciones del Teorema 6.22 y de ahí que\(f^{-1}\) sea una función de\(B\) a\(A\).

Ahora asumimos que\(f^{-1}\) es una función\(B\) para\(A\) y demostrar que\(f\) es una biyección. Primero, para probar que\(f\) es una inyección, asumimos eso\(a_1, a_2 \in A\) y aquello\(f(a_1) = f(a_2)\). Eso queremos demostrarlo\(a_1 = a_2\). Si lo permitimos\(b = f(a_1) = f(a_2)\), podemos concluir que

\ ((a_1, b)\ en f) y\ ((a_2, b)\ en f).

Pero esto significa que

\((b, a_1) \in f^{-1}\)y\((b, a_2) \in f^{-1}\).

Ya que hemos asumido que\(f^{-1}\) es una función, podemos concluir que\(a_1 = a_2\). De ahí que f sea una inyección.

Ahora para probar que\(f\) es una surjección, elegimos\(b \in B\) y demostraremos que existe\(a \in A\) tal eso\(f(a) = b\). Ya que\(f^{-1}\) es una función,\(b\) debe ser la primera coordenada de algún par ordenado en\(f^{-1}\). En consecuencia, existe\(a \in A\) tal que

\((b, a) \in. f^{-1}\).

Ahora esto implica eso\((a, b) \in f\) y de ahí eso\(f(a) = b\). Esto prueba que\(f\) es una sobrejección. Como también hemos demostrado que\(f\) es una inyección, concluimos que\(f\) es una biyección.

Notación de función inversa

En la situación donde\(f: A \to B\) es una biyección y\(f^{-1}\) es una función de\(B\) a\(A\), podemos escribir\(f^{-1}: B \to A\). En este caso, con frecuencia decimos que\(f\) es una función invertible, y generalmente no usamos la representación de pares ordenados para ninguno\(f\) o\(f^{-1}\). En lugar de escribir\((a, b) \in f\), escribimos\(f(a) = b\), y en lugar de escribir\((b, a) \in. f^{-1}\), escribimos\(f^{-1}(b) = a\). Usando el hecho de que\((a, b) \in f\) si y solo si\((b, a) \in. f^{-1}\), ahora podemos escribir\(f(a) = b\) si y solo si\(f^{-1}(b) = a\). Resumimos esto en el Teorema 6.26.

Teorema 6.26

Dejar\(A\) y\(B\) ser conjuntos no vacíos y dejar\(f: A \to B\) que sea una bijección. Entonces\(f^{-1}: B \to A\) es una función, y para cada\(a \in A\) y\(b \in B\).

\(f(a) = b\)si y sólo si\(f^{-1}(b) = a\).

Ejemplo 6.27: Notación de funciones inversas

Para un ejemplo del uso de la notación en Teorema 6.26, let\(\mathbb{R}^{+} = \{x \in \mathbb{R}\ |\ x>0\}\). Definir

\(f: \mathbb{R} \to \mathbb{R}\)por\(f(x) = x^3\); y\(g: \mathbb{R} \to \mathbb{R}^{+}\) por\(g(x) = e^x\).

Observe que\(\mathbb{R}^{+}\) es el codominio de\(g\). Entonces podemos decir que ambas\(f\) y\(g\) son bijecciones. En consecuencia, las inversas de estas funciones también son funciones. De hecho,

\(f^{-1}: \mathbb{R} \to \mathbb{R}\)por\(f^{-1}(y) = \sqrt[3] {y}\); y\(g^{-1}: \mathbb{R}^{+} \to \mathbb{R}\) por\(g^{-1}(y) = \text{In}y\).

Para cada función (y su inversa), podemos escribir el resultado del Teorema 6.26 de la siguiente manera:

Teoremas sobre las funciones inversas

Los siguientes dos resultados en esta sección son dos teoremas importantes sobre las funciones inversas. El primero es en realidad un corolario del Teorema 6.26.

Corolario 6.28.

Dejar\(A\) y\(B\) ser conjuntos no vacíos y dejar que\(f: A \to B\) sea una bijección. Entonces

1. Para cada\(x\) en\(A\),\((f^{-1} \circ f)(x) = x\)).
2. Para cada\(y\) en\(B\),\((f \circ f^{-1})(y) = y\)).

Prueba

Dejar\(A\) y\(B\) ser conjuntos no vacíos y asumir que\(f: A \to B\) es una bijección. Así que vamos\(x \in A\) y vamos\(f(x) = y\). Por Teorema 6.26, podemos concluir que\(f^{-1}(y) = x\). Por lo tanto,

\[\begin{array} {rcl} {(f^{-1} \circ f)(x)} &= & {f^{-1}(f(x))} \\ {} &= & {f^{-1}(y}} \\ {} &= & {x.} \end{array}\]

De ahí, para cada uno\(x \in A\),\((f^{-1} \circ f)(x) = x\)).

El comprobante que para cada uno\(y\) en\(B\),\((f \circ f^{-1})(y) = y\)) es Ejercicio (4).

Ejemplo 6.27 (continuación)

Para la función de cubo y la función de raíz cúbica, hemos visto que

Para\(x, y \in \mathbb{R}\),\(x^3 = y\) si y solo si\(\sqrt[3]{y} = x\).

Observe que

• Si sustituimos\(x^3 = y\) en la ecuación\(\sqrt[3]{y} = x\), obtenemos\(\sqrt[3]{x^3} = x\).
• Si sustituimos\(\sqrt[3]{y} = x\) en la ecuación\(x^3 = y\), obtenemos\((\sqrt[3]{y})^3 = y\).

Esta es una ilustración de Corolario 6.28. Podemos ver esto usando\(f: \mathbb{R} \to \mathbb{R}\) definido por\(f(x) = x^3\) y\(f^{-1}: \mathbb{R} \to \mathbb{R}\) definido por\(f^{-1}(y) = \sqrt[3]{y}\). Entonces\(f^{-1} \circ f: \mathbb{R} \to \mathbb{R}\) y\(f^{-1} \circ f = I_{\mathbb{R}}\),

\[\beign{array} {rcl} [(f^{-1} \circ f)(x)} &= & {x} \\ {f^{-1}(f(x))} &= & {x} \\ {f^{-1}(x^3)} &= & {x} \\ {\sqrt[3]{x^3}} &= & {x.} \end{array}\]

De igual manera, la ecuación\((\sqrt[3]{y})^3 = y\) para cada uno se\(y \in \mathbb{R}\) puede obtener del hecho de que para cada uno\(y \in \mathbb{R}\),\((f \circ f^{-1})(y) = y\)).

Ahora vamos a considerar el caso donde\(f: A \to B\) y\(g: B \to C\) son ambas bijecciones. En este caso,\(f^{-1}: B \to A\) y\(g^{-1}: C \to B\). La Figura 6.10 puede ser utilizada para ilustrar esta situación.

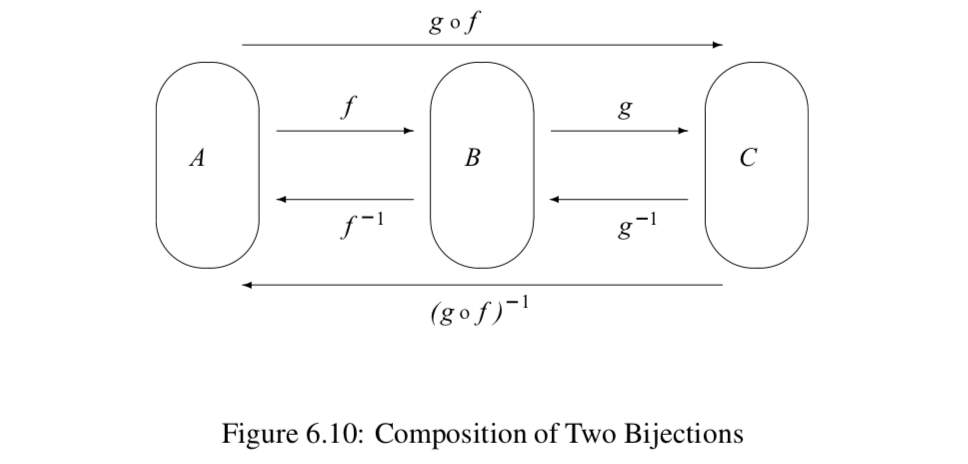
Por Teorema 6.20,\(g \circ f: A \to C\) es también una biyección. De ahí que, por el Teorema 6.25,\((g \circ f)^{-1}\) sea una función y, de hecho,\((g \circ f)^{-1}: C \to A\). Observe que también podemos formar la composición de\(g^{-1}\) seguido por\(f^{-1}\) para obtener\(f^{-1} \circ g^{-1}: C \to A\). La Figura 6.10 ayuda a ilustrar el resultado del siguiente teorema.

Teorema 6.29.

Dejar\(f: A \to B\) y\(g: B \to C\) ser bijecciones. Entonces\(g \circ f\) es una biyección y\((g \circ f)^{-1} = f^{-1} \circ g^{-1}\).

Prueba

Dejar\(f: A \to B\) y\(g: B \to C\) ser bijecciones. Entonces\(f^{-1}: B \to A\) y\(g^{-1}: C \to B\). De ahí,\(f^{-1} \circ g^{-1}: C \to A\). También, por Teorema 6.20,\(g \circ f: A \to C\) es una biyección, y por lo tanto\((g \circ f)^{-1}: C \to A\). Ahora vamos a demostrar eso para cada uno\(z \in C\),\((g \circ f)^{-1}(z) = f^{-1} \circ g^{-1}(z)\).

Vamos\(z \in C\). Dado que la función\(g\) es una sobreyección, existe\(y \in B\) tal que

\[g(y) = z.\]

También, como\(f\) es una sobrejección, existe\(x \in A\) tal que

\[f(x) = y.\]

Ahora bien, estas dos ecuaciones se pueden escribir en términos de las respectivas funciones inversas como

\[g^{-1}(z) = y\text[; and}\]

\[f^{-1}(y) = x.\]

Usando las ecuaciones (6.5.5) y (6.5.6), vemos que

\[\begin{array} {rcl} {f^{-1} \circ g^{-1}(z)} &= & {f^{-1}(g^{-1}(z))} \\ {} &= & {f^{-1}(y)} \\ {} &= &{x.} \end{array}\]

Usando de nuevo las ecuaciones (6.5.3) y (6.5.4), vemos eso\((g \circ f)(x) = z\). Sin embargo, en términos de la función inversa, esto significa que

\[(g \circ f)^{-1}(z) = x.\]

Comparando las ecuaciones (6.5.7) y (6.5.8), hemos demostrado que para todos\(z \in C\),\((g \circ f)^{-1}(z) = f^{-1} \circ g^{-1}(z)\). Esto lo demuestra\((g \circ f)^{-1} = f^{-1} \circ g^{-1}\).

Ejercicio 6.5

1. Dejar\(A = \{1, 2, 3\}\) y\(B = \{a, b, c\}\).
   (a) Construir un ejemplo de una función\(f: A \to B\) que no sea una biyección. Escribe la inversa de esta función como un conjunto de pares ordenados. ¿Es la inversa de\(f\) una función? Explique. Si es así, dibuje un diagrama de flechas para\(f\) y\(f^{-1}\).
   (b) Construir un ejemplo de una función\(g: A \to B\) que sea una biyección. Escribe la inversa de esta función como un conjunto de pares ordenados. ¿Es la inversa de\(g\) una función? Explique. Si es así, dibuje un diagrama de flechas para\(g\) y\(g^{-1}\).
2. Vamos\(S = \{a, b, c, d\}\). \(f\)Definir\(f: S \to S\) definiendo ser el siguiente conjunto de pares ordenados.
   \[f = \{(a, c), (b, b), (c, d), (d, a)\}\]
   (a) Dibuje un diagrama de flechas para representar la función\(f\). ¿Es la función fa bijección?
   (b) Escribir la inversa de\(f\) como un conjunto de pares ordenados. ¿Es\(f^{-1}\) una función? Explique.
   (c) Dibuja un diagrama de flechas para\(f^{-1}\) usar el diagrama de flechas del Ejercicio (2a).
   (d) Cómputos\((f^{-1} \circ f)(x)\) y\((f \circ f^{-1}(x)\) para cada uno\(x\) en\(S\). ¿Qué teorema ilustra esto?
3. Las funciones inversas se pueden utilizar para ayudar a resolver ciertas ecuaciones. La idea es usar una función inversa para deshacer la función.
   (a) Dado que la función de raíz cúbica y la función de cubo son inversas entre sí, a menudo podemos usar la función de raíz cúbica para ayudar a resolver una ecuación que involucra un cubo. Por ejemplo, el paso principal para resolver la ecuación
   \[(2t - 1)^3 = 20\]
   es tomar la raíz cúbica de cada lado de la ecuación. Esto da
   \[\begin{array} {rcl} {\sqrt[3]{(2t - 1)^3} &= & {\sqrt[3]{20}} \\ {2t - 1} &= &{\sqrt[3]{20}.} \end{array}\]
   Explicar cómo este paso en la resolución de la ecuación es un uso de Corolario 6.28.
   
   (b) Un paso principal para resolver la ecuación\ (e^ {2t - 1} = 20} es tomar el logaritmo natural de ambos lados de esta ecuación. Explicar cómo este paso es un uso de Corolario 6.28, y luego resolver la ecuación resultante para obtener una solución para t en términos de la función logaritmo natural.
   c) ¿Cómo son similares los métodos de resolución de las ecuaciones en el Ejercicio (3a) y en el Ejercicio (3b)?
4. Demostrar Parte (2) del Corolario 6.28. Dejar\(A\) y\(B\) ser conjuntos no vacíos y dejar que\(f: A \to B\) sea una bijección. Entonces para cada\(y\) en\(B\),\((f \circ f^{-1} (y) = y\).
5. En la comprobación de progreso 6.6 en la página 298, definimos la función de identidad en un conjunto. La función de identidad en el conjunto\(T\), denotada por\(I_T\), es la función\(I_T: T \to T\) definida por\(I_T(t) = t\) para cada\(t\) entrada\(T\). Explicar cómo se puede afirmar el Corolario 6.28 utilizando el concepto de igualdad de funciones y las funciones de identidad en los conjuntos\(A\) y\(B\).
6. Dejar\(f: A \to B\) y\(g: B \to A\). Dejar\(I_A\) y\(I_B\) ser las funciones de identidad en los conjuntos\(A\) y\(B\), respectivamente. Demostrar cada uno de los siguientes: a
   ) Si\(g \circ f = I_A\), entonces\(f\) es una inyección.
   (b) Si\(g \circ g = I_B\), entonces\(f\) es una sobrejección.
   (c) Si\(g \circ f = I_A\) y\(g \circ g = I_B\), entonces\(f\) y\(g\) son biyecciones y\(g = f^{-1}\).
7. a) Definir\(f: \mathbb{R} \to \mathbb{R}\) por\(f(x) = e^{-x^2}\). ¿Es la inversa de\(f\) una función? Justifica tu conclusión.
   b) Dejar\(\mathbb{R}^{\ast} = \{x \in \mathbb{R}\ |\ x \ge 0\}\). Definir\(g: \mathbb{R}^{\ast} \to (0,1]\) por\(g(x) = e^{-x^2}\). ¿Es la inversa de\(g\) una función? Justifica tu conclusión.
8. (a) Que\(f: \mathbb{R} \to \mathbb{R}\) se defina por\(f(x) = x^2\). Explique por qué la inversa de no\(f\) es una función.
   b) Dejar\(\mathbb{R}^{\ast} = \{t \in \mathbb{R}\ |\ t \ge 0\}\). Definir\(g: \mathbb{R}^{\ast} \to \mathbb{R}^{\ast}\) por\(g(x) = x^2\). Explique por qué esta función de cuadratura (con un dominio restringido y un codominio) es una biyección.
   (c) Explicar cómo definir la función raíz cuadrada como la inversa de la función en el Ejercicio (8b).
   d) Verdadero o falso:\((\sqrt{x})^2 = x\) para todos\(x \in \mathbb{R}\) tales que\(x \ge 0\).
   e) Verdadero o falso:\(\sqrt{x^2} = x\) para todos\(x \in \mathbb{R}\).
9. Demostrar lo siguiente:
   Si\(f: A \to B\) es una biyección, entonces también\(f^{-1}: B \to A\) es una biyección.
10. Para cada número natural\(k\), deja\(A_k\) ser un conjunto, y para cada número natural\(n\), deja\(f_n: A_n \to A_{n + 1}\).
    Por ejemplo,\(f_1 = A_1 \to A_2\),\(f_1 = A_1 \to A_2\),\(f_2 = A_2 \to A_3\),\(f_3 = A_3 \to A_4\), y así sucesivamente.
    Usa inducción matemática para demostrar que para cada número natural\(n\) con\(n \ge 2\), si\(f_1\)\(f_2\),,...,\(f_n\) son todas biyecciones, entonces\(f_n \circ f_{n - 1} \circ \cdot\cdot\cdot \circ f_2 \circ f_1\) es una biyección y
    \ [(f_n\ circ f_ {n - 1}\ circ\ cdot\ cdot\ cdot\ circ f_2\ circ f_1) ^ {-1} = f_ {1} ^ {-1}\ cdot f_ {2} ^ {-1}\ cdot\ cdot\ cdot\ cdot\ cdot\ circ f_ {n - 1} ^ {-1}\ circ f_ {n} ^ {-1}
    Nota: Esta es una extensión del Teorema 6.29. De hecho, el Teorema 6.29 es el paso base de esta prueba para\(n = 2\).
11. \(a) Define \(f: \mathbb{R} \to \mathbb{R}\)por\(f(x) = x^2 - 4\) para todos\(x \in \mathbb{R}\). Explique por qué la inversa de la función no\(f\) es una función.
    b) Dejar\(\mathbb{R}^{\ast} = \{x \in \mathbb{R}\ |\ x \ge 0\}\) y dejar\(T = \{y \in \mathbb{R}\ |\ y \ge -4\}\). Definir\(F: \mathbb{R}^{\ast} \to T\) por\(F(x) = x^2 - 4\) para todos\(x \in \mathbb{R}^{\ast}\). Explicar por qué la inversa de la función\(F\) es una función y encontrar una fórmula para\(F^{-1}(y)\), dónde\(y \in T\).
12. Vamos\(\mathbb{Z}_5 = \{0, 1, 2, 3, 4\}\).
    (a) Definir\(f: \mathbb{Z}_5 \to \mathbb{Z}_5\) por\(f(x) = x^2 + 4\) (mod 5) para todos\(x \in \mathbb{Z}_5\). Escribe la inversa de\(f\) como un conjunto de pares ordenados y explica por qué no\(f^{-1}\) es una función.
    (b) Definir\(g: \mathbb{Z}_5 \to \mathbb{Z}_5\) por\(g(x) = x^3 + 4\) (mod 5) para todos\(x \in \mathbb{Z}_5\). Escribe la inversa de\(g\) como un conjunto de pares ordenados y explica por qué no\(g^{-1}\) es una función.
    c) ¿Es posible escribir una fórmula para\(g^{-1}(y)\), dónde\(y \in \mathbb{Z}_5\)? La respuesta a esta pregunta depende de si es posible o no definir una raíz cubo de elementos de\(\mathbb{Z}_5\). Recordemos que para un número real\(x\), definimos la raíz cubo de x al número real\(y\) tal que\(y^3 = x\). Es decir,
    \[y = \sqrt[3]{x} \text{ if and only if } y^3 = x.\]
    Usando esta idea, ¿es posible definir la raíz cubo de cada número en\(\mathbb{Z}_5\)? Si es así, qué es\(\sqrt[3]{0}\)\(\sqrt[3]{1}\),\(\sqrt[3]{2}\),\(\sqrt[3]{3}\), y\(\sqrt[3]{4}\).
    (d) Ahora responde a la ecuestión planteada al inicio de la Parte (c). Si es posible, determine una fórmula para\(g^{-1}(y)\) dónde\(g^{-1}: \mathbb{Z}_5 \to \mathbb{Z}_5\).
    
    Exploraciones y actividades
13. Construyendo una Función Inversa. Si\(f: A \to B\) es una biyección, entonces sabemos que su inversa es una función. Si se nos da una fórmula para la función\(f\), puede ser deseable determinar una fórmula para la función\(f^{-1}\). Esto a veces se puede hacer, mientras que en otras ocasiones es muy difícil o incluso imposible.
    Dejar\(f: \mathbb{R} \to \mathbb{R}\) ser definido por\(f(x) = 2x^3 - 7\). Una gráfica de esta función sugeriría que esta función es una biyección.
    
    a) Demostrar que la función f es una inyección y una sobreyección.
    
    Vamos\(y \in \mathbb{R}\). Una forma de demostrar que\(f\) es una surjección es establecer\(y = f(x)\) y resolver para\(x\). Si esto se puede hacer, entonces sabríamos que existe\(x \in \mathbb{R}\) tal eso\(f(x) = y\). Para la función\(f\), estamos usando\(x\) para la entrada e y para la salida. Al resolver for\(x\) en términos de\(y\), estamos intentando escribir una fórmula donde\(y\) está la entrada y\(x\) es la salida. Esta fórmula representa la función inversa.
    
    (b) Resolver la ecuación\(y = 2x^3 - 7\) para\(x\). Usa esto para escribir una fórmula para\(f^{-1}(y)\), donde\(f^{-1}: \mathbb{R} \to \mathbb{R}\).
    (c) Utilizar el resultado de la Parte (13b) para verificar que para cada uno\(x \in \mathbb{R}\),\(f^{-1}(f(x)) = x\) y para cada uno\(y \in \mathbb{R}\),\(f(f^{-1}(y)) = y\).
    
    Ahora vamos\(\mathbb{R}^{+} = \{y \in \mathbb{R}\ |\ y > 0\}\). Definir\(g: \mathbb{R} \to \mathbb{R}^{+}\) por\(g(x) = e^{2x - 1}\).
    
    d) Establecer\(y = e^{2x - 1}\) y resolver\(x\) en términos de\(y\).
    (e) Utilice su trabajo en Ejercicio (13d) para definir una función\(h: \mathbb{R}^{+} \to \mathbb{R}\).
    f) Para cada uno\(x \in \mathbb{R}\), determinar\((h \circ g)(x)\) y para cada uno\(y \in \mathbb{R}^{+}\), determinar\((g \circ h)(y)\).
    g) Utilizar el Ejercicio (6) para explicar por qué\(h = g^{-1}\).
14. La Función Sinusoidal Inversa. Hemos visto que para obtener una función inversa, a veces es necesario restringir el dominio (o el codominio) de una función.
    
    (a) Que\(f: \mathbb{R} \to \mathbb{R}\) se defina por\(f(x) = sin x\). Explique por qué la inversa de la función no\(f\) es una función. (Un gráfico puede ser útil.)
    
    Observe que si usamos la representación de par ordenado, entonces la función seno se puede representar como
    \[f = \{(x, y) \in \mathbb{R} \to \mathbb{R}\ |\ y = sin x\}.\]
    Si denotamos la inversa de la función sinusoidal por pecado\(^{-1}\), entonces
    \[f^{-1} = \{(y, x) \in \mathbb{R} \to \mathbb{R}\ |\ y = sin x\}.\]
    
    La parte (14a) prueba que no\(f^{-1}\) es una función. Sin embargo, en cursos previos de matemáticas, frecuentemente se utilizó la “función sinusoidal inversa”. Esta no es realmente la inversa de la función sinusoidal tal como se define en la Parte (14a) sino, más bien, es la inversa de la función sinusoidal restringida al dominio\([-\dfrac{\pi}{2}, \dfrac{\pi}{2}]\).
    
    b) Explicar por qué la función\(F: [-\dfrac{\pi}{2}, \dfrac{\pi}{2}] \to [-1, 1]\) definida por\(F(x) = sin x\) es una biyección.
    
    La inversa de la función en Part (14b) es en sí misma una función y se llama la función sinusoidal inversa (o a veces la función arcoseno).
    
    (c) ¿Cuál es el dominio de la función sinusoidal inversa? ¿Cuáles son el rango y el codominio de la función sinusoidal inversa?
    
    Ahora usemos\(F(x) = \text{sin(\(x\))}\) para representar la función sinusoidal restringida en la Parte (14b). Por lo tanto,\(F^{-1} (x) = \text{sin\(^{-1}\) (\(x\))}\) se puede utilizar para representar la función sinusoidal inversa. Observe que
    \[F: [-\dfrac{\pi}{2}, \dfrac{\pi}{2}] \to [-1, 1] \text{ and } F^{-1}: [-1, 1] \to [-\dfrac{\pi}{2}, \dfrac{\pi}{2}].\]
    (d) Usando esta notación, explique por qué
    \(\text{sin\(^{-1}\)} y = x\) si y solo si [\(y = \text{sin \(x\)}\) y\(-\dfrac{\pi}{2} \le x \le \dfrac{\pi}{2}\)];
    \(\text{sin(sin\(^{-1}\)} (y)) = y\) para todos\(y \in [-1, 1]\); y
    \(\text{sin\(^{-1}\) (sin ( \(x\)))} = x\) para todos\(x \in [-\dfrac{\pi}{2}, \dfrac{\pi}{2}].\)

Contestar

Agrega textos aquí. No borre primero este texto.