7.1: Relaciones

PREVIAR ACTIVIDAD\(\PageIndex{1}\): The United States of America

Recordemos de la Sección 5.4 que el producto cartesiano de dos juegos\(A\) y\(B\), escrito\(A \times B\), es el conjunto de todos los pares ordenados\((a, b)\), donde\(a \in A\) y\(b \in B\). Es decir,\(A \times B = \{(a, b)\ |\ a \in A \text{ and } b \in B\}\).

Que\(A\) sea el conjunto de todos los estados en Estados Unidos y que

\(R = \{(x, y) \in A \times A\ |\ x \text{ and } y \text{ have a land border in common}\}\).

Por ejemplo, dado que California y Oregón tienen una frontera terrestre, podemos decir eso (California, Oregón)\(\in R\) y (Oregón, California)\(\in R\). También, dado que California y Michigan no comparten frontera terrestre, (California, Michigan)\(\notin R\) y (Michigan, California)\(\notin R\).

1. Utilice el método roster para especificar los elementos en cada uno de los siguientes conjuntos:
   
   (a)\(B = \{y \in A\ |\ (\text{Michigan}, y) \in R\}\)
   (b)\(C = \{x \in A\ |\ (x, \text{Michigan}) \in R\}\)
   (c)\(D = \{y \in A\ |\ (\text{Wisconsin}, y) \in R\}\)
2. Encuentra dos ejemplos diferentes de dos pares ordenados\((x, y)\) y\((y, z)\) tal que\((x, y) \in R\),\((y, z) \in R\), pero\((x, z) \notin R\), o explicar por qué no existe tal ejemplo. En base a esto, ¿es verdadera o falsa la siguiente declaración condicional?
   
   Para todos\(x, y, z \in A\), si\((x, y) \in R\) y\((y, z) \in R\), entonces\((x, z) \in R\).
3. ¿La siguiente declaración condicional es verdadera o falsa? Explique.
   
   Para todos\(x, y \in A\), si\((x, y) \in R\) entonces\((y, x) \in R\).

PREVIAR ACTIVIDAD\(\PageIndex{2}\): The Solution Set of an Equation with Two Variables

En la Sección 2.3, se introdujo el concepto del conjunto de verdad de una oración abierta con una variable. Esto se definió como el conjunto de todos los elementos del conjunto universal que pueden ser sustituidos por la variable para hacer de la oración abierta una verdadera proposición. Asumir eso\(x\) y\(y\) representar números reales. Luego la ecuación

\(4x^2 + y^2 = 16\)

es una oración abierta con dos variables. Un elemento del conjunto de verdad de esta oración abierta (también llamada solución de la ecuación) es un par ordenado de números reales\((a, b)\) de manera que cuando a es sustituido por\(x\) y\(b\) es sustituido por\(y\), el predicado se convierte en una declaración verdadera (una ecuación verdadera en este caso). Podemos usar la notación del constructor de conjuntos para describir el conjunto\(S\) de verdad de esta ecuación con dos variables de la siguiente manera:

\(S = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ 4x^2 + y^2 = 16\}.\)

Cuando un conjunto es un conjunto de verdad de una oración abierta que es una ecuación, también llamamos al conjunto el conjunto de solución de la ecuación.

1. Enumere cuatro elementos diferentes del conjunto\(S\).
2. La gráfica de la ecuación\(4x^2 + y^2 = 16\) en el plano de coordenadas XY es una elipse. Dibuja la gráfica y explica por qué esta gráfica es una representación del conjunto de verdad (conjunto de soluciones) de la ecuación\(4x^2 + y^2 = 16\).
3. Describir cada uno de los siguientes conjuntos como un intervalo de números reales:
   
   (a)\(A = \{x \in \mathbb{R}\ |\ \text{there exists a } y \in \mathbb{R} \text{ such that } 4x^2 + y^2 = 16\}.\)
   (b)\(B = \{y \in \mathbb{R}\ |\ \text{there exists an } x \in \mathbb{R} \text{ such that } 4x^2 + y^2 = 16\}.\)

Introducción a las relaciones

En la Sección 6.1, introdujimos la definición formal de una función de un conjunto a otro conjunto. La noción de una función puede pensarse como una forma de relacionar los elementos de un conjunto con los de otro conjunto (o del mismo conjunto). Una función es un tipo especial de relación en el sentido de que cada elemento del primer conjunto, el dominio, está “relacionado” exactamente con un elemento del segundo conjunto, el codominio.

Esta idea de relacionar los elementos de un conjunto con los de otro conjunto usando pares ordenados no se restringe a las funciones. Por ejemplo, podemos decir que un entero,\(a\), está relacionado con otro entero,\(b\), siempre que\(a\) sea congruente con el\(b\) módulo 3. Observe que esta relación de congruencia módulo 3 proporciona una manera de relacionar un entero con otro entero. Sin embargo, en este caso, un entero\(a\) está relacionado con más de otro entero. Por ejemplo, desde

\(5 \equiv 5\)(mod 3),\(5 \equiv 2\) (mod 3) y\(5 \equiv -1\) (mod 3),

podemos decir que 5 está relacionado con 3, 5 está relacionado con 2, y 5 está relacionado con -1. Observe que, al igual que con las funciones, cada relación de la forma\(a \equiv b\) (mod 3) involucra dos integersa\(b\) y por lo tanto involucra un par ordenado\((a, b)\), que es un elemento de\(\mathbb{Z} \times \mathbb{Z}\).

Definición: relaciones

Dejar\(A\) y\(B\) ser conjuntos. Una relación\(R\) del conjunto\(A\) al conjunto\(B\) es un subconjunto de\(A \times B\). Es decir,\(R\) es una colección de pares ordenados donde la primera coordenada de cada par ordenado es un elemento de\(A\), y la segunda coordenada de cada par ordenado es un elemento de\(B\).

Una relación del conjunto\(A\) al conjunto\(A\) se llama relación en el conjunto\(A\). Entonces una relación en el conjunto\(A\) es un subconjunto de\(A \times A\).

En la Sección 6.1, definimos el dominio y el rango de una función. Hacemos definiciones similares para una relación.

Definición: Dominio y Rango

Si\(R\) es una relación del conjunto\(A\) al conjunto\(B\), entonces el subconjunto de\(A\) que consiste en todas las primeras coordenadas de los pares ordenados en\(R\) se llama el dominio de\(R\). El subconjunto de\(B\) que consiste en todas las segundas coordenadas de los pares ordenados en\(R\) se llama el rango de\(R\).

Usamos la notación dom (\(R\)) para el dominio de\(R\) y range (\(R\)) para el rango de\(R\). Entonces, usando la notación del constructor de conjuntos,

dom (\(R\))\(= \{u \in A\ |\ (u, y) \in R \text{ for at least one } y \in B\}\)

rango (\(R\))\(= \{v \in B\ |\ (x, v) \in R \text{ for at least one } x \in A\}\).

Ejemplo 7.1: Dominio y rango

Se estudió una relación en cada una de las Actividades Previas de esta sección. Para Vista previa de la Actividad 2, el conjunto\(S = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ 4x^2 + y^2 = 16\}\) es un subconjunto de\(\mathbb{R} \times \mathbb{R}\) y, por lo tanto,\(S\) es una relación sobre\(\mathbb{R}\). En Problema (3) de Actividad de Vista Previa\(\PageIndex{2}\), en realidad determinamos el dominio y el rango de esta relación.

dom (\(S\))\(= A = \{x \in \mathbb{R}\ |\ \text{there exists a } y \in \mathbb{R} \text{ such that } 4x^2 + y^2 = 16\}\)

rango (\(S\))\(= B = \{y \in \mathbb{R}\ |\ \text{there exists an } x \in \mathbb{R} \text{ such that } 4x^2 + y^2 = 16\}\)

Entonces, a partir de los resultados en Preview Activity\(\PageIndex{2}\), podemos decir que el dominio de la relación\(S\) es el intervalo cerrado [-2, 2] y el rango de S es el intervalo cerrado [-4, 4].

Comprobación de progreso 7.2: Ejemplos de relaciones

1. Vamos\(T = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ x^2 + y^2 = 64\}\).
   
   (a) Explicar por qué\(T\) es una relación sobre\(\mathbb{R}\).
   (b) Encontrar todos los valores de\(x\) tal que\((x, 4) \in T\). Encuentra todos los valores de\(x\) tal que\((x, 9) \in T\).
   c) ¿Cuál es el dominio de la relación\(T\)? ¿Cuál es el rango de\(T\)?
   (d) Dado que\(T\) es una relación sobre\(\mathbb{R}\), sus elementos pueden ser graficados en el plano de coordenadas. Describir la gráfica de la relación\(T\).
2. De Preview Activity\(\PageIndex{1}\),\(A\) es el conjunto de todos los estados de Estados Unidos, y
   \[R = \{(x, y) \in A \times A\ |\ x \text{ and } y \text{ have a border in common}\}.\]
   (a) Explicar por qué\(R\) es una relación sobre\(A\).
   b) ¿Cuál es el dominio de la relación\(R\)? ¿Cuál es el rango de la relación\(R\)?
   c) ¿Son verdaderas o falsas las siguientes afirmaciones? Justifica tus conclusiones.
   i. Para todos\(x, y \in A\), si\((x, y) \in R\), entonces\((y, x) \in R\).
   ii. Para todos\(x, y, z \in A\), si\((x, y) \in R\) y\((y, x) \in R\), entonces\((x, z) \in R\).

Contestar

Agrega textos aquí. No borre primero este texto.

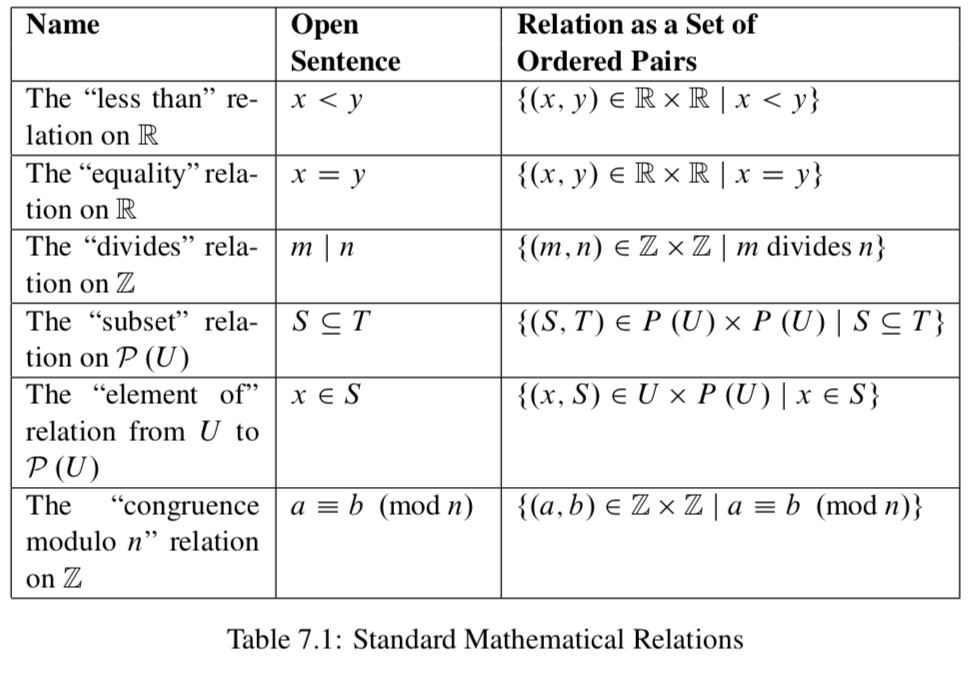
Algunas relaciones matemáticas estándar

Hay muchas relaciones diferentes en matemáticas. Por ejemplo, se puede considerar que dos números reales están relacionados si un número es menor que el otro número. A esto lo llamamos la relación “menos que” en\(\mathbb{R}\). Si\(x, y \in \mathbb{R}\) y\(x\) es menor que\(y\), a menudo escribimos\(x < y\). Como conjunto de pares ordenados, esta relación es\(R_{<}\), donde

\ {R_ {<} =\ {(x, y)\ in\ mathbb {R}\ veces\ mathbb {R}\ |\ x < y\}\).

Con muchas relaciones matemáticas, no escribimos la relación como un conjunto de pares ordenados aunque, técnicamente, se trate de un conjunto de pares ordenados. En el cuadro 7.1 se describen algunas relaciones matemáticas estándar.

Notación para las relaciones

Todas las relaciones matemáticas en la Tabla 7.1 utilizaron un símbolo de relación entre los dos elementos que forman el par ordenado en\(A \times B\). Por esta razón, muchas veces hacemos lo mismo para una relación general del conjunto\(A\) al conjunto\(B\). Entonces si\(R\) es una relación de\(A\) a\(B\),\(x \in A\) y y\(y \in B\), usamos la notación

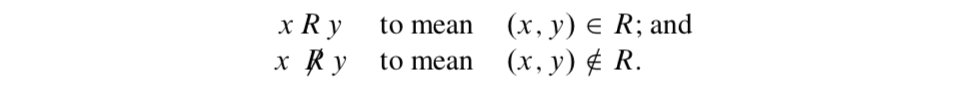
En algunos casos, incluso utilizaremos un símbolo de relación genérico para definir una nueva relación o hablar de relaciones en un contexto general. Quizás el símbolo de uso más común es “~”, leer “tilde” o “garabato” o “está relacionado con”. Cuando hagamos esto, escribiremos

\[\begin{array} {rcl} {x\ ~\ y} & \text{means the same thing as} & {(x, y) \in R;\text{ and}} \\ {x \nsim y} & \text{means the same thing as} & {(x, y) \notin R.} \end{array}\]

Comprobación de Progreso 7.3: La Relación Divide

Siempre que hemos hablado de un entero dividiendo otro entero, hemos trabajado con la relación “divide” en\(\mathbb{Z}\). En particular, podemos escribir

\(D = \{(m, n) \in \mathbb{Z} \times \mathbb{Z}\ |\ m \text{ divides } n\}.\)

En este caso, tenemos una notación específica para “divide”, y escribimos

\(m\ |\ n\)si y sólo si\((m, n) \in D\).

1. ¿Cuál es el dominio de la relación “divide”? ¿Cuál es el rango de la relación “divide”?
2. ¿Son verdaderas o falsas las siguientes afirmaciones? Explique.

   (a) Por cada entero distinto de cero\(a\),\(a\ |\ a\).
   (b) Para todos los enteros distintos de cero\(a\) y\(b\), si\(a\ |\ b\), entonces\(b\ |\ a\).
   (c) Para todos los enteros distintos de cero\(a\),\(b\), y\(c\), si\(a\ |\ b\) y\(b\ |\ c\), entonces\(a\ |\ c\).

Contestar

Agrega textos aquí. No borre primero este texto.

Funciones como Relaciones

Si tenemos una función\(f: A \to B\), podemos generar un conjunto de pares ordenados\(f\) que es un subconjunto de la\(A \times B\) siguiente manera:

\(f = \{(a, f(a))\ |\ a \in A\}\)o\(f = \{(a, b) \in A \times B\ |\ b = f(a)\}.\)

Esto quiere decir que\(f\) es una relación de\(A\) a\(B\). Ya que, dom (\(f\))\(= A\), sabemos que

(1) Por cada\(a \in A\), existe\(a, b \in B\) tal que\((a, b) \in f\).

Cuando\((a, b) \in f\)., escribimos\(b = f(a)\). Además, para ser una función, cada entrada puede producir solo una salida. En cuanto a pares ordenados, esto significa que nunca habrá dos pares ordenados\((a, b)\) y\(a, c)\) en la función\(f\), dónde\(a \in A\),\(b, c \in B\), y\(b = c\). Podemos formular esto como una declaración condicional de la siguiente manera:

(2) Por todos\(a \in A\) y cada uno\(b, c \in B\), si\((a, b) \in f\) y\((a, c) \in f\), entonces\(b = c\).

Esto significa que una función\(f\) de\(A\) a\(B\) es una relación de A a B que satisface las condiciones (1) y (2). (Ver Teorema 6.22 en la Sección 6.5.) No todas las relaciones, sin embargo, serán una función. Por ejemplo, considere la relación\(T\) en Avance Check 7.2.

Comprobación de progreso 7.4: Un conjunto de pares ordenados

Vamos\(F = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ y = x^2\}\). El conjunto\(F\) puede entonces ser considerado como relación en\(\mathbb{R}\) ya que es un subconjunto de\(\mathbb{R} \times \mathbb{R}\).

1. Enumere cinco pares ordenados diferentes que están en el conjunto\(F\).
2. Utilice el método roster para especificar los elementos de cada uno de los siguientes conjuntos:
   
   (a)\(A = \{x \in \mathbb{R}\ |\ (x, 4) \in F\}\)
   (b)\(B = \{x \in \mathbb{R}\ |\ (x, 10) \in F\}\)
   (c)\(C = \{y \in \mathbb{R}\ |\ (5, y) \in F\}\)
   (d)\(D = \{y \in \mathbb{R}\ |\ (-3, y) \in F\}\)
3. Dado que cada número real\(x\) produce solo un valor\(y\) para el cual\(y = x^2\), el conjunto se\(F\) puede utilizar para definir una función desde el conjunto\(\mathbb{R}\) hasta\(\mathbb{R}\). Dibuja una gráfica de esta función.

Contestar

Agrega textos aquí. No borre primero este texto.

Representaciones Visuales de Relaciones

En Avance Check 7.4, pudimos dibujar una gráfica de una relación como una forma de visualizar la relación. En este caso, la relación fue una función de\(\mathbb{R}\) a\(\mathbb{R}\). Además, en Progress Check 7.2, también pudimos usar una gráfica para representar una relación. En este caso, la gráfica de la relación\(T = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ x^2 + y^2 = 64\}\) es un círculo de radio 8 cuyo centro está en el origen.

Cuando\(R\) es una relación de un subconjunto de los números reales\(\mathbb{R}\) a un subconjunto de\(\mathbb{R}\), a menudo podemos usar una gráfica para proporcionar una representación visual de la relación. Esto es especialmente cierto si la relación está definida por una ecuación o incluso por una desigualdad. Por ejemplo, si

\(R = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ y \ge x^2\}\),

entonces podemos usar la siguiente gráfica como una forma de visualizar los puntos en el plano que también están en esta relación.

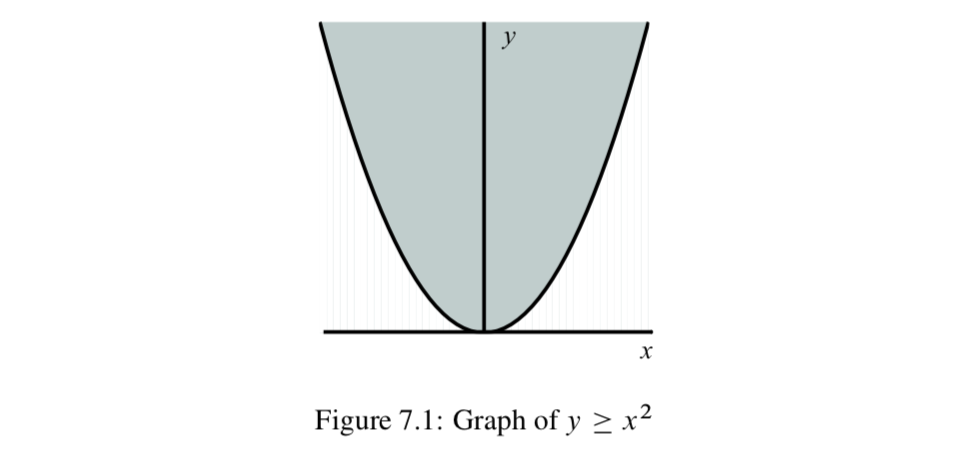
Los puntos\((x, y)\) en la relación\(R\) son los puntos en la gráfica de\(y = x^2\) o están en la región sombreada. Esto porque para estos puntos,\(y \ge x^2\). Una de las deficiencias de este tipo de gráficas es que la gráfica de la ecuación y la región sombreada están en realidad sin delimitar y así nunca podremos mostrar la gráfica completa de esta relación. No obstante, sí nos permite ver que los puntos en esta relación están o bien en la parábola definida por la ecuación\(y = x^2\) o están “dentro” de la parábola.

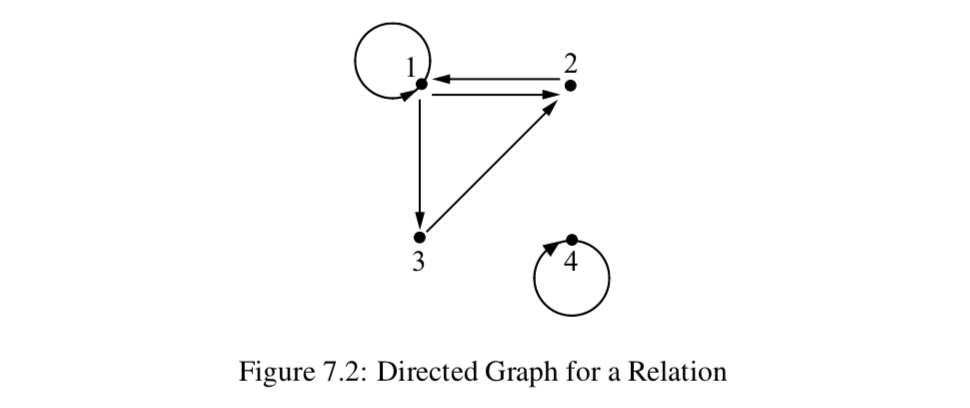
Cuando el dominio o rango de una relación es infinito, no podemos proporcionar una visualización de toda la relación. Sin embargo, si\(A\) es un conjunto finito (pequeño), se\(A\) puede especificar una relación\(R\) on simplemente enumerando todos los pares ordenados en\(R\). Por ejemplo, si\(A = \{1, 2, 3, 4\}\), entonces

\(R = \{(1, 1), (4, 4), (1, 3), (3, 2), (1, 2), (2, 1)\}\)

es una relación sobre\(A\). Una manera conveniente de representar tal relación es dibujar un punto en el plano para cada uno de los elementos de\(A\) y luego para cada\((x, y) \in R\) (o\(x\ R\ y\)), dibujamos una flecha comenzando en el punto\(x\) y apuntando al punto\(y\). Si\((x, x) \in R\) (o\(x\ R\ x\)), dibujamos un bucle en el punto\(x\). El diagrama resultante se llama gráfico dirigido o dígrafo. El diagrama de la Figura 7.2 es un dígrafo para la relación\(R\).

En una gráfica dirigida, los puntos se llaman los vértices. Entonces cada elemento de\(A\) corresponde a un vértice. Las flechas, incluyendo los bucles, se llaman los bordes dirigidos de la gráfica dirigida. Haremos uso de estas gráficas dirigidas en la siguiente sección cuando estudiemos las relaciones de equivalencia.

Comprobación de Progreso 7.5: La Gráfica Dirigida de una Relación

Vamos\(A = \{1, 2, 3, 4, 5, 6\}\). Dibuja una gráfica dirigida para las siguientes dos relaciones en el conjunto\(A\). Para cada relación, puede ser útil disponer los vértices de\(A\) como se muestra en la Figura 7.3.

\(R = \{(x, y) \in A \times A\ |\ x \text{ divides } y\}\),\(T = \{(x, y) \in A \times A\ |\ x + y \text{ is even}\}\).

Contestar

Agrega textos aquí. No borre primero este texto.

Ejercicio 7.1

1. Dejar\(A = \{a, b, c\}\),\(B = \{p, q, r\}\), y dejar\(R\) ser el conjunto de pares ordenados definidos por\(R = \{(a, p), (b, q), (c, p), (a, q)\}\).
   
   (a) Utilice el método roster para enumerar todos los elementos de\(A \times B\). Explicar por qué se\(A \times B\) puede considerar como una relación de\(A\) a\(B\).
   (b) Explicar por qué\(R\) es una relación de\(A\) a\(B\).
   c) ¿Cuál es el dominio\(R\)? ¿Cuál es el rango de\(R\)?
2. Dejar\(A = \{a, b, c\}\) y dejar\(R = \{(a, a), (a, c), (b, b), (b, c), (c, a), (c, b)\}\) (así\(R\) es una relación en\(A\)). ¿Son verdaderas o falsas las siguientes afirmaciones? Explique.
   
   (a) Para cada uno\(x \in A\),\(x\ R\ x\).
   b) Por cada\(x, y \in A\), si\(x\ R\ y\), entonces\(y\ R\ x\).
   (c) Por cada\(x, y, z \in A\), si\(x\ R\ y\) y\(y\ R\ z\), entonces\(x\ R\ z\).
   (d)\(R\) es una función de\(A\) a\(A\).
3. \(A\)Sea el conjunto de todas las ciudadanas de Estados Unidos. \(D\)Sea la relación sobre\(A\) definida por Es
   \[D = \{(x, y) \in A \times A\ |\ x \text{ is a daughter of } y\}.\]
   decir,\(x\ D\ y\) significa que\(x\) es hija de\(y\).
   
   (a) Describir aquellos elementos de\(A\) que se encuentran en el dominio de\(D\).
   (b) Describir aquellos elementos de\(A\) que se encuentran en el rango de\(D\).
   c) ¿La relación es\(D\) una función de\(A\) a\(A\)? Explique.
4. Dejar\(U\) ser un conjunto no vacío, y dejar que\(R\) sea la “relación de subconjunto” en\(\mathcal{P}(U)\). Es decir,
   \[R = \{(S, T) \in \mathcal{P}(U) \times \mathcal{P}(U)\ |\ S \subseteq T\}.\]
   
   (a) Escribir la oración abierta\((S, T) \in R\) usando notación de subconjunto estándar.
   b) ¿Cuál es el dominio de esta relación de subconjuntos,\(R\)?
   c) ¿Cuál es el alcance de esta relación de subconjuntos,\(R\)?
   d) ¿Es\(R\) una función de\(\mathcal{P}(U)\) a\(\mathcal{P}(U)\)? Explique.
5. Dejar\(U\) ser un conjunto no vacío, y dejar que\(R\) sea el “elemento de” relación de\(U\) a\(\mathcal{P}(U)\). Es decir, a
   \[R = \{(x, S) \in U \times \mathcal{P}(U)\ |\ x \in S\}.\]
   ) ¿Cuál es el dominio de este “elemento de” relación,\(R\)?
   b) ¿Cuál es el alcance de este “elemento de” relación,\(R\)?
   c) ¿Es\(R\) una función de\(U\) a\(\mathcal{P}(U)\)? Explique.
6. Vamos\(S = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ x^2 + y^2 = 100\}\).
   
   a) Determinar el conjunto de todos los valores de\(x\) tal que\((x, 6) \in S\), y determinar el conjunto de todos los valores de\(x\) tal que\((x, 9) \in S\).
   (b) Determinar el dominio y el rango de la relación\(S\) y escribir cada conjunto utilizando la notación set builder.
   c) ¿La relación es\(S\) una función de\(\mathbb{R}\) a\(\mathbb{R}\)? Explique.
   (d) Dado que\(S\) es una relación sobre\(\mathbb{R}\), sus elementos pueden ser graficados en el plano de coordenadas. Describir la gráfica de la relación\(S\). ¿La gráfica es consistente con tus respuestas en Ejercicios (6a) a (6c)? Explique.
7. Repetir Ejercicio (6) usando la relación sobre\(\mathbb{R}\) definida por
   \[S = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ y = \sqrt{100 - x^2}\}.\]
   ¿Cuál es la conexión entre esta relación y la relación en el Ejercicio (6)?
8. Determinar el dominio y rango de cada una de las siguientes relaciones\(\mathbb{R}\) y esbozar la gráfica de cada relación.
   
   (a)\(R = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ x^2 + y^2 = 10\}\)
   (b)\(S = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ y^2 = x + 10\}\)
   (c)\(T = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ |x| + |y| = 10\}\)
   (d)\(R = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ x^2 = y^2\}\)
9. \(R\)Sea la relación sobre\(\mathbb{Z}\) dónde para todos\(a, b \in \mathbb{Z}\),\(a\ R\ b\) si y sólo si\(|a - b| \le 2\).
   
   (a) Utilice la notación del constructor de conjuntos para describir la relación\(R\) como un conjunto de pares ordenados.
   b) Determinar el dominio y el rango de la relación\(R\).
   (c) Utilice el método de lista para especificar estos para que caigan enteros\(x\) tales que\(x\ R\ 5\) y el conjunto de todos los enteros\(x\) tales que\(5\ R\ x\).
   d) Si es posible, encontrar números enteros\(x\) y\(y\) tal que\(x\ R\ 8\),\(8\ R\ y\), pero.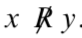
   (e) Si\(a \in \mathbb{Z}\), utilizar el método de lista para especificar el conjunto de todos los\(x \in \mathbb{Z}\) tales que\(x\ R\ a\).
10. Vamos\(R_{<} = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ x < y\}\). Esto quiere decir que\(R_{<}\) es la relación “menos que” en\(\mathbb{R}\).
    
    a) ¿Cuál es el dominio de la relación\(R_{<}\)?
    b) ¿Cuál es el alcance de la relación\(R_{<}\)?
    c) ¿La relación es\(R_{<}\) una función de\(\mathbb{R}\) a\(\mathbb{R}\)? Explique.
    
    Nota: Recuerda que una relación es un conjunto. En consecuencia, podemos hablar de que una relación es un subconjunto de otra relación. Otra cosa a recordar es que los elementos de una relación son pares ordenados.
    
    Exploraciones y actividades
11. El inverso de una relación. En la Sección 6.5, se introdujo la inversa de una función. Si\(A\) y\(B\) son conjuntos no vacíos y si\(f: A \to B\) es una función, entonces la inversa de\(f\), denotada por\(f^{-1}\), se define como
    \[\begin{array} {rcl} {f^{-1}} &= & {\{(b, a) \in B \times A\ |\ f(a) = b\}} \\ {} &= & {\{(b, a) \in B \times A\ |\ (a, b) \in f\}.} \end{array}\]
    Ahora que sabemos de relaciones, vemos que siempre\(f^{-1}\) es una relación de\(B\) a \(A\). El concepto de la inversa de una función es en realidad un caso especial del concepto más general de la inversa de una relación, que ahora definimos.

    Definición

    Dejar\(R\) ser una relación del conjunto\(A\) al conjunto\(B\). El inverso de\(R\), escrito\(R^{-1}\) y leído "\(R\)inverso”, es la relación de\(B\) a\(A\) definido por
    \[\begin{array} {rcl} {R^{-1}} &= & {\{(y, x) \in B \times A\ |\ (x, y) \in R\},\text{ or}} \\ {R^{-1}} &= & {\{(y, x) \in B \times A\ |\ x\ R\ y\}.} \end{array}\]

    Es decir,\(R^{-1}\) es el subconjunto de\(B \times A\) que consiste en todos los pares ordenados\((y, x)\) tal que\(x\ R\ y\).

    Por ejemplo, dejemos\(D\) ser la relación de “divide” en\(\mathbb{Z}\). Ver Comprobación de Progreso 7.3. Entonces
    \[D = \{(m, n) \in \mathbb{Z} \times \mathbb{Z}\ |\ m \text{ divides } n\}.\]
    

    Esto quiere decir que podemos escribir\(m\ |\ n\) si y solo si\((m, n) \in D\). Entonces, en este caso,
    \[\begin{array} {rcl} {D^{-1}} &= & {\{(n, m) \in \mathbb{Z} \times \mathbb{Z}\ |\ (m, n) \in D\}} \\ {} &= & {\{(n, m) \in \mathbb{Z} \times \mathbb{Z}\ |\ m \text{ divides } n\}.} \end{array}\]
    Ahora, si quisiéramos enfocarnos en la primera coordenada en lugar de la segunda coordenada en\(D^{-1}\), sabemos que “\(m\)divide\(n\)” significa lo mismo que “\(n\)es un múltiplo de”\(m\). De ahí,
    \[D^{-1} = \{(n, m) \in \mathbb{Z} \times \mathbb{Z}\ |\ n \text{ is a multiple of } m\}.\]
    podemos decir que la inversa de la relación “divide” en\(\mathbb{Z}\) es la relación “es un múltiplo de” en\(\mathbb{Z}\).
    El teorema 7.6, que sigue, contiene algunos hechos elementales sobre la inversa.

    Teorema 7.6.

    Dejar\(R\) ser una relación del conjunto\(A\) al conjunto\(B\). Entonces

    • El dominio de\(R^{-1}\) es el rango de\(R\). Es decir, dom (\(R^{-1}\)) = range (\(R\)).
    • El rango de\(R^{-1}\) es el dominio de\(R\). Es decir, range (\(R^{-1}\)) = dom (\(R\)).
    • El inverso de\(R^{-1}\) es R. Es decir,\((R^{-1})^{-1} = R\).

    Para probar la primera parte del Teorema 7.6, observar que el objetivo es demostrar que dos conjuntos son iguales,

    dom (\(R^{-1}\)) = rango (\(R\))

    Una forma de hacerlo es probar que cada uno es un subconjunto del otro. Para probar ese dom (\(R^{-1}\))\(\subseteq\) range (\(R\)), podemos comenzar eligiendo un elemento arbitrario de dom (\(R^{-1}\)). Así que vamos a\(y \in\) dom (\(R^{-1}\)). El objetivo ahora es demostrar ese\(y \in\) rango (\(R\)). ¿Qué significa decir que\(y \in\) dom (\(R^{-1}\))? Significa que existe\(x \in A\) tal que

    \((y, x) \in R^{-1}\).

    Ahora, ¿qué significa decir eso\((y, x) \in R^{-1}\)? Significa eso\((x, y) \in R\). ¿Qué nos dice esto\(y\)?

    Completar la prueba de la primera parte del Teorema 7.6. Después, completar las pruebas de las otras dos partes del Teorema 7.6.

    Prueba

    Agrega prueba aquí y automáticamente se ocultará

Contestar

Agrega textos aquí. No borre primero este texto.