7.2: Relaciones de equivalencia

Última actualización
Guardar como PDF

Page ID: 116070

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Vista previa de la actividad$\PageIndex{1}$: Properties of Relations

En cursos previos de matemáticas, hemos trabajado con la relación de igualdad. Por ejemplo, que R sea la relación en$\mathbb{Z}$ definida de la siguiente manera: Para todos$a, b \in \mathbb{Z}$,$a\ R\ b$ si y solo si$a = b$. Sabemos que esta relación de igualdad$\mathbb{Z}$ tiene las siguientes propiedades:

Para cada uno$a \in \mathbb{Z}$,$a = b$ y así$a\ R\ a$.
Para todos$a, b \in \mathbb{Z}$, si$a = b$, entonces$b = a$. Es decir, si$a\ R\ b$, entonces$b\ R\ a$.
Para todos$a, b, c \in \mathbb{Z}$, si$a = b$ y$b = c$, entonces$a = c$. Es decir, si$a\ R\ b$ y$b\ R\ c$, entonces$a\ R\ c$.

En matemáticas, cuando algo satisface ciertas propiedades, a menudo preguntamos si otras cosas satisfacen las mismas propiedades. Antes de investigar esto, daremos nombres a estas propiedades.

Definición

Dejar$A$ ser conjunto no vacío y dejar$R$ ser una relación en$A$.

La relación$R$ es reflexiva$A$ siempre que para cada uno$x \in A$,$x\ R\ x$ o, de manera equivalente,$(x, x) \in R$.
La relación$R$ es simétrica siempre que para cada$x, y \in A$, si$x\ R\ y$, entonces$y\ R\ x$ o, equivalentemente, para cada$x, y \in A$, si$(x, y) \in R$, entonces$(y, x) \in R$.
La relación$R$ es transitiva siempre que para cada$x, y, z \in A$, si$x\ R\ y$ y$y\ R\ z$, entonces$x\ R\ z$ o, equivalentemente, para cada$x, y, z \in A$, si$(x, y) \in R$ y$(y, z) \in R$, entonces$(x, z) \in R$.

Antes de explorar ejemplos, para cada una de estas propiedades, es una buena idea entender lo que significa decir que una relación no satisface la propiedad. Así que dejemos$A$ ser un conjunto no vacío y dejemos$R$ ser una relación sobre$A$.

Explique cuidadosamente lo que significa decir que la relación no$R$ es reflexiva en el set$A$.
Explique cuidadosamente lo que significa decir que la relación no$R$ es simétrica.
Explique cuidadosamente lo que significa decir que la relación no$R$ es transitiva.
Para ilustrar estas propiedades, dejamos$A = \{1, 2, 3, 4\}$ y definimos las relaciones$R$ y$T$ sucesivamente de la$A$ siguiente manera:
\[\begin{array} {rcl} {R} &= & {\{(1, 1), (2, 2), (3, 3), (4, 4), (1, 3), (3, 2)\}} \\ {T} &= & {\{(1, 1), (1, 4), (2, 4), (4, 1), (4, 2)\}} \end{array}\]
Dibuja una gráfica dirigida para la relación$R$. Entonces explique por qué la relación$R$ es reflexiva$A$, no es simétrica, y no es transitiva.
Dibuja una gráfica dirigida para la relación$T$. ¿La relación es$T$ reflexiva$A$? ¿La relación es$T$ simétrica? ¿La relación es$T$ transitiva? Explique.

Vista previa de la actividad$\PageIndex{2}$: Review of Congruence Modulo $n$

Dejar$a, b \in \mathbb{Z}$ y dejar$n \in \mathbb{N}$. En la página 92 de la Sección 3.1, definimos lo que significa decir que$a$ es congruente con el$b$ módulo$n$. Escribe esta definición y establece dos condiciones distintas que sean equivalentes a la definición.
Explicar por qué la congruencia módulo n es una relación sobre$\mathbb{Z}$.
Revisar cuidadosamente el Teorema 3.30 y las pruebas dadas en la página 148 de la Sección 3.5. En cuanto a las propiedades de las relaciones introducidas en Preview Activity$\PageIndex{1}$, ¿qué dice este teorema sobre la relación de congruencia módulo non los enteros?
Escriba una declaración completa del Teorema 3.31 en la página 150 y Corolario 3.32.
Escribir un comprobante de la propiedad simétrica para módulo de congruencia$n$. Es decir, probar lo siguiente:

Dejar$a, b \in \mathbb{Z}$ y dejar$n \in \mathbb{N}$. Si$a \equiv b$ (mod$n$), entonces$b \equiv a$ (mod$n$).

Gráficas dirigidas y propiedades de las relaciones

En la Sección 7.1, utilizamos gráficas dirigidas, o dígrafos, para representar relaciones en conjuntos finitos. Tres propiedades de relaciones se introdujeron en la Actividad de Vista Previa$\PageIndex{1}$ y se repetirán en las siguientes descripciones de cómo se pueden visualizar estas propiedades en una gráfica dirigida.

Dejar$A$ ser un conjunto no vacío y dejar que R sea una relación en$A$.

La relación$R$ es reflexiva$A$ siempre que para cada uno$x \in A$,$x\ R\ x$ o, de manera equivalente,. $(x, x) \in R$. Esto significa que si se representa una relación reflexiva en un dígrafo, tendría que haber un bucle en cada vértice, como se muestra en la siguiente figura.

$2019-04-05 3.26.30.png$

La relación$R$ es simétrica siempre que para cada$x, y \in A$, si$x\ R\ y$, entonces$y\ R\ x$ o, equivalentemente, para cada$x, y \in A$, si$(x, y) \in R$, entonces$(y, x) \in R$.
Esto significa que si se representa una relación simétrica en un dígrafo, entonces cada vez que hay un borde dirigido de un vértice a un segundo vértice, habría un borde dirigido desde el segundo vértice al primer vértice, como se muestra en la siguiente figura.

$2019-04-05 3.28.25.png$

La relación$R$ es transitiva siempre que para cada$x, y, z \in A$, si$x\ R\ y$ y$y\ R\ z$, entonces$x\ R\ z$ o, equivalentemente, para cada$x, y, z \in A$, si$(x, y) \in R$ y$(y, z) \in R$, entonces$(x, z) \in R$. Entonces, si una relación transitiva está representada por un dígrafo, entonces cada vez que hay un borde dirigido de un vértice$x$ a un vértice$y$ y un borde dirigido de y a un vértice$z$, habría un borde dirigido de$x$ a$z$.
Además, si una relación transitiva está representada por un dígrafo, entonces cada vez que hay un borde dirigido de un vértice$x$ a un vértice$y$ y un borde dirigido desde$y$ el vértice$x$, habría bucles en$x$ y$y$. Estas dos situaciones se ilustran de la siguiente manera:

$2019-04-05 3.32.52.png$

Comprobación de Progreso 7.7: Propiedades de las Relaciones

Dejar$A = \{a, b, c, d\}$ y dejar$R$ ser la siguiente relación sobre$A$:

$R = \{(a, a), (b, b), (a, c), (c, a), (b, d), (d, b)\}.$

Dibuje una gráfica dirigida para la relación$R$ y luego determine si la relación$R$ es reflexiva$A$, si la relación$R$ es simétrica y si la relación$R$ es transitiva.

Contestar: Agrega textos aquí. No elimine primero este texto.

Definición de una relación de equivalencia

En matemáticas, como en la vida real, a menudo es conveniente pensar en dos cosas diferentes como esencialmente iguales. Por ejemplo, cuando vas a una tienda a comprar un refresco frío, las latas de refrescos en la hielera suelen estar ordenadas por marca y tipo de refresco. Las Coca Colas se agrupan, las Pepsi Colas se agrupan, los Dr. Peppers se agrupan, y así sucesivamente. Cuando elegimos una lata particular de un tipo de refresco, estamos asumiendo que todas las latas son esencialmente iguales. A pesar de que las latas específicas de un tipo de refresco son físicamente diferentes, no hace diferencia cuál podemos elegir. Al hacer esto, estamos diciendo que las latas de un tipo de refresco son equivalentes, y estamos utilizando la noción matemática de una relación de equivalencia.

Una relación de equivalencia en un conjunto es una relación con una cierta combinación de propiedades que nos permiten ordenar los elementos del conjunto en ciertas clases. En esta sección, nos centraremos en las propiedades que definen una relación de equivalencia, y en la siguiente sección, veremos cómo estas propiedades nos permiten ordenar o dividir los elementos del conjunto en ciertas clases.

Definición: relación de equivalencia

Dejar$A$ ser un conjunto no vacío. Una relación$\sim$ sobre el conjunto$A$ es una relación de equivalencia siempre que$\sim$ sea reflexiva, simétrica y transitiva. Porque$a, b \in A$, si$\sim$ es una relación de equivalencia sobre$A$ y$a$$\sim$$b$, decimos que $a$es equivalente a$b$.

La mayoría de los ejemplos que hemos estudiado hasta ahora han implicado una relación sobre un pequeño conjunto finito. Para estos ejemplos, fue conveniente utilizar una gráfica dirigida para representar la relación. Ahora es el momento de mirar algún otro tipo de ejemplos, que pueden resultar más interesantes. En estos ejemplos, hay que tener en cuenta que existe una sutil diferencia entre la propiedad reflexiva y las otras dos propiedades. La propiedad reflexiva establece que algunos pares ordenados pertenecen realmente a la relación$R$, o algunos elementos de$A$ están relacionados. La propiedad reflexiva tiene un cuantificador universal y, de ahí, debemos probarlo para todos$x \in A$,$x\ R\ x$. La simetría y la transitividad, por otro lado, se definen por oraciones condicionales. A menudo utilizamos una prueba directa para estas propiedades, y así comenzamos asumiendo la hipótesis y luego mostrando que la conclusión debe seguir de la hipótesis.

Ejemplo 7.8: Una relación que no es una relación de equivalencia

$M$Sea la relación sobre$\mathbb{Z}$ definida de la siguiente manera:

Para$a, b \in \mathbb{Z}$,$a\ M\ b$ si y solo si$a$ es un múltiplo de$b$.

Entonces$a\ M\ b$ si y sólo si existe$k \in \mathbb{Z}$ tal eso$a = bk$.

La relación$M$ es reflexiva$\mathbb{Z}$ desde para cada uno$x \in \mathbb{Z}$,$x = x \cdot 1$ y, por lo tanto,$x\ M\ x$.
Observe eso$4\ M\ 2$, pero 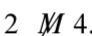$2019-04-05 3.45.34.png$ Entonces existen enteros$x$ y$y$ tal que$x\ M\ y$ pero 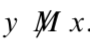$2019-04-05 3.46.17.png$ Por lo tanto, la relación no$M$ es simétrica.
Ahora supongamos que$x\ M\ y$ y$y\ M\ z$. Entonces existen enteros$p$ y$q$ tal que
\[x = yp \text{ and } y = zq.\]
Usando la segunda ecuación para hacer una sustitución en la primera ecuación, vemos eso$x = z(pq)$. Ya que$pq \in \mathbb{Z}$, hemos demostrado que$x$ es un múltiplo de$z$ y por lo tanto$x\ M\ z$. Por lo tanto,$M$ es una relación transitiva.

La relación$M$ es reflexiva$\mathbb{Z}$ y transitiva, pero como no$M$ es simétrica, no es una relación de equivalencia sobre$\mathbb{Z}$.

Solución

Agrega texto aquí.

Comprobación de progreso 7.9 (una relación que es una relación de equivalencia)

Defina la relación$\sim$ de la$\mathbb{Q}$ siguiente manera: Para todos$a, b \in Q$,$a$$\sim$$b$ si y solo si$a - b \in \mathbb{Z}$. Por ejemplo:

$\dfrac{3}{4}$$\sim$$\dfrac{7}{4}$desde$\dfrac{3}{4} - \dfrac{7}{4} = -1$ y$-1 \in \mathbb{Z}$.
$\dfrac{3}{4} \nsim \dfrac{1}{2}$desde$\dfrac{3}{4} - \dfrac{1}{2} = \dfrac{1}{4}$ y$\dfrac{1}{4} \notin \mathbb{Z}$.

Para probar eso$\sim$ es reflexivo$\mathbb{Q}$, observamos que para todos$q \in \mathbb{Q}$,$a - a = 0$. Ya que$0 \in \mathbb{Z}$, concluimos que$a$$\sim$$a$. Ahora demuestre que la relación$\sim$ es simétrica y transitiva, y por lo tanto, esa$\sim$ es una relación de equivalencia sobre$\mathbb{Q}$.

Contestar: Agrega textos aquí. No elimine primero este texto.

Congruencia Modulo$n$

Una de las relaciones de equivalencia importantes que estudiaremos en detalle es la del módulo de congruencia$n$. Revisamos esta relación en Actividad previa$\PageIndex{2}$.

El teorema 3.30 nos dice que congruencia módulo n es una relación de equivalencia sobre$\mathbb{Z}$. Recordemos que por el Algoritmo de División$a \in \mathbb{Z}$, si, entonces existen enteros únicos$q$ y$r$ tales que

$a = nq + r$y$0 \le r < n$.

Teorema 3.31 y Corolario 3.32 luego nos dicen que$a \equiv r$ (mod$n$). Es decir, a es congruente módulo n a su resto$r$ cuando se divide por$n$. Cuando usamos el término “resto” en este contexto, siempre nos referimos al resto$r$ con$0 \le r < n$ eso garantizado por el Algoritmo de División. Podemos usar esta idea para probar el siguiente teorema.

Teorema 7.10

Dejar$n \in \mathbb{N}$ y dejar$a, b \in \mathbb{Z}$. Entonces$a \equiv b$ (mod$n$) si y solo si$a$ y$b$ tener el mismo resto cuando se divide por$n$.

Prueba

Dejar$n \in \mathbb{N}$ y dejar$a, b \in \mathbb{Z}$. Primero probaremos que si$a$ y$b$ tenemos el mismo resto cuando se divide por$n$, entonces$a \equiv b$ (mod$n$). Entonces supongamos que a y bhave el mismo resto cuando se divide por$n$, y deja$r$ ser este resto común. Entonces, por el Teorema 3.31,

$a \equiv r$(mod$n$) y$b \equiv r$ (mod$n$).

Dado que el módulo de congruencia$n$ es una relación de equivalencia, es una relación simétrica. De ahí, desde$b \equiv r$ (mod$n$), podemos concluir que$r \equiv b$ (mod$n$). Combinando esto con el hecho de que$a \equiv r$ (mod$n$), ahora tenemos

$a \equiv r$(mod$n$) y$r \equiv b$ (mod$n$)

Ahora podemos usar la propiedad transitiva para concluir que$a \equiv b$ (mod$n$). Esto demuestra que si$a$ y$b$ tener el mismo resto cuando se divide por$n$, entonces$a \equiv b$ (mod$n$).

Ahora vamos a probar que si$a \equiv b$ (mod$n$), entonces$a$ y$b$ tener el mismo resto cuando se divide por$n$. Supongamos que$a \equiv b$ (mod$n$), y deja$r$ ser el resto menos no negativo cuando$b$ se divide por$n$. Entonces$0 \le r < n$ y, por el Teorema 3.31,

$b \equiv r$(mod$n$).

Ahora, usando los hechos que$a \equiv b$ (mod$n$) y$b \equiv r$ (mod$n$), podemos usar la propiedad transitiva para concluir que

$a \equiv r$(mod$n$)

Esto significa que existe un entero$q$ tal que$a - r = nq$ o que

$a = nq + r.$

Como ya sabemos eso$0 \le r < n$, la última ecuación nos dice que$r$ es el resto menos no negativo cuando$a$ se divide por$n$. De ahí que hayamos probado que si$a \equiv b$ (mod$n$), entonces$a$ y$b$ tener el mismo resto cuando se divide por$n$.

Ejemplos de Otras Relaciones de Equivalencia

La relación de$\sim$ la Comprobación$\mathbb{Q}$ de Progreso 7.9 es una relación de equivalencia.
Dejar$A$ ser un conjunto no vacío. La relación de igualdad$A$ es una relación de equivalencia. Esta relación también se llama la relación de identidad sobre$A$ y se denota por$I_{A}$, donde
\[I_{A} = \{(x, x)\ |\ x \in A\}.\]
Defina$\sim$ la relación de la$\mathbb{R}$ siguiente manera:
Para$a, b \in \mathbb{R}$,$a$$\sim$$b$ si y sólo si existe un entero$k$ tal que$a - b = 2k\pi$.

Demostraremos que la relación ~ es una relación de equivalencia sobre$\mathbb{R}$. La relación$\sim$ es reflexiva$\mathbb{R}$ ya que para cada uno$a \in \mathbb{R}$,$a - a = 0 = 2 \cdot 0 \cdot \pi$.
Ahora, dejemos$a, b \in \mathbb{R}$ y asuma eso$a$$\sim$$b$. Eso lo demostraremos$b$$\sim$$a$. Ya que$a$$\sim$$b$, existe un entero$k$ tal que
\[a - b = 2k\pi.\]
Al multiplicar ambos lados de esta ecuación por -1, obtenemos
\[\begin{array} {rcl} {(-1)(a - b)} &= & {(-1)(2k\pi)} \\ {b - a} &= & {2(-k)\pi.} \end{array}\]
Desde$-k \in \mathbb{Z}$, la última ecuación demuestra que $b$$\sim$$a$. De ahí que hayamos probado que si$a$$\sim$$b$, entonces$b$$\sim$$a$ y, por tanto, la relación$\sim$ es simétrica.

Para probar la transitividad, vamos$a, b, c \in \mathbb{R}$ y asumamos que$a$$\sim$$b$ y$b$$\sim$$c$. Eso lo demostraremos$a$$\sim$$c$. Ahora, existen enteros$k$ y$n$ tal que
\[a - b = 2k\pi \text{ and } b - c = 2n\pi.\]
Al sumar los lados correspondientes de estas dos ecuaciones, vemos que
\[\begin{array} {rcl} {(a - b) + (b - c)} &= & {2k\pi + 2n\pi} \\ {a - c} &= & {2(k + n)\pi.} \end{array}\]
Por las propiedades de cierre de los enteros,$k + n \in \mathbb{Z}$. Entonces esto prueba eso$a$$\sim$$c$ y, de ahí que la relación$\sim$ sea transitiva.

Ahora hemos demostrado que$\sim$ es una relación de equivalencia sobre$\mathbb{R}$. Esta relación de equivalencia es importante en la trigonometría. Si$a \sim b$, entonces existe un entero$k$ tal que$a - b = 2k\pi$ y, por lo tanto,$a = b + k(2\pi)$. Dado que las funciones seno y coseno son periódicas con un periodo de$2\pi$, vemos que
\[\begin{array} {rcl} {sin\ a} &= & {sin(b + k(2\pi)) = sin\ b \text{, and }} \\ {cos\ a} &= & {cos(b + k(2\pi)) = cos\ b.} \end{array}\]
Por lo tanto$a \sim b$, cuando, cada una de las funciones trigonométricas tienen el mismo valor en$a$ y$b$.
Para un ejemplo de geometría euclidiana, definimos una relación$P$ en el conjunto$\mathcal{L}$ de todas las líneas del plano de la siguiente manera:
Para$l_1, l_2 \in \mathcal{L}$,$l_1\ P\ l_2$ si y sólo si$l_1$ es paralelo a$l_2$ o$l_1 = l_2$.

Agregamos la segunda condición a la definición de$P$ para asegurar que$P$ sea reflexivo$\mathcal{L}$. Los teoremas de la geometría euclidiana nos dicen que si$l_1$ es paralelo a$l_2$, entonces$l_2$ es paralelo a$l_1$, y si$l_1$ es paralelo a$l_2$ y$l_2$ es paralelo a$l_3$, entonces$l_1$ es paralelo a$l_3$. (Dibujar imágenes ayudará a visualizar estas propiedades). Esto nos dice que la relación$P$ es reflexiva, simétrica y transitiva y, por lo tanto, una relación de equivalencia sobre$\mathcal{L}$.

Comprobación de Progreso 7.11: Otra Relación de Equivalencia

Dejar$U$ ser un conjunto finito, no vacío y dejar que$\mathcal{P}(U)$ sea el conjunto de potencia de$U$. Recordemos que$\mathcal{P}(U)$ consta de todos los subconjuntos de$U$. (Ver página 222.) Defina la relación$\approx$ de la$\mathcal{P}(U)$ siguiente manera:

Para$A, B \in P(U)$,$A \approx B$ si y solo si card ($A$) = card ($B$).

Para la definición de la cardinalidad de un conjunto finito, véase la página 223. Esta relación establece que dos subconjuntos de$U$ son equivalentes siempre que tengan el mismo número de elementos. Demostrar que$\approx$ es una relación de equivalencia en

Contestar: Agrega textos aquí. No elimine primero este texto.

Ejercicio 7.2

Dejar$A = \{a, b\}$ y dejar$R = \{(a, b)\}$. ¿Está$R$ encendida una relación de equivalencia$A$? Si no es así, ¿es$R$ reflexivo, simétrico o transitivo? Justificar todas las conclusiones
Vamos$A =\{a, b, c\}$. Para cada una de las siguientes, dibuje una gráfica dirigida que represente una relación con las propiedades especificadas.

(a) Una relación sobre$A$ eso es simétrica pero no transitiva
(b) Una relación sobre$A$ eso es transitiva pero no simétrica
(c) Una relación sobre$A$ eso es simétrica y transitiva pero no reflexiva sobre$A$
(d) Una relación sobre$A$ eso no es reflexiva$A$, no es simétrica, y no es transitiva
(e) Una relación sobre$A$, distinta de la relación de identidad, es decir, una relación de equivalencia sobre$A$
Vamos$A = \{1, 2, 3, 4, 5\}$. La relación de identidad en$A$ es
\[I_A = \{(1, 1), (2, 2), (3, 3), (4, 4), (5, 5)\}.\]
Determinar una relación de equivalencia sobre$A$ eso es diferente$I_A$ o explicar por qué esto no es posible.
Vamos$R = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ |x| + |y| = 4\}$. Entonces$R$ es una relación sobre$\mathbb{R}$. ¿Está$R$ encendida una relación de equivalencia$\mathbb{R}$? Si no es así, ¿es$R$ reflexivo, simétrico o transitivo? Justificar todas las conclusiones
Una relación$R$ se define de la$\mathbb{Z}$ siguiente manera: Para todos$a, b$ en$\mathbb{Z}$,$a\ R\ b$ si y solo si$|a - b| \le 3$. ¿Está$R$ encendida una relación de equivalencia$\mathbb{R}$? Si no es así, es$R$ reflexivo, simétrico o transitivo. Justificar todas las conclusiones
Dejar$f: \mathbb{R} \to \mathbb{R}$ ser definido por$f(x) = x^2 - 4$ para cada uno$x \in \mathbb{R}$. Defina una relación$\sim$ de la$\mathbb{R}$ siguiente manera:
Para$a, b \in \mathbb{R}$,$a \sim b$ si y solo si$f(a) = f(b)$.
a) ¿La relación es una relación de equivalencia sobre$\mathbb{R}$? Justifica tu conclusión.
(b) Determinar todos los números reales del conjunto$C = \{x \in R\ |\ x \sim 5\}.$
Repita Ejercicio (6) usando la función$f: \mathbb{R} \to \mathbb{R}$ que se define por$f(x) = x^2 - 3x - 7$ para cada uno$x \in \mathbb{R}$.
(a) Repetir Ejercicio (6a) usando la función$f: \mathbb{R} \to \mathbb{R}$ que se define por$f(x) = sin\ x$ para cada uno$x \in \mathbb{R}$.
(b) Determinar todos los números reales del conjunto$C = \{x \in \mathbb{R}\ |\ x \sim \pi\}$.
Defina la relación$\sim$ de la$\mathbb{Q}$ siguiente manera: Para$a, b \in \mathbb{Q}$,$a \sim b$ si y solo si$a - b \in \mathbb{Z}$. En progreso Check 7.9, demostramos que la relación$\sim$ es una relación de equivalencia sobre$\mathbb{Q}$.

(a) Listar cuatro elementos diferentes del conjunto$C = \{x \in \mathbb{Q}\ |\ x \sim \dfrac{5}{7}\}.$
(b) Utilice la notación del constructor de conjuntos (sin usar el símbolo$sim$) para especificar el conjunto$C$.
(c) Utilice el método de lista para especificar el conjunto$C$.
Dejar$\sim$ y$\approx$ ser relación en$\mathbb{Z}$ definido de la siguiente manera:

$\bullet$ Para$a, b \in Z$,$a \sim b$ si y sólo si 2 divide$a + b$.
$\bullet$Para$a, b \in Z$,$a \approx b$ si y solo si 3 divide$a + b$.

a) ¿Está$\sim$ encendida una relación de equivalencia$\mathbb{Z}$? Si no, ¿es esta relación reflexiva, simétrica o transitiva?
b) ¿Se$\approx$ aplica una relación de equivalencia$\mathbb{Z}$? Si no, ¿es esta relación reflexiva, simétrica o transitiva?
Dejar$U$ ser un conjunto finito, no vacío y dejar que$\mathcal{P}(U)$ sea el conjunto de potencia de$U$. Es decir,$\mathcal{P}(U)$ es el conjunto de todos los subconjuntos de$U$. Defina la relación$\sim$ de la$\mathcal{P}(U)$ siguiente manera: Para$A, B \in P(U)$,$A \sim B$ si y solo si$A \cap B = \emptyset$. Es decir, el par ordenado$(A, B)$ está en la relaiton$\sim$ si y sólo si$A$ y$B$ son disjuntos.
¿La relación es$\sim$ una relación de equivalencia$\mathcal{P}(U)$? Si no, ¿es reflexiva, simétrica o transitiva? Justificar todas las conclusiones
Dejar$U$ ser un conjunto no vacío y dejar que$\mathcal{P}(U)$ sea el conjunto de potencia de$U$. Es decir,$\mathcal{P}(U)$ es el conjunto de todos los subconjuntos de$U$.
Para$A$ y$B$ en$\mathcal{P}(U)$, definir$A \sim B$ para significar que existe una biyección$f: A \to B$. Demostrar que$\sim$ es una relación de equivalencia sobre$\mathcal{P}(U)$.
Pista: Utilice los resultados de las Secciones 6.4 y 6.5.
Dejar$\sim$ y$\approx$ ser relación en$\mathbb{Z}$ definido de la siguiente manera:

$\bullet$ Para$a, b \in Z$,$a \sim b$ si y solo si$2a + 3b \equiv 0$ (mod 5).
$\bullet$Para$a, b \in Z$,$a \approx b$ si y solo si$a + 3b \equiv 0$ (mod 5).

a) ¿Está$\sim$ encendida una relación de equivalencia$\mathbb{Z}$? Si no, ¿es esta relación reflexiva, simétrica o transitiva?
b) ¿Se$\approx$ aplica una relación de equivalencia$\mathbb{Z}$? Si no, ¿es esta relación reflexiva, simétrica o transitiva?
Dejar$\sim$ y$\approx$ ser relación en$\mathbb{R}$ definido de la siguiente manera:

$\bullet$ Para$a, b \in Z$,$a \sim b$ si y solo si$xy \ge 0$.
$\bullet$Para$a, b \in Z$,$a \approx b$ si y solo si$xy \le 0$.

a) ¿Está$\sim$ encendida una relación de equivalencia$\mathbb{R}$? Si no, ¿es esta relación reflexiva, simétrica o transitiva?
b) ¿Se$\approx$ aplica una relación de equivalencia$\mathbb{R}$? Si no, ¿es esta relación reflexiva, simétrica o transitiva?
Defina la relación$\approx$ de la$\mathbb{R} \times \mathbb{R}$ siguiente manera: Para$(a, b), (c, d) \in \mathbb{R} \times \mathbb{R}$,$(a, b) \approx (c, d)$ si y solo si$a^2 + b^2 = c^2 + d^2$.

a) Demostrar que$\approx$ es una relación de equivalencia sobre$\mathbb{R} \times \mathbb{R}$.
(b) Listar cuatro elementos diferentes del conjunto
\[C = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ (x, y) \approx (4, 3)\}.\]
(c) Dar una descripción geométrica del conjunto$C$.
Evaluación de pruebas
Consulte las instrucciones para Ejercicio (19) en la página 100 de la Sección 3.1.
(a)

Proposición. Que$R$ sea una relación en un set$A$. Si$R$ es simétrico y transitivo, entonces$R$ es reflexivo.

Prueba

Vamos$x, y \in A$. Si$x\ R\ y$, entonces$y\ R\ x$ ya$R$ es simétrico. Ahora,$x\ R\ y$ y$y\ R\ x$, y como$R$ es transitivo, podemos concluir eso$x\ R\ x$. Por lo tanto,$R$ es reflexivo.

b)

Proposición. Dejar$\sim$ ser una relación sobre$\mathbb{Z}$ dónde para todos$a, b \in \mathbb{Z}$,$a \sim b$ si y solo si$(a + 2b) \equiv 0$ (mod 3). La relación$\sim$ es una relación de equivalencia sobre$\mathbb{Z}$.

Prueba

Asumir$a \sim a$. Entonces$(a + 2a) \equiv 0$ (mod 3) desde$(3a) \equiv 0$ (mod 3). Por lo tanto,$\sim$ es reflexivo sobre$\mathbb{Z}$. Además, si$a \sim b$, entonces$(a + 2b) \equiv 0$ (mod 3), y si multiplicamos ambos lados de esta congruencia por 2, obtenemos

\[\begin{array} {rcl} {2(a + 2b)} &\equiv & {2 \cdot 0 \text{ (mod 3)}} \\ {(2a + 4b)} &\equiv & {0 \text{ (mod 3)}} \\ {(a + 2b)} &\equiv & {0 \text{ (mod 3)}} \\ {(b + 2a)} &\equiv & {0 \text{ (mod 3)}.} \end{array}\]

Esto quiere decir que$b\ \sim\ a$ y por lo tanto,$\sim$ es simétrico.

Ahora asumimos que$(a + 2b) \equiv 0$ (mod 3) y$(b + 2c) \equiv 0$ (mod 3).

Al sumar los lados correspondientes de estas dos congruencias, obtenemos

\[\begin{array} {rcl} {(a + 2b) + (b + 2c)} &\equiv & {0 + 0 \text{ (mod 3)}} \\ {(a + 3b + 2c)} &\equiv & {0 \text{ (mod 3)}} \\ {(a + 2c)} &\equiv & {0 \text{ (mod 3)}.} \end{array}\]

De ahí que la relación$\sim$ sea transitiva y hemos demostrado que$\sim$ es una relación de equivalencia sobre$\mathbb{Z}$.

Exploraciones y actividades

17. Otros Tipos de Relaciones. En esta sección, nos centramos en las propiedades de una relación que forman parte de la definición de una relación de equivalencia. Sin embargo, hay otras propiedades de las relaciones que son de importancia. Estudiaremos dos de estas propiedades en esta actividad.

Una relación$R$ sobre un conjunto$A$ es una relación circular siempre que para todos$x$,$y$, y$z$ en$A$, si$x\ R\ y$ y$y\ R\ z$, entonces$z\ R\ x$.

a) Explique cuidadosamente lo que significa decir que una relación$R$ en un conjunto no$A$ es circular.

b) Dejar$A = \{1, 2, 3\}$. Dibuja una gráfica dirigida de una relación sobre la$A$ que sea circular y dibuje una gráfica dirigida de una relación sobre la$A$ que no sea circular.
(c) Dejar$A = \{1, 2, 3\}$. Dibuja una gráfica dirigida de una relación sobre la$A$ que sea circular y no transitiva y dibuje una gráfica dirigida de una relación sobre la$A$ que sea transitiva y no circular.

d) Demostrar la siguiente proposición:
Una relación$R$ sobre un conjunto$A$ es una relación de equivalencia si y sólo si es reflexiva y circular.

Una relación$R$ sobre un conjunto$A$ es una relación antisimétrica siempre que para todos$x, y \in A$, si$x\ R\ y$ y$y\ R\ x$, entonces$x = y$.

e) Explique cuidadosamente lo que significa decir que una relación sobre un conjunto no$A$ es antisimétrica.

(f) Dejar$A = \{1, 2, 3\}$. Dibuja una gráfica dirigida de una relación sobre la$A$ que sea antisimétrica y dibuje una gráfica dirigida de una relación sobre la$A$ que no sea antisimétrica.

g) ¿Son verdaderas o falsas las siguientes proposiciones? Justificar todas las conclusiones

Si una relación$R$ en un conjunto$A$ es simétrica y antisimétrica, entonces$R$ es transitiva.
Si una relación$R$ en un conjunto$A$ es simétrica y antisimétrica, entonces$R$ es reflexiva.

Contestar: Agrega textos aquí. No elimine primero este texto.

Vista previa de la actividad\(\PageIndex{1}\): Properties of Relations