Apéndice B: Respuestas para las comprobaciones de progreso
- Page ID
- 116065
Sección 1.1
Comprobación de progreso 1.2
- Esta proposición es falsa. Un contraejemplo es\(a = 2\) y\(b = 1\). Por estos valores,\((a + b)^2 = 9\) y\(a^2 + b^2 = 5\).
- Esta proposición es cierta, como podemos ver usando\(x = 3\) y\(y = 7\). También podríamos usar\(x = -2\) y\(y = 9\). Hay muchas otras opciones posibles para\(x\) y\(y\).
- Esta proposición parece ser cierta. Cada vez que usamos un ejemplo donde\(x\) es un número entero par, el número\(x^2\) es un número entero par. Sin embargo, no podemos afirmar que esto sea cierto en base a ejemplos ya que no podemos enumerar todos los ejemplos donde\(x\) es un número entero par.
- Esta proposición parece ser cierta. Cada vez que usamos un ejemplo donde\(x\) y\(y\) son ambos enteros, el número\(x \cdot y\) es un entero impar. Sin embargo, no podemos afirmar que esto sea cierto en base a ejemplos ya que no podemos enumerar todos los ejemplos donde tanto x como y son enteros impares.
Comprobación de progreso 1.4
- (a) Esto no significa que la declaración condicional sea falsa ya que cuando\(x = -3\), la hipótesis es falsa, y la única vez que una declaración condicional es falsa es cuando la hipótesis es verdadera y la conclusión es falsa.
(b) Esto no quiere decir que la declaración condicional sea cierta ya que no hemos comprobado todos los números reales positivos, sólo aquel en el que\(x = 4\).
(c) All examples should indicate that the conditional statement is true. - El número (\(n2 - n + 41\)) will be a prime number for all examples of \(n\) that are less than 41. However, when \(n = 41\), we get
\[\begin{array} {rcl} {n^2 - n + 41} &= & {41^2 - 41 + 41} \\ {n^2 - n + 41} &= & {41^2} \end{array}\]
Entonces en el caso donde\(n = 41\), la hipótesis es verdadera (41 es un entero positivo) y la conclusión es falsa (no\(41^2\) es primo). Por lo tanto, 41 es un contraejemplo que muestra que la declaración condicional es falsa. Hay otros contraejemplos (como\(n = 42\),\(n = 45\), y\(n = 50\)), pero solo se necesita un contraejemplo para probar que la declaración es falsa.
Comprobación de progreso 1.5
- Podemos concluir que esta función es continua a 0.
- No podemos sacar conclusiones sobre esta función a partir del teorema.
- No podemos sacar conclusiones sobre esta función a partir del teorema.
- Podemos concluir que esta función no es diferenciable a 0.
Comprobación de progreso 1.7
- El conjunto de números racionales se cierra bajo suma desde entonces\(\dfrac{a}{b} + \dfrac{c}{d} = \dfrac{ad + bc}{bd}\).
- El conjunto de enteros no se cierra bajo división. Por ejemplo, no\(\dfrac{2}{3}\) es un entero.
- El conjunto de números racionales se cierra bajo resta ya que\(\dfrac{a}{b} - \dfrac{c}{d} = \dfrac{ad - bc}{bd}\).
Sección 1.2
Comprobación de Progreso 1.10
Todos los ejemplos deben indicar que la proposición es verdadera. A continuación se presenta una prueba.
Comprobante. Suponemos que\(m\) es un entero impar y probaremos que (\(3m^2 + 4m + 6\)). Dado que\(m\) es un entero impar, existe un entero\(k\) tal que\(m D= 2k + 1\). Sustituyendo esto en la expresión (\(3m^2 + 4m + 6\)) y usando álgebra, obtenemos
\(\begin{array} {rcl} {3m^2 + 4m + 6} &= & {3(2k + 1)^2 + 4(2k + 1) + 6} \\ {} &= & {(12k^2 + 12k + 3) + (8k + 4) + 6} \\ {} &= & {12k^2 + 20k + 13} \\ {} &= & {12k^2 + 20k + 12 + 1} \\ {} &= & {2(6k^2 + 10k + 6) + 1} \end{array}\)
Comprobación de Progreso 1.11
Prueba. Dejamos\(m\) ser un número real y asumimos que\(m\)\(m + 1\),, y\(m + 2\) son las longitudes de los tres lados de un triángulo rectángulo. Utilizaremos el Teorema de Pitágoras para demostrarlo\(m = 3\). Dado que la hipotenusa es el más largo de los tres lados, el Teorema de Pitágoras implica eso\(m^2 + (m + 1)^2 = (m + 2)^2\). Ahora usaremos álgebra para reescribir ambos lados de esta ecuación de la siguiente manera:
\(\begin{array} {rcl} {m^2 + (m^2 + 2m + 1)} &= & {m^2 + 4m + 4} \\ {2m^2 + 2m + 1} &= & {m^2 + 4m + 4} \end{array}\)
La última ecuación es una ecuación cuadrática. Para resolver\(m\), reescribimos la ecuación en forma estándar y luego factorizamos el lado izquierdo. Esto da
\(\begin{array} {rcl} {m^2 - 2m - 3} &= & {0} \\ {(m - 3) (m + 1)} &= & {0} \end{array}\)
Las dos soluciones de esta ecuación son\(m = 3\) y\(m = -1\). No obstante, dado que\(m\) es la longitud de un lado de un triángulo rectángulo,\(m\) debe ser positivo y concluimos que\(m = 3\). Esto demuestra que si\(m\),\(m + 1\), y\(m + 2\) son las longitudes de los tres lados de un triángulo rectángulo, entonces\(m = 3\).
Sección 2.1
Comprobación de progreso 2.1
- Siempre que un cuadrilátero es un cuadrado, es un rectángulo, o un cuadrilátero es un rectángulo siempre que sea un cuadrado.
- Un cuadrilátero es un cuadrado sólo si es un rectángulo.
- Ser un rectángulo es necesario para que un cuadrilátero sea un cuadrado.
- Ser un cuadrado es suficiente para que un cuadrilátero sea un rectángulo.
Comprobación de progreso 2.2
| \(P\) | \(Q\) | \(P \wedge \urcorner Q\) | \(\urcorner (P \wedge Q)\) | \(\urcorner P \wedge \urcorner Q\) | \(\urcorner P \vee \urcorner Q\) |
| T | T | F | F | F | F |
| T | F | T | T | F | T |
| F | T | F | T | F | T |
| F | F | F | T | T | T |
Las declaraciones (2) y (4) tienen la misma tabla de verdad.
Comprobación de progreso 2.4
| \(P\) | \(\urcorner P\) | \(P \vee \urcorner P\) | \(P \wedge \urcorner P\) |
| T | F | T | F |
| F | T | T | F |
| \(P\) | \(Q\) | \(P \vee Q\) | \(P \to (P \vee Q)\) |
| T | T | T | T |
| T | F | T | T |
| F | T | T | T |
| F | F | F | T |
Sección 2.2
Comprobación de progreso 2.7
- A partir de la equivalencia sugerida, obtenemos
\[\begin{array} {rcl} {(P \wedge \urcorner Q) \to R} &\equiv & {\urcorner (P \wedge \urcorner Q) \vee R} \\ {} &\equiv & {(\urcorner P \vee \urcorner (\urcorner Q)) \vee R} \\ {} &\equiv & {\urcorner P \vee (Q \vee R)} \\ {} &\equiv & {P \to (Q \vee R)} \end{array}\] - Para esto,\(P\) seamos, “3 es un factor de”\(a \cdot b\), let\(Q\) be, “es un factor de”\(a\), y let\(R\) be, “3 es un factor de”\(b\). Entonces la proposición declarada se escribe en la forma\(P \to (Q \vee R)\). Ya que esto es lógicamente equivalente a\((P \wedge \urcorner Q) \to R\), si demostramos que
si 3 es un factor de\(a \cdot b\) y 3 no es un factor de\(a\), entonces 3 es un factor de\(b\), entonces hemos probado la proposición original.
Sección 2.3
Comprobación de progreso 2.9
- \(10 \in A\),\(22 \in A\),\(13 \notin A\),\(0 \in A\),\(-12 \notin A\)
- \(A = B, A \subseteq B, B \subseteq A, A \subseteq C, A \subseteq D, B \subseteq C, B \subseteq D\)
Comprobación de Progreso 2.11
- (a) Dos valores de\(x\) para los cuales\(P(x)\) es falso son\(x = 3\) y\(x = -4\).
(b) El conjunto de todos\(x\) para el que\(P(x)\) es verdadero es el conjunto {-2, -1, 0, 1, 2}. - a) Dos ejemplos para los que\(R(x, y, z)\) es falso son:\(x = 1, y = 1, z = 1\) y\(x = 3\),\(y = -1\),\(z = 5\).
b) Dos ejemplos para los que\(R(x, y, z)\) es cierto son:\(x = 3, y = 4, z = 5\) y\(x = 5, y = 12, z = 13\).
Comprobación de Progreso 2.13
- El conjunto de verdad es el conjunto de todos los números reales cuyo cuadrado es menor o igual a 9. El conjunto de la verdad es\(\{x \in \mathbb{R}\ |\ x^2 \le 9\} = \{x \in \mathbb{R}\ |\ -3 \le x \le 3\}\).
- El conjunto de verdad es el conjunto de todos los enteros cuyo cuadrado es menor o igual a 9. El conjunto de verdad es {-3, -2, -1, 0, 1, 2, 3}.
- Los conjuntos de verdad en Partes (1) y (2) iguales no son iguales. Un propósito de esta comprobación de progreso es mostrar que el conjunto de verdad de un predicado depende del predicado y del conjunto universal.
Comprobación de Progreso 2.15
\(A = \{4n - 3\ |\ n \in \mathbb{N}\} = \{x \in \mathbb{N}\ |\ x = 4n - 3 \text{ for some natural number \(n\)}\}.\)
\(B = \{-2n\ |\ \text{\(n\)es un entero no negativo\}.\)
\(C = \{(\sqrt{2})^{2m - 1}\ |\ m \in \mathbb{N}\} = \{(\sqrt{2})^n\ |\ \text{\(n\)es un número natural impar}\}.\)
\(D = \{3^n\ |\ \text{\(n\)es un entero no negativo}\}.\)
Sección 2.4
Comprobación de Progreso 2.18
- \(\bullet\)Por cada número real\(a\),\(a + 0 = a\).
\(\bullet\)\((\exists a \in \mathbb{R}) (a + 0 \ne a).\)
\(\bullet\)Existe un número real\(a\) tal que\(a + 0 \ne a\). - \(\bullet\)Por cada número real\(x\), sin (2\(x\)) = 2 (sin\(x\)) (cos\(x\)).
\(\bullet\)\((\exists x \in \mathbb{R})\)(sin (2\(x\))\(\ne\) 2 (sin\(x\)) (cos\(x\))).
\(\bullet\)Existe un número real\(x\) tal que el pecado (2\(x\))\(\ne\) 2 (pecado\(x\)) (cos\(x\)). - \(\bullet\)Por cada número real\(x\),\(\text{tan}^2 x + 1 = \text{sec}^2 x\).
\(\bullet\)\((\exists x \in \mathbb{R}) (\text{tan}^2 x + 1 \ne \text{sec}^2 x)\).
\(\bullet\)Existe un número real\(x\) tal que\(\text{tan}^2 x + 1 \ne \text{sec}^2 x\). - \(\bullet\)Existe un número racional\(x\) tal que\(x^2 - 3x - 7 = 0\).
\(\bullet\)\((\forall x \in \mathbb{Q})(x^2 - 3x - 7 \ne 0).\)
\(\bullet\)Para cada número racional\(x\),\(x^2 - 3x - 7 \ne 0\). - \(\bullet\)Existe un número real\(x\) tal que\(x^2 + 1 = 0\).
\(\bullet\)\((\forall x \in \mathbb{R})(x^2 + 1 \ne 0).\)
\(\bullet\)Por cada número real\(x\),\(x^2 + 1 \ne 0\).
Comprobación de Progreso 2.19
- Un contraejemplo es\(n = 4\) since\(4^2 + 4 + 1 = 21\), y 21 no es primo.
- Un contraejemplo es\(x = \dfrac{1}{4}\) ya que\(\dfrac{1}{4}\) es positivo y\(2(\dfrac{1}{4})^2 = \dfrac{1}{8}\) y\(\dfrac{1}{8} \le \dfrac{1}{4}\).
Comprobación de Progreso 2.20
1. Un entero\(n\) es un múltiplo de 3 siempre que\(\exists k \in \mathbb{Z})(n = 3k)\).
4. Un entero no\(n\) es un múltiplo de 3 siempre que\(\forall k \in \mathbb{Z})(n \ne 3k)\).
5. Un entero no\(n\) es un múltiplo de 3 siempre que para cada entero\(k\),\(n \ne 3k\).
Comprobación de Progreso 2.21
- \((\exists x \in \mathbb{Z})(\exists y \in \mathbb{Z}) (x + y \ne 0)\).
- Existen enteros\(x\) y\(y\) tal que\(x + y \ne 0\).
Sección 3.1
Comprobación de progreso 3.2
- Para cada ejemplo en la Parte (1), el entero\(a\) divide la suma\(b + c\).
- Conjetura: Para todos los enteros\(a\)\(b\),, y\(c\) con\(a \ne 0\), si\(a\)\(a\) divide\(b\) y divide\(c\), entonces\(a\) divide\(b + c\).
- Una tabla de Know show para una prueba de la conjetura en la Parte (3).
| Paso | Conoce | Razón |
| \(P\) | \(a\ |\ b\)y\(a\ |\ c\) | Hipótesis |
| \(P\)1 | \((\exists s \in \mathbb{Z})(b = a \cdot s)\) \((\exists t \in \mathbb{Z})(c = a \cdot t)\) |
Definición de “divide” |
| \(P\)2 | \(b + c = as + at\) | Sustituyendo\(b\) y\(c\) |
| \(P\)3 | \(b + c = a(s + t)\) | Propiedad distributiva |
| \(Q\)1 | \(s + t\)es un número entero | \(\mathbb{Z}\)se cierra bajo adición |
| \(Q\) | \(a\ |\ (b + c)\) | Definición de “divide” |
| Paso | Mostrar | Razón |
Comprobación de progreso 3.3
Un contraejemplo para esta declaración serán los valores de a y b para los cuales 5 divide\(a\) o 5 divide\(b\), y 5 no divide\(5a + b\). Un contraejemplo para la declaración es\(a = 5\) y\(b = 1\). Para estos valores, la hipótesis es cierta ya que 5 divide a y la conclusión es falsa ya que\(5a + b = 26\) 5 no divide 26.
Comprobación de progreso 3.4
- Algunos enteros que son congruentes a 5 módulo 8 son -11, -3, 5, 13 y 21.
- \(\{x \in \mathbb{Z}\ |\ x \equiv 5\text{ (mod 8)\} = \{..., -19, -11, -3, 5, 13, 21, 29, ...\}\).
- Por ejemplo, -3 + 5 = 2, -11 + 29 = 18, 13 + 21 = 34.
- Si restamos 2 de alguna de las sumas obtenidas en la Parte (3), el resultado será un múltiplo de 8. Esto quiere decir que la suma es congruente a 2 módulo 8. Por ejemplo,\(2 - 2 = 0\),\(18 - 2 = 16\),\(34 - 2 = 32\).
Comprobación de progreso 3.6
- Para probar que 8 divide\((a + b - 2)\), podemos probar que existe un entero\(q\) tal que (\(a + b - 2 = 8q\)).
- Desde 8 divide (\(a - 5\)) y (\(b - 5\)), existen enteros\(k\) y\(m\) tal que\(a - 5 - 8k\) y\(b - 5 = 8m\).
- \(a = 5 + 8k\)y\(b = 5 + 8m\).
- \(a + b - 2 = (5 + 8k) + 5 + 8m) - 2 = 8 + 8k + 8m = 8(1 + k + m)\).
- Comprobante. Que a y b sean enteros y supongamos que\(a \equiv 5\) (mod 8) y\(b \equiv 5\) (mod 8). Eso lo demostraremos\((a + b) \equiv 2\) (mod 8\). Desde 8 divide\((a - 5)\) y\((b - 5)\), existen enteros\(k\) y\(m\) tal que\(a - 5 = 8k\) y\(b - 5 = 8m\). Entonces vemos que
\[\begin{array} {a + b - 2} &= & {(5 + 8k) + (5 + 8m) - 2] \\ {} &= & {8 + 8k + 8m} \\ {} &= & {8(1 + k + m)} \end{array}\]
Por las propiedades de cierre de los enteros,\((1 + k + m)\) es un entero y así la última ecuación prueba que 8 divide (\(a + b - 2\)) y por lo tanto,\((a + b) \equiv 2\) (mod 8). Esto demuestra que si\(a \equiv 5\) (mod 8) y\(b \equiv 5\) (mod 8), entonces\((a + b) \equiv 2\) (mod 8).
Sección 3.2
Comprobación de progreso 3.8
- Para todos los números reales\(a\) y\(b\), si\(ab = 0\), entonces\(a = 0\) o\(b = 0\).
- Para todos los números reales\(a\) y\(b\), si\(ab = 0\) y\(a \ne 0\),\(b = 0\)
- Esto da Ahora
\[\dfrac{1}{a}(ab) = \dfrac{1}{a} \cdot 0.\]
usamos la propiedad asociativa en el lado izquierdo de esta ecuación y simplificamos ambos lados de la ecuación para obtener
\[\begin{array} {rcl} {(\dfrac{1}{a} \cdot a) b} &= & {0} \\ {1 \cdot b} &= & {0} \\ {b} &= & {0} \end{array}\]
Por lo tanto,\(b = 0\) y esto completa la prueba de una declaración que es lógicamente equivalente a lo contrapositivo. De ahí que hayamos probado la proposición.
Sección 3.3
Comprobación de Progreso 3.15
- Existe un número real\(x\) tal que\(x\) es irracional y\(\sqrt[3]{x}\) racional.
- Existe un número real\(x\) tal que\(x + \sqrt{2}\) es racional y\((-x + \sqrt{2})\) es racional.
- Existen enteros\(a\) y\(b\) tal que 5 divide\(ab\) y 5 no divide\(a\) y 5 no divide\(b\).
- Existen números reales\(a\) y\(b\) tal que\(a > 0\) y\(b > 0\) y\(\dfrac{2}{a} + \dfrac{2}{b} = \dfrac{4}{a + b}\).
Comprobación de Progreso 3.16
- Algunos enteros que son congruentes a 2 módulo 4 son -6. -2, 2, 6, 10, y algunos enteros que son congruentes a 3 módulo 6 son: -9, -3, 3, 9, 15. No hay números enteros que estén en ambas listas.
- Para esta proposición, es razonable probar una prueba por contradicción ya que la conclusión se afirma como una negación.
- Prueba. Usaremos una prueba por contradicción. Vamos\(n \in \mathbb{Z}\) y supongamos que\(n \equiv 2\) (mod 4) y eso\(n \equiv 3\) (mod 6). Desde\(n \equiv 2\) (mod 4), sabemos que 4 divide\(n - 2\). Por lo tanto, existe un entero\(k\) tal que
\[n - 2 = 4k.\]También podemos usar la suposición de que\(n \equiv 3\) (mod 6) para concluir que 6 divide\(n - 3\) y que existe un entero\(m\) tal que
\[n - 3 = 6m.\]
si ahora resolvemos ecuaciones (B.5) y (B.6) para n y establecemos las dos expresiones iguales entre sí, obtenemos
\[4k + 2 = 6m + 3.\]
Sin embargo, esta ecuación se puede reescribir como
\[2(2k + 1) = 2(3m + 1) + 1.\]
Dado que\(2k + 1\) es un entero y\(3m + 1\) es un entero, esta última ecuación es una contradicción ya que el lado izquierdo es un entero par y el lado derecho es un entero impar. De ahí que hayamos probado que si\(n \equiv 2\) (mod 4), entonces\(n \equiv 3\) (mod 6).
Comprobación de Progreso 3.18
- \(x^2 + y^2 = (2m + 1)^2 + (2n + 1)^2 = 2(2m^2 + 2m + 2n^2 + 2n + 1).\)
- Usando álgebra para reescribir la última ecuación, obtenemos
\[4m^2 + 4m + 4n^2 + 4n + 2 = 4k^2.\]
Si dividimos ambos lados de esta ecuación por 2, vemos eso\(2m^2 + 2m + 2n^2 + 2n + 1 = 2k^2\) o
\[2(m^2 + m + n^2 + n) + 1 = 2k^2.\]
Sin embargo, el lado izquierdo de la última ecuación es un entero impar y el lado derecho es un entero par. Esto es una contradicción, y así hemos demostrado que para todos los enteros\(x\) y\(y\), si\(x\) y\(y\) son enteros impares, entonces no existe un entero\(z\) tal que\(x^2 + y^2 = z^2\).
Sección 3.4
Comprobación de Progreso 3.21
Proposición. Para cada entero\(n\),\(n^2 - 5n + 7\) es un entero impar.
Comprobante. Dejar\(n\) ser un entero. Demostraremos que\(n^2 - 5n + 7\) es un entero impar examinando el caso donde\(n\) es par y el caso donde\(n\) es impar.
En el caso donde\(n\) es par, existe un entero m tal que\(n = 2m\). Entonces en este caso,
\(\begin{array} {rcl} {n^2 - 5n + 7} &= & {(2m^2) - 5(2m) + 7} \\ {} &= & {4m^2 - 10m + 6 + 1} \\ {} &= & {2(2m^2 - 5m + 3) + 1.} \end{array}\)
Dado que (\(2m^2 - 5m + 3\)) es un entero, la última ecuación muestra que si\(n\) es par, entonces\(n^2 - 5n + 7\) es impar.
En el caso donde\(n\) es impar, existe un entero\(m\) tal que\(n = 2m + 1\). Entonces en este caso,
\(\begin{array} {rcl} {n^2 - 5n + 7} &= & {(2m + 1)^2 - 5(2m + 1) + 7} \\ {} &= & {4m^2 - 14m + 3} \\ {} &= & {2(2m^2 - 7m + 1) + 1.} \end{array}\)
Dado que (\(2m^2 - 7m + 1\)) es un entero, la última ecuación muestra que si\(n\) es impar, entonces\(n^2 - 5n + 7\) es impar. De ahí que al usar estos dos casos, hemos demostrado que para cada entero\(n\),\(n^2 - 5n + 7\) es un entero impar.
Comprobación de Progreso 3.24
- |4.3| = 4.3 y |-\(\pi\) | =\(\pi\)
- (a)\(t = 12\) o\(t = -12\)
(b)\(t + 3 = 5\) o\(t + 3 = -5\). Entonces\(t = 2\) o\(t = -8\).
(c)\(t - 4 = \dfrac{1}{5}\) o\(t - 4 = -\dfrac{1}{5}\). Entonces\(t = \dfrac{21}{5}\) o\(t = \dfrac{19}{5}\).
d)\(3t - 4 = 8\) o\(3t - 4 = -8\). Entonces\(t = 4\) o\(t = -\dfrac{4}{3}\).
Sección 3.5
Comprobación de Progreso 3.26
- a) Los posibles restos son 0, 1, 2 y 3.
b) Los posibles restos son 0, 1, 2, 3, 4, 5, 6, 7 y 8.
a)\(17 = 5 \cdot 3 + 2\)
b\(-17 = (-6) \cdot 3 + 1\)
) c\(73 = 10 \cdot 7 + 3\)
) d\(-73 = (-11) \cdot 7 + 4\)
) e\(436 = 16 \cdot 27 + 4\)
) f\(539 = 4 \cdot 110 + 99\)
Comprobación de Progreso 3.29
Prueba. Dejar\(n\) ser un número natural y dejar\(a, b, c\) y\(d\) ser enteros. Asumimos que\(a \equiv b\) (mod\(n\)) y\(c \equiv d\) (mod\(n\)) y probaremos que\((a + c) \equiv (b + d)\) (mod\(n\)). Desde\(a \equiv b\) (mod\(n\)) y\(c \equiv d\) (mod\(n\)),\(n\) divide\(a - b\)\(c - d\) y y así existen enteros\(k\) y\(q\) tal que\(a - b = nk\) y\(c - d = nq\). Luego podemos escribir\(a = b + nk\)\(c = d + nq\) y obtener
\(\begin{array} {rcl} {a + c} &= & {(b + nk) + (d + nq)} \\ {} &= & {(b + d) + n(k + q)} \end{array}.\)
Al restar\((b + d)\) de ambos lados de la última ecuación, vemos que
\((a + c) - (b + d) = n(k + q).\)
Ya que\((k + q)\) es un entero, esto prueba que\(n\) divide\((a + c) - (b + d)\), y de ahí, podemos concluir que\((a + c) \equiv (b + d)\) (mod\(n\)).
Comprobación de Progreso 3.34
Caso 2. (\(a \equiv 2\)(mod 5)). En este caso, utilizamos el Teorema 3.28 para concluir que
\(a^2 \equiv 2^2\)(mod 5) o\(a^2 \equiv 4\) (mod 5).
Esto demuestra que si\(a \equiv 2\) (mod 5), entonces\(a^2 \equiv 4\) (mod 5).
Caso 3. (\(a \equiv 3\)(mod 5)). En este caso, utilizamos el Teorema 3.28 para concluir que
\(a^2 \equiv 3^2\)(mod 5) o\(a^2 \equiv 9\) (mod 5).
También lo sabemos\(9 \equiv 4\) (mod 5). Entonces tenemos\(a^2 \equiv 9\) (mod 5) y\(9 \equiv 4\) (mod 5), y ahora podemos usar la propiedad transitiva de congruencia (Teorema 3.30) para concluir que\(a^2 \equiv 4\) (mod 5). Esto demuestra que si\(a \equiv 3\) (mod 5), entonces\(a^2 \equiv 4\) (mod 5).
Sección 4.1
Comprobación de progreso 4.1
- No es posible saber si\(1 \in T\) y\(5 \in T\).
- Cierto.
- Cierto. El contrapositivo es, “Si\(2 \in T\), entonces”\(5 \in T\), lo cual es cierto.
- Cierto.
- Falso. Si\(k \in T\), entonces\(k + 1 \in T\).
- Es cierto, ya que “k\ notin t\) OR\(k + 1 \in T\)" es lógicamente equivalente a “Si\(k \in T\), entonces”\(k + 1 \in T\).
- No es posible saber si esto es cierto. Es lo contrario de la sentencia condicional, “Por cada entero\(k\), si\(k \in T\), entonces”\(k + 1 \in T\).
- Cierto. Este es el contrapositivo de la sentencia condicional, “Por cada entero\(k\), si\(k \in T\), entonces”\(k + 1 \in T\).
Comprobación de progreso 4.3
Prueba. \(P(n)\)Sea el predicado, "\(1 + 2 + 3 + \cdot\cdot\cdot + n = \dfrac{n(n + 1)}{2}\).” Para el paso base, observe que la ecuación\(1 = \dfrac{1(1 + 1)}{2}\) muestra que eso\(P(1)\) es cierto. Ahora vamos a\(k\) ser un número natural un asumir que\(P(k)\) es cierto. Es decir, supongamos que
\[1 + 2 + 3 + \cdot\cdot\cdot + k = \dfrac{k(k + 1)}{2}.\]
Ahora tenemos que demostrar que\(P(k + 1)\) es cierto o que
\[1 + 2 + 3 + \cdot\cdot\cdot + k + (k + 1) = \dfrac{(k + 1)(k + 2)}{2}.\]
Al\((k + 1)\) sumar a ambos lados de la ecuación (B.11), vemos que
\(\begin{array} {rcl} {1 + 2 + 3 + \cdot\cdot\cdot + k + (k + 1)} &= & {\dfrac{k(k + 1)}{2} + (k + 1)} \\ {} &= & {\dfrac{k(k + 1) + 2(k + 1)}{2}} \\ {} &= & {\dfrac{k^2 + 3k + 2}{2}} \\ {} &= & {\dfrac{(k + 1)(k + 2)}{2}.} \end{array}\)
Al comparar la última ecuación con la ecuación (2), vemos que hemos demostrado que si\(P(k)\) es verdadera, entonces\(P(k + 1)\) es verdadera, y se ha establecido el paso inductivo. De ahí que por el Principio de Inducción Matemática, hemos demostrado que para cada entero\(n\),\(1 + 2 + 3 + \cdot\cdot\cdot + n = \dfrac{n(n + 1)}{2}\).
Comprobación de Progreso 4.5
Para el paso inductivo, dejemos\(k\) ser un número natural y supongamos que eso\(P(k)\) es cierto. Es decir, supongamos que\(5^k \equiv 1\) (mod 4).
- Para probar que eso\(P(k + 1)\) es cierto, debemos probar\(5^{k + 1} \equiv 1\) (mod 4).
- Ya que\(5^{k + 1} = 5 \cdot 5^{k}\), multiplicamos ambos lados de la congruencia\(5^{k} \equiv 1\) (mod 4) por 5 y obtenemos
\[5 \cdot 5^k \equiv 5 \cdot 1 \text{ (mod 4) or}\ \ \ \ \ \ \ \ 5^{k + 1} \equiv 5 \text{ (mod 4).}\] - Desde\(5^{k + 1} \equiv 5\) (mod 4) y sabemos que\(5 \equiv 1\) (mod 4), podemos usar la propiedad transitiva de congruencia para obtener\(5^{k + 1} \equiv 1\) (mod 4). Esto demuestra que si\(P(k)\) es cierto, entonces\(P(k + 1)\) es cierto, y de ahí, por el Principio de Inducción Matemática, hemos demostrado que para cada número natural\(n\),\(5^n \equiv 1\) (mod 4).
Sección 4.2
Comprobación de progreso 4.8
- Por cada número natural\(n\), si\(n \ge 3\), entonces\(3^n > 1 + 2^n\).
- Por cada número natural\(n\), si\(n \ge 6\), entonces\(2^n > (n + 1)^2\).
- Por cada número natural\(n\), si\(n \ge 6\), entonces\((1 + \dfrac{1}{n})^n > 2.5\).
Comprobación de Progreso 4.10
Construya la siguiente tabla y utilízala para responder las dos primeras preguntas. El cuadro muestra que\(P(3)\),\(P(5)\), y\(P(6)\) son ciertos. También podemos ver eso\(P(2)\),\(P(4)\), y\(P(7)\) son falsos. También parece que si\(n \in \mathbb{N}\) y\(n \ge 8\), entonces\(P(n)\) es cierto.
| \(x\) | 0 | 1 | 2 | 3 | 4 | 0 | 1 | 2 | 0 | 1 | 1 |
| \(y\) | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 2 | 2 | 3 |
| \(3x+ 5y\) | 0 | 3 | 6 | 9 | 12 | 5 | 8 | 11 | 10 | 13 | 18 |
La siguiente proposición proporciona respuestas para Problemas (3) y (4).
Proposición 4.11. Para todos los números naturales\(n\) con\(n \ge 8\), existen enteros no negativos\(x\) y\(y\) tal que\(n = 3x + 5y\).
Comprobante. (por inducción matemática) Dejar\(\mathbb{Z}^{\ast} = \{x \in \mathbb{Z}\ |\ x \ge 0\}\), y para cada número natural\(n\), dejar\(P(n)\) ser, “existe\(x, y \in \mathbb{Z}^{\ast}\) tal que”\(n = 3x + 5y\).
Paso Base: Usando la tabla anterior, vemos que\(P(8)\),\(P(9)\), y\(P(10)\) son ciertos.
Paso Inductivo: Dejemos\(k \in \mathbb{N}\) con\(k \ge 13\). asumir que\(P(8)\)\(P(9)\),,...,\(P(k)\) son ciertos. Ahora, fíjate que
\(k + 1 = 3 + (k - 2).\)
Ya que\(k \ge 10\), podemos concluir que\(k - 2 \ge 8\) y por lo tanto\(P(k - 2)\) es cierto. Por lo tanto, existen enteros no negativos\(u\) y\(v\) tales que\(k - 2 = (3u + 5v)\). Usando esta ecuación, vemos que
\(\begin{array} {k + 1} &= & {3 + (3u + 5v)} \\ {} &= & {3(1 + u) + 5v}. \end{array}\)
De ahí que podamos concluir que eso\(P(k + 1)\) es cierto. Esto prueba que si\(P(8)\),\(P(9)\),...,\(P(k)\) son ciertas, entonces\(P(k + 1)\) es verdad. De ahí que por el Segundo Principio de Inducción Matemática, para todos los números naturales\(n\) con\(n \ge 8\), existen enteros no negativos\(x\) y\(y\) tales que\(n = 3x + 5y\).
Sección 4.3
Comprobación de Progreso 4.12
Prueba. Utilizaremos una prueba por inducción. Por cada número natural\(n\), dejamos\(P(n)\) ser,
\(f_{3n}\)es un número parejo natural.
Ya que\(f_3 = 2\), vemos que eso\(P(1)\) es cierto y esto prueba el paso base.
Para el paso inductivo, dejamos\(k\) ser un número natural y asumimos que eso\(P(k)\) es cierto. Es decir, supongamos que\(f_{3k}\) es un número parejo natural. Esto significa que existe un entero m tal que
\[f_{3k} = 2m.\]
Tenemos que demostrar que eso\(P(k + 1)\) es cierto o que\(f_{3(k + 1)}\) es parejo. Observe eso\(3(k + 1) = 3k + 3\) y, de ahí,\(f_{3(k + 1) = f_{3k + 3}\). Ahora podemos usar la fórmula de recursión para los números de Fibonacci para concluir que
\(f_{3k + 3} = f_{3k + 2} + f_{3k + 1}\).
Usando de nuevo la fórmula de recursión, obtenemos\(f_{3k + 2} = f_{3k + 1} + f_{3k}\). Armando todo esto, vemos que
\[\begin{array} {rcl} {f_{3(k + 1)}} &= & {f_{3k + 3}} \\ {} &= & {f_{3k + 2} +f_{3k + 1}} \\ {} &= & {(f_{3k + 1} + f_{3k}) + f_{3k + 1}} \\ {} &= & {2f_{3k + 1} + f_{3k}.} \end{array}\]
Ahora sustituimos la expresión para\(f_{3k}\) en la ecuación (B.14) por la ecuación (B.15). Esto da
\[\begin{array} {rcl} {f_{3(k + 1)}} &= & {2f_{3k + 1} + 2m} \\ {f_{3(k + 1)}} &= & {2(f_{3k + 1} + m)} \end{array}\]
Esta ecuación precedente muestra que\(f_{3(k + 1)}\) es parejo. De ahí que se haya demostrado que si\(P(k)\) es cierto, entonces\(P(k + 1)\) es cierto y se ha establecido el paso inductivo. Por el Principio de Inducción Matemática, esto demuestra que para cada número natural\(n\), el número Fibonacci\(f_{3n}\) es un número parejo natural.
Sección 5.1
Comprobación de progreso 5.3

Comprobación de progreso 5.4
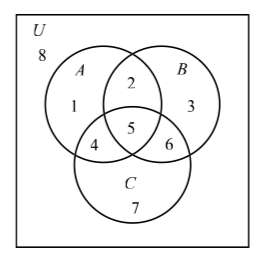
Usando el diagrama estándar de Venn para tres conjuntos que se muestran arriba:
(a) Para el conjunto\((A \cap B) \cap C\), la región 5 está sombreada.
b) Para el conjunto\((A \cap B) \cup C\), las regiones 2, 4, 5, 6, 7 están sombreadas.
(c) Para el conjunto\((A^{c} \cup B)\), las regiones 2, 3, 5, 6, 7, 8 están sombreadas.
d) Para el conjunto\((A^{c} \cap (B \cup C))\), las regiones 3, 6, 7 están sombreadas.
Sección 5.2
Comprobación de progreso 5.8
\(A = \{x \in \mathbb{Z}\ |\ x \text{ is multiple of 9}\}\)y\(B = \{x \in \mathbb{Z}\ |\ x \text{ is a multiple of 3}\}.\)
- El conjunto\(A\) es un subconjunto de\(B\). Para probarlo, dejamos\(x \in A\). Entonces existe un entero\(m\) tal que\(x = 9m\), que puede escribirse como
\[x = 3(3m).\]
Since\(3m \in \mathbb{Z}\), la última ecuación prueba que\(x\) es un múltiplo de 3 y así\(x \in B\). Por lo tanto,\(A \subseteq B\). - El conjunto no\(A\) es igual al conjunto\(B\). Tomamos nota de que\(3 \in B\) pero\(3 \notin A\). Por lo tanto,\(B \not\subseteq A\) y, de ahí,\(A \ne B\).
Comprobación de progreso 5.9
| Paso | Conoce | Razón |
| \(P\) | \(A \subseteq B\) | Hipótesis |
| \(P\)1 | Vamos\(x \in B^{c}\). | Elija un elemento arbitrario de\(B^{c}\). |
| \(P\)2 | Si\(x \in A\), entonces\(x \in B\). | Definición de “subconjunto” |
| \(P\)3 | Si\(x \notin B\), entonces\(x \notin A\). | Contrapositivo |
| \(P\)4 | Si\(x \in B^{c}\), entonces\(x \in A^{c}\). | Paso\(P\)3 and definition of “complement” |
| \(Q\)2 | El elemento\(x\) está en\(A^{c}\). | Paso\(P\) 1 y\(P\) 4 |
| \(Q\)1 | Cada elemento de\(B^{c}\) es un elemento de\(A^{c}\). | El método de escoger un elemento con Steps\(P\)1 and \(Q\)2. |
| \(Q\) | \(B^{c} \subseteq A^{c}\) | Definición de “subconjunto” |
Comprobación de Progreso 5.12
Comprobante. Dejar\(A\) y\(B\) ser subconjuntos de algún conjunto universal. Lo demostraremos\(A - B = A \cap B^{c}\) probando que cada conjunto es un subconjunto del otro conjunto. Primero lo demostraremos\(A - B \subseteq A \cap B^{c}\). Vamos\(x \in A - B\). Entonces sabemos eso\(x \in A\) y\(x \notin B\). Sin embargo, eso\(x \notin B\) implica\(x \in B^c\). De ahí,\(x \in A\) y\(x \in B^{c}\), lo que significa eso\(x \in A \cap B^{c}\). Esto lo demuestra\(A - B \subseteq A \cap B^{c}\).
Para probarlo\(A \cap B^{c} \subseteq A - B\), dejamos\(y \in A \cap B^{c}\). Esto significa que\(y \in A\) y\(y \in B^{c}\), y por lo tanto,\(y \in A\) y\(y \notin B\). Por lo tanto,\(y \in A - B\) y esto lo demuestra\(A \cap B^{c} \subseteq A - B\). Ya que hemos demostrado que cada conjunto es un subconjunto del otro conjunto, lo hemos demostrado\(A - B = A \cap B^{c}\).
Comprobación de Progreso 5.15
Comprobante. Dejar\(A = \{x \in \mathbb{Z}\ |\ x \equiv 3 \text{ (mod 12)}\}\) y\(B = \{y \in \mathbb{Z}\ |\ y \equiv 2 \text{ (mod 8)}\}\). Usaremos una prueba por contradicción para probarlo\(A \cap B = \emptyset\). Entonces asumimos eso\(A \cap B \ne \emptyset\) y vamos\(x \in A \cap B\). Entonces podemos concluir eso\(x \equiv 3 \text{ (mod 12)}\) y aquello\(x \equiv 2\) (mod 8). Esto quiere decir que existen enteros\(m\) y\(n\) tal que
\(x = 3 + 12m\)y\(x = 2 + 8n\).
Al igualar estas dos expresiones para\(x\), obtenemos\(3 + 12m = 2 + 8n\), y esta ecuación se puede reescribir como\(1 = 8n - 12m\). Esto es una contradicción ya que 1 es un entero impar y\(8n - 12m\) es un entero par. Por lo tanto, eso lo hemos demostrado\(A \cap B = \emptyset\).
Sección 5.3
Comprobación de Progreso 5.19
- En nuestra configuración estándar para un diagrama de Venn con tres conjuntos, las regiones 1, 2, 4, 5 y 6 son las regiones sombreadas para ambos\(A \cup (B \cap C)\) y\((A \cup B) \cap (A \cup C)\).
- A partir de los diagramas de Venn en la Parte (1), parece que\(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\).
Comprobación de Progreso 5.21
- Usando nuestra configuración estándar para un diagrama de Venn con tres conjuntos, las regiones 1, 2 y 3 son las regiones sombreadas para ambos\((A \cup B) - C\) y\((A - C) \cup (B- C)\).
- \(\begin{array} {rclcr} {(A \cup B) - C} &= & {(A \cup B) \cap C^{c}} & & {\text{(Theorem 5.20)}} \\ {} &= & {C^{c} \cap (A \cup B)} & & {\text{(Commutative Property)}} \\ {} &= & {(C^{c} \cap A) \cup (C^{c} \cap B)} & & {\text{(Distributive Property)}} \\ {} &= & {(A \cap C^{c}) \cup (B \cap C^{c})} & & {\text{(Commutative Property)}} \\ {} &= & {(A - C) \cup (B - C)} & & {\text{(Theorem 5.20)}} \end{array}\)
Sección 5.4
Comprobación de Progreso 5.23
- Vamos\(A = \{1, 2, 3\}\),\(T = \{1, 2\}\),\(B = \{a, b\}\), y\(C = \{a, c\}\).
(a)\(A \times B = \{(1, a), (1, b), (2, a), (2, b), (3, a), (3, b)\}\)
(b)\(T \times B = \{(1, a), (1, b), (2, a), (2, b)\}\)
(c)\(A \times C = \{(1, a), (1, c), (2, a), (2, c), (3, a), (3, c)\}\)
(d)\(A \times (B \cap C) = \{(1, a), (2, a), (3, a)\}\)
(e)\((A \times B) \cap (A \times C) = \{(1, a), (2, a), (3, a)\}\)
(f)\(A \times (B \cup C) = \{(1, a), (1, b), (1, c), (2, a), (2, b), (2, c), (3, a), (3, b), (3, c)\}\)
(g)\((A \times B) \cup (A \times C) = \{(1, a), (1, b), (1, c), (2, a), (2, b), (2, c), (3, a), (3, b), (3, c)\}\)
(h)\(A \times (B - C) = \{(1, b), (2, b), (3, b)\}\)
(i)\((A \times B) - (A \times C) = \{(1, b), (2, b), (3, b)\}\)
(j)\(B \times A = \{(a, 1), (b, 1), (a, 2), (b, 2), (a, 3), (b, 3)\}\) - \(\begin{array} {lcl} {T \times B \subseteq A \times B} & & {A \times (B \cup C) = (A \times B) \cup (A \times C)} \\ {A \times (B \cap C) = (A \times B) \cap (A \times C)} & & {A \times (B - C) = (A \times B) - (A \times C)} \end{array}\)
Comprobación de Progreso 5.24
- (a)\(A \times B = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ 0 \le x \le 2 \text{ and } 2 \le y < 4\}\)
(b)\(T \times B = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ 1 < x < 2 \text{ and } 2 \le y < 4\}\)
(c)\(A \times C = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ 0 \le x \le 2 \text{ and } 3 < y \le 6\}\)
(d)\(A \times (B \cap C) = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ 0 \le x \le 2 \text{ and } 3 < y < 4\}\)
(e)\((A \times B) \cap (A \times C) = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ 0 \le x \le 2 \text{ and } 3 < y < 4\}\)
(f)\(A \times (B \cup C) = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ 0 \le x \le 2 \text{ and } 2 \le y \le 5\}\)
(g)\((A \times B) \cup (A \times C) = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ 0 \le x \le 2 \text{ and } 2 \le y \le 5\}\)
(h)\(A \times (B - C) = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ 0 \le x \le 2 \text{ and } 2 \le y \le 3\}\)
(i)\((A \times B) - (A \times C) = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ 0 \le x \le 2 \text{ and } 2 \le y \le 3\}\)
(j)\(B \times A = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ 2 \le x <4 \text{ and } 0 \le y \le 2\}\) - \(T \times B \subseteq A \times B\)
\(A \times (B \cap C) = (A \times C) \cap (A \times C)\)
\(A \times (B \cup C) = (A \times C) \cup (A \times C)\)
\(A \times (B - C) = (A \times C) - (A \times C)\)
Sección 5.5
Comprobación de Progreso 5.26
- \(\bigcup_{j = 1}^{6} A_j = \{1, 2, 3, 4, 5, 6, 9, 16, 25, 36\}\)
- \(\bigcap_{j = 1}^{6} A_j = \{1\}\)
- \(\bigcup_{j = 3}^{6} A_j = \{3, 4, 5, 6, 9, 16, 25, 36\}\)
- \(\bigcap_{j = 3}^{6} A_j = \{1\}\)
- \(\bigcup_{j = 1}^{\infty} A_j = \mathbb{N}\)
- \(\bigcap_{j = 1}^{\infty} A_j = \{1\}\)
Comprobación de Progreso 5.27
- \(A_{1} = \{7, 14\}\),\(A_{2} = \{10, 12\}\),\(A_{3} = \{10, 12\}\),\(A_{4} = \{8, 14\}\).
- El enunciado es falso. Por ejemplo,\(2 \ne 3\) y\(A_2 = A_3\).
- El enunciado es falso. Por ejemplo,\(1 \ne -1\) y\(B_1 = B_{-1}\).
Comprobación de Progreso 5.29
- Ya que\(\bigcup_{\alpha \in \mathbb{R}^{+}} A_{\alpha} = (-1, \infty)\),\((\bigcup_{\alpha \in \mathbb{R}^{+}} A_{\alpha})^{c} = (-\infty, 1]\).
- \(\bigcap_{\alpha \in \mathbb{R}^{+}} A_{\alpha}^{c} = (-\infty, -1]\).
- Ya que\(\bigcap_{\alpha \in \mathbb{R}^{+}} A_{\alpha} = (-1, 0]\),\((\bigcap_{\alpha \in \mathbb{R}^{+}} A_{\alpha})^{c} = (-\infty, 1] \cup (0, \infty)\).
- \(\bigcup_{\alpha \in \mathbb{R}^{+}} A_{\alpha}^{c} = (-\infty, -1] \cup (0, \infty)\).
Comprobación de Progreso 5.32
Las tres familias de conjuntos (\(\mathcal{A}\),\(\mathcal{B}\), y\(\mathcal{C}\) son familias disjuntas de conjuntos. Uno, la familia\(\mathcal{A}\) es una familia disjunta de conjuntos por pares.
Sección 6.1
Comprobación de progreso 6.1
- \(f(-3) = 24\)
\(f(\sqrt{8}) = 8 - 5\sqrt{8}\) - \(g(2) = -6, g(-2) = 14\)
- {-1, 6}
- {-1, 6}
- \(\{\dfrac{5 + \sqrt{33}}{2}, \dfrac{5 - \sqrt{33}}{2}\}\)
- \(\emptyset\)
Comprobación de progreso 6.2
- (a) El dominio de la función\(f\) es el conjunto de todas las personas.
(b) Un codominio para la función\(f\) es el conjunto de todos los días en un año bisiesto.
(c) Esto significa que el rango de la función\(f\) es igual a su codominio. - (a) El dominio de la función\(s\) es el conjunto de números naturales.
(b) Un codominio para la función\(s\) es el conjunto de números naturales.
(c) Esto significa que el rango de no\(s\) es igual al conjunto de números naturales.
Comprobación de progreso 6.3
- \(f(-1) \thickapprox -3\)y\(f(2) \thickapprox -2.5\).
- Los valores\(x\) para los cuales\(f(x) = 2\) son aproximadamente -2.8, -1.9, 0.3, 1.2 y 3.5.
- El rango de\(f\) parece ser el intervalo cerrado [-3.2, 3.2] o\(\{y \in \mathbb{R}\ |\ -3.2 \le y \le 3.2\}\).
Comprobación de progreso 6.4
Solo el diagrama de flechas en la Figura (a) se puede utilizar para representar una función de\(A\) a\(B\). El rango de esta función es el conjunto\(\{a, b\}\).
Sección 6.2
Comprobación de progreso 6.5
- \(f(0) = 0\),\(f(1) = 1\),\(f(2) = 1\),\(f(3) = 1\),\(f(4) = 1\).
- \(g(0) = 0\),\(g(1) = 1\),\(g(2) = 2\),\(g(3) = 3\),\(g(4) = 4\).
Comprobación de progreso 6.6
\(I_{\mathbb{Z}_5} \ne f\)y\(I_{\mathbb{Z}_5} = g\)
Comprobación de progreso 6.7
- 3.5
- 4.02
- \(\dfrac{\pi + \sqrt{2}{4}\)
- El proceso de encontrar el promedio de un conjunto finito de números reales puede considerarse como una función de\(\mathcal{F}(\mathbb{R})\) a\(\mathbb{R}\). Entonces el dominio es\(\mathcal{F}(\mathbb{R})\), el codominio es\(\mathbb{R}\), y podemos definir una función avg: de la\(\mathcal{F}(\mathbb{R}) \to \mathbb{R}\) siguiente manera: Si\(A \in \mathcal{F}(\mathbb{R})\) y\(A = \{a_1, a_2, ..., a_n\}\), luego ave\((A) = \dfrac{a_1 + a_2 + \cdot\cdot\cdot a_n}{n}\).
Comprobación de progreso 6.8
- El sexto término es\(\dfrac{1}{18}\) y el décimo término lo es\(\dfrac{1}{30}\).
- El sexto término es\(\dfrac{1}{36}\) y el décimo término lo es\(\dfrac{1}{100}\).
- El sexto término es 1 y el décimo término es 1.
Comprobación de progreso 6.9
- \(g(0, 3) = -3\);\(g(3, -2) = 11\);\(g(-3, -2) = 11\);\(g(7, -1) = 50\).
- \(\{(m, n) \in \mathbb{Z} \times \mathbb{Z}\ |\ n = m^2\}\)
- \(\{(m, n) \in \mathbb{Z} \times \mathbb{Z}\ |\ n = m^2 - 5\}\)
Sección 6.3
Comprobación de Progreso 6.10
Las funciones\(k\),\(F\), y\(s\) son inyecciones. Las funciones\(f\) y no\(h\) son inyecciones.
Comprobación de Progreso 6.11
Las funciones\(f\) y\(s\) son las sobrejecciones. Las funciones\(k\) y no\(F\) son sobreyecciones.
Comprobación de Progreso 6.15
La función\(f\) es una inyección pero no una sobreyección. Para ver que se trata de una inyección, vamos\(a, b \in \mathbb{R}\) y asumamos eso\(f(a) = f(b)\). Esto implica que\(e^{-a} = e^{-b}\). Ahora usa la función de logaritmo natural para demostrarlo\(a = b\). Ya que\(e^{-x} > 0\) para cada número real\(x\), no hay\(x \in \mathbb{R}\) tal que\(f(x) = -1\). Entonces no\(f\) es una sobrejección.
La función\(g\) es una inyección y es una sobreyección. La prueba de que g es una inyección es básicamente la misma que la prueba que\(f\) es una inyección. Para probar que g es una sobrejección, vamos\(b \in R_{+}\). Para construir el número real a tal que g.a/ D b, resuelva la ecuación\(e^{-a} = b\) para\(a\). La solución es\(a = -\text{ln}b\). Entonces se puede verificar eso\(g(a) = b\).
Comprobación de Progreso 6.16
- Hay varios pares ordenados de\((a, b) \in \mathbb{R} \times \mathbb{R}\) tal manera que\(g(a, b) = 2\). Por ejemplo,\(g(0, 2) = 2\),\(g(-1, 4) = 2\), y\(g(2, -2) = 2\).
- Para cada uno\(z \in \mathbb{R}\),\(g(0, z) = z\).
- La parte (1) implica que la función no\(g\) es una inyección. La parte (2) implica que la función\(g\) es una sobreyección ya que para cada uno\(z \in \mathbb{R}\), (\(0, z\)) está en el dominio de\(g\) y\(g(0, z) = z\).
Sección 6.4
Comprobación de Progreso 6.17
El diagrama de flechas para\(g \circ f: A \to B\) debe mostrar lo siguiente:
\(\begin{array} {rclcrcl} {(g \circ f)(a)} &= & {g(f(a))} & & {(g \circ f)(b)} &= & {g(f(b))} \\ {} &= & {g(2) = 1} & & {} &= & {g(3) = 2} \\ {(g \circ f)(c)} &= & {g(f(c))} & & {(g \circ f)(d)} &= & {g(f(d))} \\ {} &= & {g(1) = 3} & & {} &= & {g(2) = 1} \end{array}\)
El diagrama de flechas para\(g \circ g: B \to B\) debe mostrar lo siguiente:
\(\begin{array} {rclcrcl} {(g \circ f)(1)} &= & {g(g(1))} & & {(g \circ g)(2)} &= & {g(g(2))} \\ {} &= & {g(3) = 2} & & {} &= & {g(1) = 3} \\ {(g \circ g)(3)} &= & {g(g(3))} & & {} & & {g(f(d))} \\ {} &= & {g(2) = 1} & & {} & & {} \end{array}\)
Comprobación de Progreso 6.18
- \(F = g \circ f\), donde\(f: \mathbb{R} \to \mathbb{R}\) por\(f(x) = x^2 + 3\), y\(g: \mathbb{R} \to \mathbb{R}\) por\(g(x) = x^3\).
- \(G = h \circ f\), donde\(f: \mathbb{R} \to \mathbb{R}^{+}\) por\(f(x) = x^2 + 3\), y\(h: \mathbb{R}^{+} \to \mathbb{R}\) por\(h(x) = \text{In}x\).
- \(f = g \circ k\), donde\(k: \mathbb{R} \to \mathbb{R}\) por\(k(x) = x^2 - 3\), y\(g: \mathbb{R} \to \mathbb{R}\) por\(g(x) = |x|\).
- \(g = h \circ f\), donde\(f: \mathbb{R} \to \mathbb{R}\) por\(f(x) = \dfrac{2x - 3}{x^2 + 1}\), y\(h: \mathbb{R} \to \mathbb{R}\) por\(h(x) = \text{cos} x\).
Comprobación de Progreso 6.19
Para los ejemplos que se construyen:
- \(g \circ f\)debe ser una inyección.
- \(g \circ f\)debería ser una sobrejección.
- \(g \circ f\)debe ser una biyección.
Sección 6.5
Comprobación de Progreso 6.23
Ninguno de los dos conjuntos se puede utilizar para definir una función.
1. El conjunto\(F\) no satisface la primera condición del Teorema 6.22.
2. El conjunto\(G\) no satisface la segunda condición del Teorema 6.22.
Comprobación de Progreso 6.24
2. \(f^{-1} = \{(r, a), (p, b), (q, c)\}\)
\(h^{-1} = \{(p, a), (q, b), (r, c), (q, d)\}\)
\(g^{-1} = \{(p, a), (q, b), (p, c)\}\)
3. (a)\(f^{-1}\) es una función de\(C\) a\(A\).
b) no\(g^{-1}\) es una función desde\(C\) hasta\(A\) desde\((p, a) \in g^{-1}\) y\((p, c) \in g^{-1}\).
(c) no\(h^{-1}\) es una función desde\(C\) hasta\(B\) desde\((q, b) \in h^{-1}\) y\((q, d) \in h^{-1}\).
5. Para que la inversa de una función\(F: S \to T\) sea una función de\(T\) a\(S\), la función\(F\) debe ser una biyección.
Sección 6.6
Comprobación de Progreso 6.30
- \(f(A) = \{s, t\}\)
- \(f(B) = \{f(x) \ |\ x \in b\} = \{x\}\)
- \(f^{-1}(C) = \{x \in S\ |\ f(x) \in C\} = \{a, b, c, d\}\)
- \(f^{-1}(D) = \{x \in S\ |\ f(x) \in D\} = \{a, d\}\)
Comprobación de Progreso 6.32
- \(f(0) = 2\)\(f(2) = 6\)\(f(4) = 2\)\(f(6) = 6\)
\(f(1) = 3\)\(f(3) = 3\)\(f(5) = 3\)\(f(7) = 3\) - (a)\(f(A) = \{2, 3, 6\}\)\(f^{-1}(C) = \{0, 1, 3, 4, 5, 7\}\)
\(f(B) = \{2, 3, 6\}\)\(f^{-1}(D) = \{1, 3, 5, 7\}\) - (a)\(f(A) \cap f(B) = \{2\}\)\(f(A) \cap f(B) = \{2, 3, 6\}\)
Así que en este caso,\(f(A \cap B) \subseteq f(A) \cap f(B)\).
b)\(f(A) \cup f(B) = \{2, 3, 6\}\)\(f(A \cup B) = \{2, 3, 6\}\)
Así que en este caso,\(f(A \cap B) \subseteq f(A \cup B)\).
c)\(f^{-1}(C) \cap f^{-1}(D) = f^{-1}(C \cap D) = \{1, 3, 5, 7\}\). Entonces en este caso,\(f^{-1}(C \cap D) = f^{-1}(C) \cap f^{-1}(D)\).
d)\(f^{-1}(C) \cup f^{-1}(D) = f^{-1}(C \cup D) = \{0, 1, 3, 4, 5, 7\}\). Entonces en este caso,\(f^{-1}(C \cup D) = f^{-1}(C) \cup f^{-1}(D)\). - \(f(A) = \{2, 3, 6\}\). De ahí,\(f^{-1}(f(A)) = \{0, 1, 2, 3, 4, 5, 6, 7\}\). Entonces en este caso,\(A \subseteq f^{-1}(f(A))\).
Sección 7.1
Comprobación de progreso 7.2
- (a)\(T\) es una relación sobre\(\mathbb{R}\) ya que\(S\) es un subconjunto de\(\mathbb{R} \times \mathbb{R}\).
b) Resolver la ecuación\(x^2 + 4^2 = 64\). Esto da\(x = \pm \sqrt 48\).
Resuelve la ecuación\(x^2 + 9^2 = 64\). No hay soluciones de números reales. Entonces no existe\(x \in \mathbb{R}\) tal eso\((x, 9) \in S\).
(c)\((T) = \{x \in \mathbb{R}\ |\ -8 \le x \le 8\}\) rango dom\((T) = \{y \in \mathbb{R}\ |\ -8 \le y \le 8\}\)
(d) La gráfica es un círculo de radio 8 cuyo centro está en el origen. - (a)\(R\) es una relación sobre\(A\) ya que\(R\) es un subconjunto de\(A \times A\).
(b) Si asumimos que cada estado, excepto Hawai, tiene una frontera terrestre en común consigo mismo, entonces el dominio y el rango de\(R\) son el conjunto de todos los estados excepto Hawai. Si no hacemos esta suposición, entonces el dominio y el rango son el conjunto de todos los estados excepto Hawai y Alaska.
c) La primera afirmación es verdadera. Si x tiene una frontera terrestre con y, entonces y tiene una frontera terrestre con x. La segunda declaración es falsa. A continuación se presenta un contraejemplo: (Michigan, Indiana)\(\in R\), (Indiana, Illinois)\(\in R\), pero (Michigan, Illinois)\(\notin R\).
Comprobación de progreso 7.3
- El dominio de la relación divide es el conjunto de todos los enteros distintos de cero. El rango de la relación divide es el conjunto de todos los enteros.
- (a) Esta afirmación es cierta ya que para cada uno\(a \in \mathbb{Z}\),\(a = a\cdot 1\).
(b) Esta afirmación es falsa: Por ejemplo, 2 divide 4 pero 4 no divide 2.
(c) Esta afirmación es cierta por el Teorema 3.1 en la página 88.
Comprobación de progreso 7.4
- Cada elemento en el conjunto\(F\) es un par ordenado de la forma\((x, y)\) donde\(y = x^2\).
- a)\(A = \{-2, 2\}\)
b)\(B = \{-\sqrt{10}, \sqrt{10}\}\)
c)\(C = \{25\}\)
d)\(D = \{9\}\) - La gráfica de\(y = x^2\) es una parábola con vértice en el origen que es cóncava hacia arriba.
Comprobación de progreso 7.5
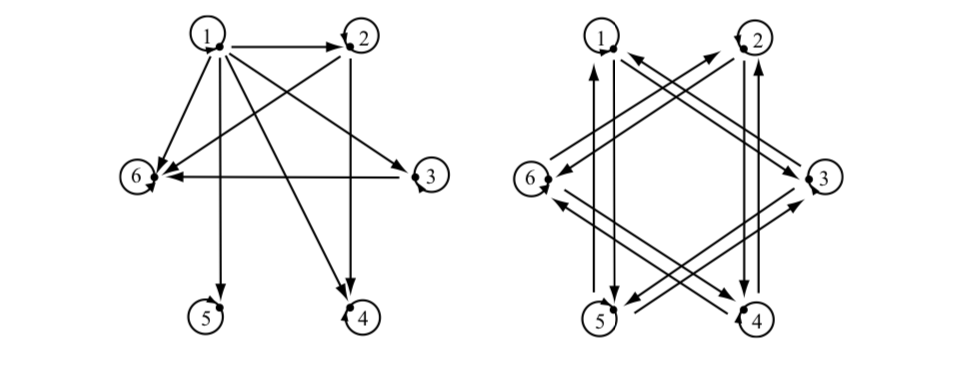
La gráfica dirigida para la Parte (a) está a la izquierda y la gráfica dirigida para la Parte (b) está a la derecha.
Sección 7.2
Comprobación de progreso 7.7
La relación\(R\):
- No es reflexivo desde\((c, c) \notin R\) y\((d, d) \notin R\).
- Es simétrico.
- No es transitivo. Por ejemplo,\((c, a) \in R\),\((a, c) \in R\), pero\((c, c) \notin R\).
Comprobación de progreso 7.9
- Prueba de que la relación\(\sim\) es simétrica: Dejemos\(a, b \in \mathbb{Q}\) y asumamos eso\(a \sim b\). Esto significa que\(a - b \in \mathbb{Z}\). Por lo tanto,\(-(a - b) \in \mathbb{Z}\) y esto significa que\(b - a \in \mathbb{Z}\), y por lo tanto,\(b \sim a\).
- Prueba de que la relación\(\sim\) es transitiva: Dejar\(a, b, c \in \mathbb{Q}\) y asumir que\(a \sim b\) y\(b \sim c\). Esto significa eso\(a - b \in \mathbb{Z}\) y aquello\(b - c \in \mathbb{Z}\). Por lo tanto,\(((a - b) + (b - c)) \in \mathbb{Z}\) y esto significa que\(a - c \in \mathbb{Z}\), y por lo tanto,\(a \sim c\).
Comprobación de Progreso 7.11
La relación\(\thickapprox\) es reflexiva\(\mathcal{P}(U)\) ya que para todos\(A \in \mathcal{P}(U)\), card (\(A\)) = card (\(A\)).
La relación\(\thickapprox\) es simétrica ya que para todos\(A, B \in \mathcal{P}(U)\), si card (\(A\)) = card (\(B\)), entonces usando el hecho de que la igualdad on\(\mathbb{Z}\) es simétrica, concluimos que card (\(B\)) = card (\(A\)). Es decir, si\(A\) tiene el mismo número de elementos que\(B\), entonces\(B\) tiene el mismo número de elementos que\(A\).
La relación\(\thickapprox\) es transitiva ya que para todos\(A, B, C \in \mathcal{P}(U)\), si card (\(A\)) = card (\(B\)) y card (\(B\)) = card (\(C\)), entonces usando el hecho de que la igualdad on\(\mathbb{Z}\) es transitiva, concluimos que card (\(A\)) = card (\(C\)). Es decir, si\(A\) y\(B\) tienen el mismo número de elementos y\(B\) y\(C\) tienen el mismo número de elementos, entonces\(A\) y\(C\) tienen el mismo número de elementos.
Por lo tanto, la relación\(\thickapprox\) es una relación de equivalencia sobre\(\mathcal{P}(U)\).
Sección 7.3
Comprobación de Progreso 7.12
Las distintas clases de equivalencia para la relación\(R\) son:\(\{a, b, e\}\) y\(\{c, d\}\).
Comprobación de Progreso 7.13
Las distintas clases de congruencia para el módulo de congruencia 4 son
[0] = {..., -12, -8, -4, 0, 4, 8, 12, ... } [1] = {..., -11, -7, -3, 1, 5, 9, 13,...}
[2] = {..., -10, -6, -2, 2, 6, 10, 14, ... } [1] = {..., -9, -5, -1, 3, 7, 11, 15,...}
Comprobación de Progreso 7.15
- [5] = [-5] = {-5, 5} [\(\pi\)] = [-\(\pi\)] = {-\(\pi\),\(\pi\)}
[10] = [-10] = {-10, 10} - [0] = {0}
- [\(a\)] = {-\(a\),\(a\)}
Sección 7.4
Comprobación de progreso 7.2
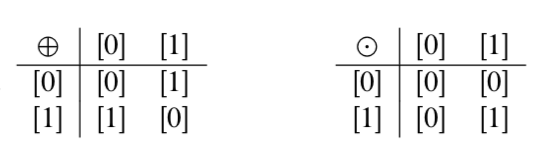
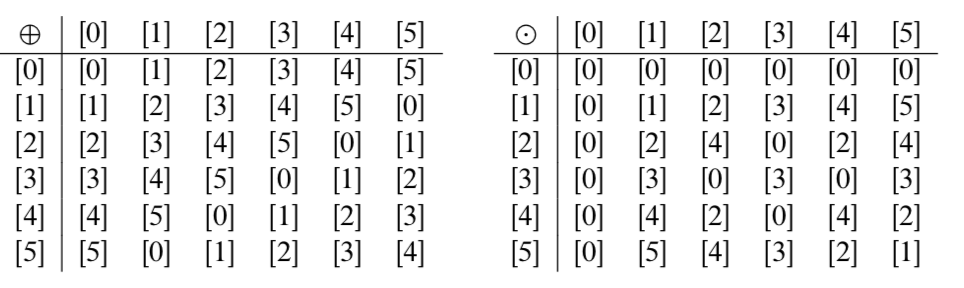
- Para todos\(a, b \in \mathbb{Z}\), si\(a \ne 0\) y\(b \ne 0\), entonces\(ab \ne 0\).
- El enunciado en (a) es verdadero y el enunciado en (b) es falso. Por ejemplo, en\(\mathbb{Z}_{6}\),\([2] \odot [3] = [0]\).
Sección 8.1
Comprobación de progreso 8.2
- El resto es 8.
- gcd (12, 8) = 4
- \(12 = 8 \cdot 1 + 4\)y gcd (\(r\),\(r_2\)) = gcd (8, 4) = 4.
Comprobación de Progreso 8.4
-
Par Original Ecuación del algoritmo de división Nuevo par (180, 126) \(180 = 126 \cdot 1 + 54\) (126, 54) (126, 54) \(126 = 54 \cdot 2 + 18\) (54, 18) (54, 18) \(54 = 18 \cdot 3 + 0\) En consecuencia, gcd (180, 126) = 18.
-
Par Original Ecuación del algoritmo de división Nuevo par (4208, 288) \(4208 = 288 \cdot 14 + 176\) (288, 176) (288, 176) \(288 = 126 \cdot 1+ 112\) (176, 112) (176, 112) \(176 = 112 \cdot 1+ 64\) (112, 64) (112, 64) \(112 = 64 \cdot 1+ 48\) (64, 48) (64, 48) \(64 = 48 \cdot 1+ 16\) (48, 16) (48, 16) \(48 = 16 \cdot 3+ 0\) En consecuencia, gcd (4208. 288) = 16.
Comprobación de Progreso 8.7
- De la comprobación de progreso 8.4, gcd (180, 126) = 18.
\[\begin{array}{rcl} {18} &= & {126 - 54 \cdot 2} \\ {} &= & {126 - (180 - 126) \cdot 2} \\ {} &= & {126 \cdot 3 + 180 \cdot (-2)} \end{array}\]
Entonces gcd (180, 126) = 18, y\(18 = 126 \cdot 3 + 180 \cdot (-2)\). - De Comprobación de Progreso 8.4, gcd (4208. 288) = 16.
\[\begin{array}{rcl} {16} &= & {64 - 48} \\ {} &= & {64 - (112 - 64) = 64 \cdot 2 - 112} \\ {} &= & {(176 - 112) \cdot 2 - 112 = 176 \cdot 2 - 112 \cdot 3} {} &= & {176 \cdot 2 - (288 - 176) \cdot 3 = 176 \cdot 5 - 288 \cdot 3} \\ {} &= & {(4208 - 288 \cdot 14) \cdot 5 - 288 \cdot 3} \\ {} &= & {4208 \cdot 5 + 288 \cdot (-73)} \end{array}\]
Entonces gcd (4208. 288) = 16, y\(16 = 4208 \cdot 5 + 288 \cdot (-73)\).
Sección 8.2
Comprobación de Progreso 8.10
- Si\(a, p \in \mathbb{Z}\),\(p\) es primo, y\(p\) divide\(a\), entonces gcd (\(a\),\(p\)) =\(p\).
- Si\(a, p \in \mathbb{Z}\),\(p\) es primo, y\(p\) no divide\(a\), entonces gcd (\(a\),\(p\)) = 1.
- Tres ejemplos son gcd (4, 9) = 1, gcd (15, 16) = 1, gcd (8, 25) = 1.
Comprobación de Progreso 8.13
Teorema 8.12. Dejar\(a\),\(b\), y\(c\) ser enteros. Si\(a\) y\(b\) son relativamente primos y\(a\ |\ (bc)\). Vamos a probar que\(a\) divide\(c\).
Prueba. Dejar\(a\),\(b\), y\(c\) ser enteros. Supongamos que\(a\) y\(b\) son relativamente primos y\(a\ |\ (bc)\). Vamos a probar que\(a\) divide\(c\).
Desde\(a\) divide\(bc\), existe un entero\(k\) tal que
\[bc = ak.\]
Además, estamos asumiendo que\(a\) y\(b\) son relativamente primos y por lo tanto gcd (\(a\),\(b\)) = 1. Así que por el Teorema 8.9, existen enteros\(m\) y\(n\) tal que
\[am + bn = 1.\]
Ahora multiplicamos ambos lados de la ecuación (B.21) por\(c\). Esto da
\[\begin{array} {rcl} {(am + bn)c} &= & {1 \cdot c} \\ {acm + bcn} &= & {c} \end{array}\]
Ahora podemos usar la ecuación (B.20) para sustituir\(bc = ak\) en la ecuación (B.22) y obtener
\(acm + akn = c.\)
Si ahora factorizamos el lado izquierdo de esta última ecuación, eso lo vemos\(a(cm + kn) = c\). Dado que (\(cm + kn\)) es un entero, esto prueba que\(a\) divide\(c\). De ahí que hayamos demostrado que si a y b son relativamente primos y\(a\ |\ (bc)\), entonces\(a\ |\ c\).
Sección 8.3
Comprobación de Progreso 8.20
2. \(x = 2 + 3k\)y\(y = 0 - 2k\), donde\(k\) puede ser cualquier entero. Nuevamente, esto no prueba que estas sean las únicas soluciones.
Comprobación de Progreso 8.21
Una de las ecuaciones Diofantinas en la Actividad Previa 2 fue\(3x + 5y = 11\). Pudimos escribir las soluciones de esta ecuación Diofantina en la forma
\(x = 2 + 5k\)y\(y = 1 - 3k\),
donde\(k\) es un entero. Observe que\(x = 2\) y\(y = 1\) es una solución de esta ecuación. Si consideramos que esta ecuación está en la forma\(ax + by = c\), entonces vemos que\(a = 3\),\(b = 5\), y\(c = 11\). Las soluciones para esta ecuación se pueden escribir en la forma
\(x = 2 + bk\)y\(y = 1 - ak\),
donde\(k\) es un entero.
La otra ecuación fue\(4x + 6y = 16\). Entonces en este caso,\(a = 4\),\(b = 6\), y\(c = 16\). También fíjese en eso\(d = \text{gcd}(4, 6) = 2\). Observamos que\(x = 4\) y\(y = 0\) es una solución de esta ecuación diofantina y las soluciones se pueden escribir en la forma
\(x = 4 + 3k\)y\(y = 0 - 2k\),
donde\(k\) es un entero. Usando los valores de\(a\),\(b\), y\(d\) dados anteriormente, vemos que las soluciones se pueden escribir en la forma
\(x = 2 + \dfrac{b}{d}k\)y\(y = 0 - \dfrac{a}{d}\),
donde\(k\) es un entero.
Comprobación de Progreso 8.24
- Ya que 21 no divide 40, el Teorema 8.22 nos dice que la ecuación Diofantina no\(63x + 336y = 40\) tiene soluciones. Recuerde que esto significa que no hay un par ordenado de enteros (\(x\),\(y\)) tal que\(63x + 336y = 40\). No obstante, si permitimos\(x\) y\(y\) seamos números reales, entonces hay soluciones de números reales. De hecho, podemos graficar la línea recta cuya ecuación está\(63x + 336y = 40\) en el plano cartesiano. Del hecho de que no hay par de enteros\(x\),\(y\) tal que\(63x + 336y = 40\), podemos concluir que no hay punto en la gráfica de esta línea en el que ambas coordenadas sean números enteros.
- Para escribir fórmulas que generen todas las soluciones, primero necesitamos encontrar una solución para\(144x + 225y = 27\). Esto a veces se puede hacer por ensayo y error, pero hay una manera sistemática de encontrar una solución. El primer paso es utilizar el Algoritmo Euclidiana a la inversa para escribir gcd (144, 225) como una combinación lineal de 144 y 225. Consulte la Sección 8.1 para revisar cómo hacer esto. El resultado de usar el Algoritmo Euclideano a la inversa para esta situación es
\[144 \cdot 11 + 225 \cdot (-7) = 9.\]
Si multiplicamos ambos lados de esta ecuación por 3, obtenemos
\[144 \cdot 33 + 225 \cdot (-21) = 27.\]
Esto quiere decir que\(x_0 = 33\),\(y_0 = -21\) es una solución de lo lineal Ecuación diofantina\(144x + 225y = 27\). Ahora podemos usar el Teorema 8.22 para concluir que todas las soluciones de esta ecuación diofantina se pueden escribir en la forma
\[x = 33 + \dfrac{225}{9}k\ \ \ \ \ \ \ \ \ y = -21 - \dfrac{144}{9}k,\]
donde\(k \in \mathbb{Z}\).
Comprobamos esta solución general de la siguiente manera: Vamos\(k \in \mathbb{Z}\). Entonces
\[\begin{array} {rcl} {144x + 225y} &= & {144(33 + 25k) + 225(-21 - 16k)} \\ {} &= & {(4752 + 3600k) + (-4725 - 3600k)} \\ {} &= & {27.} \end{array}\]
Sección 9.1
Comprobación de progreso 9.2
- Primero probamos que\(f: A \to B\) es una inyección. Así que vamos\(x, y \in A\) y asumamos eso\(f(x) = f(y)\). Entonces\(x + 350 = y + 350\) y podemos concluir eso\(x = y\). De ahí,\(f\) es una inyección. Para probar que eso\(f\) es una sobrejección, vamos\(b \in B\). Entonces\(351 \le b \le 450\) y por lo tanto,\(1 \le b - 350 \le 100\) y así\(b - 350 \in A\). En adicion,\(f(b - 350) = (b - 350) + 350 = b\). Esto demuestra que\(f\) es una sobreyección, de ahí que la función\(f\) sea una biyección, y así,\(A \thickapprox B\).
- Si\(x\) y\(t\) son pares enteros y\(F(x) = F(t)\), entonces\(x + 1 = t + 1\) y, por lo tanto,\(x = t\). Por lo tanto,\(F\) es una inyección.
Para probar que eso\(F\) es una sobrejección, vamos\(y \in D\). Esto significa que\(y\) es un número entero impar y, por lo tanto,\(y - 1\) es un número entero par. Además,
\[F(y - 1) = (y - 1 + 1 = y.\]
Por lo tanto,\(F\) es una sobreyección y por lo tanto,\(F\) es una biyección. Concluimos que\(E \thickapprox D\). - Dejemos\(x, t \in (0,1)\) y asumamos eso\(f(x) = f(t)\). Entonces\(bx = bt\) y, de allí,\(x = t\). Por lo tanto,\(f\) es una inyección.
Para probar que eso\(f\) es una sobrejección, vamos\(y \in (0, b)\). Ya que\(0 < y < b\), concluimos que\(0 < \dfrac{y}{b} < 1\) y que
\[f(\dfrac{y}{b}) - b(\dfrac{y}{b}\) = y.\]
Por lo tanto,\(f\) es una sobreyección y por lo tanto\(f\) es una biyección. Así,\((0, 1) \thickapprox (0, b)\).
Sección 9.2
Comprobación de Progreso 9.11
- El conjunto de números naturales\(\mathbb{N}\) es un subconjunto de\(\mathbb{Z}\),\(\mathbb{Q}\), y\(\mathbb{R}\). Dado que\(\mathbb{N}\) es un conjunto infinito, podemos usar la Parte (2) del Teorema 9.10 para concluir que\(\mathbb{Z}\),\(\mathbb{Q}\), y\(\mathbb{R}\) son conjuntos infinitos.
- Utilice la Parte (1) del Teorema 9.10.
- Demostrarlo\(\mathbb{E}^{+} \thickapprox \mathbb{N}\) y utilizar la Parte (1) del Teorema 9.10.
Comprobación de Progreso 9.12
- Usa la definición de un conjunto infinitamente contable.
- Ya que\(\mathbb{E}^{+} \thickapprox \mathbb{N}\), podemos concluir esa tarjeta\((E^{+}) = \aleph_{0}\).
- Una función que se puede utilizar está\(f: S \to \mathbb{N}\) definida por\(f(m) = \sqrt{m}\) para todos\(m \in S\).
Comprobación de Progreso 9.23
El Jugador Dos tiene una estrategia ganadora. En el turno\(k\) th, cualquiera que sea el símbolo que el Jugador Uno ponga en la posición\(k\)\(k\) th de la fila th, el Jugador Dos debe poner el otro símbolo en la posición\(k\) th de su fila. Esto garantiza que la fila de símbolos producida por el Jugador Dos será diferente a cualquiera de las filas producidas por el Jugador Uno.
Esta es la misma idea utilizada en el Argumento Diagonal de Cantor. Una vez que tenemos una “lista” de números reales en forma normalizada, creamos un número real que no está en la lista asegurándonos de que su\(k\) ésimo lugar decimal sea diferente a la\(k\) ésima posición decimal para el número\(k\) th en la lista. La única complicación es que debemos asegurarnos de que nuestro nuevo número real no tenga una expresión decimal que termine en todos los 9's, esto se hizo usando solo 3's y 5's.
Comprobación de Progreso 9.25
- Prueba. Para encontrar una bijección\(f: (0, 1) \to (a, b)\), utilizaremos la función lineal a través de los puntos\((0, a)\) y\((1, b)\). La pendiente es\((b - a)\) y la\(y\) -intercepción es\((0, a)\). Así definir\(f: (0, 1) \to (a, b)\) por
\[f(x) = (b - a) x + a, \text{for each } x \in (0, 1).\]
Ahora, si\(x, t \in (0, 1)\) y\(f(x) = f(t)\), entonces
\[(b - a)x + a = (b - a)t + a.\]
Esto implica que\((b - a) x = (b - a) t\), y desde\(b - a \ne 0\), e puede concluir que\(x = t\). Por lo tanto,\(f\) es una inyección.
Para probar que eso\(f\) es una sobrejección, dejamos\(y \in (a, b)\). Si\(x = \dfrac{y - a}{b - a}\), entonces
\[\begin{array} {rcl} {f(x)} &= & {f(\dfrac{y - a}{b - a})} \\ {} &= & {(b - a) (\dfrac{y - a}{b - a}) + a} \\ {} &= & {(y - a) + a} \\ {} &= & {y} \begin{array}\]
Esto demuestra que\(f\) es una sobrejección. De ahí,\(f\) es una biyección y\((0, 1) \thickapprox (a, b)\). Por lo tanto,\((a, b)\) es incontable y tiene cardinalidad\(c\). - Ahora bien, si\(a, b, c, d\) son números reales con\(a < b\) y\(c < d\), entonces sabemos que
\[(a, b) \thickapprox (0, 1) \text{ and } (c, d) \thickapprox (0, 1).\]
Since\(\thickapprox\) es una relación de equivalencia, podemos concluir que\((a, b) \thickapprox (c, d)\).


