Apéndice C: Respuestas y sugerencias para ejercicios seleccionados

Sección 1.1

1. Las oraciones (a), (c), (e), (f), (j) y (k) son declaraciones. Sentencia (h) es una declaración si estamos asumiendo que\(n\) es un número primo significa que\(n\) es un entero.

2. 	Hipótesis	Conclusión
   a.	\(n\)es un número primo.	\(n^2\)tiene tres divisores positivos.
   b.	\(a\)es un número irracional y\(b\) es un número irracional.	\(a \cdot b\)es un número irracional.
   c.	\(p\)es un número primo.	\(p = 2\)o\(p\) es un número impar.
   d.	\(p\)es un número primo y\(p \ne 2\).	\(p\)es un número impar.

3. Las declaraciones a), c) y d) son verdaderas.
4. (a) Cierto cuando\(a \ne 3\). (b) Cierto cuando\(a = 3\).

6. (a) Esta función tiene un valor máximo cuando\(x = \dfrac{5}{16}\).
c) No se puede llegar a ninguna conclusión sobre esta función.

9. a) El conjunto de números racionales no se cierra bajo división.
b) El conjunto de números racionales es no cerrado undre división ya que no se define la división por cero.
c) El conjunto de números racionales distintos de cero se cierra bajo división.
d) El conjunto de números racionales positivos se cierra bajo división.
e) El conjunto de números reales positivos no se cierra bajo resta.
f) El conjunto de números racionales negativos no se cierra bajo división.
(g) El conjunto de enteros negativos se cierra bajo suma.

Sección 1.2

1. (a)

   Paso	Conoce	Razón
   \(P\)	\(m\)es un número entero par.	Hipótesis
   \(P\)1	Existe un entero\(k\) tal que\(m = 2k\).	Definición de un entero par
   \(P\)2	\(m + 1 = 2k + 1\)	Álgebra
   \(Q\)1	Existe un entero\(q\) tal que\(m + 1 = 2q + 1\).	Sustitución de\(k = q\)
   \(Q\)	\(m + 1\)es un número entero impar.	Definición de un entero impar

2. (c) Suponemos que\(x\) y\(y\) son enteros impares y demostraremos que\(x + y\) es un entero par. Ya que\(x\) y\(y\) son impares, existen enteros\(m\) y\(n\) tal que\(x = 2m + 1\) y\(y = 2n + 1\). Entonces
   \[\begin{array} {rcl} {x + y} &= & {(2m + 1) + (2n + 1)} \\ {} &= & {2m + 2n + 2} \\ {} &= & {2(m + n + 1).} \end{array}\]
   Dado que los enteros se cierran bajo suma,\((m + n + 1)\) es un entero, y de ahí la última ecuación muestra que\(x + y\) es par. Por lo tanto, hemos demostrado que si\(x\) y\(y\) son enteros impares, entonces\(x + y\) es un entero par.
3. (b) Utilizar la Parte (a) para probar esto.

6. a) Demostrar que su diferencia es igual a cero o probar que no son cero y que su cociente es igual a 1.
d) Proveer que dos de los lados tienen el mismo sentido. Proveer que el triángulo tiene dos ángulos congruentes. Demostrar que una altitud del triángulo es una bisectriz perpendicular de un lado del triángulo.

9. (a) Algunos ejemplos de enteros de tipo 1 son -5, -2, 1, 4, 7, 10.
(c) Todo ejemplo debe indicar que la proposición es verdadera.

10. (a) Que a y b sean enteros y supongamos que a y b son ambos enteros de tipo 1. Entonces, existen enteros\(m\) y\(n\) tal que\(a = 3m + 1\) y\(b = 3n + 1\). Ahora demuestre que

\(a + b = 3 (m + n) + 2.\)

Las propiedades de cierre de los enteros implican que\(m + n\) es un entero. Por lo tanto, la última ecuación nos dice que\(a + b\) es un entero tipo 2. De ahí que hayamos demostrado que si\(a\) y\(b\) son ambos enteros tipo 1, entonces\(a + b\) es un entero tipo 2.

Sección 2.1

1. El enunciado era cierto. Cuando la hipótesis es falsa, la declaración condicional es verdadera.

2. (a)\(P\) es falso.
b)\(P \wedge Q\) es falso.
(c)\(P \vee Q\) es falso.

4. (c) No se puede decir si\(P \wedge R\) es verdadero o falso.

5. Las declaraciones (a) y (d) tienen la misma tabla de verdad. Las declaraciones (b) y (c) tienen las mismas tablas de verdad.

7. Las dos afirmaciones tienen la misma tabla de verdad.

9. (c) El entero\(x\) es par sólo si\(x^2\) es par.
(d) El entero\(x^2\) es par es necesario\(x\) para ser par.

Sección 2.2

1. (a) Converse: Si\(a^2 = 25\), entonces\(a = 5\). Contrapositivo: Si\(a^2 \ne 25\), entonces\(a \ne 5\).
(b) Converse: Si Laura está jugando al golf, entonces no está lloviendo. Contrapositivo: Si Laura no está jugando al golf, entonces está lloviendo.

2. a) Disyunción:\(a \ne 5\) o\(a^2 = 25\). Negación:\(a = 5\) y\(a^2 = 25\).
b) Disyunción: Está lloviendo o Laura está jugando al golf. Negación: No está lloviendo y Laura no está jugando al golf.

3. (a) No ganaremos el primer juego o no ganaremos el segundo juego.
(c) Siegas el césped y no te voy a pagar 20 dólares.
(f) Egresas de la universidad, y no conseguirás empleo y no irás a la escuela de posgrado.

7. a) En este caso, puede ser mejor trabajar primero con el lado derecho.

\(\begin{array} {rcl} {(P \to R) \vee (Q \to R)} &\equiv & {(\urcorner R \vee R) \vee (\urcorner Q \vee R)} \\ {} &\equiv & {(\urcorner R \vee \urcorner Q) \vee (R \vee R)} \\ {} &\equiv & {(\urcorner R \vee \urcorner Q) \vee R} {} &\equiv & {\urcorner (P \vee Q) \vee R} \\ {} &\equiv & {(P \wedge Q) \to R.} \end{array}\)

10. Las declaraciones (c) y (d) son lógicamente equivalentes a la declaración condicional dada. Declaración (f) es la negación de la declaración condicional dada.
11. d) Este es el contrapositivo del enunciado dado y por lo tanto, es lógicamente equivalente al enunciado dado.

Sección 2.3

1. (a)\(\dfrac{1}{2}, -2\}\)
(d)\(\{1, 2, 3, 4\}\) |
(e)\(\{0.5, 4.5\}\)

2. \(A = \{n ^2\ |\ n \in \mathbb{N}\)
\(D = \{4n\ |\ n \text{is a nonnegative integer and } 0 \le n \le 25\}\)

3. Los conjuntos en (b) y (c) son iguales al conjunto dado.

5. a\(\{x \in \mathbb{Z}\ |\ x \le 5\}\)
) e\(\{x \in \mathbb{R]\ |\ x^2 > 10\}\)

Sección 2.4

1. (a) Existe un número racional x tal que\(x^2 - 3x - 7 = 0\). Esta afirmación es falsa ya que las soluciones de la ecuación son\(x = \dfrac{3 \pm \sqrt{37}}{2}\), que son números irracionales.

2. b)\(x = 0\) es un contraejemplo. La negación es: Existe un número real\(x\) tal que\(x^2 \le 0\).
(g)\(x = \dfrac{\pi}{2}\) es un contraejemplo. La negación es: Existe un número real\(x\) tal que\(\text{tan}^2x + 1 \ne \text{sec}^2 x\).

3. a) Existe un número racional\(x\) tal que\(x > \sqrt{2}\).
La negación es\((\forall x \in \mathbb{Q})(x \le \sqrt{2})\), que es, Por cada número racional\(x\),\(x \le \sqrt{2}\).

(c) Por cada entero\(x\),\(x\) es par o\(x\) es impar.
La negación es\((\exists x \in \mathbb{Z}\) (\(x\)es impar y\(x\) es par), que es, Existe un entero\(x\) tal que\(x\) es impar y\(x\) es par.

(e) Por cada entero\(x\), si\(x^2\) es impar, entonces\(x\) es impar.
La negación es\((\exists x \in \mathbb{Z}\) (\(x^2\)es impar y\(x\) es par), que es, Existe un entero\(x\) tal que\(x^2\) es impar y\(x\) es par.
(h) Existe un número real\(x\) tal que cos (2\(x\)) = 2 (cos\(x\)).
La negación es\((\forall x \in \mathbb{R}\) (cos (2\(x\))\(\ne\) 2 (cos\(x\))), que es, Por cada número real\(x\), cos (2\(x\))\(\ne\) 2 (cos\(x\)).

4. (a) Existen enteros\(m\) y\(n\) tal que\(m > n\).
(c) Existe un entero\(n\) tal que para cada ineger\(m\),\(m^2 > n\).

5. a)\((\forall m)(\forall n)(m \le n)\).
Para todos los inetgers\(m\) y\(n\),\(m \le n\).
e)\((\forall n)(\exists m)(m^2 \le n)\).
Para cada entero\(n\), existe un entero\(m\) tal que\(m^2 \le n\).

10. (a) Una función\(f\) con dominio\(\mathbb{R}\) es estrictamente creciente siempre que\((\forall x, y \in \mathbb{R})[(x < y) \to (f(x) < f(y))]\).

Sección 3.1

1. (a) Recuerda que para probarlo\(a\ |\ (b - c)\), necesitas probar que existe un entero\(q\) tal que\(b - c = a \cdot q\).
b) ¿Qué hay que hacer para demostrar que\(n^3\) es extraño? Observe que ifn es un entero impar, entonces existe un entero\(k\) tal que\(n = 2k + 1\). Recuerda que para probar que\(n^3\) es un entero impar, necesitas probar que existe un entero\(q\) tal que\(n^3 = 2q + 1\).
O puedes acercarte a esto de la siguiente manera: Si\(n\) es impar, entonces por el Teorema 1.8,\(n^2\) es impar. Ahora usa el hecho de que\(n^3 = n \cdot n^2\).
(c) Si 4 divide\((a - 1)\), entonces existe un entero\(k\) tal que\(a - 1 = 4k\). Escribe\(a = 4k + 1\) y luego usa álgebra para reescribir\((a^2 - 1)\).

3. (e) Asegúrese de probar primero algunos ejemplos. ¿Cómo se prueba que un entero es un número entero impar?
f) El siguiente álgebra puede ser útil.

\(4(2m + 1)^2 + 7(2m + 1) + 6 = 6m^2 + 30m + 17.\)

4. (a) Si\(xy = 1\), entonces\(x\) y\(y\) son ambos divisores de 1, y los únicos divisores de 1 son -1 y 1.|
(b) La parte (a) es útil para probar esto.

3. Vamos\(n \in \mathbb{N}\). Para\(a, b \in \mathbb{Z}\), es necesario demostrar que si\(a \equiv b\) (mod\(n\)), entonces\(b \equiv a\) (mod\(n\)). Recuerda eso para\(x, y \in \mathbb{Z}\),\(x \equiv y\) (mod\(n\)) si y solo si\(n\ |\ (x - y)\).

5. Otra pista:\((4n + 3) - 2(2n + 1) = 1\).

8. (a) Suponiendo\(a\) y ambos\(b\) son congruentes a 2 módulo 3, existen enteros\(m\) y\(n\) tales que\(a = 3m + 2\) y\(b = 3n + 2\). Entonces demuéstrale

\(a + b = 3(m + n + 1) + 1\)

12. Los supuestos significan eso\(n\ |\ (a - b)\) y eso\(n\ |\ (c - d)\). Utilice estas relaciones de divisibilidad para obtener una expresión que sea igual a a y para obtener una expresión que sea igual a c. Luego use álgebra para reescribir las expresiones resultantes para\(a + c\) y\(a \cdot c\).

Sección 3.2

1. (a) Dejar\(n\) ser un entero par. Ya que\(n\) es par, existe un entero\(k\) tal que\(n = 2k\). Ahora usa esto para demostrar que\(n^3\) debe ser parejo.
b) Demostrar el contrapositivo.
c) Explique por qué las Partes (a) y (b) lo prueban.
d) Explique por qué las Partes (a) y (b) lo prueban.

2. (a) El contrapositivo es, Para todos los enteros\(a\) y\(b\), si\(ab \equiv 0\) (mod 6), entonces\(a \equiv 0\) (mod 6) o\(b \equiv 0\) (mod 6).

4. (a) Si\(a \equiv 2\) (mod 5), entonces existe un entero\(k\) tal que\(a - 2 = 5k\). Entonces\(a^2 = (2 + 5k)^2 = 4 + 20k + 25k^2\). Esto significa que\(a^2 - 4 = 5(4k + 5k^2)\).

6. Una de las dos declaraciones condicionales es verdadera y otra es falsa.

8. Demostrar ambas declaraciones condicionales: (1) Si el área del triángulo rectángulo es\(c^2/4\), entonces el triángulo rectángulo es un triángulo isósceles. (2) Si el triángulo rectángulo es un triángulo isósceles, entonces el área del triángulo rectángulo es\(c^2/4\).

9. Demostrar el contrapositivo.

10. Recuerde que hay dos declaraciones condicionales asociadas a esta declaración bicondicional. Estar dispuesto a considerar el contrapositivo de una de estas declaraciones condicionales.

15. Definir una función apropiada y utilizar el Teorema del Valor Intermedio.

17. (b) Puesto que 4 divide\(a\), existe un entero\(n\) tal que\(a = 4n\). Usando esto, vemos eso\(b^3 = 16n^2\). Esto quiere decir que b3 es par y por lo tanto por Ejercicio (1),\(b\) es par. Entonces existe un entero\(m\) tal que\(b = 2m\). Usa esto para demostrar que\(m^3\) debe ser parejo y por lo tanto por el Ejercicio (1),\(m\) es parejo.

18. Puede ser necesario factorial una suma de cubos. Recordemos que

\(u^3 + v^3 = (u + v)(u^2 - uv + v^2).\)

Sección 3.3

1. a)\(P \vee C\)

3. (a) Que\(r\) sea un número real tal que\(r^2 = 18\). Demostraremos que\(r\) es irracional usando una prueba por contradicción. Entonces asumimos que\(r\) es un número racional.
(b) No intentar imitar la prueba de que la raíz cuadrada de 2 es irracional (Teorema 3.20). Aún debes usar la definición de un número racional pero luego usar el hecho de que\(\sqrt{18} = \sqrt{9 \cdot 2} = \sqrt{9} \sqrt{2} = 3\sqrt{2}\).

5. En cada parte, ¿cuál es el contrapositivo de la proposición? ¿Por qué parece que lo contrapositivo no será un buen enfoque? Por cada enunciado, intente una prueba por contradicción.

6. Dos de las proposiciones son verdaderas y las otras dos falsas.

11. Recordemos que ese\(\text{log}_2 32\) es el número real\(a\) tal que\(2^{a} = 32\). Es decir,\(a = \text{log}_2 32\) significa eso\(2^{a} = 32\). Si asumimos que eso\(a\) es racional, entonces existen enteros\(m\) y\(n\), con\(n \ne 0\), tal que\(a = \dfrac{m}{n}\).

12. Pista: Los únicos factores de 7 son -1, 1, -7 y 7.

13. (a) ¿Qué pasa si expandes (sin\(\theta\) + cos\(\theta\))\(^2\)? No olvides las identidades trigonométricas.

14. Sugerencia: Tres números naturales consecutivos pueden ser representados por\(n\)\(n + 1\),, y\(n + 2\), donde\(n \in \mathbb{N}\), o tres números naturales consecutivos pueden ser representados por\(m - 1\),\(m\) y\(m + 1\), dónde\(m \in \mathbb{N}\).

Sección 3.4

1. Usa el hecho de que\(n^2 + n = n(n + 1)\).

2. No utilice la fórmula cuadrática. Prueba una prueba por contradicción. Pista: Si existe una solución de la ecuación que es un entero, entonces podemos concluir que existe un entero\(n\) tal que\(n^2 + n - u = 0\).

3. Primero escribe\(n = 2m + 1\) para algún número entero\(m\). El entero\(m\) puede ser par o impar.

5. (c) Para todos los enteros\(a\)\(b\),, y\(d\) con\(d \ne 0\), si\(d\) divide el producto\(ab\), entonces\(d\) divide\(a\) o\(d\) divdes\(b\).

8. Prueba una prueba por contradicción con dos casos:\(a\) es par o\(a\) es impar.

10. a) Una forma es utilizar tres casos: i)\(x > 0\); ii)\(x = 0\); y\(x < 0\). Para el primer caso,\(-x < 0\) y\(|-x| = -(-x) = x = |x|\).

11. a) Por cada número real\(x\),\(|x| \ge a\) si y sólo si\(x \ge a\) o\(x \le -a\).

Sección 3.5

2. b) Factor\(n^3 - n\).
c) Considerar el uso de casos basados en congruencia módulo 6.

3. Vamos\(n \in \mathbb{N}\). Para\(a, b \in \mathbb{Z}\), es necesario demostrar que si\(a \equiv b\) (mod\(n\)), entonces\(b \equiv a\) (mod\(n\)). Recuerda eso para\(a, b \in \mathbb{Z}\), si\(a \equiv b\) (mod\(n\)), entonces\(n\ |\ (a - b)\). Entonces existe un entero\(k\) tal que\(a - b = nk\).

4. a) Utilizar la definición de congruencia.
b) Dejar\(a \in \mathbb{Z}\). Corolario 3.32 nos dicen que si\(a \not\equiv 0\) (mod 3), entonces\(a \equiv 1\) (mod 3) o\(a \equiv 2\) (mod 3).
(c) Para una de las declaraciones condicionales, la Parte (b) nos dice que podemos usar una prueba por casos usando los siguientes dos casos: (1)\(a \equiv 1\) (mod 3); (2)\(a \equiv 2\) (mod 3).

6. El resultado en la Parte (c) del Ejercicio (4) puede ser útil en una prueba por contradicción.

8. (a) Recuerda que\(3\ |\ k\) si y solo si\(k \equiv 0\) (mod 3).

9. a) Utilizar una prueba similar a la prueba del Teorema 3.20. El resultado del Ejercicio (8) puede ser útil.

12. (a) Utilizar los resultados del Teorema 3.28 para demostrar que el resto debe ser 1.

Sección 4.1

1. Los conjuntos de las Partes (a) y (b) son inductivos.

2. Un conjunto finito no vacío no es inductivo (¿por qué?) pero el conjunto vacío es inductivo (¿por qué?).

3. (a) Para cada uno\(n \in \mathbb{N}\),\(P(n)\) déjese,\(2 + 5 + 8 + \cdot\cdot\cdot + (3n - 1) = \dfrac{n(3n + 1)}{2}.\) Verificar que\(P(1)\) sea cierto. La clave del paso inductivo es que si\(P(k)\) es cierto, entonces

\(\begin{array} {rcl} {2 + 5 + 8 + \cdot\cdot\cdot + (3k - 1) + [3(k + 1) - 1]} &= & {(2 + 5 + 8 + \cdot\cdot\cdot + (3k - 1)) + (3k + 2)} \\ {} &= & {\dfrac{3k(k + 1)}{2} + (3k + 2).} \end{array}\)

Ahora usa álgebra para mostrar que la última expresión se puede reescribir como\(\dfrac{(k + 1)(3k + 4)}{2}\) y luego explicar por qué esto completa la prueba de que si\(P(k)\) es verdadera, entonces\(P(k + 1)\) es verdadera.

6. La conjetura es que para cada uno\(n \in \mathbb{N}\),\(\sum_{j = 1}^{n} (2j - 1) = n^2\). La clave del paso inductivo es que

\(\begin{array} {rcl} {\sum_{j = 1}^{k + 1} (2j - 1)} &= & {\sum_{j = 1}^{k} (2j - 1) + [2(k + 1) - 1]} \\ {} &= & {\sum_{j = 1}^{k} (2j - 1) + [2k + 1].} \end{array}\)

8. a) La clave del paso inductivo es que si\(4^k = 1 + 3m\), entonces\(4^{k} \cdot 4 = 4(1 + 3m)\), lo que implica que

\(4^{k + 1} - 1 = 3(1 + 4m).\)

13. Dejar\(k\) ser un número natural. Si\(a^k \equiv b^k\) (mod\(n\)), entonces ya que también estamos asumiendo que\(a \equiv b\) (mod\(n\)), podemos usar la Parte (2) del Teorema 3 para concluir que\(a \cdot a^k \equiv b \cdot b^k\) (mod\(n\)).

14. Tres números naturales consecutivos pueden representar por\(n\),\(n + 1\), y\(n + 2\), donde\(n\) es un número natural. Para el paso inductivo, piensa antes de intentar hacer mucho álgebra. Deberías poder completar una prueba del paso inductivo expandiendo el cubo de una sola expresión.

Sección 4.2

1. (a) Si\(P(k)\) es cierto, entonces\(3^k > 1 + 2^k\). Multiplicando ambos lados de esta desigualdad por 3 da

\(3^{k + 1} > 3 + 3 \cdot 2^k\)

Ahora, desde\(3 > 1\) y\(3 \cdot 2^k > 2^{k + 1}\), vemos eso\(3 + 3 \cdot 2^k > 1 + 2^{k + 1}\) y por lo tanto,\(3^{k + 1} > 1 + 2^{k + 1}\). Así, si\(P(k)\) es ture, entonces\(P(k + 1)\) es verdad.

2. Si\(n \ge 5\), entonces\(n^2 < 2^n\). Para el paso inductivo, asumimos eso\(k^2 < 2^k\) y aquello\(k \ge 5\). Con estos supuestos, demostrar que

\((k + 1)^2 = k^2 + 2k + 1 < 2^{k} + 2k + 1.\)

Ahora usa la suposición que\(k > 4\) para probar eso\(2k + 1 < k^2\) y combinar esto con el supuesto de que\(k^2 < 2^k\).

5. \(P(n)\)Sea el predicado, "\(8^n\ |\ (4n)!\).” Verificar que\(P(0)\),\(P(1)\),\(P(2)\), y\(P(3)\) son ciertas. Para el paso inductivo, el siguiente dato sobre factoriales puede ser útil:

\(\begin{array} {rcl} {[4(k + 1)]!} &= & {(4k + 4)!} \\ {} &= & {(4k + 4)(4k + 3)(4k + 2)(4k + 1)(4k)!.} \end{array}\)

8. \(P(n)\)Sea, “El número natural\(n\) puede escribirse como una suma de números naturales, cada uno de los cuales es un 2 o un 3”. Verificar que\(P(4)\),\(P(5)\),\(P(6)\), y\(P(7)\) son ciertas.

Para utilizar el Segundo Principio de Inducción Matemática, supongamos que\(k \in \mathbb{N}\),\(k \ge 5\) y que\(P(4)\),\(P(5)\),... \(P(k)\)son ciertas. Entonces note que

\(k + 1 = (k - 1) + 2.\)

Ya que\(k - 1 \le 4\), hemos supuesto que eso\(P(k - 1)\) es cierto. Use esto para completar el paso inductivo.

12. Let\(P(n)\) be, “Cualquier conjunto con\(n\) elementos tiene subconjuntos de\(\dfrac{n(n - 1)}{2}\) 2 elementos”. \(P(1)\)es true ya que cualquier conjunto con un solo elemento no tiene subconjuntos de 2 elementos. Dejemos\(k \in \mathbb{N}\) y supongamos que eso\(P(k)\) es cierto. Esto significa que cualquier conjunto con\(k\) elementos tiene subconjuntos de\(\dfrac{k(k - 1)}{2}\) 2 elementos. Dejar\(A\) ser un conjunto con\(k + 1\) elementos, y dejar\(x \in A\). Ahora use la hipótesis inductiva en el conjunto\(A - \{x\}\) y determine cómo los subconjuntos de 2 elementos de\(A\) están relacionados con el conjunto\(A - \{x\}\).

16. a) Usar Teorema 4.9
b) Asumir\(k \ne q\) y considerar dos casos: (i)\(k < q\); (ii)\(k > q\).

Sección 4.3

1. Para el paso inductivo, si\(a_k = k!\), entonces

\(\begin{array} {rcl} {a_{k + 1}} &= & {(k + 1)a_{k}} \\ {} &= & {(k + 1)k!} \\ {} &= & {(k + 1)!.} \end{array}\)

2. (a) Let\(P(n)\) be, "\(f_{4n}\)es un múltiplo de 3.” Ya que\(f_4 = 3\),\(P(1)\) es cierto. Si\(P(k)\) es cierto, entonces existe un entero\(m\) tal que\(f_{4k} = 3m\). Utilice lo siguiente:

\(\begin{array} {rcl} {f_{4(k + 1)}} &= & {f_{4k + 4}} \\ {} &= & {f_{4k + 3} + f_{4k + 2}} \\ {} &= & {(f_{4k + 2} + f_{4k + 1}) + (f_{4k + 1} + f_{4k})} \\ {} &= & {f_{4k + 2} + 2f_{4k + 1} + f_{4k}} \\ {} &= & {(f_{4k + 1} + f_{4k}) + 2f_{4k + 1} + f_{4k}.} \end{array}\)

c)\(P(n)\) Sea, "\(f_1 + f_2 + \cdot\cdot\cdot + f_{n - 1} = f_{n + 1} - 1\).” Ya que\(f_1 = f_3 - 1\),\(P(2)\) es cierto. Porque\(k \ge 2\), si\(k \ge 2\), si\(P(k)\) es verdad, entonces\(f_1 + f_2 + \cdot\cdot\cdot + f_{k - 1} = f_{k + 1} - 1\). Entonces

\(\begin{array} {rcl} {f_1 + f_2 + \cdot\cdot\cdot + f_{k - 1}) + f_{k}} &= & {(f_{k + 1} - 1) + f_{k}} \\ {} &= & {(f_{k + 1} + f_{k}) - 1} \\ {} &= & {f_{k + 2} - 1.} \end{array}\)

Esto prueba que si\(P(k)\) es verdad, entonces\(P(k + 1)\) es verdad.

f)\(P(n)\) Sea, "\(f_{1}^{2} + f_{2}^{2} + \cdot\cdot\cdot + f_{n}^{2} = f_{n}f_{n + 1}\).” Para el paso inductivo, use

\(\begin{array} {rcl} {(f_{1}^{2} + f_{2}^{2} + \cdot\cdot\cdot + f_{k}^{2}) + f_{k + 1}^2} &= & {f_{k}f_{k + 1} + f_{k + 1}^{2}} \\ {f_{1}^{2} + f_{2}^{2} + \cdot\cdot\cdot + f_{k}^{2} + f_{k + 1}^2} &= & {f_{k + 1}(f_{k} + f_{k + 1})} \\ {} &= & {f_{k + 1}f_{k + 2}.} \end{array}\)

6. Para el paso inductivo, si\(a_k = a \cdot r^{k - 1}\), entonces

\(\begin{array}{rcl} {a_{k + 1}} &= & {r \cdot a_{k}} \\ {} &= & {r(a \cdot r^{k - 1})} \\ {} &= & {a \cdot r^{k}.} \end{array}\)

8. Para el paso inductivo, use la suposición que\(S_{k} = a(\dfrac{1 - r^{k}{1 - r})\) y la definición recursiva para escribir\(S_{k + 1} = a + r \cdot S_{k}\).

9. (a)\(a_2 = 7\),\(a_3 = 12\),\(a_4 = 17\),\(a_5 = 22\),\(a_6 = 27\).
b) Una posibilidad es: Para cada uno\(n \in \mathbb{N}\),\(a_n = 2 + 5(n - 1)\).

12. a)\(a_2 = \sqrt{6}\),\(a_3 = \sqrt{\sqrt{6} + 5} \thickapprox 2.729\),\(a_4 \thickapprox 2.780\),\(a_5 \thickapprox 2.789\),\(a_6 \thickapprox 2.791\)
b)\(P(n)\) Sea, "\(a_n < 3\).” Ya que\(a_1 = 1\),\(P(1)\) es cierto. Porque\(k \in \mathbb{N}\), si\(P(k)\) es verdad, entonces\(a_{k} < 3\). Ahora

\(a_{k + 1} = \sqrt{5 + a_k}.\)

Ya que\(a_{k} < 3\), esto implica eso\(a_{k + 1} < \sqrt{8}\) y por lo tanto,\(a_{k + 1} < 3\). Esto prueba que si\(P(k)\) es verdad, entonces\(P(k + 1)\) es verdad.

13. (a)\(a_3 = 7\),\(a_4 = 15\),\(a_5 =31\),\(a_6 = 63\)
(b) Pensar en términos de poderes de 2.

14. (a)\(a_3 = \dfrac{3}{2}\)\(a_4 = \dfrac{7}{4}\),\(a_5 = \dfrac{37}{24}\),\(a_6 = \dfrac{451}{336}\)

16. b)\(a_2 = 5\)\(a_2 = 719\)\(a_8 = 362879\)
\(a_3 = 23\)\(a_2 = 5039\)\(a_9 = 3628799\)
\(a_4 = 119\)\(a_2 = 40319\) \(a_{10} = 39916799\)

18. a)\(P(n)\) Sea, "\(L_{n} = 2f_{n + 1} - f_{n}\).” Primero,\(P(1)\) verifíquelo y\(P(2)\) sean ciertos. Ahora vamos a\(k\) ser un número natural con\(k \ge 2\) y asumir que\(P(1)\),\(P(2)\),...,\(P(k)\) son todos ciertos. Como\(P(k)\) y\(P(k - 1)\) se supone que ambos son ciertos, podemos utilizarlos para ayudar a demostrar que entonces\(P(k + 1)\) debe ser cierto de la siguiente manera:

\(\begin{array} {rcl} {L_{k + 1}} &= & {L_{k} + L_{k - 1}} \\ {} &= & {(2f_{k + 1} - f_{k}) + (2f_{k} - f_{k - 1})} \\ {} &= & {2(f_{k + 1} + f_{k}) - (f_{k} + f_{k - 1}} \\ {} &= & {2f_{k + 2} - f_{k + 1}.} \end{array}\)

b)\(P(n)\) Sea, "\(5f_{n} = L_{n - 1} + L_{n + 1}\).” Primero,\(P(2)\) verifíquelo y\(P(3)\) sean ciertos. Ahora vamos a\(k\) ser un número natural con\(k \ge 3\) y asumir que\(P(2)\),\(P(3)\),...,\(P(k)\) son todos ciertos. Como\(P(k)\) y\(P(k - 1)\) se supone que ambos son ciertos, podemos utilizarlos para ayudar a demostrar que entonces\(P(k + 1)\) debe ser cierto de la siguiente manera:

\(\begin{array} {rcl} {5f_{k + 1}} &= & {5f_{k} + 5_{k - 1}} \\ {} &= & {(L_{k - 1} + L_{k + 1}) + (L_{k - 2} + L{k})} \\ {} &= & {(L_{k - 1} + L_{k - 2}) - (L_{k} + L_{k + 1})} \\ {} &= & {L_{k} + L_{k + 2}.} \end{array}\).

Sección 5.1

1. a\(A = B\)) c\(C \ne D\)) e\(A \not\subseteq D\)
) b\(A \subseteq B\)) d\(C \subseteq D\)

2. En ambos casos, los dos conjuntos tienen precedentemente los mismos elementos.

3.
\(\begin{array} {rclrcl} {A} &\subset, \subseteq, \ne & {B} {\emptyset} &\subset, \subseteq, \ne & {A} \\ {5} &\in & {C} {\{5\}} &\subset, \subseteq, \ne & {C} \\ {|A|} &= & {|D|} {A} &\in & {\mathcal{P}(b)} \end{array}\)
5. (a) El conjunto no\(\{a, b\}\) es un subconjunto de\(\{a, c, d, e\}\) since\(b \in \{a, b\}\) y\(b \in \{a, c, d, e\}\).

7. (c)\((A \cup B)^{c} = \{2, 8, 10\}\) (h)\((A \cap C) \cup (B \cap C) = \{3, 6, 9\}\)
(d)\(A^{c} \cap B^{c} = \{2, 8, 10\}\) (n)\((A \cup B) - D = \{1, 3, 5, 7, 9\}\)
(e)\((A \cup B) \cap C = \{3, 6, 9\}\)

9. b) Existe\(x \in U\) tal que\(x \in (P - Q)\) y\(x \notin (R \cap S)\). Esto se puede escribir como, Existe\(x \in U\) tal que\(x \in P\),\(x \notin Q\), y\(x \notin R\) o\(x \notin S\).

10. a) El enunciado dado es un enunciado condicional. Podemos reescribir las relaciones de subconjunto en términos de oraciones condicionales:\(A \subseteq B\) significa, “Para todos\(x \in U\)\(x \in A\), si\(x \in B\), entonces” y\(B^{c} \subseteq A^{c}\) significa, “Para todos\(x \in U\), si\(x \in B^{c}\), entonces”\(x \in A^{c}\).

Sección 5.2

1. (a) El conjunto\(A\) es un subconjunto de\(B\). Se requiere una prueba. La idea es que si\(x \in A\), entonces\(-2 < x < 2\). Ya que\(x < 2\), concluimos que\(x \in B\).
(b) El conjunto no\(B\) es un subconjunto de\(A\). Dar un ejemplo de un número real que está en\(B\) pero no en\(A\).

3. b)\(A \subseteq B\)\(B \not\subseteq A\)

7. (a) Empezar por dejar\(x\) ser un elemento de\(A \cap B\).
(b) Empezar por dejar\(x\) ser un elemento de\(A\).
(e) Por teorema 5.1,\(\emptyset \subseteq A \cap \emptyset\). Por la Parte (a),\(A \cap \emptyset \subseteq \emptyset\). Por lo tanto,\(A \cap \emptyset = \emptyset\).

12. (a) Dejar\(x \in A \cap C\). Entonces\(x \in A\) y\(x \in C\). Ya que estamos asumiendo eso\(A \subseteq B\), vemos eso\(x \in B\) y\(x \in C\). Esto lo demuestra\(A \cap C \subseteq B \cap C\).

15. a) “Si\(A \subseteq B\), entonces\(A \cap B^{c} = \emptyset\)" es la Proposición 5.14. Para probar la otra declaración condicional, comience con, “Vamos”\(x \in A\). Entonces usa la suposición de que\(A \cap B^{c} = \emptyset\) para probar eso\(x\) debe estar en\(B\).
b) Para probar “Si\(A subseteq B\), entonces”\(A \cup B = B\), primero tenga en cuenta que si\(x \in B\), entonces\(x \in A \cup B\) y, por lo tanto,\(B \subseteq A \cup B\). Ahora vamos\(x \in A \cup B\) a señalar que desde\(A \subseteq B\), si\(x \in A\), entonces\(x \in B\). Utilice esto para argumentar que bajo el supuesto de que\(A \subseteq B\),\(A \cup B \subseteq B\).

Tp probar “Si\(A \cup B = B\), entonces\(A \subseteq B\),” empezar con, Let\(x \in A\) y utilizar esta asusmption para probar que\(x\) debe ser un elemento de\(B\).

Sección 5.3

1. (a) Dejar\(x \in (A^{c})^{c}\). Entonces\(x \notin A^{c}\), lo que significa\(x \in A\). De ahí,\((A^{c})^{c} \subseteq A\). Ahora demuéstralo\(A \subseteq (A^{c})^{c}\).
(c) Dejar\(x \in U\). Entonces\(x \notin \emptyset\) y así\(x \in \emptyset^{c}\). Por lo tanto,\(U \subseteq \emptyset^{c}\). Además, dado que cada conjunto que tratamos es un subconjunto del conjunto universal,\(\emptyset^{c} \subseteq U\).

2. Primero lo demostraremos\(A \cap (B \cup C) \subseteq (A \cap B) \cup (A \cap C)\). Vamos\(x \in A \cap (B \cup C)\). Entonces\(x \in A\) y\(x \in B \cup C\). Entonces usaremos dos casos: (1)\(x \in B\); (2)\(x \in C\). En el Caso (1),\(x \in A \cap B\) y, por lo tanto\(x \in (A \cap B) \cup (A \cap C)\). En el Caso (2),\(x \in A \cap C\) y, por lo tanto,\(x \in (A \cap B) \cup (A \cap C)\). Esto lo demuestra\(A \cap (B \cup C) \subseteq (A \cap B) \cup (A \cap C)\).

Ahora demuéstralo\((A \cap B) \cup (A \cap C) \subseteq A \cap (B \cup C)\).

4. a)\(A - (B \cup C) = (A - B) \cap (A - C)\).
(c) Utilizando el álgebra de conjuntos, obtenemos

\(\begin{array} {rcl} {(A - B) \cap (A - C)} &= & {(A \cap B^{c}) \cap (A \cap C^{c})} \\ {} &= & {(A \cap A) \cap (B^{c} \cap C^{c})} \\ {} &= & {A \cap (B \cup C)^{c}} \\ {} &= & {A - (B \cup C).} \end{array}\)

9. a) Utilizar una prueba por contradicción. Supongamos que los conjuntos no son disjuntos y vamos\(x \in A \cap (B - A)\). Entonces\(x \in A\) y\(x \in B - A\), lo que implica eso\(x \notin A\).

Sección 5.4

1, a)\(A \times B = \{(1, a), (1, b), (1, c), (1, d), (2, a), (2, b), (2, c), (2, d)\}\)
b)\(B \times A = \{(a, 1), (b, 1), (c, 1), (d, 1), (a, 2), (b, 2), (c, 2), (d, 2)\}\)
c)\(A \times (B \cap C) = \{(1, a), (1, b), (2, a), (2, b)\}\)

3. Inicio de prueba de que\(A \times (B \cap C) \subseteq (A \times B) \cap (A \times C)\):
Vamos\(u \in A \times (B \cap C)\). Entonces existe\(x \in A\) y existe\(y \in B \cap C\) tal que\(u = (x, y)\). Ya que\(y \in B \cap C\), sabemos que\(y \in B\) y\(y \in C\). Así que tenemos

\(u = (x, y)\), donde\(x \in A\) y\(y \in B\). Esto significa que\(u \in A \times B\).
\(u = (x, y)\), donde\(x \in A\) y\(y \in C\). Esto significa que\(u \in A \times C\).

4. Inicio de comprobante de que\((A \cup B) \times C \subseteq (A \times C) \cup (B \times C)\):

dejar\(u \in (A \cup B) \times C\). Entonces existe\(x \in A \cup B\) y existe\(y \in C\) tal que\(u = (x, y)\). Ya que\(x \in A \cup B\), sabemos que\(x \in A\) o\(x \in B\).

Sección 5.5

1. (a) {3, 4}
(d) {3, 4, 5, 6, 7, 8, 9, 10}

2. (a) {5, 6, 7,...}
c) d\(\emptyset\)
) {1, 2, 3, 4} f
)\(\emptyset\)

3. a\(\{x \in \mathbb{R}\ |\ -100 \le x \le 100\}\)
) b\(\{x \in \mathbb{R}\ |\ -1 \le x \le 1\}\)

4. (a) Dejamos\(\beta \in \Lambda\) y dejamos\(x \in A_{\beta}\). Entonces\(x \in A_{\alpha}\), para al menos uno\(\alpha \in \Lambda\) y, de ahí,\(x \in \bigcup_{\alpha \in \Lambda} A_{\alpha}\). Esto lo demuestra\(A_{\beta} \subseteq \bigcup_{\alpha \in \Lambda} A_{\alpha}\).

5. (a) Primero dejamos\(x \in B \cap (\bigcup_{\alpha \in \Lambda} A_{\alpha})\). Entonces\(x \in B\) y\(x \in \bigcup_{\alpha \in \Lambda} A_{\alpha}\). Esto quiere decir que existe\(\alpha \in \Lambda\) tal que\(x \in A_{\alpha}\). De ahí,\(x \in B \cap A_{\alpha}\), lo que implica que\(x \in \bigcup_{\alpha \in \Lambda} (B \cap A_{\alpha})\). Esto lo prueba\(B \cap (\bigcup_{\alpha \in \Lambda} A_{\alpha}) \subseteq \bigcup_{\alpha \in \Lambda} (B \cap A_{\alpha})\), y todavía tenemos que probarlo\(\bigcup_{\alpha \in \Lambda} (B \cap A_{\alpha}) \subseteq B \cap (\bigcup_{\alpha \in \Lambda} A_{\alpha})\).

8. (a) Dejar\(x \in B\). Para cada uno\(\alpha \in \Lambda\),\(B \subseteq A_{\alpha}\) y, de ahí,\(x \in A_{\alpha}\). Esto significa que para cada uno\(\alpha \in \Lambda\),\(x \in A_{\alpha}\) y, de ahí,\(x \in \bigcap_{\alpha \in \Lambda} A_{\alpha}\). Por lo tanto,\(B \subseteq \bigcap_{\alpha \in \Lambda} A_{\alpha}\)

12. (a) Primero reescribimos la diferencia establecida y luego usamos una ley distributiva.

\(\begin{array} {rcl} {(\bigcup_{\alpha \in \Lambda} A_{\alpha}) - B} &= & {(\bigcup_{\alpha \in \Lambda} A_{\alpha}) \cap B^{c}} \\ {} &= & {\bigcup_{\alpha \in \Lambda} (A_{\alpha} \cap B^{c})} \\ {} &= & {\bigcup_{\alpha \in \Lambda} (A_{\alpha} - B)} \end{array}\)

Sección 6.1

1. (a)\(f(-3) = 15\),\(f(-1) = 3\),\(f(1) = -1\),\(f(3) = 3\).
(b) El conjunto de preimágenes de 0 es {0, 2}. El conjunto de preimágenes de 4 es {\(\dfrac{2 - \sqrt{20}}{2}, \dfrac{2 + \sqrt{20}}{2}\)}. (Utilice la fórmula cuadrática.)
(d) rango\((f) = \{y \in \mathbb{R}\ |\ y \ge -1\}\).

4. (b) El conjunto de preimágenes de 5 es {2}. Hay conjunto de preimágenes de 4 es\(\emptyset\).
(c) El rango de la función\(f\) es el conjunto de todos los enteros impares.
d) La gráfica de la función\(f\) consiste en un conjunto infinito de puntos discretos.

5. (b) dom\((F) = \{x \in \mathbb{R}\ |\ x > \dfrac{1}{2}\}\), rango\((F) = \mathbb{R}\)
(d) dom\((g) = \{x \in \mathbb{R}\ |\ x \ne 2 \text{ and } x \ne -2\}\),
rango\((g) = \{y \in \mathbb{R}\ |\ y > 0\} \cup \{y \in \mathbb{R}\ |\ y \le -1\}\)

6. a)\(d(1) = 1\),,\(d(2) = 2\)\(d(3) = 2\),\(d(4) = 3\),\(d(8) = 4\),\(d(9) = 3\)
c) Los únicos números naturales\(n\) tales que\(d(n) = 2\) son los números primos. El conjunto de preimágenes del número natural 2 es el conjunto de números primos.
e)\(d(2^{0}) = 1\),\(d(2^{1}) = 2\),\(d(2^{2}) = 3\), f\(d(2^{3}) = 4\)
) Los divisores de\(2^{n}\) son\(2^{0}\),,\(2^{1}\)\(2^{2}\),...,\(2^{n - 1}\),\(2^{n}\).

7. a) El dominio de\(S\) es\(\mathbb{N}\). El conjunto de potencia de\(\mathbb{N}\),\([\mathcal{P}(\mathbb{N})]\) puede ser el codominio. La regla para determinar salidas es que para cada uno\(n \in \mathbb{N}\),\(S(n)\) es el conjunto de todos los factores numéricos naturales distintos de\(n\).
b) Por ejemplo,\(S(8) = \{1, 2, 4, 8\}\),\(S(15) = \{1, 3, 5, 15\}\).
c) Por ejemplo,\(S(2) = \{1, 2\}\),\(S(3) = \{1, 3\}\),\(S(31) = \{1, 31\}\).

Sección 6.2

1. a)\(f(0) = 4\),\(f(1) = 0\),\(f(2) = 3\),\(f(3) = 3\),\(f(4) = 0\)
b)\(g(0) = 4\),\(g(1) = 0\),\(g(2) = 3\),\(g(3) = 3\),\(g(4) = 0\)
c) Las dos funciones son iguales.

2. c) Las dos funciones no son iguales. Por ejemplo,\(f(1) = 5\) y\(g(1) = 4\).

4. (a)\(\langle a_{n} \rangle\), donde\(a_{n} = \text{cos}(n \pi)\) para cada uno\(n \in \mathbb{N}\). El dominio es\(\mathbb{N}\), y {-1, 1} puede ser el codominio. Esta secuencia es igual a la secuencia de la Parte (c).

5. (a)\(p_{1} (1, x) = 1\),\(p_{1} (1, y) = 1\),\(p_{1} (1, z) = 1\),\(p_{1} (2, x) = 2\),\(p_{1} (2, y) = 2\),\(p_{1} (2, z) = 2\)
(c) rango\((p_1) = A\), rango\((p_2) = B\)

6. Inicio del paso inductivo: Let\(P(n)\) be “Un polígono convexo con\(n\) lados tiene\(\dfrac{n(n - 3)}{2}\) diagonales”. Dejemos\(k \in D\) y supongamos que eso\(P(k)\) es cierto, es decir, un polígono convexo con\(k\) lados tiene\(\dfrac{k(k - 3)}{2}\) diagonales. Ahora deja\(Q\) ser polígono convexo con\((k + 1)\) lados. Dejar v ser uno de los\((k + 1)\) vértices de\(Q\) y let\(u\) y\(w\) ser los dos vértices adyacentes a\(v\). Al dibujar el segmento de línea desde\(u\) hasta\(w\) y omitiendo el vértice v, formamos un polígono convexo con\(k\) lados. Ahora completa el paso inductivo.

7. a)\(f(-3, 4) = 9\),\(f(-2, -7) = -23\)
b)\(\{(m, n) \in \mathbb{Z} \times \mathbb{Z}\ |\ m = 4 - 3n\}\)

9. (a) det\(\left [{\begin{array} {cc} 3 & 5 \\ 4 & 1\\ \end{array}} \right]\) = -17, det\(\left [{\begin{array} {cc} 1 & 0 \\ 0 & 7\\ \end{array}} \right]\) = 7 y det\(\left [{\begin{array} {cc} 3 & -2 \\ 5 & 0\\ \end{array}} \right]\) = 10.

Sección 6.3

2. (a) La función no\(f\) es una inyección y no es una sobreyección.
(c) La función\(F\) es una inyección y es una sobreyección.

3. (a) La función\(f\) es una inyección y no es una sobreyección.
b) La función\(F\) es una inyección y es una sobreyección.

4. (a) Dejar\(F: \mathbb{R} \to \mathbb{R}\) ser definido por\(F(x) = 5x + 3\) para todos\(x \in \mathbb{R}\). Dejemos\(x_1, x_2 \in \mathbb{R}\) y asumamos eso\(F(x_1) = F(x_2)\). Entonces\(5x_1 + 3 = 5x_2 + 3\). Demostrar que esto implica eso\(x_1 = x_2\) y, por lo tanto,\(F\) es una inyección.
Ahora vamos\(y \in \mathbb{R}\). Entonces\(\dfrac{y - 3}{5} \in \mathbb{R}\). \(F(\dfrac{y - 3}{5}) = y\)Demuéstralo. Así,\(F\) es una sujeción y por lo tanto\(F\) es una bijección.
(b) Notar que para cada uno\(x \in \mathbb{Z}\),\(G(x) \equiv 3\) (mod 5). Ahora explique por qué no\(G\) es una sobrejección.

7. La función de cumpleaños no es una inyección ya que hay dos personas diferentes con el mismo cumpleaños. La función de cumpleaños es una sobrejección ya que por cada día del año, hay una persona que nació ese día.

9. (a) La función\(f\) es una inyección y una sobreyección.
b) La función\(g\) es una inyección y no es una sobreyección.

Sección 6.4

3. a)\(F(x) = (g \circ f) (x)\),\(f(x) = e^{x}\),\(g(x) = \text{cos} x\)
b)\(G(x) = (g \circ f) (x)\)\(f(x) = \text{cos} x\),\(g(x) = e^{x}\)

4. (a) Para cada uno\(x \in A\). \((f \circ I_{A}) (x) = f(I_{A}(x)) = f(x)\). Por lo tanto,\(f \circ I_{A} = f\).

5. a)\([(h \circ g) \circ f] (x) = \sqrt[3]{\text{sin}(x^2)}\);\([h \circ (g \circ f)](x) \sqrt[3]{\text{sin}(x^2)}\)

6. Inicio de una prueba: Dejar\(A\),\(B\), y\(C\) ser conjuntos no vacíos y dejar\(f: A \to B\) y\(g: B \to C\). Supongamos que\(f\) y\(g\) son ambas inyecciones. Dejemos\(x, y \in A\) y asumamos eso\((g \circ f)(x) = (g \circ f)(y)\).

7. (a)\(f: \mathbb{R} \to \mathbb{R}\) por\(f(x) = x\),\(g: \mathbb{R} \to \mathbb{R}\) por\(g(x) = x^2\). La función\(f\) es una sobreyección, pero no\(g \circ f\) es una sobreyección.
(f) Por la Parte (1) del Teorema 6.21, esto no es posible ya que si\(g \circ f\) es una inyección, entonces\(f\) es una inyección.

Sección 6.5

2. b)\(f^{-1} = \{(c, a), (b, b), (d, c), (a, d)\}\)
d)\((f^{-1} \circ f) (x) = x = (f \circ f^{-1}) (x)\). Esto ilustra el Corolario 6.28.

4. Usando la notación de Corolario 6.28, si\(y = f(x)\) y\(x = f^{-1}(y)\), entonces

\(\begin{array} {rcl} {(f \circ f^{-1} (y)} &= & {f(f^{-1} (y))} \\ {} &= & {f(x)} \\ {} &= & {y} \end{array}\)

6. (a) Que\(x, y \in A\) y asuma eso\(f(x) = f(y)\). Aplicar\(g\) a ambos lados de esta ecuación para demostrarlo\((g \circ f)(x) = (g \circ f)(y)\). Ya que\(g \circ f = I_{A}\), esto implica que\(x = y\) y de ahí que\(f\) sea una inyección.
(b) Empezar asumiendo eso\(f \circ g = I_{B}\), y luego dejar\(y \in B\). Hay que demostrar que existe\(x \in A\) tal eso\(f(x) = y\).
d)\(g: \mathbb{R}^{+} \to \mathbb{R}\) por\(g(y) = \dfrac{1}{2}(\text{In} y + 1)\)

7. La inversa de no\(f\) es una función y la inversa de\(g\) es una función.

Sección 6.6

1. (a) Existe\(x \in A \cap B\) tal que\(f(x) = y\).
d) Existe\(a \in A\) tal que\(f(a) = y\) o existe\(b \in B\) tal que\(f(b) = y\).
f) h\(f(x) \in C \cup D\)
)\(f(x) \in C\) o\(f(x) \in D\).

2. b)\(f^{-1} (f(A)) = [2, 5]\).
e)\(f(A \cap B) = [-5, -3]\)
d\(f(f^{-1}(C)) = [-2, 3]\)
) f)\(f(A) \cap f(B) = [-5, -3]\)

3. a\(g(A \times A) = \{6, 12, 18, 24, 36, 54, 72, 108, 216\}\)
) b\(g^{-1} (C) = \{(1, 1), (2, 1), (1, 2)\}\)

4. (a) rango\((F) = F(S) = \{1, 4, 9, 16\}\)

5. Para probarlo\(f(A \cup B) \subseteq f(A) \cup f(B)\), empieza por dejar\(y \in f(A \cup B)\). Esto quiere decir que existe un\(x\) en\(A \cup B\) tal que\(f(x) = y\). ¿Cómo lo demuestras\(y \in f(A) \cup f(B)\)?

6. Para probarlo\(f^{-1} (C \cap D) \subseteq f^{-1}(C) \cap f^{-1}(D)\), vamos\(x \in f^{-1} (C \cap D)\). Entonces\(f(x) \in C \cap D\). ¿Cómo lo demuestras\(x \in f^{-1}(C) \cap f^{-1}(D)\)?

9. La declaración (a) es verdadera y la Declaración (b) es falsa.

Sección 7.1

1. (a) El conjunto\(A \times B\) contiene nueve pares ordenados. El conjunto\(A \times B\) es una relación de\(A\) a\(B\) ya que\(A \times B\) es un subconjunto de\(A \times B\).
b) El conjunto\(R\) es una relación desde\(A\) hasta\(B\) desde\(R \subseteq A \times B\).
(c) dom\((R) = A\), rango\((R) = \{p, q\}\)
(d)\(R^{-1} = \{(p, a), (q, b), (p, c), (q, a)\}\)

2. Sólo es verdadera la afirmación de la Parte (b).

3. (a) El dominio de\(D\) consiste en las ciudadanas de Estados Unidos cuya madre es ciudadana femenina de los Estados Unidos.
(b) El rango de\(D\) consiste en aquellas ciudadanas de Estados Unidos que tienen una hija que es ciudadana femenina de los Estados Unidos.

4. (a)\((S, T) \in R\) significa que\(S \subseteq T\).
(b) El dominio de la relación de subconjunto es\(\mathcal{P}(U)\).
(c) El rango del subsetr elation es\(\mathcal{P}(U)\).
d)\(R^{-1} = \{(T, S) \in \mathcal{P}(U) \times \mathcal{P}(U)\ |\ S \subseteq T\}\).
(e) La relación no\(R\) es una función de\(\mathcal{P}(U)\) a\(\mathcal{P}(U)\) ya que cualquier subconjunto apropiado de\(U\) es un subconjunto de más de un subconjunto de\(U\).

6. (a)\(\{x \in \mathbb{R}\ |\ (x, 6) \in S\} = \{-8, 8\}\)
\(\{x \in \mathbb{R}\ |\ (x, 9) \in S\} = \{-\sqrt{19}, \sqrt{19}\}\)
(b) El dominio y rango de\(S\) es el intervalo cerrado [-10, 10].
d) La relación no\(S\) es una función de\(\mathbb{R}\) a\(\mathbb{R}\).

9. (a)\(R = \{(a, b) \in \mathbb{Z} \times \mathbb{Z}\ |\ |a - b| \le 2\}\)
(b) dom\((R) = \mathbb{Z}\) y rango\((R) = \mathbb{Z}\)

Sección 7.2

1. La relación no\(R\) es reflexiva\(A\) y no es simétrica. No obstante, es transitiva ya que la declaración condicional “Para todos\(x, y, z \in A\), si\(x\ R\ y\) y\(y\ R\ z\), entonces\(x\ R\ z\)" es una declaración condicional verdadera.

4. La relación no\(R\) es reflexiva\(A\), es simétrica y no transitiva.

6. a) La relación\(\sim\) es una relación de equivalencia.
b)\(C = \{-5, 5\}\)

10. La relación\(\sim\) es una relación de equivalencia y la relación no\(\thickapprox\) es una relación de equivalencia.

15. (c) El conjunto\(C\) es un círculo de radio 5 con el centro en el origen.

Sección 7.3

1. \([a] = [b] = \{a, b\}\);\([c] = \{c\}\);\([d] = [e] = \{d, e\}\)

2. \([a] = [b] = [d] = \{a, b, d\}\);\([c] = \{c\}\);\([e] = [f] = \{e, f\}\)

3. Las clases de equivalencia son {0, 1, 2,..., 9}, {10, 11, 12,..., 99}, {100, 101, 102,..., 999}, {1000}.

4. Las clases de congruencia para la relación de congruencia módulo 5 en el conjunto de enteros son

\([0] = \{5n\ |\ n \in \mathbb{Z}\)\([3] = \{5n + 3\ |\ n \in \mathbb{Z}\)
\([1] = \{5n + 1\ |\ n \in \mathbb{Z}\)
\([2] = \{5n + 2\ |\ n \in \mathbb{Z}\)\([4] = \{5n + 4\ |\ n \in \mathbb{Z}\)

5. (a) Las distintas clases de equivalencia son {0, 3, 6}, {1, 8}, {2, 7} y {4, 5}.

6. (a) Dejar\(x \in [\dfrac{5}{7}]\). Entonces\(x - \dfrac{5}{7} \in \mathbb{Z}\), lo que significa que hay un entero\(m\) tal que\(x - \dfrac{5}{7} = m\), o\(x = \dfrac{5}{7} + m\). Esto prueba eso\(x \in \{m + \dfrac{5}{7}\ |\ m \in \mathbb{Z}\}\) y, por lo tanto, eso\([\dfrac{5}{7}] \subseteq \{m + \dfrac{5}{7}\ |\ m \in \mathbb{Z}\}\). Todavía tenemos que demostrar que\(\{m + \dfrac{5}{7}\ |\ m \in \mathbb{Z}\} \subseteq [\dfrac{5}{7}]\)

9. (a) Para probar que la relación es simétrica, tenga en cuenta que si\((a, b) \thickapprox (c, d)\), entonces\(ad = bc\). Esto implica que\(cb = da\) y, por lo tanto,\((c, d) \thickapprox (a, b)\)
c\(3a = 2b\)

Sección 7.4

1. a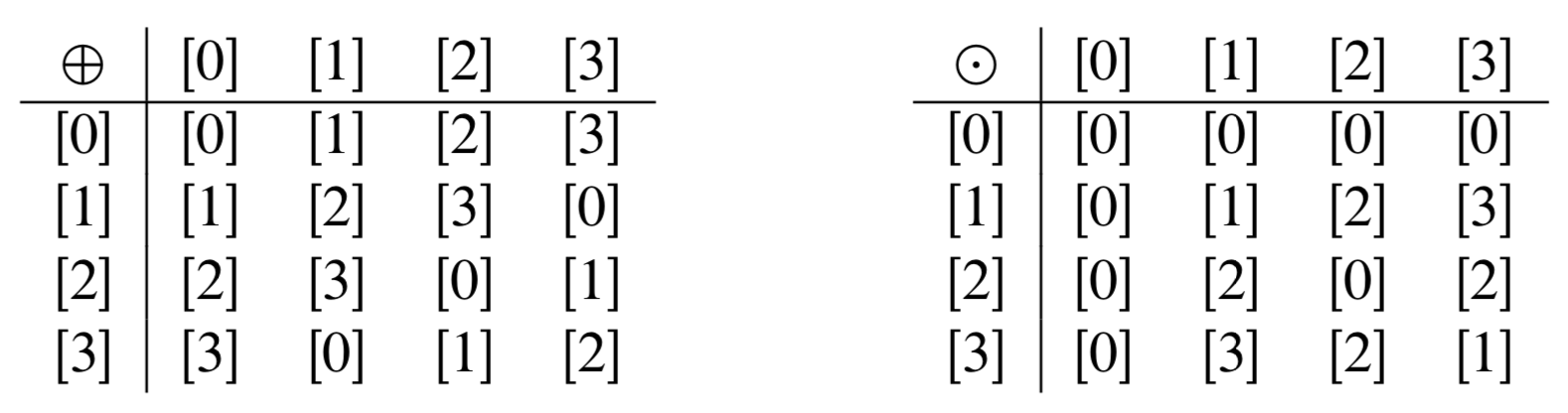
) b

2. (a)\([x] = [1]\) o\([x] = [3]\)
(e)\([x] = [2]\) o\([x] = [3]\)
(g) La ecuación no tiene solución.

3. El enunciado en (a) es falso. El enunciado en (b) es cierto.

5. a) La prueba consta de los siguientes cómputos:

\(\begin{array} {lcl} {[1]^1 = [1]} & & {[3]^1 = [9] = [4]} \\ {[2]^1 = [4]} & & {[4]^1 = [16] = [1].} \end{array}\)

17. a) Demostrar el contrapostivo calculando\([a]^2 + [b]^2\) para todos los distintos de cero\([a]\) y\([b]\) en\(\mathbb{Z}_3\).

Sección 8.1

1. (a) gcd (21, 28) = 7
(b) gcd (-21, 28) = 7
(c) gcd (58, 63) = 1
(d) gcd (0, 12) = 12

2. (a) Pista: Demuéstralo\(k\ |\ [(a + 1) - a]\).

4. (a)\(|b|\) es el mayor número natural que divide 0 y\(b\).
b) Los enteros\(b\) y\(-b\) tienen los mismos divisores. Por lo tanto,\(\text{gcd}(a, -b) = \text{gcd}(a, b)\).

5. (a) gcd (36, 60) = 12\(12 = 36 \cdot 2 + 60 \cdot (-1)\)
(a) gcd (901, 935) = 17\(17 = 901 \cdot 27 + 935 \cdot (-26)\)
(a) gcd (901, -935) = 17\(17 = 901 \cdot 27 + (-935) \cdot (26)\)

7. a\(11 \cdot (-3) + 17 \cdot 2 = 1\)
) b\(\dfrac{m}{11} + \dfrac{n}{17} = \dfrac{17m + 11n}{187}\)

Sección 8.2

1. Los únicos divisores de número natural de un número primo\(p\) son 1 y\(p\).

2. Casos de uso: (1)\(p\) divide\(a\); (2) p no divide\(a\). En este caso, use el hecho de que gcd (\(a\),\(p\)) = 1 para escribir el número 1 como una combinación lineal de\(a\) y\(p\).

3. Un indicio para el paso inductivo: Escribir\(p\ |\ (a_{1} a_{2} \cdot\cdot\cdot a_{m})a_{m + 1}\). Entonces mira dos casos: (1)\(p\ |\ a_{m + 1}\); (2)\(p\) no divide\(a_{m + 1}\).

4. (a) gcd (\(a\),\(b\)) = 1. ¿Por qué?
(b) gcd (\(a\),\(b\)) = 1 o gcd (\(a\),\(b\)) = 1=2. ¿Por qué?

7. (a) gcd (16, 28) = 4. Además,\(\dfrac{16}{4} = 4\),\(\dfrac{28}{4} = 7\), y gcd (4, 7) = 1.

9. La parte (b) del Ejercicio (8) puede ser útil.

11. El enunciado es cierto. Inicio de una prueba: Si gcd (\(a\),\(b\)) = 1 y\(c\ |\ (a + b)\), entonces existen enteros\(x\) y\(y\) tal que\(ax + by = 1\) y existe un entero m tal que\(a + b = cm\).

Sección 8.3

3. a)\(x = -3 + 14k, y = 2 - 9k\)
b)\(x = -1 + 11k, y = 1 + 9k\)
c) Sin solución
d\(x = 2 + 3k, y = -2 - 4k\)

4. Existen varias soluciones posibles a este problema, cada una de las cuales se puede generar a partir de las soluciones de la ecuación Diofantina\(27x + 50y = 25\).

5. Este problema se puede resolver encontrando todas las soluciones de una ecuación Diofantina lineal en\(x\) y\(y\), donde ambos\(x\) y\(y\) son positivos. El número mínimo de personas que asisten al banquete es de 66.

6. a)\(y = 12 + 16k\),\(x_3 = -1 - 3k\)
c)\(x_1 = y + 3n\),\(x_2 = -y + 4n\)

Sección 9.1

2. Utilizar\(f: A \times \{x\} \to A\) por\(f(a, x) = a\), para todos\((a, x) \in A \times \{x\}\).

4. Observe eso\(A = (A - \{x\}) \cup \{x\}\). Utilice el Teorema 9.6 para concluir que\(A - \{x\}\) es finte. Después usa Lemma 9.4.

5. (a) Ya que\(A \cap B \subseteq A\), si\(A\) es finito, entonces el Teorema 9.6 implica que\(A \cap B\) es finito.

7. (a) Recuerde que dos pares ordenados son iguales si y sólo si sus coordenadas correspondientes son iguales. Entonces si\(h(a_1, c_1) = h(a_2, c_2)\), entonces\((f(a_1), g(c_1)) = (f(a_2), g(c_2))\). Entonces podemos concluir que\(f(a_1) = f(a_2)\) y\(g(c_1) = g(c_2)\).

8. (a) Si definimos la función\(f\) por\(f(1) = a\),\(f(2) = b\)\(f(3) = c\),\(f(4) = a\),, y\(f(5) = b\), entonces podemos usar\(g(a) = 1\),\(g(b) = 1\), y\(g(3) = c\). La función\(g\) es una inyección.

Sección 9.2

1. Todos excepto la Parte (d) son verdaderos.

2. e) Definir una biyección apropiada o utilizar el Corolario 9.20 para concluir que\(\mathbb{N} - \{4, 5, 6\}\) es contable. Demostrar que\(\mathbb{N} - \{4, 5, 6\}\) no puede ser finito.
f)\(\{m \in \mathbb{Z}\ |\ m \equiv 2 \text{ (mod 3)}\} = \{3k + 2\ |\ k \in \mathbb{Z}\}\)

5. Para cada uno\(n \in \mathbb{N}\), deja\(P(n)\) ser “Si carta (\(B\)) =\(n\), entonces\(A \cup B\) es un conjunto contablemente infinito”.

Tenga en cuenta que si tarjeta\((B) = k + 1\) y\(x \in B\), luego tarjeta\((B - \{x\}) = k\). Aplicar la suposición inductiva a\(B - \{x\}\).

6. Observe que si\(h(n) = h(m)\), entonces desde\(A\) y\(B\) son disjuntos, cualquiera\(h(n)\) y\(h(m)\) están ambos en\(A\) o están ambos en\(B\).

También, si\(y \in A \cup B\), entonces sólo hay dos casos a considerar:\(y \in A\) o\(y \in B\).

8. Ya que\(A - B \subseteq A\), el conjunto\(A - B\) es contable. Ahora supongamos que\(A - B\) es finte y demuestra que esto lleva a una contradicción.

Sección 9.3

1. (a)\(f: (0, \infty) \to \mathbb{R}\) por\(f(x) = \text{In} x\) para todos\(x \in (0, \infty)\)
(b)\(g: (0, \infty) \to (a, \infty)\) por\(g(x) = x + a\) para todos\(x \in (0, \infty)\). La función\(g\) es una biyección y así\((0, \infty) \thickapprox (a, \infty)\). Luego use la Parte (a).

2. Mostrar que la suposición de que el conjunto de números irracionales es contable conduce a una contradicción.

3. Utilice Corolario 9.20.