2.1: Predicados y Conectivos Lógicos
- Page ID
- 114068
En cada rama de las Matemáticas hay nociones especiales, atómicas, que desafían la definición precisa. En Geometría, por ejemplo, las nociones atómicas son puntos, líneas y su incidencia. Euclides define un punto como “aquello que no tiene parte” —la gente puede argumentar (y haber argumentado) incesantemente sobre qué se entiende exactamente con esto. ¿Está diciendo esencialmente que cualquier cosa sin volumen, área o longitud de algún tipo es un punto? En los tiempos modernos se ha reconocido que cualquier sistema formal de argumentación tiene que tener conceptos tan elementales, indefinidos —y que el aparente lapso de precisión de Euclides proviene de un intento de ocultar este hecho básico. La noción de “punto” no puede definirse realmente. Todo lo que podemos hacer es señalar (sin intención de broma) una variedad de puntos y esperar que nuestro público absorba el mismo concepto de punto que sostenemos a través del proceso de inducción 1.
Los conceptos atómicos en la Teoría de Conjuntos son “set”, “element” y “membership”. Los conceptos atómicos en Lógica son “verdadero”, “falso”, “oración” y “declaración”.
En cuanto a lo verdadero y a lo falso, esperamos que no haya incertidumbre en cuanto a sus significados. La oración también tiene un significado bien entendido en el que la mayoría estará de acuerdo: una colección ordenada sintácticamente correcta de palabras como “Johnny era jugador de fútbol” o “El rojo es un color” o “Esta es una oración que no se refiere a sí misma”. Una declaración es una oración que es verdadera o falsa. En otras palabras, una declaración es una oración cuyo valor de verdad es definitivo, en otras palabras, siempre es posible decidir —de una forma u otra— si una declaración es verdadera o falsa. 2 El primer ejemplo de una frase dada anteriormente (“Johnny era jugador de fútbol”) no es una declaración — el problema es que es ambigua a menos que sepamos quién es Johnny. Si hubiera dicho “Johnny Unitas era jugador de fútbol”. entonces habría sido una declaración. Si hubiera dicho “Johnny Appleseed era un futbolista”. también habría sido una declaración, simplemente no una verdadera.
La ambigüedad es sólo una razón por la que una sentencia puede no ser una declaración. Al considerar oraciones más complejas, puede darse el caso de que el valor de verdad de una sentencia dada simplemente no pueda decidirse. Uno de los resultados matemáticos más celebrados del\(20^{\text{th}}\) siglo es el “Teorema de Incompletitud” de Kurt Gödel. Un aspecto importante de esta teoría es la prueba de que en cualquier sistema axiomático de pensamiento matemático debe haber oraciones indecibles —afirmaciones que no pueden probarse ni desmentirse de los axiomas 3. Las oraciones simples (por ejemplo, las de la forma sujeto-verbo-objeto) tienen pocas posibilidades de ser indecibles por esta razón, por lo que a continuación veremos formas de construir oraciones más complejas a partir de componentes simples.
Empecemos con un ejemplo. Supongamos que me acerco a ti en alguna habitación sin ventanas y hago la declaración: “¡El sol brilla pero está lloviendo!” Usted decide investigar mi afirmación y determinar su veracidad. Al llegar a una habitación que tiene vista al exterior hay cuatro posibles combinaciones de sol y/o precipitación que puede encontrar. Es decir, los predicados atómicos “El sol brilla” y “Está lloviendo” pueden ser cada uno verdadero o falso independientemente el uno del otro. En la siguiente tabla presentamos una convención utilizada a lo largo del resto de este libro —que true se indica con mayúscula\(\text{T}\) y false se indica con la letra griega\(\phi\) (que básicamente es griega\(\text{F}\), y es mucho más difícil confundir con una\(\text{T}\) que una \(\text{F}\)es.)
| El sol brilla | Está lloviendo |
|---|---|
| \(\text{T}\) | \(\text{T}\) |
| \(\text{T}\) | \(\phi\) |
| \(\phi\) | \(\text{T}\) |
| \(\phi\) | \(\phi\) |
Cada fila de la tabla anterior representa un posible estado del mundo exterior. Supongamos que observa las condiciones dadas en la última fila, es decir, que no es ni soleado, ni llueve —sin duda concluirías que no soy de confiar en mí. Es decir, mi afirmación, la composición de “El sol brilla” y “Está lloviendo” (con la palabra “pero” en el medio como conector) es falsa. Si lo piensas un poco, estarás de acuerdo en que esta llamada oración compuesta es cierta solo en el caso de que ambas piezas componentes sean ciertas. Esto subraya un punto lingüístico entretenido: ¡“pero” y “y” tienen exactamente el mismo significado! Más precisamente, denotan lo mismo, tienen connotaciones sutilmente distintas sin embargo —“ pero” indica que ambas declaraciones que conecta son ciertas y que el orador se sorprende por este estado de cosas.
En Matemáticas distinguimos dos conectivos principales para conectar oraciones simples en compuestas. La conjunción de dos oraciones es la oración compuesta hecha pegando la palabra “y” entre ellas. La disyunción de dos oraciones se forma colocando una “o” entre ellas. Las conjunciones son verdaderas solo cuando ambos componentes son verdaderos. Las disyunciones son falsas solo cuando ambos componentes son falsos.
Como es habitual, los matemáticos han desarrollado una notación increíblemente concisa y compacta para estas ideas. 4 Primero, representamos una oración completa por una sola letra —tradicionalmente, una letra mayúscula. A esto se le llama variable predicado. Por ejemplo, siguiendo el ejemplo anterior, podríamos denotar la frase “El sol brilla” por la letra\(\text{S}\). De igual manera, podríamos hacer la tarea\(\text{R} =\) “Está lloviendo”. La conjunción y disyunción de estas oraciones pueden representarse entonces usando los símbolos\(S ∧ R and \(S ∨ R\), respectivamente. Como mnemotécnico, tenga en cuenta que el conectivo en\(S ∧ R\) se parece mucho a la letra mayúscula\(\text{A}\) (como en Y).
Para mostrar, de manera muy sucinta, el efecto de estas dos conectivas podemos utilizar las llamadas tablas de verdad. En una tabla de verdad, enumeramos todos los valores de verdad posibles de las variables predicadas y luego enumeramos los valores de verdad de alguna oración compuesta. Para los conectores de conjunción y disyunción tenemos (respectivamente):
| \(A\) | \(B\) | \(A ∧ B\) |
|---|---|---|
| \ (A\) ">\(\text{T}\) | \ (B\) ">\(\text{T}\) | \ (A B\) ">\(\text{T}\) |
| \ (A\) ">\(\text{T}\) | \ (B\) ">\(\phi\) | \ (A B\) ">\(\phi\) |
| \ (A\) ">\(\phi\) | \ (B\) ">\(\text{T}\) | \ (A B\) ">\(\phi\) |
| \ (A\) ">\(\phi\) | \ (B\) ">\(\phi\) | \ (A B\) ">\(\phi\) |
y
| \(A\) | \(B\) | \(A ∨ B\) |
|---|---|---|
| \ (A\) ">\(\text{T}\) | \ (B\) ">\(\text{T}\) | \ (A... B\) ">\(\text{T}\) |
| \ (A\) ">\(\text{T}\) | \ (B\) ">\(\phi\) | \ (A... B\) ">\(\text{T}\) |
| \ (A\) ">\(\phi\) | \ (B\) ">\(\text{T}\) | \ (A... B\) ">\(\text{T}\) |
| \ (A\) ">\(\phi\) | \ (B\) ">\(\phi\) | \ (A... B\) ">\(\phi\) |
Además de estos conectores necesitamos un modificador (llamado negación) que actúe sobre oraciones individuales. La negación de una oración\(A\) se denota por\(¬A\), y su valor de verdad es exactamente lo opuesto al valor\(A\) de la verdad de su. La negación de una sentencia también se conoce como la negación de una sentencia. Una tabla de verdad para el operador de negación es algo trivial pero la incluimos aquí para que sea completa.
| \(A\) | \(¬A\) |
|---|---|
| \ (A\) ">\(\text{T}\) | \ (¬A\) ">\(\phi\) |
| \ (A\) ">\(\phi\) | \ (¬A\) ">\(\text{T}\) |
Estas tres herramientas simples (y, o & no) son suficientes para crear oraciones extraordinariamente complejas a partir de componentes básicos. La forma en que estas piezas se interrelacionan recuerda un poco al álgebra, de hecho, el estudio de estos operadores lógicos (o cualquier operador que actúe como ellos) se llama Álgebra booleana 5. Sin embargo, existen diferencias distintas entre álgebra booleana y ordinaria. En álgebra regular tenemos los conectores binarios\(+\) (plus) y\(·\) (times), y el operador de negación unaria\(−\), estos son ciertamente análogos a\(∧\),\(∨\) &\(¬\), pero hay ciertas consecuencias del hecho de que la multiplicación se repite efectivamente suma que simplemente no se sostienen para los operadores booleanos. Por ejemplo, hay una precedencia bien definida entre\(·\) y\(+\). Al analizar la expresión todos\(4 · 5 + 3\) sabemos que la multiplicación se debe hacer primero. No existe tal regla que rija el orden de operaciones entre\(∧\) y\(∨\), entonces una expresión como\(A ∧ B ∨ C\) es simplemente ambigua —debe tener paréntesis insertados para mostrar el orden, ya sea\((A∧B)∨C\) o\(A∧(B∨C)\). Otra distinción entre álgebra ordinaria y booleana es la exponenciación. Si hubiera exponentes en el álgebra booleana, necesitaríamos dos tipos diferentes: uno para conjunción repetida y otro para disyunción repetida.
¿Por qué es que no existe tal cosa como la exponenciación en el álgebra de la Lógica?
Si bien hay muchas diferencias entre el álgebra booleana y el álgebra habitual, de variedades de jardín, también hay muchas similitudes. Por ejemplo, las leyes asociativas, conmutativas y distributivas del Álgebra tienen todas versiones que funcionan en el caso booleano.
Una forma muy práctica de visualizar expresiones booleanas viene dada por los diagramas de circuito lógico digital. Para discutir estos diagramas debemos hacer una breve digresión hacia la Electrónica. Uno de los componentes más básicos dentro de un dispositivo electrónico es un transistor, este es un componente que actúa como un interruptor para la electricidad, pero el interruptor en sí está controlado por la electricidad. En la Figura\(2.1.1\) vemos la representación esquemática habitual de un transistor. Si se aplica voltaje al cable etiquetado\(\text{z}\), el transistor se vuelve conductor y la corriente puede fluir de\(\text{x}\) a\(\text{y}\).
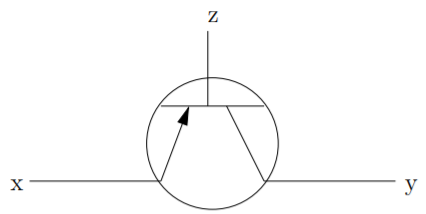
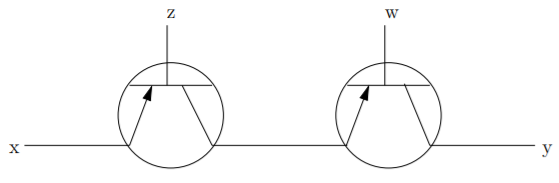
Supongamos que dos transistores están conectados como en la Figura\(2.1.2\) (esto se llama conexión en serie). Para que la corriente fluya de\(\text{x}\) a\(\text{y}\) debemos tener voltaje aplicado tanto a los cables etiquetados como\(\text{z}\) a\(\text{w}\). En otras palabras, este circuito crea efectivamente la operación y — suponiendo que siempre se aplique voltaje a\(\text{x}\), si\(z\) y\(\text{w}\) se energizan entonces la salida a\(\text{y}\) será energizada.
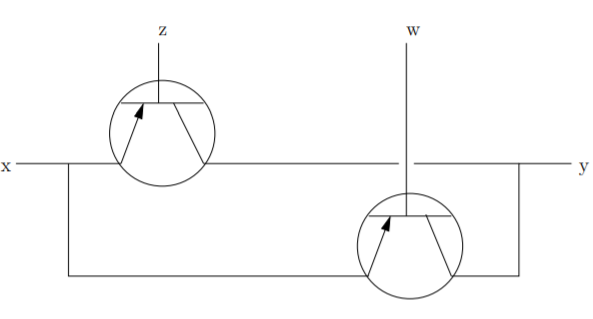
Cuando dos transistores están conectados en paralelo (esto se ilustra en la Figura\(2.1.3\)) la corriente puede fluir desde\(\text{x}\) hasta\(\text{y}\) cuando cualquiera (o ambos) de los cables en\(\text{z}\) y\(\text{w}\) tienen voltaje aplicado. Esto trae a colación un punto que resulta confuso para algunos: en el habla común el uso de la palabra “o” a menudo tiene el sentido conocido como exclusivo o (a.k.a. xor), cuando decimos “\(\text{X}\)o\(\text{Y}\)” nos referimos a “O X o Y, pero no ambos”. En Electrónica y Matemáticas, o siempre tiene el sentido no exclusivo (más conocido como inclusivo).
Como una especie de taquigrafía gráfica, los ingenieros electrónicos utilizan los símbolos a continuación para indicar puertas y, puertas o y no puertas (más conocidas como negadores).
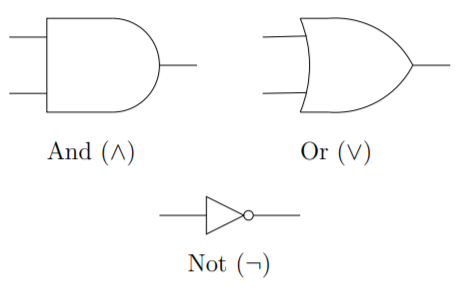
Una puerta y tiene dos transistores en su interior que están cableados en serie; si ambas entradas están energizadas, la salida también lo estará. Una puerta o puerta tiene dos transistores en paralelo en su interior. Las no-puertas implican magia —cuando su entrada no está encendida, su salida es y viceversa.
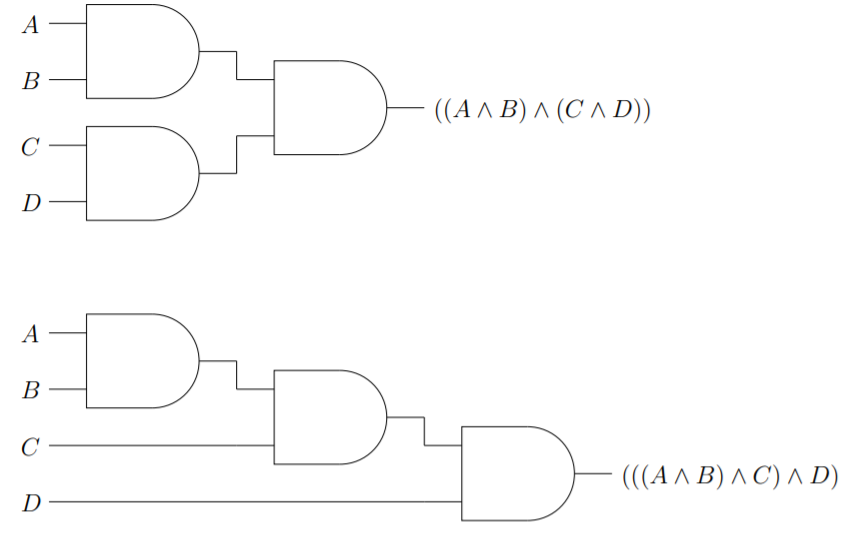
Usando este “lenguaje” gráfico se pueden hacer representaciones esquemáticas de expresiones lógicas. Algunos encuentran que rastrear tales diagramas facilita la comprensión de la estructura de una expresión booleana. Por ejemplo, en la Figura\(2.1.4\) ilustramos\(2\) las posibles formas en que la conjunción de cuatro variables predicadas puede estar entre paréntesis. De hecho, cuando una multitud de predicados se unen por el mismo conectivo, la forma en que la expresión está entre paréntesis no es importante, por lo que a menudo se ve una taquigrafía adicional: puertas con más que\(2\) entradas.
Una tarea común para un diseñador de electrónica es crear un circuito lógico digital que tenga una tabla de entrada/salida prescrita. Tenga en cuenta que una tabla de entrada/salida para un circuito lógico es completamente análoga a una tabla de verdad para una oración compuesta en Lógica, excepto que usamos\(0\)'s y\(1\)'s en lugar\(\text{T}\) de's y\(\phi\)'s.
Supongamos que quisiéramos diseñar un circuito que tuviera la siguiente tabla de entrada/salida.
| \(x\) | \(y\) | \(z\) | \(\text{out}\) |
|---|---|---|---|
| \ (x\) ">\(0\) | \ (y\) ">\(0\) | \ (z\) ">\(0\) | \ (\ text {out}\) ">\(0\) |
| \ (x\) ">\(0\) | \ (y\) ">\(0\) | \ (z\) ">\(1\) | \ (\ text {out}\) ">\(0\) |
| \ (x\) ">\(0\) | \ (y\) ">\(1\) | \ (z\) ">\(0\) | \ (\ text {out}\) ">\(0\) |
| \ (x\) ">\(0\) | \ (y\) ">\(1\) | \ (z\) ">\(1\) | \ (\ text {out}\) ">\(1\) |
| \ (x\) ">\(1\) | \ (y\) ">\(0\) | \ (z\) ">\(0\) | \ (\ text {out}\) ">\(0\) |
| \ (x\) ">\(1\) | \ (y\) ">\(0\) | \ (z\) ">\(1\) | \ (\ text {out}\) ">\(0\) |
| \ (x\) ">\(1\) | \ (y\) ">\(1\) | \ (z\) ">\(0\) | \ (\ text {out}\) ">\(1\) |
| \ (x\) ">\(1\) | \ (y\) ">\(1\) | \ (z\) ">\(1\) | \ (\ text {out}\) ">\(1\) |
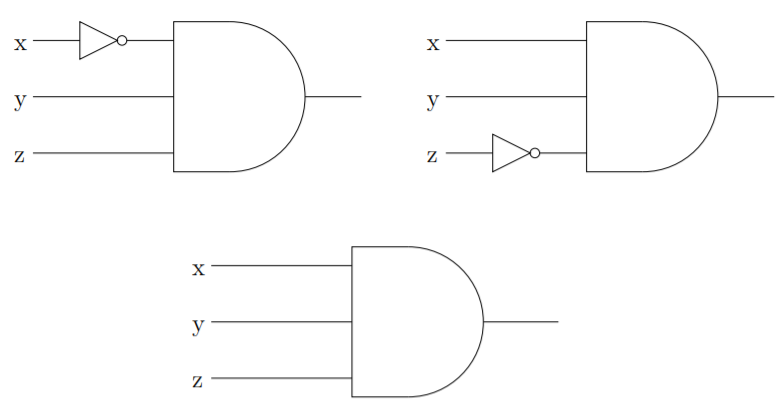
Un método sistemático para llevar a cabo tal tarea de diseño implica una noción llamada forma normal disyuntiva. Una expresión booleana está en forma normal disyuntiva si consiste en la disyunción de una o más declaraciones, cada una de las cuales consiste enteramente en conjunciones de variables predicadas y/o sus negaciones. En otras palabras, el o de un montón de ands. En cuanto a los circuitos lógicos digitales, los ands de los que estamos hablando se llaman reconocedores. Por ejemplo, los siguientes\(3\) -input y-gates reconocen los estados de entrada en las\(8^{\text{th}}\) filas\(4^{\text{th}}\),\(7^{\text{th}}\) y de la tabla de E/S anterior. (Estas son las filas donde se supone que debe estar la salida\(1\).)
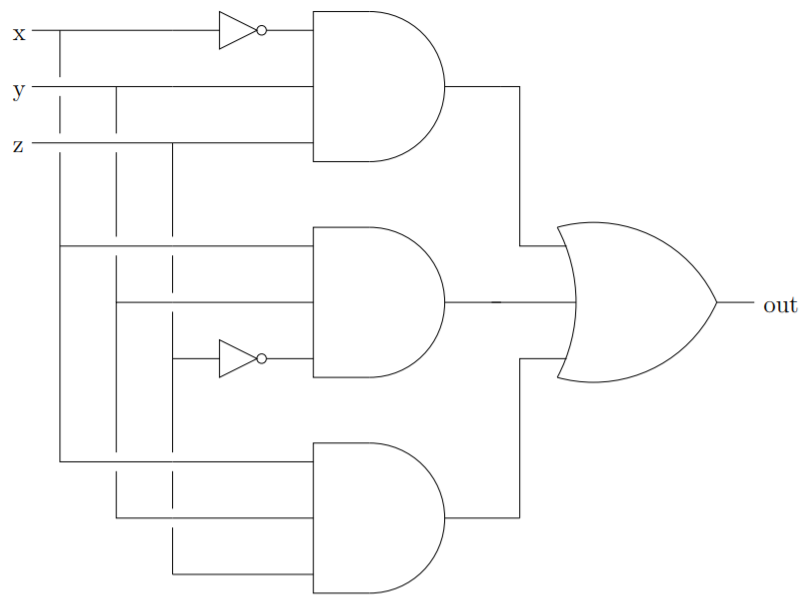
En la Figura\(2.1.5\) ilustramos cómo crear un circuito cuya tabla de E/S es la anterior usando estos reconocedores.
Ejercicios
Diseñe un circuito lógico digital (usando y, o & no puertas) que implemente un exclusivo o
Considerar la frase “Esta es una oración que no se refiere a sí misma”. que se dio al inicio de este capítulo como ejemplo. ¿Esta frase es una declaración? Si es así, ¿cuál es su valor de verdad?
Considera la frase “Esta frase es falsa”. ¿Esta frase es una declaración?
Tablas completas de verdad para cada una de las oraciones\((A∧B)∨C\) y\(A∧(B∨ C)\). ¿Parece que estas frases tienen el mismo contenido lógico?
Hay otras dos conectivas lógicas que se usan algo menos comúnmente que\(∨\) y\(∧\). Se trata del trazo de Scheffer y la flecha de Peirce —escrita\(|\) y\(↓\), respectivamente— también se les conoce como NAND y NOR.
Las tablas de verdad para estos conectivos son:
| \(A\) | \(B\) | \(A|B\) |
|---|---|---|
| \ (A\) ">\(\text{T}\) | \ (B\) ">\(\text{T}\) | \ (A|B\) ">\(\phi\) |
| \ (A\) ">\(\text{T}\) | \ (B\) ">\(\phi\) | \ (A|B\) ">\(\text{T}\) |
| \ (A\) ">\(\phi\) | \ (B\) ">\(\text{T}\) | \ (A|B\) ">\(\text{T}\) |
| \ (A\) ">\(\phi\) | \ (B\) ">\(\phi\) | \ (A|B\) ">\(\text{T}\) |
y
| \(A\) | \(B\) | \(A↓B\) |
|---|---|---|
| \ (A\) ">\(\text{T}\) | \ (B\) ">\(\text{T}\) | \ (A18" B\) ">\(\phi\) |
| \ (A\) ">\(\text{T}\) | \ (B\) ">\(\phi\) | \ (A18" B\) ">\(\phi\) |
| \ (A\) ">\(\phi\) | \ (B\) ">\(\text{T}\) | \ (A18" B\) ">\(\phi\) |
| \ (A\) ">\(\phi\) | \ (B\) ">\(\phi\) | \ (A18" B\) ">\(\text{T}\) |
Encuentra una expresión para\((A ∧ ¬B) ∨ C\) usar solo estas nuevas conectivas (así como la negación y los propios símbolos variables)
El famoso lógico Raymond Smullyan ideó una familia de acertijos lógicos alrededor de un lugar ficticio al que llamó “la Isla de los Caballeros y los Knaves”. Los habitantes de la isla son o bien brillos, que siempre hacen declaraciones falsas, o caballeros, que siempre hacen declaraciones veraces.
En el más famoso rompecabezas de caballeros/puñaladas, estás en una habitación que solo tiene dos salidas. Uno lleva a la muerte segura y el otro a la libertad. Hay dos individuos en la habitación, y sabes que uno de ellos es caballero y el otro es un bridón, pero no sabes cuál. Tu reto es determinar la puerta que lleva a la libertad haciendo una sola pregunta.


