3.3: Pruebas indirectas- Contradicción y Contraposición
- Page ID
- 113984
Supongamos que estamos tratando de demostrar que todos los tordos son policíclicos 1. Una prueba directa de esto implicaría buscar la definición de lo que significa ser un tordo, y de lo que significa ser policíclico, y de alguna manera discernir una manera de convertir cualquier equivalente lógico del tordo en el equivalente lógico de policíclico. Como sucede con bastante frecuencia, puede que no haya una manera obvia de lograr esta tarea. La prueba indirecta toma un rumbo completamente diferente. Supongamos que tuvieras un tordo que no fuera policíclico, y además, demuestra que esta suposición lleva a algo verdaderamente imposible. Bueno, si es imposible que un tordo no sea policíclico, entonces debe darse el caso de que todos ellos lo sean. Tal argumento se conoce como prueba por contradicción.
Muy posiblemente la prueba indirecta más dulce conocida es la prueba de Euclides de que hay un número infinito de primos.
(Euclides) El conjunto de todos los números primos es infinito.
- Prueba
-
Supongamos por el contrario que sólo hay un número finito de primos. Este conjunto finito de números primos podría, en principio, ser listado en orden ascendente.
\ (\ {p_1, p_2, p_3,.., p_n\})
Considera el número\(N\) formado\(1\) al sumar al producto de todos estos primos.
\(N = 1 + \prod_{k=1}^{n} p_k \)
Claramente,\(N\) es mucho más grande que el prime más grande\(p_n\), por lo que\(N\) no puede ser un número primo en sí mismo. Por lo tanto,\(N\) debe ser producto de algunos de los primos de la lista. Supongamos que\(p_j\) es uno de los primos que divide\(N\). Ahora fíjense que, por construcción,\(N\) dejaría resto\(1\) tras división por\(p_j\). Esto es una contradicción ya que no podemos tener ambos\(p_j |N\) y\(p_j ∤ N\).
Dado que la suposición de que sólo hay finitamente muchos primos conduce a una contradicción, efectivamente debe haber un número infinito de primos.
Q.E.D.
Si estás trabajando en probar un SCP y el enfoque directo parece estar fallando puedes encontrar que otro enfoque indirecto, prueba por contraposición, hará el truco. En cierto sentido esta técnica de prueba no es realmente tan indirecta; lo que se hace es determinar el contrapositivo del condicional original y luego probarlo directamente. En otro sentido este método es indirecto porque una prueba por contraposición suele ser refundido como prueba por contradicción con bastante facilidad.
La prueba más fácil que conozco de usar el método de contraposición (y posiblemente el mejor ejemplo de esta técnica) es la prueba del lema que afirmamos en la Sección 1.6 en el curso de demostrar que no\(\sqrt{2}\) era racional. En caso de que lo hayas olvidado, necesitábamos el hecho de que siempre\(x^2\) es un número par, así es\(x\).
Primero expresemos esto como un UCS.
\(∀x ∈ \mathbb{Z}, x^2 \text{ even } \implies x \text{ even}\)
A lo mejor intentaste probar este resultado antes. Si es así probablemente te topaste con el problema conceptual con el que todo lo que tienes que trabajar es\(x^2\) cuya uniformidad no te da mucha munición al tratar de demostrar que\(x\) es parejo. El contrapositivo de esta afirmación es:
\(∀x ∈ \mathbb{Z}, x \text{ not even } \implies x^2 \text{ not even }\)
Ahora, ya que\(x\) y\(x^2\) son enteros, solo hay una alternativa a estar parejo — así podemos reexpresar lo contrapositivo como
\(∀x ∈ \mathbb{Z}, x \text{ odd } \implies x^2 \text{ odd }.\)
Sin más preámbulos, aquí está la prueba:
\[∀x ∈ \mathbb{Z}, x^2 \text{ even } \implies x \text{ even }\]
- Prueba
-
Esta afirmación es lógicamente equivalente a
\(∀x ∈ \mathbb{Z}, x \text{ odd } \implies x^2 \text{ odd }\)
así que lo demostramos en su lugar.
Supongamos que\(x\) es un entero particular pero arbitrariamente elegido tal que\(x\) es impar. Ya que\(x\) es impar, hay un entero\(k\) tal que\(x = 2k + 1\). De ello se deduce que\(x^2 = (2k + 1)^2 = 4k^2 + 4k + 1 = 2(2k^2 + 2k) + 1\). Por último, vemos que\(x^2\) debe ser impar porque es de la forma\(2m + 1\), donde\(m = 2k^2 + 2k\) es claramente un entero.
Q.E.D.
El principal problema al aplicar el método de prueba por contradicción es que generalmente implica “astucia”. Hay que llegar a alguna razón por la que la presunción de que el teorema es falso lleve a una contradicción —y esto puede o no ser obvio. Más que cualquier otra técnica de prueba, la prueba por contradicción exige que usemos borradores y reescritura. Después de monkear lo suficiente como para que encontremos la manera de llegar a una contradicción, tenemos que volver al inicio de la prueba y resaltar la característica que eventualmente contradiremos! Después de todo, queremos que parezca que nuestras pruebas son completamente claras, concisas y razonables incluso si su formulación nos causó algún tipo de angustia mental a nivel gordiano.
Terminaremos esta sección con un ejemplo de Geometría.
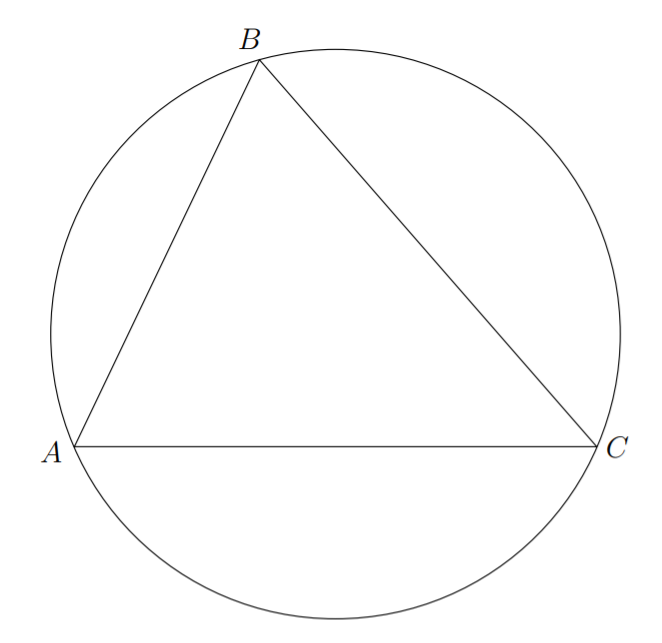
Entre todos los triángulos inscritos en un círculo fijo, el que tiene área máxima es equilátero.
- Prueba
-
Procederemos por contradicción. Supongamos al contrario que hay un triángulo,\(\triangle ABC\), inscrito en un círculo que tiene área máxima que no es equilátero. Ya que no\(\triangle ABC\) es equilátero, hay dos lados del mismo que no son iguales. Sin pérdida de generalidad, supongamos que los lados\(\overline{AB}\) y\(\overline{BC}\) tienen diferentes longitudes. Considera que el lado restante (\(\overline{AC}\)) es la base de este triángulo. Podemos construir otro triángulo\(\triangle AB'C\), también inscrito en nuestro círculo, y teniendo también\(\overline{AC}\) como base, teniendo una altitud mayor que\(\triangle ABC\) — ya que el área de un triángulo viene dada por la fórmula\(\dfrac{bh}{2}\) (dónde\(b\) está la base, y\(h\) es la altitud), este triángulo es área es evidentemente mayor que la de\(\triangle ABC\). Esto es una contradicción ya que\(\triangle ABC\) se presumió que tenía área máxima.
Dejamos la construcción real\(\triangle AB'C\) al siguiente ejercicio.
Q.E.D.
¿Dónde debemos colocar el punto\(B'\) para crear un triángulo\(\triangle AB'C \) que tenga mayor área que cualquier triángulo como el\(\triangle ABC \) que no sea isósceles?
Ejercicios:
Demostrar que si el cubo de un entero es impar, entonces ese entero es impar.
Demostrar que siempre que un primo\(p\) no divide el cuadrado de un entero, tampoco divide el entero original. \((p ∤ x^2 \implies p ∤ x)\)
Demostrar (por contradicción) que no hay un entero más grande.
Demostrar (por contradicción) que no existe el menor número real positivo.
Demostrar (por contradicción) que la suma de un número racional e irracional es irracional.
Demostrar (por contraposición) que para todos los enteros\(x\) y\(y\), si\(x + y\) es impar, entonces\(x \neq y\).
Demostrar (por contraposición) que para todos los números reales\(a\) y\(b\), si\(ab\) es irracional, entonces\(a\) es irracional o\(b\) es irracional.
Un triple pitagórico es un conjunto de tres números naturales,\(a\),\(b\) y\(c\), tal que\(a^2 + b^2 = c^2\). Demostrar que, en un triple pitagórico, al menos uno de\(a\) y\(b\) es parejo. Utilizar ya sea una prueba por contradicción o una prueba por contraposición.
Supongamos que tiene\(2\) pares de números reales positivos cuyos productos son\(1\). Es decir, tienes\((a, b)\) y\((c, d)\) en\(\mathbb{R}^2\) satisfacer\(ab = cd = 1\). Demostrar que a < c implica eso\(b > d\).


