3.5: Pruebas aún más directas, por casos y por agotamiento
- Page ID
- 113968
La prueba por agotamiento es el método de prueba menos atractivo desde una perspectiva estética. Una prueba exhaustiva consiste en verificar literal (y exhaustivamente) cada elemento del universo para ver si la afirmación dada es cierta para ello. Por lo general, por supuesto, esto es imposible porque el universo del discurso es infinito; pero cuando el universo del discurso es finito, ciertamente no se puede argumentar la validez de una prueba exhaustiva.
En las últimas décadas, la introducción de una poderosa asistencia computacional para matemáticos ha llevado a una situación divertida. Existe una lista creciente de resultados importantes que han sido “probados” por el agotamiento usando una computadora. Ejemplos importantes de este fenómeno son la inexistencia de un plano de orden proyectivo\(10\) [10] y el único valor conocido de un número Ramsey para los hipergrafos [13].
Prueba por casos es sutilmente diferente de la prueba exhaustiva; por un lado, una prueba válida por casos puede ser utilizada en un universo infinito. En una prueba por casos, uno tiene que dividir el universo del discurso en un número finito de conjuntos 1 y luego proporcionar una prueba separada para cada uno de los casos. Un gran número de declaraciones sobre los enteros se pueden probar usando la división de enteros en pares e impares. Otro conjunto de casos que se utiliza frecuentemente es el número finito de posibles restos obtenidos al dividir por un entero\(d\). (Obsérvese que par e impar corresponden a los restos\(0\) y\(1\) se obtienen después de la división por\(2\).)
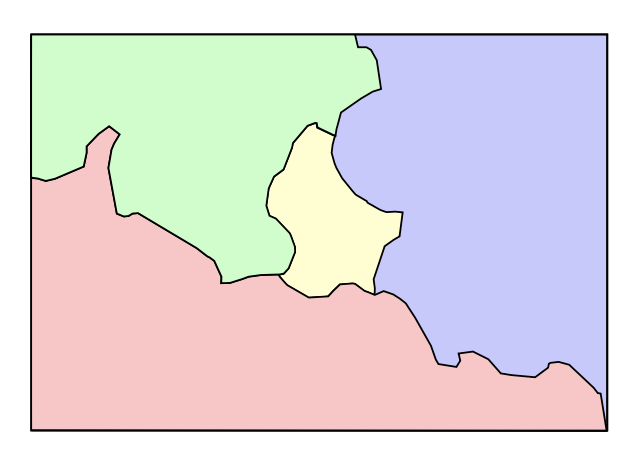
Una instancia muy famosa de prueba por casos es la prueba asistida por computadora del teorema de cuatro colores. El teorema de cuatro colores es un resultado conocido por los creadores de mapas desde hace bastante tiempo que dice que\(4\) los colores siempre son suficientes para colorear a las naciones en un mapa de tal manera que los países que comparten un límite siempre se colorean de manera diferente. La figura\(3.5.1\) muestra una instancia de un arreglo de naciones que requiere al menos cuatro colores diferentes, el teorema dice que cuatro colores siempre son suficientes. Cabe señalar que los cartógrafos reales suelen reservar un quinto color para los océanos (y otras aguas) y que es posible concebir un mapa que requiera cinco colores si uno permite que las naciones sean no contiguas. En\(1977\), Kenneth Appel y Wolfgang Haken probaron el teorema de cuatro colores al reducir la infinitud de posibilidades para\(1,936\) separar casos y analizar cada uno de estos con una computadora. La inelegancia de una prueba por casos es probablemente proporcional a alguna potencia del número de casos, pero en todo caso, esta prueba generalmente se considera algo poco elegante. Desde que se anunció la prueba ha habido un esfuerzo continuo para reducir el número de casos (actualmente el registro son\(633\) casos —todavía demasiados para ser revisados sin computadora) o para encontrar una prueba que no se base en los casos. Para un buen artículo introductorio sobre el teorema de cuatro colores ver [6].
Las pruebas más exhaustivas de declaraciones que no son triviales tienden a ser (literalmente) demasiado agotadoras o a parecer más bien ideadas. Un ejemplo de una situación en la que existe una prueba exhaustiva de alguna afirmación es cuando se piensa que la declaración es universalmente cierta pero no se conoce ninguna prueba general —sin embargo, la declaración ha sido verificada para un gran número de casos. La conjetura de Goldbach es una de esas afirmaciones. Christian Goldbach [4] fue un matemático nacido en Königsberg Prusia, quien, curiosamente, no hizo la conjetura 2. que lleva su nombre. En una carta a Leonard Euler, Goldbach conjeturó que cada número impar mayor que\(5\) podría expresarse como la suma de tres primos (hoy en día esto se conoce como la débil conjetura de Goldbach). Al parecer, a Euler le gustó el problema y respondió a Goldbach afirmando lo que ahora se conoce como la conjetura de Goldbach: Cada número par mayor que se\(2\) puede expresar como la suma de dos primos. Esta declaración ha estado por ahí desde entonces\(1742\), y muchos de los mejores matemáticos del mundo han hecho sus intentos de demostrarlo, ¡en ningún resultado! (Bueno, en realidad se ha avanzado mucho pero el resultado aún no se ha probado). Es fácil verificar la conjetura de Goldbach para números pares relativamente pequeños, así que lo que se ha hecho es/son pruebas por agotamiento de la conjetura de Goldbach restringidas a universos finitos. A partir de este escrito, se ha verificado que la conjetura es cierta de todos los números pares menores que\(2 × 10^{17}\).
Siempre que exista una prueba exhaustiva, o una prueba por casos para alguna afirmación, generalmente se considera que una prueba directa sería más estéticamente agradable. Si se encuentra en una situación que no admite tal prueba directa, al menos debe buscar una prueba por casos utilizando el mínimo número posible de casos. Por ejemplo, considere el siguiente teorema y prueba.
\(∀n ∈ \mathbb{Z} n^2\)es de la forma\(4k\) o\(4k + 1\) para algunos\(k ∈ \mathbb{Z}\).
- Prueba
-
Consideraremos los cuatro casos determinados por los cuatro posibles residuos\(\text{mod } 4\).
caso i) Si\(n ≡ 0\)\((\text{mod } 4)\) entonces hay un entero\(m\) tal que\(n = 4m\). De ello se deduce que\(n^2 = (4m)^2 = 16m^2\) es de la forma\(4k\) donde\(k\) está\(4m^2\).
caso ii) Si\(n ≡ 1\)\((\text{mod } 4)\) entonces hay un entero\(m\) tal que\(n = 4m + 1\). De ello se deduce que\(n^2 = (4m + 1)^2 = 16m^2 + 8m + 1\) es de la forma\(4k + 1\) donde k está\(4m^2 + 2m\).
caso iii) Si\(n ≡ 2\)\((\text{mod } 4)\) entonces hay un entero\(m\) tal que\(n = 4m + 2\). De ello se deduce que\(n^2 = (4m + 2)^2 = 16m^2 + 16m + 4\) es de la forma\(4k\) donde\(k\) está\(4m^2 + 4m + 1\).
caso iv) Si\(n ≡ 3\)\((\text{mod } 4)\) entonces hay un entero\(m\) tal que\(n = 4m + 3\). De ello se deduce que\(n^2 = (4m + 3)^2 = 16m^2 + 24m + 9\) es de la forma\(4k + 1\) donde\(k\) está\(4m^2 + 6m + 2\).
Dado que estos cuatro casos agotan las posibilidades y dado que el resultado deseado se mantiene en cada caso, nuestra prueba está completa.
Q.E.D.
Si bien la prueba que acabamos de exponer es ciertamente válida, el argumento es poco elegante ya que bastaría con un número menor de casos.
El teorema anterior se puede probar usando solo dos casos. Hazlo.
Cerraremos esta sección pidiéndole que determine una prueba exhaustiva donde la complejidad del argumento es desafiante pero no demasiado imposible.
Graph guijarros es un concepto interesante originado por el famoso combinatorialista Fan Chung. Un “grafo” (como se usa aquí el término) es una colección de lugares o ubicaciones que se conocen como “nodos”, algunos de los cuales están unidos por caminos o conexiones que se conocen como “bordes”. Las gráficas han sido estudiadas por matemáticos\(400\) desde hace unos años., y se pueden poner muchos problemas interesantes en este entorno. El guijarros de gráficos es una versión cruda de un problema más amplio en la gestión de recursos, a menudo un recurso realmente se usa en el proceso de transportarlo. Piense en los grandes camiones cisterna que se utilizan para transportar gasolina. ¿En qué se ejecutan? Bueno, en realidad probablemente quemen diesel —pero el punto es que para mover el combustible hay que consumir algo de él. Graph guijarros lleva esto a un extremo: para mover un guijarro debemos consumir un guijarro.
Imagínese que un montón de guijarros se distribuyen aleatoriamente en los nodos de una gráfica, y que se nos permite hacer movimientos de guijarros gráficos — eliminamos dos guijarros de algún nodo y colocamos un solo guijarro en un nodo que está conectado a él. Ver Figura\(3.5.3\).
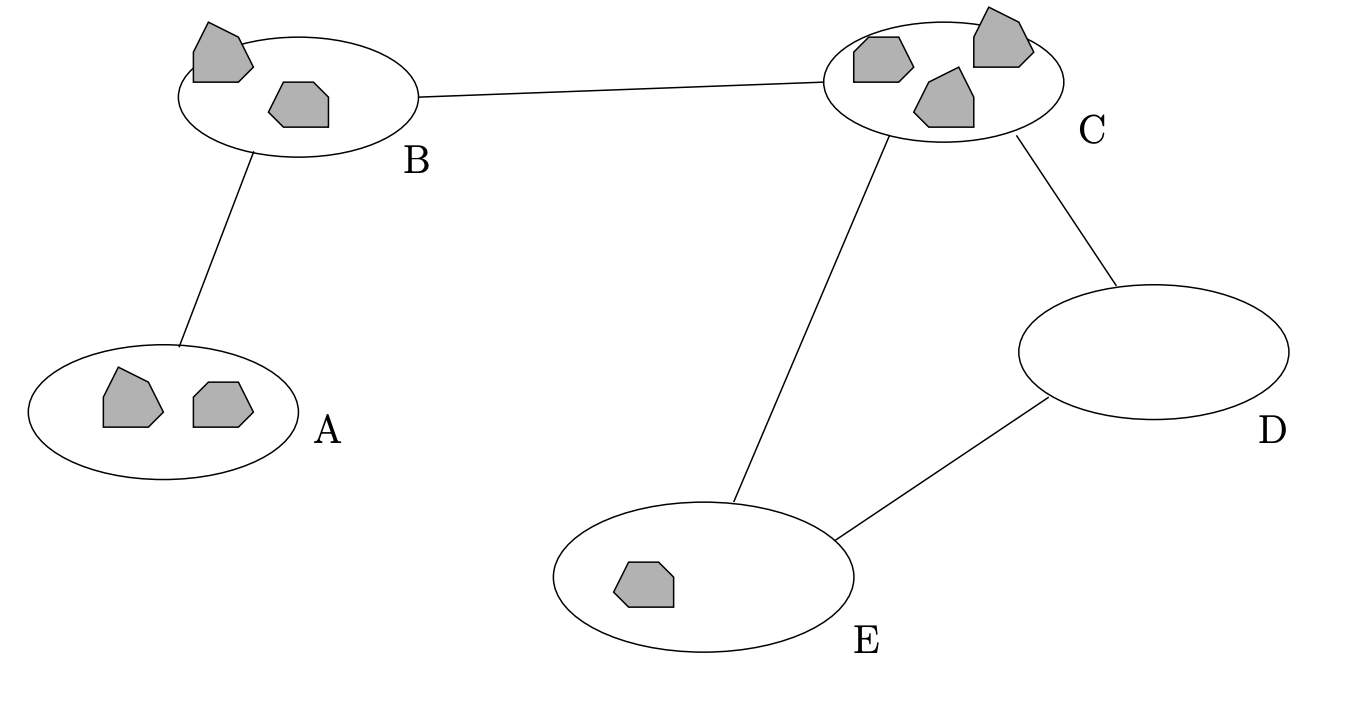
Para cualquier gráfica en particular, podemos pedir su número de guijeado,\(ρ\). Este es el número más pequeño de manera que si los guijarros de ρ se distribuyen de alguna manera en los nodos de la gráfica, será posible usar movimientos de guijarros para obtener un guijarro a cualquier nodo.
Por ejemplo, considere la gráfica triangular, tres nodos que están todos conectados entre sí. El número de guijados de esta gráfica es\(3\). Si empezamos con un guijarro en cada nodo ya estamos terminados; si hay un nodo que tiene dos guijarros en él, podemos usar un movimiento de guijarros para llegar a cualquiera de los otros dos nodos.
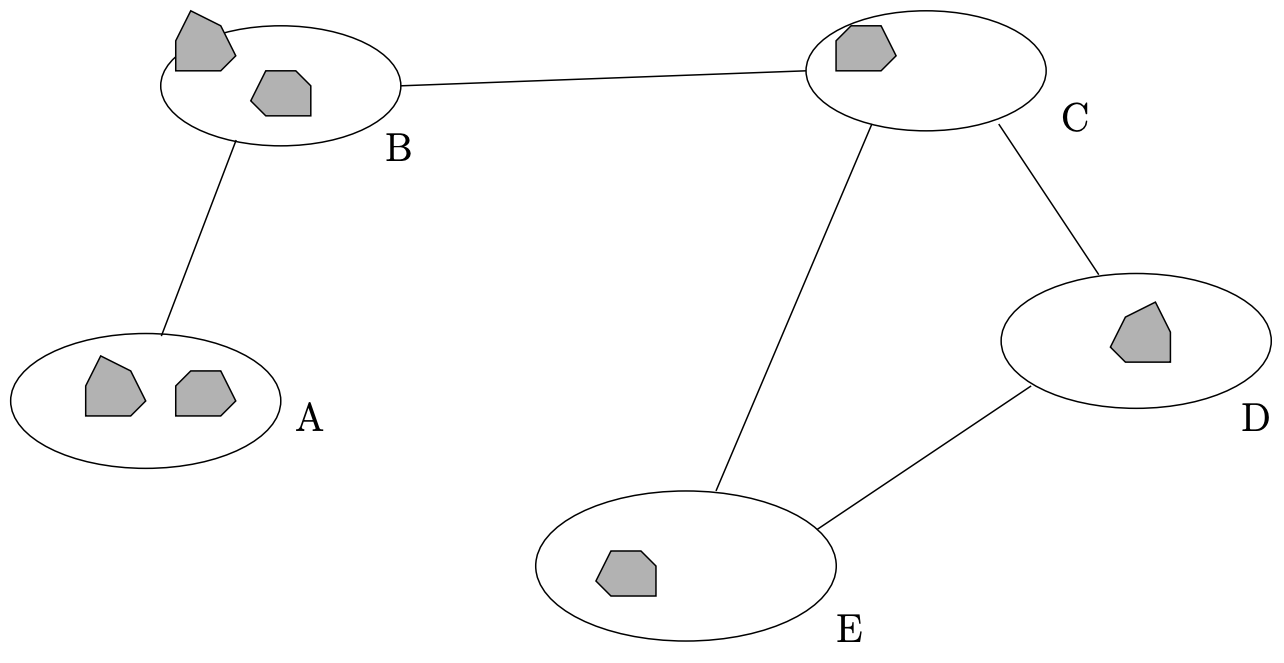
Hay una gráfica\(C_5\) que consiste en\(5\) nodos conectados de manera circular. Determinar su número de guijados. Demuestra tu respuesta exhaustivamente.
Pista: el número de guijarros debe ser mayor que\(4\) porque si se coloca un guijarro en cada uno de\(4\) los nodos la configuración es inamovible (necesitamos tener dos guijarros en un nodo para poder hacer un movimiento de guijarros en absoluto) y así nunca se puede llegar al\(5^{\text{th}}\) nodo.
Ejercicios:
Demostrar que si\(n\) es un número impar entonces\(n^4 (\text{mod } 16) = 1\).
Demostrar que cada número primo que no sea\(2\) y\(3\) tiene la forma\(6q + 1\) o\(6q + 5\) para algún número entero\(q\).
- Pista
-
Este problema implica pensar tanto en casos como en contrapositivos.
Mostrar que la suma de tres enteros consecutivos cualquiera es divisible por\(3\).
Hay una gráfica conocida como\(K_4\) que tiene\(4\) nodos y hay un borde entre cada par de nodos. El número de guijarros de\(K_4\) tiene que ser al menos\(4\) ya que sería posible poner un guijarro en cada uno de\(3\) los nodos y no poder llegar al nodo restante usando movimientos de guijarros. Demuestre que el número de guijados de\(K_4\) es en realidad\(4\).
Encuentra el número de guijarros de una gráfica cuyos nodos son las esquinas y cuyos bordes son los, uhmm, bordes de un cubo.
Un número vampiro es un número de\(2n\) dígito\(v\) que factores como\(v = xy\) dónde\(x\) y\(y\) son\(n\) números de dígitos y los dígitos de\(v\) son precisamente los dígitos en\(x\) y\(y\) en algún orden. Los números\(x\) y\(y\) se conocen como los “colmillos” de\(v\). Para eliminar casos triviales, ambos colmillos no pueden terminar con\(0\).
Demuestre que no hay números de vampiros\(2\) -dígitos.
Demuestre que hay números de vampiros de\(4\) siete dígitos
El teorema de Lagrange sobre la representación de números enteros como sumas de cuadrados dice que cada entero positivo se puede expresar como la suma de a lo sumo\(4\) cuadrados. Por ejemplo,\(79 = 7^2 + 5^2 + 2^2 + 1^2\). Mostrar (exhaustivamente) que no se\(15\) puede representar usando menos de\(4\) cuadrados.
Demuestre que hay exactamente\(15\) números\(x\) en el rango\(1 ≤ x ≤ 100\) que no se pueden representar usando menos de\(4\) cuadrados.
La propiedad de tricotomía de los números reales simplemente establece que cada número real es positivo o negativo o cero. La tricotomía puede ser utilizada para probar muchas afirmaciones al observar los tres casos que garantiza. Desarrollar una prueba (por casos) de que el cuadrado de cualquier número real no es negativo.
Consideremos el juego llamado “determinante binario tic-tac-toe” 3 el cual es jugado por dos jugadores que alternativamente rellenan las entradas de una\(3 × 3\) matriz. El Jugador Uno va primero, colocándose\(1\) en la matriz y el jugador Cero va segundo,\(0\) colocando's El objetivo del Jugador Uno es que la matriz final tenga determinante\(1\), y el objetivo del jugador Zero es que el determinante sea\(0\). Se llevan a cabo los cálculos determinantes\(\text{mod } 2\).
Demuestre que el jugador Zero siempre puede ganar un juego de tic-tac-toe determinante binario por el método del agotamiento.