3.6: Pruebas y despruebas de declaraciones existenciales
- Page ID
- 113983
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Desde cierto punto de vista, no hay necesidad de la sección actual. Si estamos demostrando una afirmación existencial estamos desmentiendo alguna afirmación universal. (Que ya se discutió.) Del mismo modo, si estamos tratando de desmentir una afirmación existencial, entonces en realidad estamos demostrando una declaración universal relacionada. Sin embargo, a veces la forma en que se afirma un teorema enfatiza la cuestión de existencia sobre el universal correspondiente, y así la gente habla de probar y desmentir las afirmaciones existenciales como un tema separado de los enunciados universales.
Las pruebas de preguntas existenciales vienen en dos variedades básicas: constructivas y no constructivas. Las pruebas constructivas son conceptualmente las más fáciles de las dos; en realidad se nombra un ejemplo que demuestre que la cuestión existencial es verdadera. Por ejemplo:
Hay un primo par.
- Prueba
-
El número\(2\) es a la vez par y primo.
Q.E.D.
Los números de Fibonacci se definen por los valores iniciales\(F(0) = 1\)\(F(1) = 1\) y y la fórmula recursiva\(F(n + 1) = F(n) + F(n − 1)\) (para obtener el siguiente número de la serie se agrega el último y el penúltimo).
| \(n\) | \(F(n)\) |
|---|---|
| \ (n\) ">\(0\) | \ (F (n)\) ">\(1\) |
| \ (n\) ">\(1\) | \ (F (n)\) ">\(1\) |
| \ (n\) ">\(2\) | \ (F (n)\) ">\(2\) |
| \ (n\) ">\(3\) | \ (F (n)\) ">\(3\) |
| \ (n\) ">\(4\) | \ (F (n)\) ">\(5\) |
| \ (n\) ">\(5\) | \ (F (n)\) ">\(8\) |
| \ (n\) ">\(⋮\) | \ (F (n)\) ">\(⋮\) |
Demostrar que hay un número de Fibonacci que es un cuadrado perfecto.
Una prueba de existencia no constructiva es más problemática. Un enfoque es argumentar por contradicción —si lo que buscamos no existe eso conducirá a un absurdo. Otro enfoque es delinear un algoritmo de búsqueda para el elemento deseado y proporcionar un argumento de por qué no puede fallar!
Un enfoque particularmente limpio es argumentar usando dilema. Este es mi teoreo/prueba existencial no constructivo favorito.
Hay números irracionales\(α\) y\(β\) tal eso\(α^β\) es racional.
- Prueba
-
Si\(\sqrt{2}^{\sqrt{2}}\) es racional entonces estamos hechos. (Vamos\(α = β = \sqrt{2}\).) De lo contrario, vamos\(α = \sqrt{2}^{\sqrt{2}}\) y\(β = \sqrt{2}\). El resultado sigue porque\(\left( \sqrt{2}^{\sqrt{2}} \right)^{\sqrt{2}} = \sqrt{2}^{(\sqrt{2}\sqrt{2})} = \sqrt{2}^{2} = 2\), que es claramente racional.
Q.E.D.
Muchas pruebas existenciales involucran una propiedad de los números naturales conocida como el principio bien ordenado. El principio bien ordenado a veces se abrevia WOP. Si un conjunto tiene WOP no significa que el conjunto esté ordenado de una manera particularmente buena, sino que sus subconjuntos son como pozos, del tipo que saca agua con un cubo en una cuerda. No necesita preocuparse por WOP en general en este punto, pero observe que los subconjuntos de los números naturales tienen una propiedad particularmente agradable: cualquier conjunto no vacío de números naturales debe tener un elemento mínimo (al igual que cada pozo de agua tiene un fondo).
Debido a que los números naturales tienen el principio bien ordenado podemos probar que hay un número menos natural con propiedad simplemente\(\text{X}\) encontrando cualquier número natural con propiedad\(\text{X}\) — al hacer eso hemos demostrado que el conjunto de números naturales con propiedad no\(\text{X}\) está vacío y esa es la única hipótesis que necesita el WOP.
Por ejemplo, en los ejercicios de la Sección 3.5 introdujimos los números de vampiros. Un número vampiro es un número de\(2n\) dígito\(v\) que factores como\(v = xy\) dónde\(x\) y\(y\) son\(n\) números de dígitos y los dígitos de\(v\) son precisamente los dígitos en\(x\) y\(y\) en algún orden. Los números\(x\) y\(y\) se conocen como los “colmillos” de\(v\). Para eliminar casos triviales, ambos colmillos pueden no terminar con ceros.
Hay un número de vampiro\(6\) de menor dígito.
- Prueba
-
El número\(125460\) es un número vampiro (de hecho este es el ejemplo más pequeño de un número de vampiro con dos juegos de colmillos:\(125460 = 204 · 615 = 246 · 510\)). Dado que el conjunto\(6\) de números de vampiros de dígitos no está vacío, el principio bien ordenado de los números naturales nos permite deducir que hay un número de vampiro\(6\) de menor dígito.
Q.E.D.
Esta es una situación bastante interesante ya que sabemos que hay un número de vampiro\(6\) de menor dígito sin tener idea de lo que es!
Demuestre que\(102510\) es el número\(6\) de vampiro más pequeño de dígitos.
Hay bastantes ocasiones en las que necesitamos probar declaraciones que involucren al cuantificador de existencia único\((∃!)\). En tales casos, necesitamos hacer solo un poco más de trabajo. Tenemos que mostrar la existencia —ya sea constructiva o no constructivamente— y también necesitamos mostrar singularidad. Para dar un ejemplo de una prueba de existencia única, volveremos a un concepto que se discutió primero en la Sección 1.5 y terminaremos algunos negocios que se pasaron por alto allí.
Recordemos el algoritmo euclidiano que se utilizó para calcular el mayor divisor común de dos enteros\(a\) y\(b\) (que denotamos\(\text{gcd}(a, b)\)). Hay una pregunta bastante importante sobre los algoritmos conocidos como el “problema de la detención”. ¿El programa finalmente se detiene o se atasca en un bucle infinito? Sabemos que el algoritmo euclidiano se detiene (y genera el resultado correcto) porque conocemos el siguiente resultado de existencia único.
\(∀a, b ∈ \mathbb{Z} +, ∃! d ∈ \mathbb{Z}^+\)de tal manera que\(d = \text{gcd}(a, b)\)
Ahora, antes de que podamos probar este resultado, necesitaremos una definición precisa para\(\text{gcd}(a, b)\). En primer lugar, a\(\text{gcd}\) debe ser un divisor común lo que significa que necesita dividir ambos\(a\) y\(b\). En segundo lugar, entre todos los divisores comunes, debe ser el más grande. Este segundo punto generalmente se aborda exigiendo que cada otro divisor común divida el\(\text{gcd}\). Por último, hay que señalar que a siempre\(\text{gcd}\) es positivo, porque siempre que un número divide otro número también lo hace su negativo, ¡y cualquiera de esos dos que sea positivo será claramente el mayor! Esto nos permite extender la definición de\(\text{gcd}\) a todos los enteros, pero las cosas son conceptualmente más fáciles si mantenemos nuestra atención restringida a los enteros positivos.
El mayor divisor común, o gcd, de dos enteros positivos\(a\) y\(b\) es un entero positivo\(d\) tal que\(d | a\) y\(d | b\) y si\(c\) es cualquier otro entero positivo tal que\(c |a\) y\(c | b\) entonces\(c |d\).
\[∀a, b, c, d ∈ \mathbb{Z}^+ d = \text{gcd}(a, b) \iff d|a ∧ d| b ∧ (c |a ∧ c | b \implies c |d)\]
Armados con esta definición, volvamos nuestra atención a probar la existencia única del\(\text{gcd}\). La parte de la singularidad es más fácil así que lo haremos primero. Argumentamos por contradicción. Supongamos que hubo dos números diferentes\(d\) y\(d'\) satisfaciendo la definición de\(\text{gcd}(a, b)\). Poner\(d'\) en el lugar de\(c\) en la definición para ver eso\(d' | d\). De igual manera, podemos deducir eso\(d | d'\) y si dos números cada uno se dividen en el otro, deben ser iguales. Esto es una contradicción ya que asumimos\(d\) y\(d'\) fuimos diferentes.
Para la parte de existencia, necesitaremos definir un conjunto —conocido como el\(\mathbb{Z}\) -módulo generado por\(a\) y\(b\) — que consiste en todos los números de la forma\(xa+yb\) donde\(x\) y\(y\) rango sobre los enteros.
Este conjunto tiene un carácter geométrico muy bonito que muchas veces no recibe la atención que merece. Cada elemento de un\(\mathbb{Z}\) -módulo generado por dos números (\(15\)y\(21\) en el ejemplo) corresponde a un punto en el plano euclidiano. Como se indica en la Figura\(3.6.1\) hay una línea divisoria entre los elementos positivos y negativos en un\(\mathbb{Z}\) módulo. También es fácil ver que hay muchas repeticiones del mismo valor en diferentes puntos del plano.
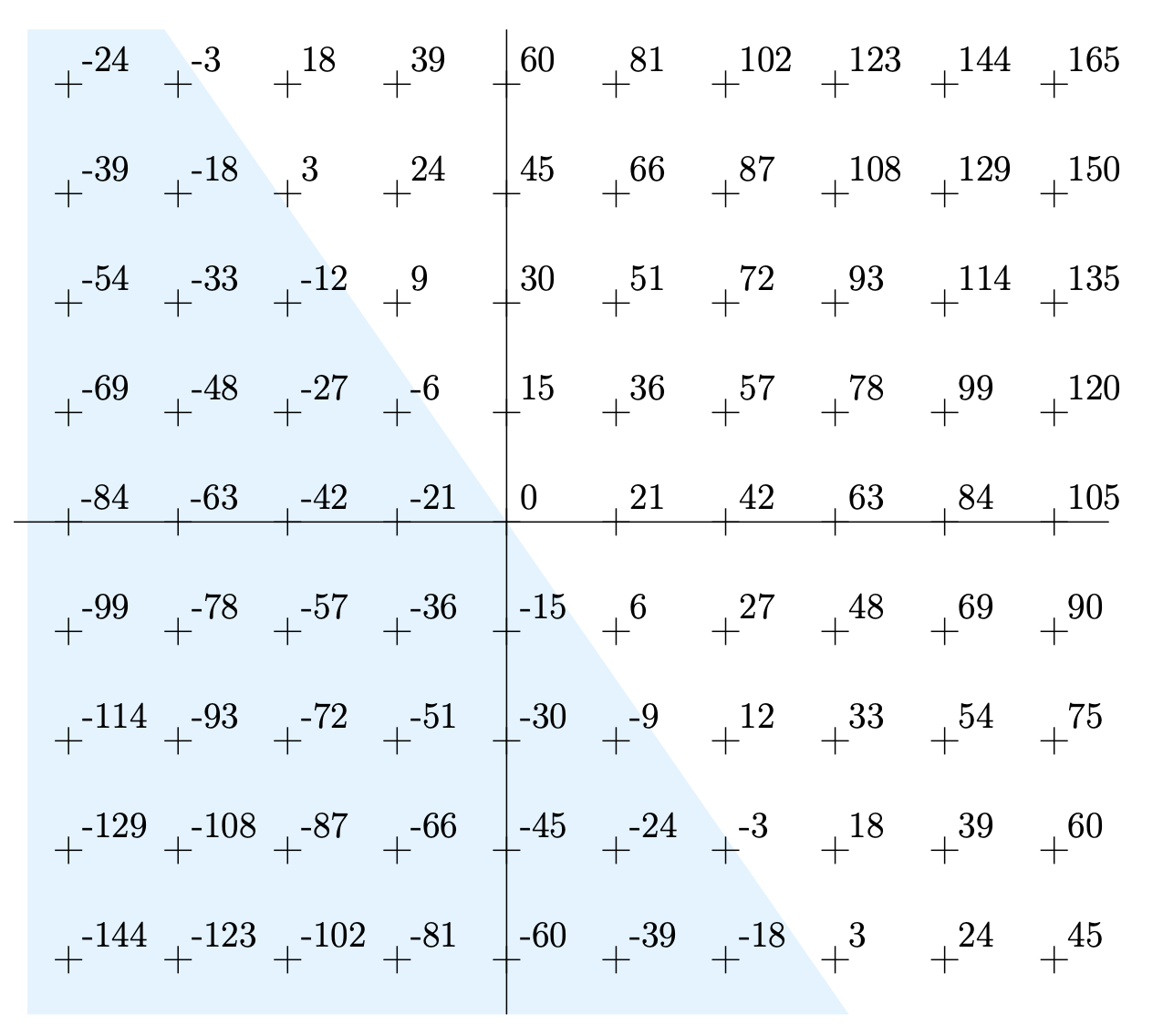
El valor se produce\(0\) claramente en un\(\mathbb{Z}\) -módulo cuando ambos\(x\) y ellos mismos\(y\) son cero. Encuentra otro par de\((x, y)\) valores tal que\(21x + 15y\) sea cero. ¿Cuál es la pendiente de la línea que separa los valores positivos de los negativos en nuestro\(\mathbb{Z}\) -módulo?
Al pensar en este\(\mathbb{Z}\) -módulo, y examinando Figura\(3.6.1\), es posible que haya notado que el número positivo más pequeño en el\(\mathbb{Z}\) módulo -es\(3\). Si no te habías dado cuenta de eso, mira hacia atrás y verifica ese hecho ahora.
¿Cómo sabemos que algún valor positivo menor (a\(1\) o a\(2\)) no ocurre en algún lugar del plano euclidiano?
Lo que acabamos de observar es una instancia particular de un resultado general.
El número positivo más pequeño en el\(\mathbb{Z}\) módulo -generado por\(a\) y\(b\) es\(d = \text{gcd}(a, b)\).
- Prueba
-
Supongamos que d es el número positivo más pequeño en el Zmodule\(\{xa+yb x, y ∈ \mathbb{Z}\}\). Hay valores particulares de\(x\) y\(y\) (que distinguiremos con overlines) tales que\(d = xa + yb\). Ahora bien, es fácil ver que si\(c\) hay algún divisor común de\(a\) y\(b\) luego\(c |d\), entonces lo que queda por probar es que\(d\) en sí mismo es un divisor de ambos\(a\) y\(b\). Considera\(d\) dividir en\(a\). Por el algoritmo de división, hay números determinados de manera única\(q\) y\(r\) tal que\(a = qd+r\) con\(0 ≤ r < d\). Demostraremos que\(r = 0.\) Supongamos, al contrario, que r es positivo. Tenga en cuenta que podemos escribir\(r\) como\(r = a − qd = a − q(\overline{x}a + \overline{y}b) = (1 − q \overline{x})a − q \overline{y}b\). La última igualdad muestra que\(r\) está en el\(\mathbb{Z}\) -módulo bajo consideración, y así, dado que\(d\) es el entero positivo más pequeño en este\(\mathbb{Z}\) -módulo se deduce aquello\(r ≥ d\) que contradice el hecho anteriormente señalado que\(r < d\). Así,\(r = 0\) y así se deduce que\(d | a\). Un argumento enteramente análogo puede ser utilizado para mostrar aquello\(d| b\) que completa la prueba de que\(d = \text{gcd}(a, b)\).
Q.E.D.
Ejercicios:
Demostrar que hay un cuadrado perfecto que es la suma de dos cuadrados perfectos.
Demuestre que hay un cubo perfecto que es la suma de tres cubos perfectos.
Demuestre que el WOP no se sostiene en los enteros. (Esta es una prueba de existencia, demuestras que hay un subconjunto de\(\mathbb{Z}\) que no tiene un elemento más pequeño).
Demuestre que el WOP no aguanta\(\mathbb{Q}^+\).
En la prueba del Teorema\(3.6.3\) nos comadreñamos de mostrar eso\(d | b\). Rellene esa parte del comprobante.
Dar una prueba de la existencia única de\(q\) y\(r\) en el algoritmo de división.
Un dígrafo es un dibujo que contiene una colección de puntos que están conectados por flechas. El juego conocido como tijeras-papel-rock puede ser representado por un dígrafo que está equilibrado (cada punto tiene el mismo número de flechas que salen que entran). Demostrar que hay un dígrafo equilibrado que tiene\(5\) puntos.