4.3: Operaciones de conjunto
- Page ID
- 114126
En esta sección, continuaremos desarrollando la correspondencia entre la Lógica y la Teoría de Conjuntos.
Los conectores lógicos\(∧\) y\(∨\) corresponden a las nociones teóricas de conjunto de unión\((∪)\) e intersección\((∩)\). Los símbolos están diseñados para proporcionar un mnemotécnico para la correspondencia; los símbolos de la teoría de conjuntos son solo versiones redondeadas de los de Logic.
De manera explícita, si\(P(x)\) y\(Q(x)\) son oraciones abiertas, entonces la unión de la verdad correspondiente establece\(S_P\) y\(S_Q\) se define por
\[S_P ∪ S_Q = \{x ∈ U P(x) ∨ Q(x)\}.\]
Supongamos que dos conjuntos\(A\) y\(B\) se dan. Reexpresar la definición anterior de “sindicato” utilizando sus criterios de afiliación,\(M_A(x) = “x ∈ A”\) y\(M_B(x) = “x ∈ B.”\)
La unión de más de dos conjuntos se puede expresar usando un símbolo de unión grande. Por ejemplo, consideremos la familia de intervalos reales definidos por\(I_n = (n, n + 1]\). 1 Hay un intervalo para cada entero\(n\). Además, cada número real está en uno de estos intervalos. La oración anterior puede expresarse como
\[\mathbb{R} = \bigcup_{n∈\mathbb{Z}} I_n.\]
La intersección de dos conjuntos se conceptualiza como “lo que tienen en común” pero la definición precisa se encuentra considerando conjunciones,
\[A ∩ B = \{x ∈ U x ∈ A ∧ x ∈ B\}.\]
Con referencia a dos oraciones abiertas\(P(x)\) y\(Q(x)\), definir la intersección de sus conjuntos de verdad,\(S_P ∩ S_Q\).
También hay una versión “grande” del símbolo de intersección. Usando la misma familia de intervalos que antes,
\[∅ = \bigcap_{n∈\mathbb{Z}} I_n. \]
Por supuesto, la intersección de cualquier par distinto de estos intervalos está vacía por lo que la declaración anterior no es particularmente fuerte.
La negación en la lógica corresponde a la complementación en la teoría de conjuntos. El complemento de un conjunto\(A\) suele ser denotado por\(\overline{A}\) (aunque algunos prefieren un superíndice\(c\) —como en\(A^c\)), este es el conjunto de todas las cosas que no están en\(A\). Al pensar en la complementación se ve rápidamente por qué se enfatiza la importancia de trabajar dentro de un conjunto universal bien definido. Considera el conjunto de todos los libros de texto de matemáticas. Obviamente, el complemento de este conjunto contendría textos en inglés, Ingeniería y Evolución —pero esa afirmación está asumiendo implícitamente que el universo del discurso es “libros de texto”. Es igualmente válido decir que una secuencia muy larga de ceros y unos, una fresa roja, y el número no\(\sqrt{\pi}\) son libros de texto de matemáticas y así estas cosas son todos elementos del complemento del conjunto de todos los libros de texto de matemáticas. Lo que realmente nos preocupa es el tema de si el complemento de un conjunto está bien definido o no, es decir, podemos decir con certeza si un ítem dado está o no en el complemento de un conjunto. Esta pregunta es decidible exactamente cuando la pregunta de membresía para el conjunto original es decidible. Mucha gente piensa que la razón principal para trabajar dentro de un conjunto universal fijo es que entonces tenemos complementos bien definidos. La verdadera razón por la que aceptamos esta restricción es para asegurar que tanto los criterios de membresía,\(M_A(x)\) como\(M_{\overline{A}}(x)\), sean sentencias abiertas decidibles. Como ejemplo del tipo de extrañeza que puede surgir, considere que durante el tiempo que yo, como autor de este libro, estaba escribiendo el último párrafo, este texto no era más que una secuencia muy larga de ceros y unos en la memoria de mi computadora.
Cada regla que aprendimos en el Capítulo 2 (ver Tabla\(2.3.1\)) tiene un equivalente teórico de conjunto. Estas versiones teóricas de conjuntos se expresan usando igualdades (es decir, el símbolo entre dos conjuntos) lo que\(=\) en realidad es un poco divertido si lo piensas bien. Normalmente usamos = para significar que dos números o variables tienen la misma magnitud numérica, como en\(12^2 = 144\), estamos haciendo algo completamente diferente cuando usamos ese símbolo entre dos conjuntos, como en\(\{1, 2, 3\} = \{ \sqrt{1}, \sqrt{4}, \sqrt{9}\}\), pero la gente parece estar acostumbrada a esto así que no tiene sentido cuestionar.
Desarrollar una definición útil para establecer la igualdad. En otras palabras, llegar a una declaración lógica (cuantificada) que signifique lo mismo que “\(A = B\)” para dos conjuntos arbitrarios\(A\) y\(B\).
¿Qué símbolo en Lógica debe ir entre los criterios de membresía\(M_A(x)\) y\(M_B(x)\) si\(A\) y\(B\) son conjuntos iguales?
En\(4.3.1\) la Tabla se recogen las reglas que rigen las interacciones entre las operaciones teóricas del conjunto.
Ahora estamos en una posición algo similar a cuando saltamos de probar afirmaciones lógicas con tablas de verdad a hacer pruebas de dos columnas. Tenemos dos enfoques diferentes para demostrar que dos conjuntos son iguales. Podemos hacer una prueba llamada “persiguiendo elementos” (para mostrar\(A = B\), asumir\(x ∈ A\) y probar\(x ∈ B\) y luego viceversa). O bien, podemos construir una prueba usando las igualdades de conjunto básicas dadas en la Tabla\(4.3.1\). A menudo, este último puede tomar la forma de una prueba de dos columnas.
| Tabla\(4.3.1\): Igualdades Teóricas de Conjuntos Básicos | ||
|---|---|---|
| \(\cap\) | \(\cup\) | |
| \ (4.3.1\): Igualdades teóricas de conjuntos básicos">Leyes conmutativas | \ (4.3.1\): Igualdades teóricas de conjuntos básicos\(\cap\) “>\(A \cap B = B \cap A\) | \ (4.3.1\): Igualdades teóricas de conjuntos básicos\(\cup\) “>\(A \cup B = B \cup A\) |
| \ (4.3.1\): Igualdades teóricas de conjuntos básicos">Leyes asociativas | \ (4.3.1\): Igualdades teóricas de conjuntos básicos\(\cap\) “>\(A \cap (B \cap C) = (A \cap B) \cap C\) | \ (4.3.1\): Igualdades teóricas de conjuntos básicos\(\cup\) “>\(A \cup (B \cup C)= (A \cup B) \cup C\) |
| \ (4.3.1\): Igualdades teóricas de conjuntos básicos">Leyes distributivas | \ (4.3.1\): Igualdades teóricas de conjuntos básicos\(\cap\) “>\(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\) | \ (4.3.1\): Igualdades teóricas de conjuntos básicos\(\cup\) “>\(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\) |
| \ (4.3.1\): Igualdades teóricas de conjuntos básicos">Leyes de Demorgan | \ (4.3.1\): Igualdades teóricas de conjuntos básicos\(\cap\) “>\(\overline{A \cap B} = \overline{A} \cup \overline{B}\) | \ (4.3.1\): Igualdades teóricas de conjuntos básicos\(\cup\) “>\(\overline{A \cup B} = \overline{A} \cap \overline{B}\) |
| \ (4.3.1\): Igualdades teóricas de conjuntos básicos">Complemento doble | \ (4.3.1\): Igualdades teóricas de conjuntos básicos\(\cap\) “>\(\overline{\overline{A}} = A\) | \ (4.3.1\): Igualdades teóricas de conjuntos básicos\(\cup\) “>\(\text{same}\) |
| \ (4.3.1\): Igualdades teóricas de conjuntos básicos">Complementariedad | \ (4.3.1\): Igualdades teóricas de conjuntos básicos\(\cap\) “>\(A \cap \overline{A} = ∅\) | \ (4.3.1\): Igualdades teóricas de conjuntos básicos\(\cup\) “>\(A \cup \overline{A} = U\) |
| \ (4.3.1\): Igualdades teóricas de conjuntos básicos">Leyes de Identidad | \ (4.3.1\): Igualdades teóricas de conjuntos básicos\(\cap\) “>\(A \cap U = A\) | \ (4.3.1\): Igualdades teóricas de conjuntos básicos\(\cup\) “>\(A \cup ∅ = A\) |
| \ (4.3.1\): Igualdades teóricas de conjuntos básicos">Dominación | \ (4.3.1\): Igualdades teóricas de conjuntos básicos\(\cap\) “>\(A \cap ∅ = ∅\) | \ (4.3.1\): Igualdades teóricas de conjuntos básicos\(\cup\) “>\(A \cup U = U\) |
| \ (4.3.1\): Igualdades teóricas de conjuntos básicos">Idempotencia | \ (4.3.1\): Igualdades teóricas de conjuntos básicos\(\cap\) “>\(A \cap A = A\) | \ (4.3.1\): Igualdades teóricas de conjuntos básicos\(\cup\) “>\(A \cup A= A\) |
| \ (4.3.1\): Igualdades teóricas de conjuntos básicos">Absorción | \ (4.3.1\): Igualdades teóricas de conjuntos básicos\(\cap\) “>\(A \cap (A \cup B) = A\) | \ (4.3.1\): Igualdades teóricas de conjuntos básicos\(\cup\) “>\(A \cup (A \cap B) = A\) |
Antes de continuar mucho más en nuestro estudio de la teoría de conjuntos sería una buena idea darle un ejemplo. Vamos a probar la misma afirmación de dos maneras diferentes, una vez a través de la búsqueda de elementos y una vez usando las igualdades teóricas de conjunto básico de Table\(4.3.1\).
El comunicado que probaremos es\(A ∪ B = A ∪ (A ∩ B)\).
Primero, persiguiendo elementos:
Prueba: Supongamos que\(x\) es un elemento de\(A ∪ B\). Por la definición de unión sabemos que
\(x ∈ A ∨ x ∈ B.\)
La ley de identidad conjuntiva y el hecho de que\(x ∈ A ∨ x \notin A\) es una tautología nos da una afirmación lógica equivalente:\((x ∈ A ∨ x \notin A) ∧ (x ∈ A ∨ x ∈ B)\).
Por último, esta última afirmación equivale a
\(x ∈ A ∨ (x \notin A ∧ x ∈ B)\)
que es la definición de\(x ∈ A ∪ (A ∩ B)\).
Por otra parte, si asumimos eso\(x ∈ A ∪ (A ∩ B)\), se deduce que
\(x ∈ A ∨ (x \notin A ∧ x ∈ B).\)
Aplicando el derecho distributivo, la complementariedad disyuntiva y la ley de identidad, en secuencia obtenemos
\(\begin{array} x ∈ A ∨ (x \notin A ∧ x ∈ B) &\cong (x ∈ A ∨ x \notin A) ∧ (x ∈ A ∨ x ∈ B) \\ &\cong t ∧ (x ∈ A ∨ x ∈ B) \\ &\cong x ∈ A ∨ x ∈ B \end{array}\)
La última afirmación en esta cadena de equivalencias lógicas proporciona la definición de\(x ∈ A ∪ B\).
Q.E.D.
Una prueba de dos columnas de la misma afirmación se ve así:
Prueba:
\(A ∪ B \tag{Given} \)
\(= U ∩ (A ∪ B) \tag{Identity law} \)
\(= (A ∪ A) ∩ (A ∪ B) \tag{Complementarity}\)
\( = (A ∪ (A ∩ B) \tag{Distributive law}\)
Q.E.D.
Hay algunas nociones dentro de la teoría de conjuntos que no tienen ningún paralelismo claro en la Lógica. Una de ellas es esencialmente una generalización del concepto de “complementos”. Si piensas que el set A es la diferencia entre el set universal\(U\) y el set\(A\) estás en el camino correcto. La diferencia entre dos conjuntos está escrita\(A \setminus B\) (lamentablemente, a veces esto se denota usando el símbolo de resta ordinario\(A − B\)) y se define por
\(A \setminus B = A ∩ \overline{B}.\)
La diferencia,\(A \setminus B\), consiste en aquellos elementos de los\(A\) que no están en\(B\). En algunos desarrollos de la teoría de conjuntos, primero se define la diferencia de conjuntos y luego se define la complementación por\(A = U \setminus A\).
La diferencia de conjuntos (como la diferencia de números reales) no es una operación conmutativa. En otras palabras\(A \setminus B \neq B \setminus A\) (en general). Es posible definir una operación que actúe algo como la diferencia, pero que sea conmutativa. La diferencia simétrica de dos conjuntos se denota usando un triángulo (realmente un delta griego capital).
\[A \triangle B = (A \setminus B) ∪ (B \setminus A).\]
Demostrar que\(A \triangle B = (A \cup B) \setminus (A \cap B).\)
¡Vamos! ¡Leíste justo después de ese ejercicio sin siquiera hacer una pausa!
¿Qué? ¿Dices que lo intentaste y fue demasiado duro?
Bien, solo para ti (y esta vez sólo) he preparado una ayuda para ayudarte a pasar.
En la siguiente página hay una prueba de dos columnas del resultado que debes probar, pero las líneas de la prueba están todas revueltas. Haz una copia y corta todas las piezas y luego pégalas juntas en una prueba válida.
Entonces, no más excusas, ¡solo hazlo!
| \(= (A ∩ B) ∪ (B ∩ A)\) | Ley de Identidad |
| \(= (A ∪ B) ∩ (A ∩ B)\) | Def. de Diferencia Relativa |
| \((A ∪ B) \setminus (A ∩ B)\) | Dado |
| \(= ((A ∩ A) ∪ (A ∩ B)) ∪ ((B ∩ A) ∪ (B ∩ B))\) | Derecho Distributivo |
| \(= (A \setminus B) ∪ (B \setminus A)\) | Def. de Diferencia Relativa |
| \(= (A ∩ (A ∩ B)) ∪ (B ∩ (A ∩ B))\) | Derecho Distributivo |
| \(= A \triangle B\) | Def. de Diferencia Relativa |
| \(= (A ∩ (A ∪ B) ∪ (B ∩ (A ∪ B))\) | Ley de DeMorgan |
| \(= (∅ ∪ (A ∩ B)) ∪ ((B ∩ A) ∪ ∅)\) | Complementariedad |
Ejercicios:
Dejar\(A = \{1, 2, \{1, 2\}, b\}\) y dejar\(B = \{a, b, \{1, 2\}\}\). Encuentra lo siguiente:
- \(A ∩ B\)
- \(A ∪ B\)
- \(A \setminus B\)
- \(B \setminus A\)
- \(A \triangle B\)
En una baraja estándar de naipes, se pueden distinguir conjuntos basados en el valor nominal y/o el palo. Dejar\(A, 2, . . . 9, 10, J, Q\) y\(K\) representar los conjuntos de cartas que tienen los diversos valores de cara. También, dejar\(♥, ♠, ♣\) y\(♦\) ser los juegos de cartas teniendo los posibles trajes. Encuentra lo siguiente
- \(A ∩ ♥\)
- \(A ∪ ♥\)
- \(J ∩ (♠ ∪ ♥)\)
- \(K ∩ ♥\)
- \(A ∩ K\)
- \(A ∪ K\)
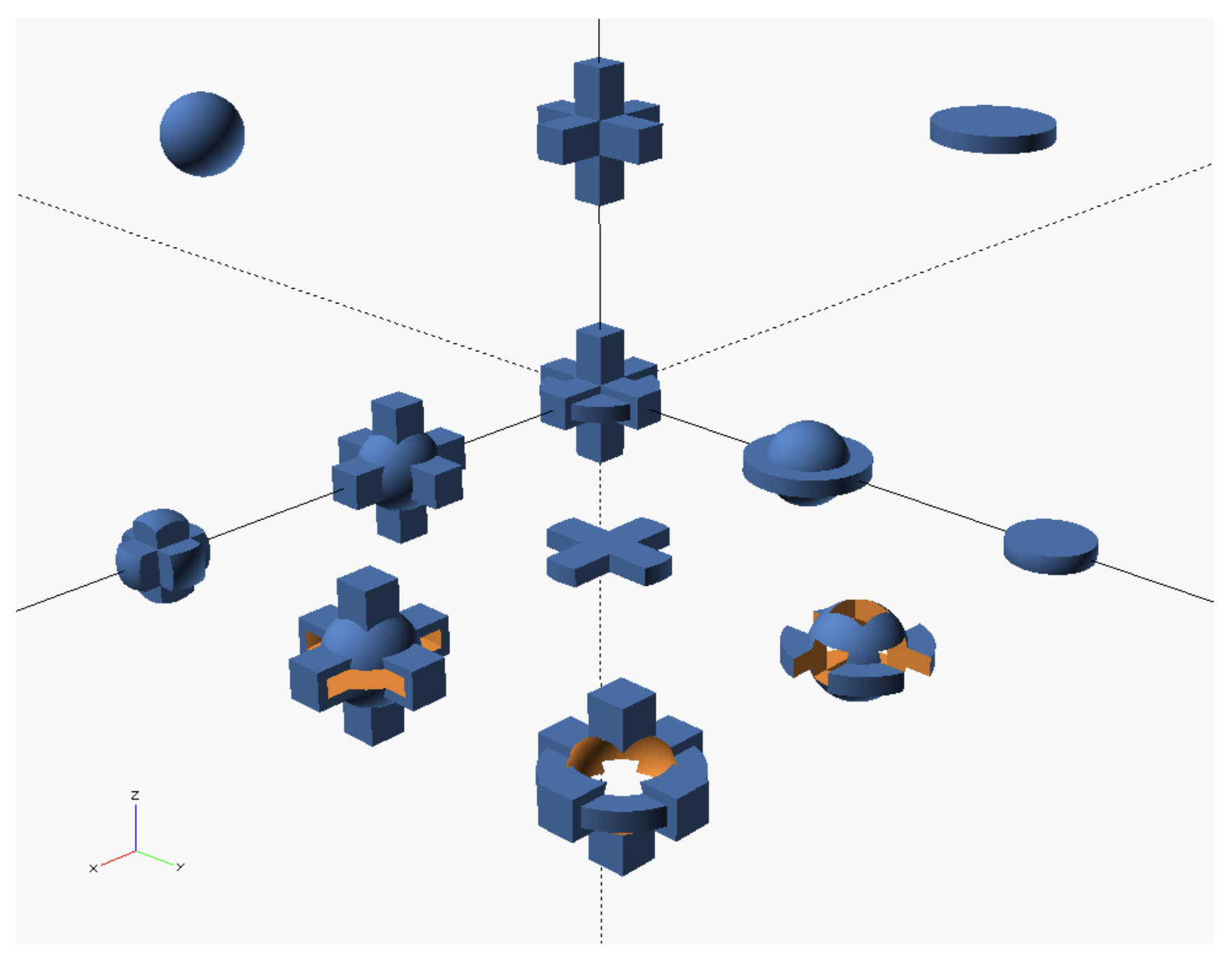
La siguiente es una captura de pantalla del programa de geometría computacional OpenSCAD (muy útil para hacer modelos para la impresión\(3\) -d.) En geometría computacional, utilizamos las operaciones de conjunto básico junto con algunos otros tipos de transformaciones para crear modelos interesantes utilizando componentes simples. Al otro lado de la parte superior de la imagen de abajo vemos\(3\) conjuntos de puntos en\(\mathbb{R}^3\), una bola, una especie de signo más\(3\) -dimensional, y un disco. Llamemos a la pelota\(A\), al signo más\(B\) y al disco\(C\). Las nueve formas que se muestran debajo de ellas están hechas de\(A\),\(B\) y\(C\) usando unión, intersección y diferencia de conjunto. ¡Identifícalos!
Hacer pruebas de búsqueda de elementos (mostrar que un elemento está en el lado izquierdo si y solo si está en el lado derecho) para probar cada una de las siguientes igualdades de conjunto.
- \(A ∩ B = A ∪ B\)
- \(A ∪ B = A ∪ (A ∩ B)\)
- \(A \triangle B = (A ∪ B) \setminus (A ∩ B)\)
- \((A ∪ B) \setminus C = (A \setminus C) ∪ (B \setminus C)\)
Para cada entero positivo\(n\), definiremos un intervalo\(I_n\) por
\(I_n = [−n, \dfrac{1}{n}).\)
Encuentra la unión e intersección de todos los intervalos en esta familia infinita.
\( \bigcup_{n∈ \mathbb{Z}^+} I_n =\)
\( \bigcap_{n∈ \mathbb{Z}^+} I_n =\)
Hay un conjunto\(X\) tal que, para todos los conjuntos\(A\), tenemos\(X \triangle A = A\). ¿Qué es\(X\)?
Hay un conjunto\(Y\) tal que, para todos los conjuntos\(A\), tenemos\(Y \triangle A = A\). ¿Qué es\(Y\)?
Al probar una identidad teórica de conjuntos, básicamente estamos demostrando que dos conjuntos son iguales. Una manera razonable de proceder es demostrar que cada uno está contenido en el otro. \(A ∩(B ∪ C) = (A ∩ B)∪(A ∩ C)\)Demuéstralo demostrando eso\(A∩(B ∪ C) ⊆ (A∩B)∪(A∩ C) and (A∩B)∪(A∩ C) ⊆ A ∩ (B ∪ C)\).
Demuéstralo\(A∪(B∩C) = (A∪B)∩(A∪C)\) demostrando eso\(A∪(B∩C) ⊆ (A ∪ B) ∩ (A ∪ C)\) y\((A ∪ B) ∩ (A ∪ C) ⊆ A ∪ (B ∩ C)\).
Demostrar las versiones teóricas de conjunto de las leyes de DeMorgan utilizando la técnica discutida en los problemas anteriores.
La técnica anterior (\(A = B\)demostrando que argumentando eso\(A ⊆ B ∧ B ⊆ A\)) tendrá un esquema algo así como
Prueba: Primero lo demostraremos\(A ⊆ B\).
Hacia ese fin, supongamos\(x ∈ A\)...
Así\(x ∈ B\).
Ahora, eso lo demostraremos\(B ⊆ A\).
Supongamos que\(x ∈ B\)...
Así\(x ∈ A\).
Por lo\(A ⊆ B ∧ B ⊆ A\) tanto así concluimos que\(A = B\).
Q.E.D.
Formular una prueba\(A \triangle B = (A ∪ B) \setminus (A ∩ B)\) que siga este esquema.