4.4: Diagramas de Venn
- Page ID
- 114139
Ojalá hayas visto diagramas de Venn antes, pero posiblemente no hayas pensado profundamente en ellos. Los diagramas de Venn aprovechan una propiedad obvia pero importante de las curvas cerradas dibujadas en el plano. Dividen los puntos del plano en dos conjuntos, ¡los que están dentro de la curva y los que están afuera! (Olvídate por un momento de los puntos que están en la curva.) Esta afirmación aparentemente obvia se conoce como el teorema de la curva de Jordania, y en realidad requiere algunos detalles. Una curva de Jordan es el tipo de curva que podrías dibujar si se requiere que termines donde empezaste y no cruzarás ninguna parte de la curva que ya se haya dibujado. En términos técnicos tal curva se llama continua, simple y cerrada. El teorema de la curva de Jordania es una de esas afirmaciones que apenas parece necesitar una prueba, pero sin embargo, la prueba de esta afirmación es probablemente la obra más recordada del famoso matemático francés Camille Jordan.
El diagrama prototípico de Venn es la imagen que se parece algo a la vista a través de un conjunto de binoculares.
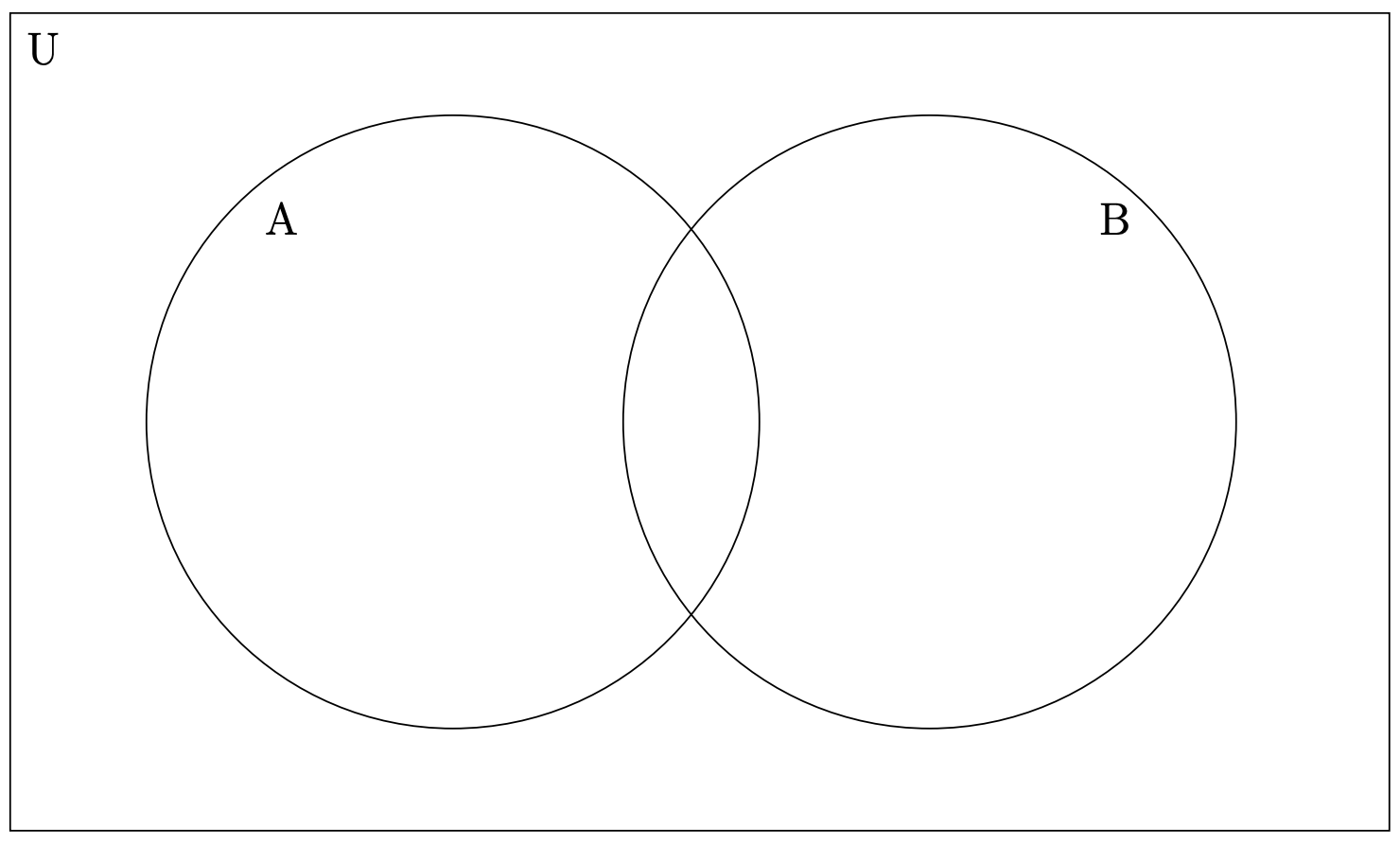
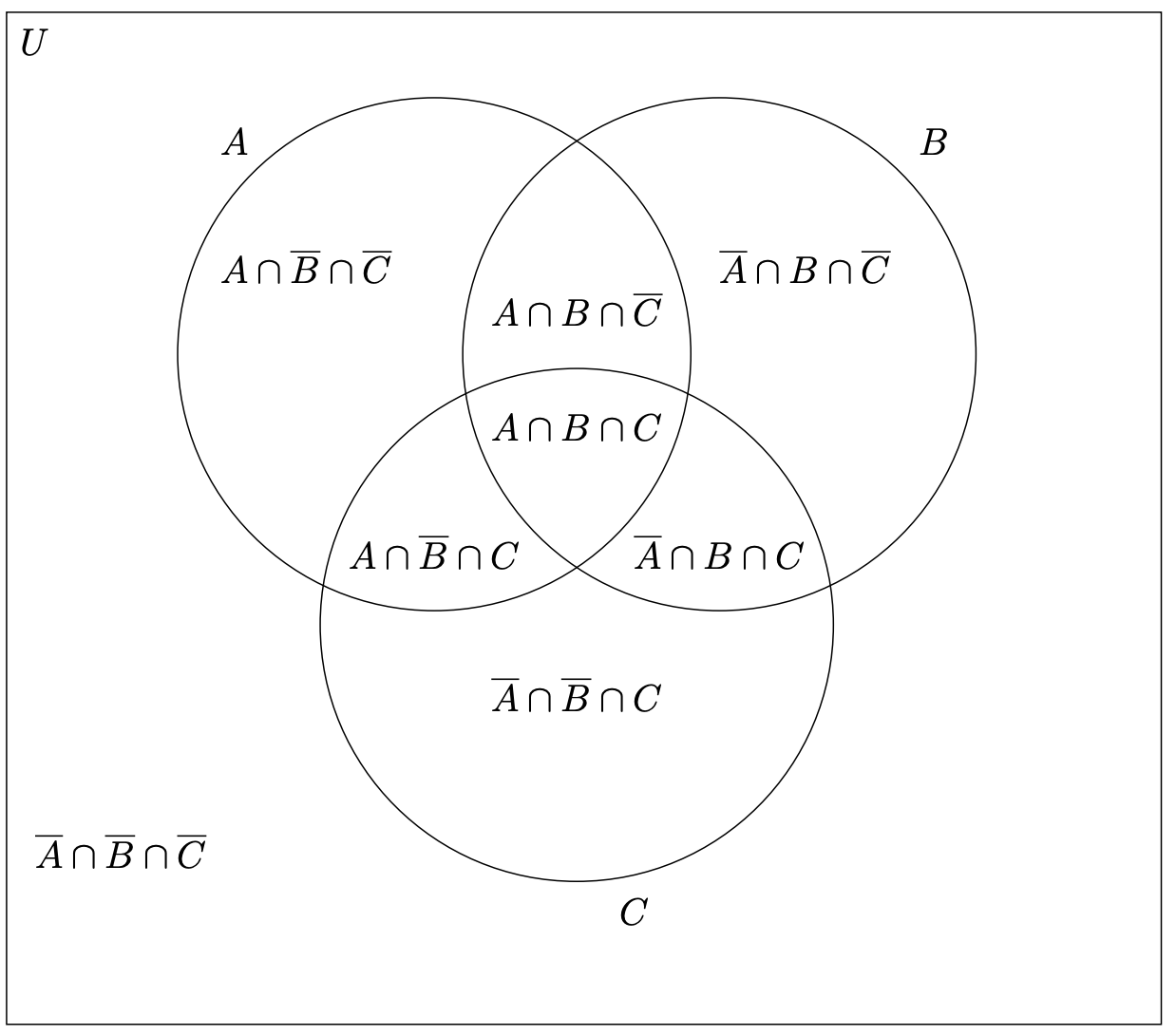
En un diagrama de Venn el universo del discurso se dibuja normalmente como una región rectangular dentro de la cual se produce toda la acción. Cada conjunto en un diagrama de Venn se representa dibujando una curva cerrada simple, ¡típicamente un círculo, pero no necesariamente! Por ejemplo, si quieres dibujar un diagrama de Venn que muestre todas las intersecciones posibles entre cuatro conjuntos, encontrarás que es imposible con (solo) círculos.
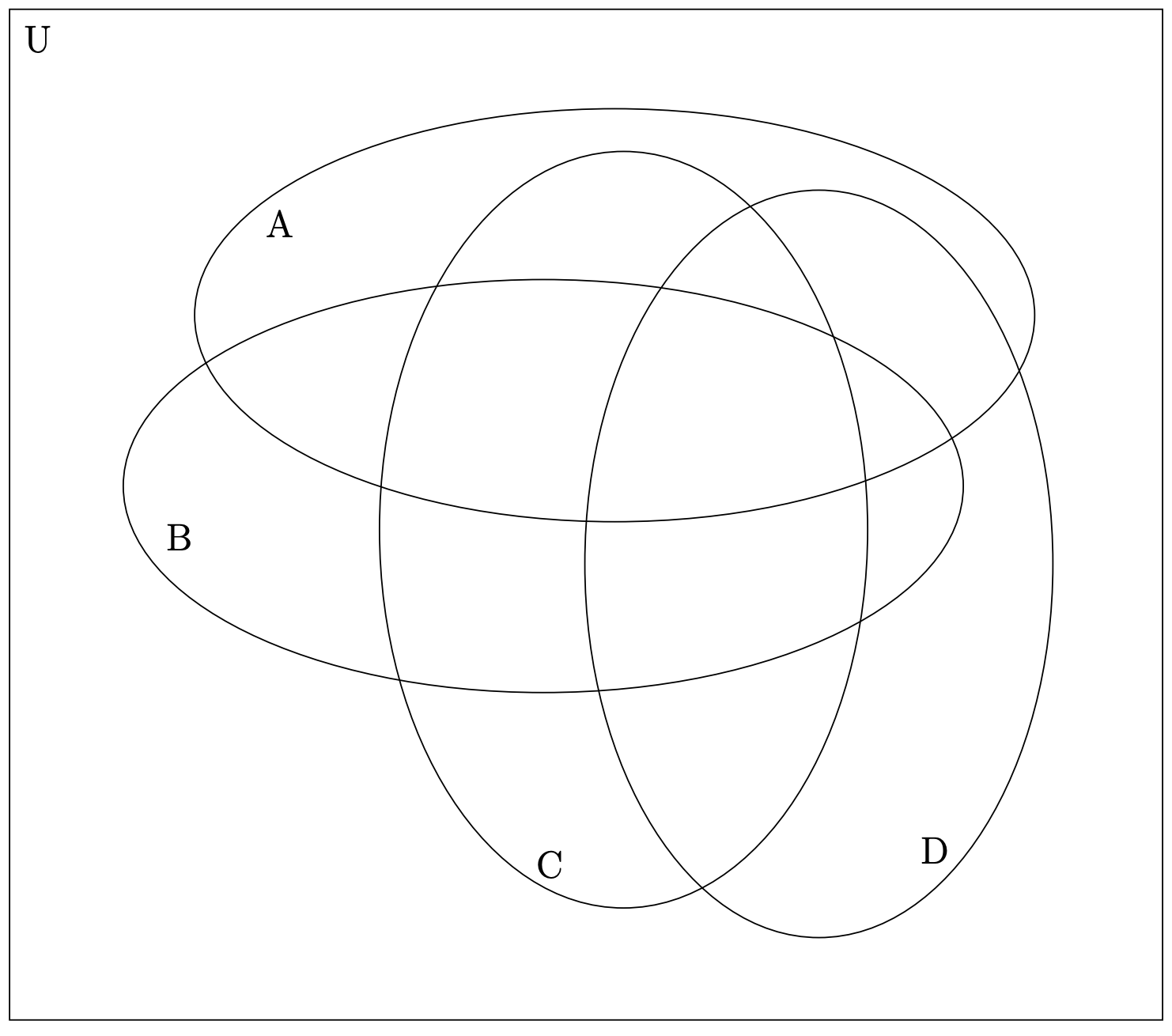
Verifique que el diagrama anterior tenga regiones que representen todas las intersecciones\(16\) posibles de\(4\) conjuntos
Hay un cierto “zen” a los diagramas de Venn que deben ser internalizados, pero una vez que lo hayas hecho, pueden ser utilizados para pensar de manera muy efectiva sobre las relaciones entre conjuntos. El trato principal es que los puntos dentro de una de las curvas cerradas simples no están necesariamente en el conjunto — solo algunos de los puntos dentro de una simple curva cerrada están en el conjunto, ¡y no sabemos exactamente dónde están! Las diversas curvas cerradas simples en un diagrama de Venn dividen el universo en un montón de regiones. Podría ser mejor pensar en estas regiones como áreas cercadas en las que se encuentran los elementos de un molino conjunto, al igual que los animales domesticados en sus corrales. Una de nuestras principales herramientas para trabajar con diagramas de Venn es deducir que algunas de estas regiones no contienen ningún elemento; luego marcamos esa región con el símbolo de conjunto vacío (\(∅\)).
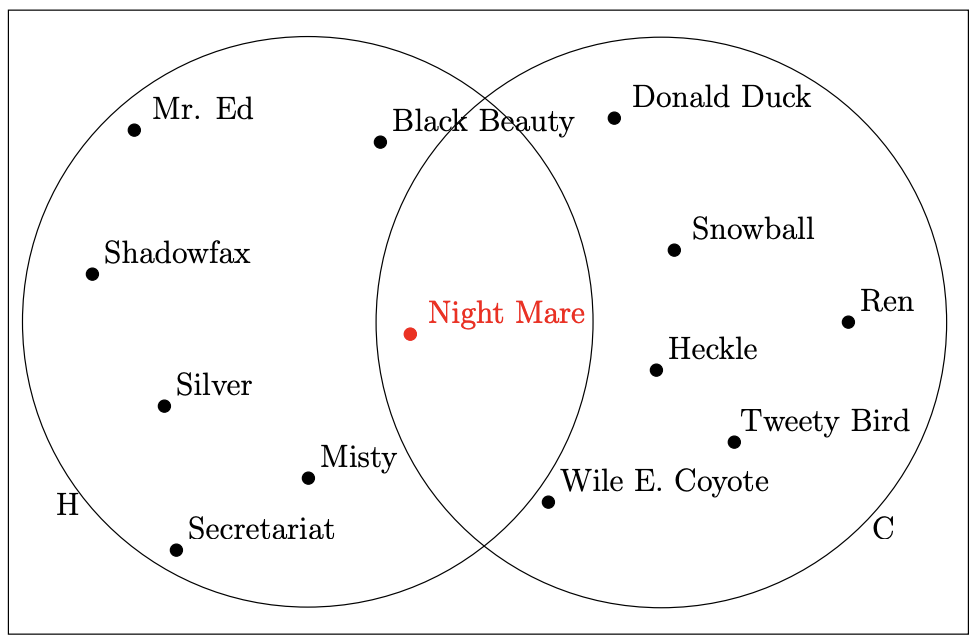
Aquí hay un pequeño ejemplo de un universo finito.
Y aquí está el mismo universo con algunas curvas de Jordan utilizadas para rodear dos subconjuntos.
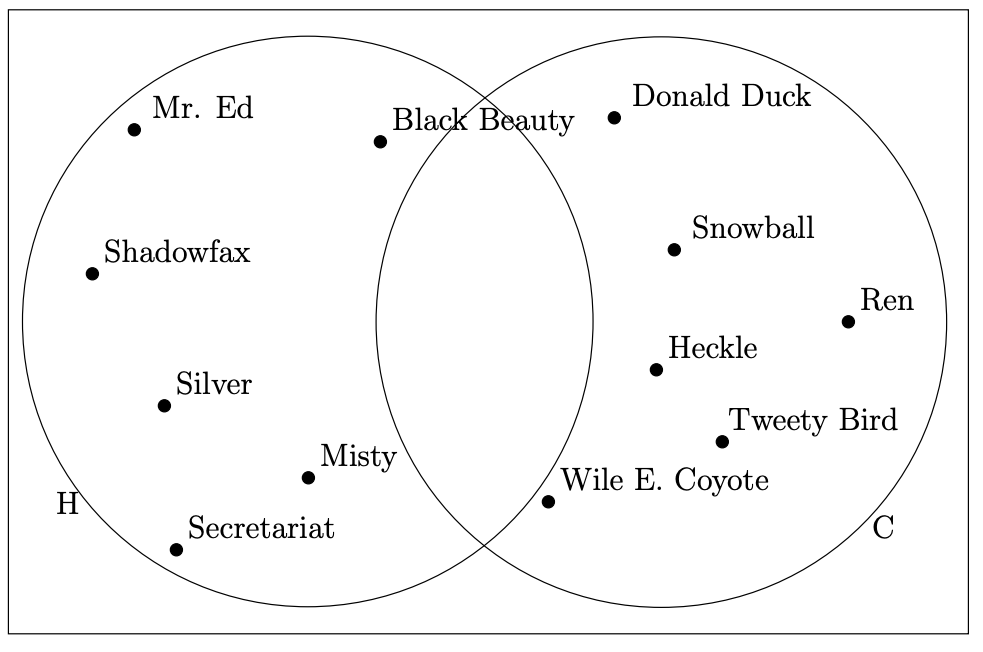
Esta imagen podría llevarnos a pensar que el conjunto de personajes de dibujos animados y el conjunto de caballos son disjuntos, por lo que pensamos que sería bueno agregar un elemento más a nuestro universo para disipar esa noción.
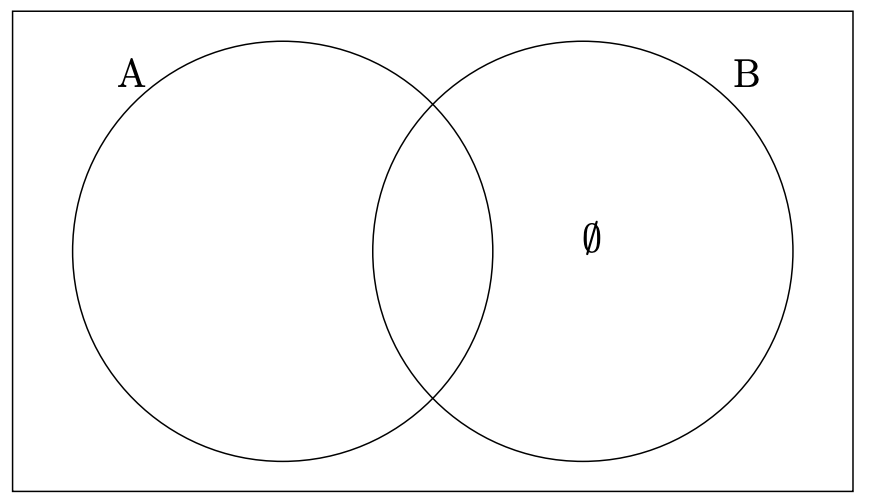
Supongamos que tenemos dos sets\(A\)\(B\) y y estamos interesados en demostrarlo\(B ⊆ A\). El trabajo está hecho si podemos demostrar que todos los\(B\) elementos están realmente en la región en forma de ojo que representa la intersección\(A ∩ B\). Es equivalente si podemos mostrar que la región marcada con\(∅\) en el siguiente diagrama está realmente vacía.
Vamos a armar todo esto. La inclusión\(B ⊆ A\) corresponde a la oración lógica\(M_B \implies M_A\). Sabemos que las implicaciones son equivalentes a las declaraciones OR, entonces\(M_B \implies M_A \cong ¬M_B ∨ M_A\). La noción de que la región que hemos indicado anteriormente está vacía se escribe como\(A ∩ B = ∅\), en términos lógicos esta es\(¬M_A ∧ M_B \cong c\). Por último, aplicamos la ley de DeMorgan y una conmutación para obtener\(¬M_B ∨M_A \cong t\). Debe tomar nota de la convención de que cuando vea una frase lógica recién escrita en la página (como es el caso de la primera frase de este párrafo) lo que se está afirmando es que la oración es universalmente cierta.\(M_B \implies M_A\) Así, escribir\(M_B \implies M_A\) es lo mismo que escribir\(M_B =\implies M_A \cong t\).
Se puede usar información que se conoce a priori cuando se dibuja un diagrama de Venn. Por ejemplo, si se sabe que dos conjuntos son disjuntos, o si se sabe que uno está contenido en el otro, podemos dibujar diagramas de Venn como los siguientes
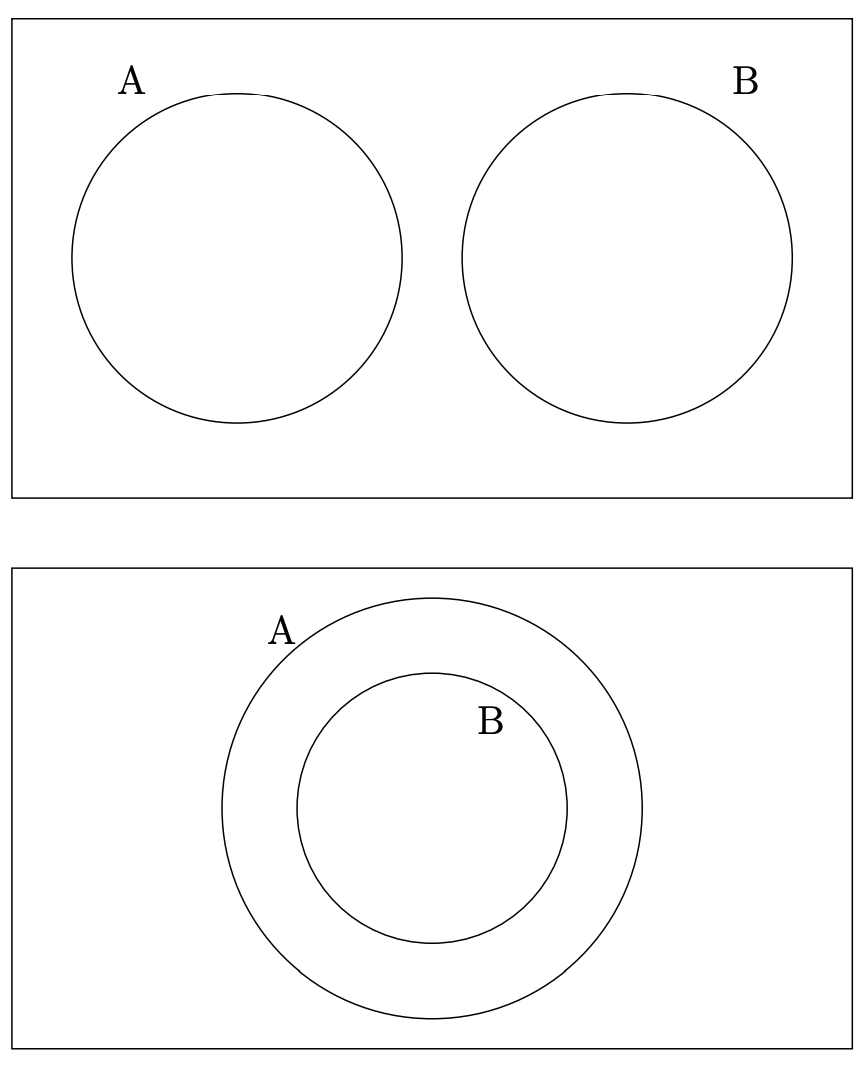
Sin embargo, ambas situaciones también se pueden tratar trabajando con diagramas de Venn en los que los conjuntos están en posición general —lo que en esta situación significa que se muestra cada intersección posible— y luego marcando con cualquier región vacía\(∅\).
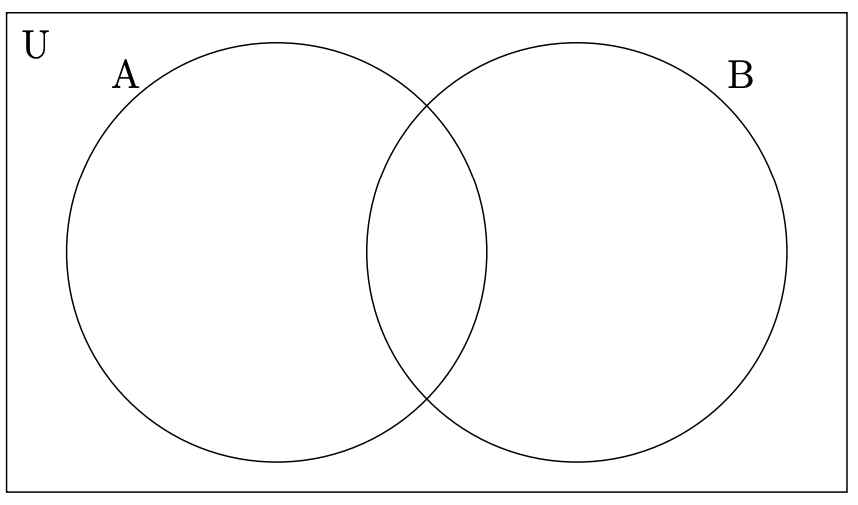
En un diagrama de Venn para dos conjuntos en posición general, indique las regiones vacías cuando
- Los conjuntos son disjuntos.
- \(A\)está contenido en\(B\).
Existe una conexión, quizás obvia, entre las regiones que vemos en un diagrama de Venn con conjuntos en posición general y los reconocedores que estudiamos en la sección sobre circuitos lógicos digitales. De hecho, ambos temas tienen que ver con la forma normal disyuntiva. En un diagrama de Venn con\(k\) sets, estamos viendo el universo del discurso desmontado en la unión de\(2^k\) regiones cada una de las cuales corresponde a una intersección de cualquiera de los conjuntos o su complemento. Una expresión arbitraria que involucra símbolos de teoría de conjuntos y estos\(k\) conjuntos es verdadera en algunas de estas\(2^k\) regiones y falsa en las otras. Hemos puesto la expresión arbitraria en forma normal disyuntiva cuando la expresamos como una unión de las intersecciones que describen esas regiones.
Ejercicios:
Vamos\(A = \{1, 2, 4, 5\}\),\(B = \{2, 3, 4, 6\}\), y\(C = \{1, 2, 3, 4\}\). Coloque cada uno de los elementos\(1, . . . , 6\) en las regiones apropiadas de un diagrama de Venn de tres conjuntos.
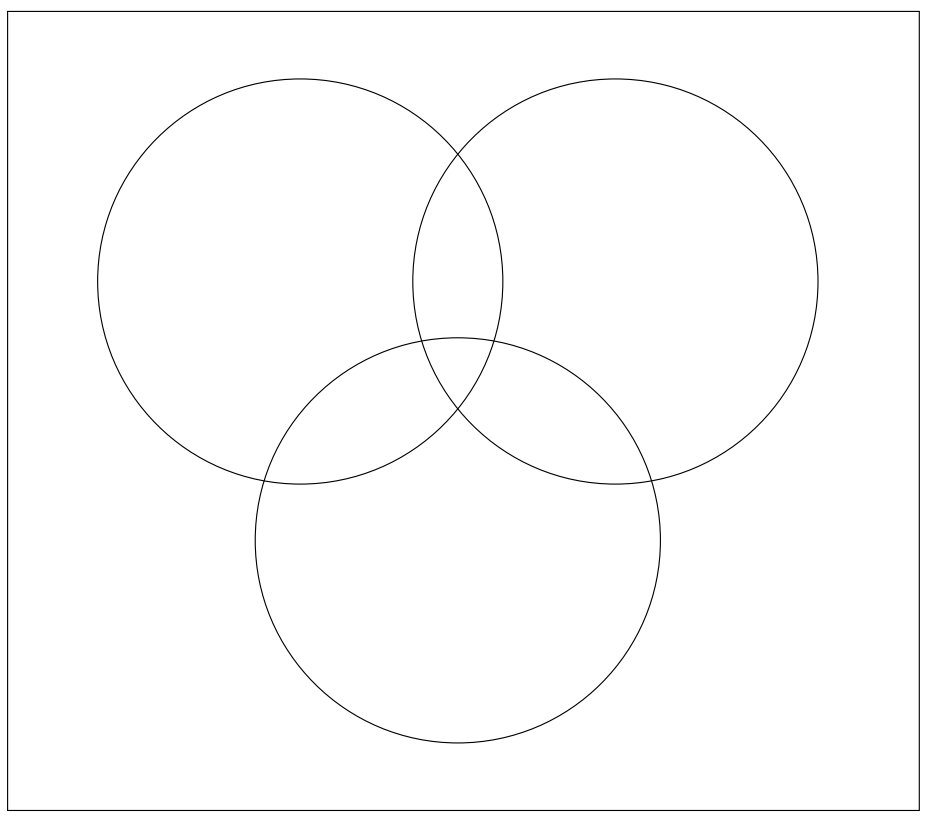
Demostrar o desacreditar:\((A ∩ C ⊆ B ∩ C) \implies A ⊆ B\)
Los diagramas de Venn generalmente se hacen usando curvas cerradas simples sin más restricciones. Intente crear diagramas de Venn para\(3\),\(4\) y\(5\) establece (en posición general) usando curvas cerradas simples rectangulares.
Llamamos a una curva rectilínea si está hecha de segmentos de línea que se encuentran en ángulo recto. Si alguna vez has jugado con un Etch-a-sketch sabrás a qué nos referimos con el término “rectilíneo”. El siguiente ejemplo de una curva rectilínea también puede ayudar a aclarar esta noción.
Utilice curvas cerradas simples rectilíneas para crear un diagrama de Venn para\(5\) conjuntos.
Argumentar por qué las curvas rectilíneas serán suficientes para construir cualquier diagrama de Venn.
Encuentra la forma normal disyuntiva de\(A ∩ (B ∪ C)\).
Encuentra la forma normal disyuntiva de\((A \triangle B) \triangle C\)
Los prototipos para las formas de argumento modus ponens y modus tollens son los siguientes:
Todos los hombres son mortales. Todos los hombres son mortales.
Sócrates es un hombre. y. Zeus no es mortal.
Por lo tanto Sócrates es mortal. Por lo tanto Zeus no es un hombre.
Ilustrar estos argumentos usando diagramas de Venn.
Usa diagramas de Venn para convencerte de la validez de la siguiente declaración de contención
\((A ∩ B) ∪ (C ∩ D) ⊆ (A ∪ C) ∩ (B ∪ D)\).
Ahora demuéstralo!
Utilice diagramas de Venn para mostrar que la siguiente equivalencia de conjunto es falsa.
\((A ∪ B) ∩ (C ∪ D) = (A ∪ C) ∩ (B ∪ D)\)