6.6: Funciones especiales
- Page ID
- 114099
Hay muchas funciones que fallan en la prueba de línea horizontal para la que, sin embargo, parece que tenemos funciones inversas para. Por ejemplo,\(x^2\) falla HLT pero\(\sqrt{x}\) es un inverso bastante razonable para ello; solo hay que tener cuidado con el problema de “más o menos”. Además,\(\sin x\) falla HLT bastante mal; cualquier línea horizontal\(y = c\) con\(−1 ≤ c ≤ 1\) golpeará\(\sin x\) infinitamente muchas veces. ¡Pero mira! Aquí mismo en mi calculadora hay un botón etiquetado como “\(\sin^{−1}\).” 1 Esta aparente contradicción puede resolverse utilizando la noción de restricción.
Dada una función\(f\) y un subconjunto\(D\) de su dominio, la restricción de\(f\) a\(D\) se denota\(f|_D\) y
\[f|_D = \{(x, y) x ∈ D ∧ (x, y) ∈ f\}.\]
La forma en que normalmente usamos la restricción es eliminar cualquier región en\(\text{Dom}(f)\) esa causa\(f\) que no sea uno a uno. Es decir, elegimos un subconjunto\(D ⊆ \text{Dom}(f)\) para que\(f|_D\) sea una inyección. Esto nos permite invertir la versión restringida de\(f\). Puede haber problemas al hacer esto, pero si tenemos cuidado con la forma en que elegimos\(D\), estos problemas suelen resolverse.
Supongamos que\(f\) es una función que no es uno a uno, y\(D\) es un subconjunto de\(\text{Dom}(f)\) tal que\(f|_D\) es uno a uno. La función restringida\(f|_D\) tiene una inversa que denotaremos por\(g\). Tenga en cuenta que\(g\) es una función de\(\text{Rng}(f|_D)\) a\(D\). ¿Cuál de los siguientes es siempre cierto:\(f(g(x)) = x\) o\(g(f(x)) = x\)?
Técnicamente, cuando hacemos el proceso descrito anteriormente (elegir un dominio\(D\) para que la restricción\(f|_D\) sea invertible, y encontramos esa inversa) la función que obtenemos es una inversa correcta para\(f\).
Echemos un vistazo más de cerca a la función sinusoidal inversa. Esto debería ayudarnos a entender realmente el concepto “inverso correcto”.
Un vistazo a la gráfica de sin duda nos\(y = \sin x\) convencerá de que esta función no es inyectable, sino que la parte de la gráfica que se muestra en negrita a continuación pasa la prueba de línea horizontal.
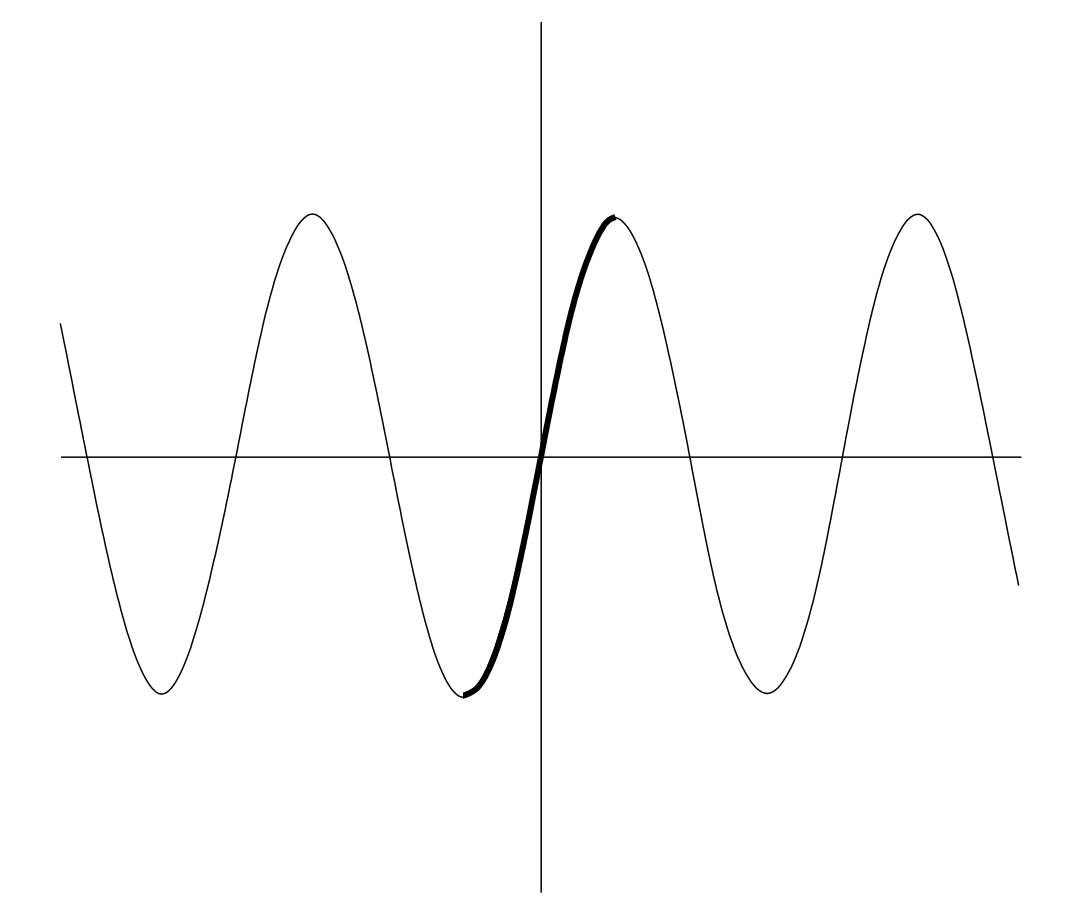
Si restringimos el dominio de la función sinusoidal al intervalo cerrado\( \left[ −\dfrac{π}{2}, \dfrac{π}{2} \right]\), tenemos una función invertible. La inversa de esta función restringida es la función que conocemos como\(\sin^{−1} (x)\) o\(\arcsin(x)\). El dominio y el rango de\(\sin^{−1} (x)\) son (respectivamente) los intervalos\([−1, 1]\) y\(\left[ −\dfrac{π}{2}, \dfrac{π}{2} \right]\).
Observe que si elegimos un número\(x\) en el rango\(−1 ≤ x ≤ 1\) y le aplicamos la función sinusoidal inversa, obtendremos un número entre\(-\dfrac{π}{2}\) y\(\dfrac{π}{2}\), es decir, un número que podemos interpretar como un ángulo en la medida de radianes. Si luego procedemos a calcular el seno de este ángulo, recuperaremos nuestro número original\(x\).
Por otro lado, si elegimos primero un ángulo, luego tomamos el seno del mismo para obtener un número\([−1, 1]\) y luego tomar el seno inverso de ese, solo terminaremos con el mismo ángulo con el que empezamos si elegimos el ángulo original para que quede en el intervalo\(\left[ −\dfrac{π}{2}, \dfrac{π}{2} \right]\).
Obtenemos un inverso correcto para la función coseno al restringirla al intervalo\([0, π]\). ¿Cuáles son el dominio y el rango de\(\cos^{−1}\)?
El mapa sinuoso es una función que va desde\(\mathbb{R}\) el círculo unitario en el\(y\) plano\(x\) —, definido por
\[W(t) = (\cos t, \sin t).\]
Uno puede pensar en este mapa como literalmente enrollar la línea real infinitamente larga alrededor y alrededor del círculo. Obviamente, esto no es una inyección — hay un número infinito de valores de\(t\) que se mapean a (por ejemplo) el punto\((1, 0)\),\(t\) puede ser cualquier entero múltiplo de\(2π\).
¿Cuál es el set\(W^{−1} (\{(0, 1)\})\)?
Si restringimos\(W\) al intervalo medio abierto\([0, 2π)\) la función restringida\(W [0,2π)\) es una inyección. La función inversa no es fácil de escribir, pero es posible expresar (en términos de las funciones inversas de seno y coseno) si consideramos los cuatro casos determinados por qué cuadrante puede encontrarse un punto en el círculo unitario.
Supongamos que\((x, y)\) representa un punto en el círculo unitario. Si\((x, y)\) pasa a estar en uno de los ejes de coordenadas tenemos
\(W^{−1} ((1, 0)) = 0\\ W^{−1} ((0, 1)) = \dfrac{π}{2} \\ W^{−1} ((−1, 0)) = π \\ W^{−1} ((0, −1)) = \dfrac{3π}{2}.\)
Si ni\(x\) ni\(y\) es cero, hay cuatro casos a considerar. Escribir una expresión para\(W^{−1} ((x, y))\) usar los casos
- \(x > 0 ∧ y > 0\),
- \(x < 0 ∧ y > 0\),
- \(x < 0 ∧ y < 0\)y
- \(x > 0 ∧ y < 0\).
Este último ejemplo que hemos hecho (el mapa sinuoso) fue inusual en que las salidas eran pares ordenados. Al pensar en este mapa como una relación (es decir, como un conjunto de pares ordenados) tenemos un par ordenado en el que el segundo elemento es un par ordenado! Solo por diversión, aquí hay otra forma de expresar el mapa sinuoso:
\[W = \{(t,(\cos t, \sin t)) t ∈ \mathbb{R}\}\]
Cuando se trata de expresiones muy complicadas que involucran pares ordenados, o más generalmente,\(n\) -tuplas ordenadas, es útil tener una manera de referirse sucintamente a las piezas de una tupla.
Empecemos por considerar el conjunto\(P = \mathbb{R} × \mathbb{R}\) —es decir,\(P\) es el\(y\) avión\(x\) —. Hay dos funciones, cuyo dominio es\(P\) que “escoger” el\(x\), y/o\(y\) coordinar. Estas funciones son llamadas\(π_1\) y\(π_2\),\(π_1\) es la proyección sobre la primera coordenada y\(π_2\) es la proyección sobre la segunda coordenada. 2
La función\(π_1 : \mathbb{R} × \mathbb{R} \implies \mathbb{R}\) conocida como proyección sobre la primera coordenada se define por
\[π_1((x, y)) = x.\]
La definición de\(π_2\) es totalmente análoga. Debe tener en cuenta que estas funciones de proyección son muy malas en lo que respecta a ser uno a uno. Por ejemplo, la preimagen de\(1\) debajo del mapa\(π_1\) consiste en todos los puntos de la línea vertical\(x = 1\). ¡Eso es un montón de preimágenes! Estos tipos están tan lejos de ser uno a uno que parece imposible pensar en una restricción apropiada que se vuelva invertible. Sin embargo, existe una función que proporciona un inverso correcto para ambos\(π_1\) y\(π_2\). Ahora, estos mapas de proyección van de\(\mathbb{R} × \mathbb{R}\) a\(\mathbb{R}\) así que una inversa tiene que ser un mapa de\(\mathbb{R}\) a\(\mathbb{R} × \mathbb{R}\). ¿Cuál es una manera razonable de producir un par de números reales si tenemos un solo número real en la mano? En realidad, hay muchas formas en las que se podría proceder, pero una opción razonable es crear un par donde el número de entrada aparezca en ambas coordenadas. Este es el llamado mapa diagonal,\(d : \mathbb{R} × \mathbb{R} \implies \mathbb{R}\), definido por\(d(a) = (a, a)\).
¿Cuál de los siguientes es siempre cierto,
\(d(π_1((x, y)) = (x, y)\)o\(π_1(d(x)) = x?\)
Hay algunas otras funciones que será conveniente introducir en esta etapa. Todos ellos son aspectos de la función característica de un subconjunto, así que comenzaremos con eso.
Siempre que tengamos una relación subconjunto/superconjunto,\(S ⊆ D\), es posible definir una función cuyo codominio es el\(\{0, 1\}\) que realiza una tarea muy útil — si\(x\) hay una entrada en el conjunto\(S\) la función lo indicará retornando\(1\), de lo contrario regresará\(0\). La función que tiene este comportamiento se conoce como\(1_S\), y se llama la función característica del subconjunto\(S\) (Hay quienes utilizan el término función indicadora de\(S\) for\(1_S\).) Por definición,\(D\) es el dominio de esta función.
\(1_S : D \implies \{0, 1\}\)
\[1_S(x)=\left\{ \begin{array}{ll} 1\;\;\;\; \text{ if } x ∈ S \\ 0\;\;\;\; \text{ otherwise} \end{array} \right.\]
Si tienes la función característica de un subconjunto\(S\), ¿cómo puedes crear la función característica de su complemento,\(\overline{S}\).
Una función característica puede considerarse como una encarnación de un criterio de pertenencia. La frase lógica abierta “\(x ∈ S\)” siendo verdadera es lo mismo que la ecuación “”\(1_S(x) = 1\). Hay una notación, que crece en popularidad, que hace lo mismo para una oración abierta arbitraria. La notación de corchetes Iverson usa la taquigrafía\([P(x)]\) para representar una función\(x\) que envía cualquiera que se haga\(P(x)\) fiel a\(1\), y cualquier entrada que haga\(P(x)\) false será enviada a\(0\).
\[ [P(x)]=\left\{ \begin{array}{ll} 1\;\;\;\; \text{ if } P(x) \\ 0\;\;\;\; \text{ otherwise} \end{array} \right. \]
Los corchetes de Iverson pueden ser particularmente útiles para expresar y simplificar sumas. Por ejemplo, podemos escribir\(\sum^{24}_{i=1} [2|i]\) para encontrar el número de números incluso naturales menores que\(25\). De igual manera, podemos escribir\(\sum^{24}_{i=1} [3|i]\) para encontrar el número de números naturales menores\(25\) que los que son divisibles por\(3\).
¿Qué cuenta la siguiente fórmula?
\(\sum^{24}_{i=1} [2|i] + [3|i] − [6|i]\)
Existe una notación mucho más venerable conocida como el delta de Kronecker que se puede considerar como un caso especial de la idea inherente a los corchetes de Iverson. Escribimos\(δ_{ij}\) como una taquigrafía para una función que toma dos entradas,\(δ(i, j)\) es\(1\) si y sólo si\(i\) y\(j\) son iguales.
\[ δ_{ij} =\left\{ \begin{array}{ll} 1\;\;\;\; \text{ if } i=j \\ 0\;\;\;\; \text{ otherwise} \end{array} \right. \]
El corchete de Iverson correspondiente sería simplemente\([i = j]\).
Terminaremos esta sección con una función que será especialmente importante en el Capítulo 8. Si tenemos un subconjunto arbitrario de los números naturales, podemos asociarlo con una cadena infinita\(0\) de s y\(1\) 's. pegando un punto decimal frente a tal cosa, obtenemos notación binaria para un número real en el intervalo\([0, 1]\). Hay un problema sutil que abordaremos cuando estudiemos esta función con más detalle en el Capítulo 8 — algunos números reales se pueden expresar de dos maneras diferentes en base\(2\). Por ejemplo, se\(\dfrac{1}{2}\) puede escribir como\(.1\) o como\(.01\) (donde, como de costumbre, el overline indica un patrón que se repite para siempre). Por el momento, estamos hablando de definir una función\(\phi\) cuyo dominio es\(\mathcal{P}(\mathbb{N})\) y cuyo codominio es el conjunto de todas las cadenas binarias infinitas. Denotemos estas expansiones binarias por. \(b_1b_2b_3b_4 . . .\). Supongamos que\(A\) es un subconjunto de\(\mathbb{N}\), entonces la expansión binaria asociada con\(A\) será determinada por\(b_i = 1_A(i)\). (Alternativamente, podemos usar la notación de corchetes Iverson:\(b_i = [i ∈ A]\).)
La función\(\phi\) definida en el último párrafo resulta ser una biyección — dado un subconjunto obtenemos una expansión binaria única, y dada la expansión binaria obtenemos (usando\(\phi^{-1}\)) un subconjunto único de\(\mathbb{N}\).
Algunos ejemplos probablemente ayudarán a aclarar el funcionamiento de esta función. Considera el conjunto\(\{1, 2, 3\} ⊆ \mathbb{N}\), la expansión binaria a la que esto corresponde tendrá\(1\)'s en las tres primeras posiciones después del decimal —\(\phi (\{1, 2, 3\}) = .111\) este es el número escrito\(.875\) en decimal. El número binario repetido infinito\(.01\) es la\(2\) representación base de\(\dfrac{1}{3}\), es fácil ver que .01 es la imagen del conjunto de naturales impares,\(\{1, 3, 5, . . .\}\).
Encuentra la representación binaria para el número real que es la imagen del conjunto de números pares bajo\(\phi\).
Encuentra la representación binaria para el número real que es la imagen del conjunto de números triangulares debajo\(\phi\). (Recordemos que los números triangulares son\(T = \{1, 3, 6, 10, 15, . . .\}\).)
Ejercicios:
El\(n\) -ésimo número triangular, denotado\(T(n)\), viene dado por la fórmula\(T(n) = \dfrac{(n^2 + n)}{2}\). Si consideramos esta fórmula como una función de\(\mathbb{R}\) a\(\mathbb{R}\), falla la prueba de línea horizontal y por lo tanto no es invertible. Encuentra una restricción adecuada para que\(T\) sea invertible.
El procedimiento algebraico habitual para invertir\(T(x) = \dfrac{(x^2+x)}{2}\) falla. Usa tu conocimiento de la geometría de las funciones y sus inversos para encontrar una fórmula para la inversa. (Pista: puede ser instructivo invertir primero la fórmula\(S(x) = \dfrac{x^2}{2}\) más simple, esto le dará el factor de escala vertical correcto).
¿Qué es\(π_2(W(t))\)?
Encuentra una inversa correcta para\(f(x) = |x|\).
En el espacio tridimensional, tenemos funciones de proyección que van sobre los tres ejes de coordenadas (\(π_1\),\(π_2\) y\(π_3\)) y también tenemos proyecciones sobre planos de coordenadas. Por ejemplo,\(π_{12}: \mathbb{R} × \mathbb{R} × \mathbb{R} \implies \mathbb{R} × \mathbb{R}\), definido por
\(π_{12}((x, y, z)) = (x, y)\)
es la proyección en el plano de\(y\) coordenadas\(x\) —. El triple de funciones\((\cos t, \sin t, t)\) es una expresión paramétrica para una hélice. Dejar\(H = \{(\cos t, \sin t, t) t ∈ \mathbb{R} \}\) ser el conjunto de todos los puntos en la hélice. ¿Cuál es el set\(π_{12}(H)\)? ¿Cuáles son los conjuntos\(π_{13}(H)\) y\(π_{23}(H)\)?
Considera el conjunto\(\{1, 2, 3, . . . , 10\}\). Expresar la función característica del subconjunto\(S = \{1, 2, 3\}\) como un conjunto de pares ordenados.
Si\(S\) y\(T\) son subconjuntos de un conjunto\(D\), ¿cuál es el producto de sus funciones características\(1_S · 1_T\)?
Evaluar la suma
\(\sum^{10}_{i=1} \dfrac{1}{i} · [i \text{ is prime}].\)