8.2: Ejemplos de equivalencia de conjuntos

Hay un enicillo milenario sobre lo que sucede cuando una fuerza irresistible se encuentra con un objeto inamovible. En un espíritu similar, a veces hay acalorados debates entre niños pequeños sobre qué superhéroe ganará una pelea. ¿Wolverine puede llevarse a Batman? ¿Y el Increíble Hulk contra la Cosa? Ciertamente, Superman está en lo más alto del montón en este orden. ¿O es él? ¿El hombre de acero incluso se involucraría en una pelea con una súper heroína femenina, dice Wonder Woman? (Recuerda las\(1950\) sensibilidades del alter ego de Clark Kent.)

A muchas personas el tema actual le parecerá tan sensato como las discusiones del patio escolar a las que se acaba de aludir. Nos preocupa saber si un conjunto infinito es más grande que otro, o son del mismo tamaño. Generalmente hay tres razones por las que la gente desdeña considerar este tipo de preguntas. El primero es que, al igual que los superhéroes, los sets infinitos son solo productos de la imaginación. La segunda es que no puede haber diferencia porque “infinito es infinito” —una vez que llegas al tamaño que llamamos infinito, no puedes agregar algo a eso para llegar a un infinito más grande. El tercero es que las respuestas a preguntas como esta no me van a ganar grandes montones de dinero así que “¿a quién le importa?”

El punto uno en realidad es bastante válido. Los físicos han determinado que parecemos habitar un universo de alcance finito, que contiene un número finito de partículas subatómicas, por lo que en realidad no puede haber conjuntos infinitos. Sin embargo, los axiomas que utilizamos para estudiar muchos campos de las matemáticas garantizan que los objetos de consideración sean infinitos en número. El infinito aparece como un concepto incluso cuando sabemos que no puede aparecer en la actualidad. Punto dos, el argumento de “sólo hay un tamaño de infinito” es incorrecto. Veremos un argumento informal que muestra que hay al menos dos tamaños de infinito, y un teorema más formal que muestra que en realidad hay una jerarquía infinita de infinidades en la Sección 8.3.

Punto tres, “¿a quién le importa?” es en cierto sentido el más difícil de tratar. Ojalá, disfrutes de los ingeniosos argumentos que vendrán por su propia belleza intrínseca. Pero, si puedes encontrar una manera de ganar grandes montones de dinero usando estas cosas, eso también estaría bien.

Empecemos.

¿Qué conjunto es más grande: los números naturales,\(\mathbb{N}\) o el conjunto\(\mathbb{E}^{\text{noneg}}\),, de números pares no negativos? Ambos son claramente infinitos, por lo que el campamento de “infinito es infinito” podría conducirse a la conclusión correcta a través del razonamiento inválido. Por otro lado, los números pares están contenidos en los números naturales así que hay un caso bastante convincente para decir que los pares son de alguna manera más pequeños que los naturales. La manera matemáticamente rigurosa de demostrar que estos conjuntos tienen la misma cardinalidad es mostrando una correspondencia uno a uno. Dado un número par, ¿cómo podemos producir un natural para emparejarlo? Y, dado un natural ¿cómo podemos producir un número par para emparejarlo? El mapa\(f : \mathbb{N} \implies \mathbb{E}^{\text{noneg}}\) definido por\(f(x) = 2x\) es claramente una función, y casi con la misma claridad, ¹ de inyección. ¿El mapa\(f\) también es una surjección? En otras palabras, ¿cada número par no negativo es la imagen de algún bajo natural\(f\)? Dado algún número par no negativo\(e\) necesitamos poder llegar a un\(x\) tal que\(f(x) = e\). Bueno, como\(e\) es un número par, por la definición de “par” sabemos que hay un entero\(k\) tal que\(e = 2k\) y como\(e\) es cero o positivo se deduce que también\(k\) debe ser\(0\) o positivo. Resulta que en realidad\(k\) es lo\(x\) que estamos buscando. Dicho de manera más sucinta, cada número par no negativo\(2k\) tiene una preimagen,\(k\), debajo del mapa\(f\). Así que\(f\) mapas\(\mathbb{N}\) surjectivamente sobre\(\mathbb{E}^{\text{noneg}}\). Ahora los sets que acabamos de considerar,

\(\mathbb{N} = \{0, 1, 2, 3, 4, 5, 6, . . .\}\)

y

\(\mathbb{E}^{\text{noneg}} = \{0, 2, 4, 6, 8, 10, 12, . . .\}\)

ambos tienen la característica de que se pueden enumerar —al menos en principio. Hay un primer elemento, seguido de un segundo elemento, seguido de un tercer elemento, etcétera, en cada conjunto. El siguiente set veremos,\(\mathbb{Z}\), no se puede enumerar tan fácilmente. Para enumerar los enteros necesitamos dejar que los punto-punto-puntos vayan tanto hacia adelante (hacia el infinito positivo) como hacia atrás (hacia el infinito negativo),

\(\mathbb{Z} = \{. . . , −3, −2, −1, 0, 1, 2, 3, . . .\}.\)

Demostrar que los números enteros son en realidad equinúmeros con los números naturales (que es lo que estamos a punto de hacer — y por cierto, ¿no es eso bastante notable?) necesitamos, esencialmente, encontrar una manera de enumerar los enteros en una lista infinita individual. Usando el símbolo ± podemos organizar una lista infinita individual, y si piensas en lo que significa el símbolo ±, probablemente se te ocurra

\(\mathbb{Z} = \{0, 1, −1, 2, −2, 3, −3, . . .\}.\)

Esta lista infinita de los enteros hace el trabajo que buscamos en cierto sentido: muestra una correspondencia uno a uno con\(\mathbb{N}\). De hecho, se puede pensar que cualquier listado infinito individual muestra una correspondencia uno a uno con\(\mathbb{N}\) — la primera entrada (¿o deberíamos decir entrada cero?) en la lista se corresponde con\(0\), se corresponde con la segunda entrada\(1\), y así sucesivamente.

\[\begin{array} 00\;\;\; &1\;\;\; &2\;\;\; &3\;\;\; &4\;\;\; &5\;\;\; &6\;\;\; &7\;\;\; &. . .\\ \updownarrow \;\;\;&\updownarrow \;\;\;&\updownarrow \;\;\;&\updownarrow \;\;\;&\updownarrow \;\;\;&\updownarrow \;\;\;&\updownarrow \\ 0 \;\;\;&1\;\;\; &−1 \;\;\;&2 \;\;\;&−2\;\;\; &3\;\;\; &−3\;\;\; &4\;\;\; &. . . \end{array} \]

Para hacer todo esto preciso necesitamos poder dar explícitamente la correspondencia oneto-one. No basta con tener una imagen de ello — necesitamos una fórmula. Observe que los enteros negativos están todos emparejados con naturales pares y los enteros positivos están todos emparejados con naturales impares. Esta observación nos lleva a una definición por partes de una función que da la biyección que buscamos

\[ f(x)=\left\{ \begin{array}{ll} −\dfrac{x}{2} \;\;\;\;\;\;\;\text{ if } x \text{ is even}\\ \dfrac{(x + 1)}{2}\;\; \text{ if } x \text{ is odd} \end{array} \right. \]

Por cierto, fíjense que ya que\(0\) es parejo cae en el primer caso, y afortunadamente esa fórmula le da el valor “correcto”.

Practica

La función inversa,\(f^{−1}\), también debe definirse por partes, pero en función de si la entrada es positiva o negativa. Definir la función inversa.

Los ejemplos que hemos hecho hasta ahora han demostrado que los enteros, los números naturales y los naturales pares tienen todos la misma cardinalidad. Este es el primer número cardinal infinito, conocido como\(ℵ_0\). En cierto sentido podríamos ver ambas equivalencias que hemos mostrado como demostrativas de eso\(2 ·∞ = ∞\). Nuestro siguiente ejemplo le dará crédito a la regla:\(∞ · ∞ = ∞\). El producto cartesiano de dos conjuntos finitos (el conjunto de todos los pares ordenados con entradas de los conjuntos en cuestión) tiene cardinalidad igual al producto de las cardinalidades de los conjuntos. ¿Qué supone que pasará si dejamos que los sets sean infinitos? Por ejemplo, ¿de qué es la cardinalidad\(\mathbb{N} × \mathbb{N}\)? Considera esto: el subconjunto de pares ordenados que comienzan con a\(0\) puede pensarse como una copia de\(\mathbb{N}\) sentarse dentro de este producto cartesiano. De hecho, el subconjunto de pares ordenados que comienzan con cualquier número en particular da otra copia del\(\mathbb{N}\) interior\(\mathbb{N} × \mathbb{N}\). Hay infinitamente muchas copias de\(\mathbb{N}\) sentarse dentro de\(\mathbb{N} × \mathbb{N}!\) Esto simplemente realmente debería llevarnos a una cardinalidad más grande. El sorprendente resultado de que no implica una idea a veces conocida como “La serpiente de Cantor” — un truco que nos permite enumerar los elementos de\(\mathbb{N} × \mathbb{N}\) en una lista individualmente infinita ². Se puede visualizar el conjunto\(\mathbb{N} × \mathbb{N}\) como los puntos que tienen coordenadas enteras en el primer cuadrante (junto con el origen y el positivo\(x\) y\(y\) los ejes). Este conjunto de puntos y el camino a través de ellos conocido como serpiente de Cantor se muestra en la Figura\(8.2.1\).

Figura\(\PageIndex{1}\): La serpiente de Cantor serpentea por el conjunto\(\mathbb{N} × \mathbb{N}\) encontrando sus elementos uno tras otro. (Copyright; autor vía fuente)

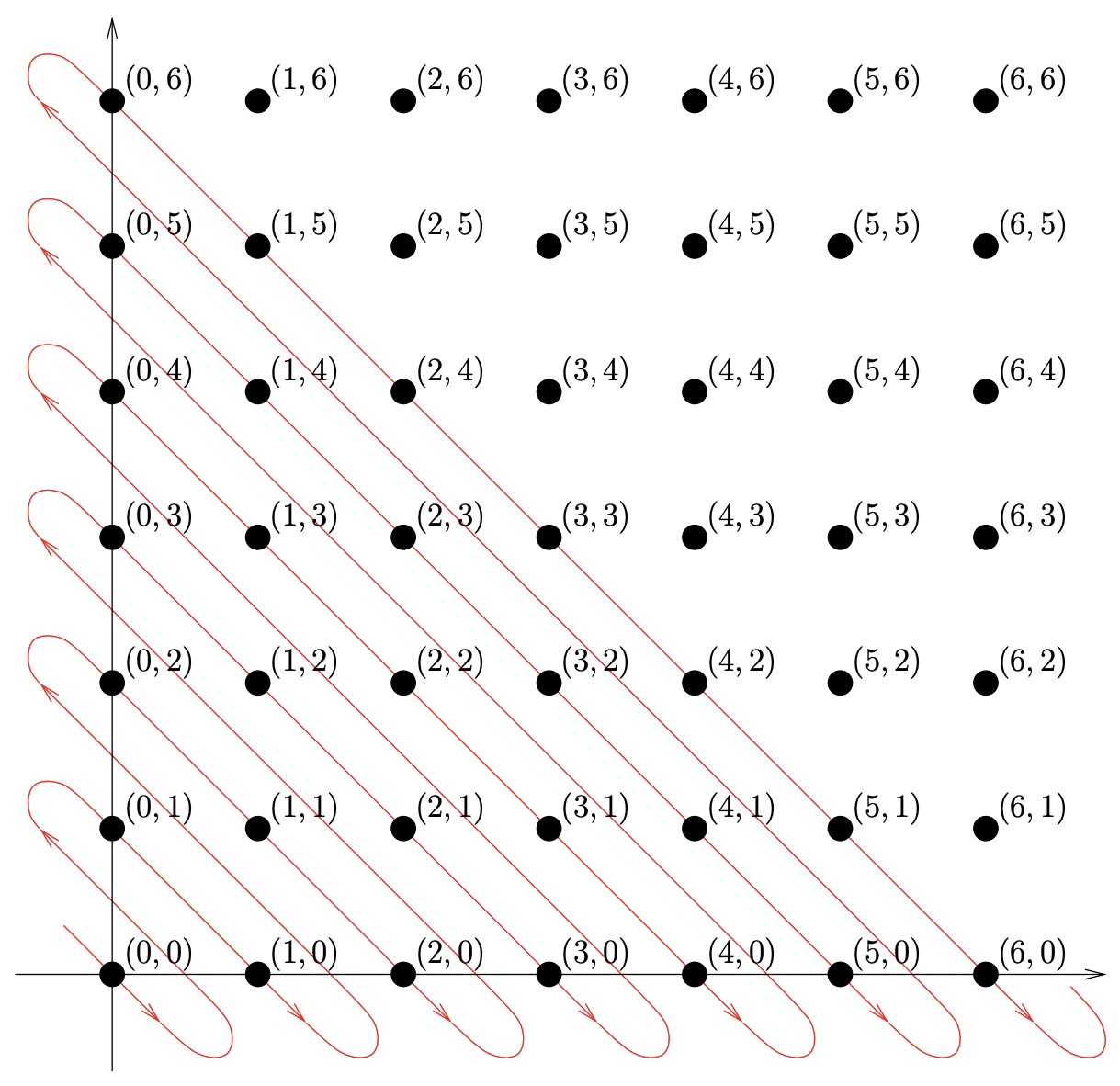
El diagrama de la Figura\(8.2.1\) da una forma visual de la correspondencia uno a uno que buscamos. En forma tabular, tendríamos algo como lo siguiente.

\[\begin{array} 00\;\;\; &1\;\;\; &2\;\;\; &3\;\;\; &4\;\;\; &5\;\;\; &6\;\;\; &7\;\;\;&8\;\;\; &. . .\\ \updownarrow \;\;\;&\updownarrow \;\;\;&\updownarrow \;\;\;&\updownarrow \;\;\;&\updownarrow \;\;\;&\updownarrow \;\;\;&\updownarrow\;\;\;&\updownarrow \;\;\;&\updownarrow \\ (0,0) \;\;\;&(0,1)\;\;\; &(1,0) \;\;\;&(0,2) \;\;\;&(1,1)\;\;\; &(2,0)\;\;\; &(0,3)\;\;\; &(1,2)\;\;\;&(2,1)\;\;\; &. . . \end{array} \]

Necesitamos producir una fórmula. En verdad, realmente deberíamos producir dos fórmulas. Uno que toma un par ordenado\((x, y)\) y produce un número\(n\). Otro que toma un número n y produce un par ordenado\((x, y)\) El número nos\(n\) dice dónde está el par (\(x, y)\)se encuentra en nuestro listado infinito. Sin embargo, hay un problema: la segunda fórmula (que da al mapa de\(\mathbb{N}\) a\(\mathbb{N} × \mathbb{N}\)) es muy difícil de escribir, es más fácil describir el mapa algorítmicamente. Una simple observación nos ayudará a deducir las diversas fórmulas. Los pares ordenados a lo largo del eje y (los de la forma (\(0\), algo)) corresponden a números triangulares. De hecho el par\((0, n)\) corresponderá al\(n\) -ésimo número triangular,\(T(n) = \dfrac{(n^2 + n)}{2}\). Los pares ordenados a lo largo de la línea inclinada descendente a partir de\((0, n)\) todos tienen la entidad de que es la suma de sus coordenadas\(n\) (porque a medida que la\(x\) coordenada -aumenta, la\(y\) coordenada -disminuye). Entonces, dado un par ordenado\((x, y)\), el número correspondiente a la posición en el extremo superior de la línea inclinada en la que se encuentra (que tendrá coordenadas\((0, x+y))\) serán\(T(x+y)\), y el par\((x, y)\) se produce en el listado exactamente\(x\) las posiciones posteriores\((0, x + y)\). Por lo tanto, la función\(f : \mathbb{N} × \mathbb{N} \implies \mathbb{N}\) viene dada por

\[f(x, y) = x + T(x + y) = x + \dfrac{(x + y)^2 + (x + y)}{2} .\]

Para ir en la otra dirección —es decir, tomar una posición en el listado y derivar un par ordenado— necesitamos averiguar dónde se encuentra un número dado relativo a los números triangulares. Por ejemplo, trate de averiguar con qué número de posición de\((x, y)\) par\(13\) se corresponderá. Bueno, el siguiente número triangular más pequeño es\(10\) que es\(T(4)\), así\(13\) será el número de un par ordenado a lo largo de la línea descendente cuya\(y\) -intercepción es\(4\). De hecho, se\(13\) emparejará con un par ordenado que tenga un\(3\) en la\(x\) coordenada (ya que\(13\) es\(3\) mayor que\(10\)) por lo que se deduce que\(f^{−1} (13) = (3, 1)\).

Por supuesto que tenemos que generalizar este procedimiento. Una de las partes más difíciles de encontrar esa generalización es encontrar el número\(4\) en el ejemplo anterior (cuando simplemente nos damos cuenta de eso\(T(4) = 10\)). Lo que realmente estamos haciendo ahí es invertir la función\(T(n)\). Encontrar un inverso para\(T(n) = \dfrac{(n^2+n)}{2}\) fue la esencia de uno de los ejercicios de la Sección 6.6. La parábola\(y = \dfrac{(x^2 + x)}{2}\) tiene raíces en\(0\)\(−1\) y se escala por un factor\(\dfrac{1}{2}\) relativo a la parábola “estándar”\(y = x^2\). Su vértice está en (\(−\dfrac{1}{2}, −\dfrac{1}{8})\). La gráfica de la relación inversa se obtiene, por supuesto, reflejando a través de la línea\(y = x\) y considerando escalado y traducciones horizontal/vertical podemos deducir una fórmula para una función que da un inverso correcto para\(T\),

\[T^{−1} (x) = \sqrt{2x + \dfrac{1}{4}} − \dfrac{1}{2}.\]

Entonces, dada\(n\), una posición en el listado, calculamos\(A = \left\lfloor \sqrt{2n + \dfrac{1}{4}} − \dfrac{1}{2} \right\rfloor\). La\(x\) coordenada -de nuestro par ordenado es\(n−T(A)\) y la\(y\) -coordenada es\(A−x\). No es bonito, pero la discusión anterior puede traducirse en una fórmula para\(f^{−1}\).

\[f^{−1} (n) = \left( n − \dfrac{\left\lfloor \sqrt{2n + \dfrac{1}{4}} − \dfrac{1}{2} \right\rfloor^2 + \left\lfloor \sqrt{2n + \dfrac{1}{4}} − \dfrac{1}{2} \right\rfloor}{2} , \left\lfloor \sqrt{2n + \dfrac{1}{4}} − \dfrac{1}{2} \right\rfloor − n + \dfrac{\left\lfloor \sqrt{2n + \dfrac{1}{4}} − \dfrac{1}{2} \right\rfloor^2 + \left\lfloor \sqrt{2n + \dfrac{1}{4}} − \dfrac{1}{2} \right\rfloor}{2} \right).\]

Cuando se restringen a los conjuntos apropiados (el dominio\(f\) está restringido a\(\mathbb{N}×\mathbb{N}\) y\(f^{−1}\) el dominio está restringido a\(\mathbb{N}\)), estas funciones son inversas de dos lados entre sí. Ese hecho es suficiente para demostrar que\(f\) es biyectiva. Hasta el momento hemos demostrado que los conjuntos\(\mathbb{E}^{\text{noneg}}, \(\mathbb{N}\),\(\mathbb{Z}\) y\(\mathbb{N} × \mathbb{N}\) todos tienen la misma cardinalidad —\(ℵ_0\). Planeamos aportar un argumento de que en realidad hay otros cardenales infinitos en la siguiente sección. Antes de dejar el tema actual (ejemplos de equivalencia de conjuntos) nos gustaría presentar otra técnica agradable para derivar las correspondencias biyectivas que utilizamos para mostrar que los conjuntos son equivalentes: las construcciones geométricas. Considera el conjunto de puntos en el segmento de línea\([0, 1]\). Ahora considere el conjunto de puntos en el segmento de línea\([0, 2]\). Este segmento de segunda línea, al ser el doble de largo que el primero, debe tener muchos más puntos en él. ¿Correcto?

Bueno, a lo mejor te estás acostumbrando a este tipo de cosas. El intervalo\([0, 1]\) es un subconjunto del intervalo\([0, 2]\), pero como ambos representan conjuntos infinitos de puntos es posible que en realidad tengan la misma cardinalidad. Podemos demostrar que esto es así usando una técnica geométrica. Posicionamos los segmentos de línea apropiadamente y luego usamos la proyección desde un punto cuidadosamente elegido para desarrollar una biyección. Imagínese ambos intervalos como tumbados sobre el\(x\) eje -en el\(y\) plano\(x\) -. Desplaza el intervalo más pequeño hacia arriba una unidad para que quede en la línea\(y = 1\). Ahora, usa proyección desde el punto\((0, 2)\), para visualizar la correspondencia ver Figura\(8.2.2\).

Figura\(\PageIndex{2}\): La proyección desde un punto se puede utilizar para mostrar que los intervalos de diferentes longitudes contienen el mismo número de puntos. (Copyright; autor vía fuente)

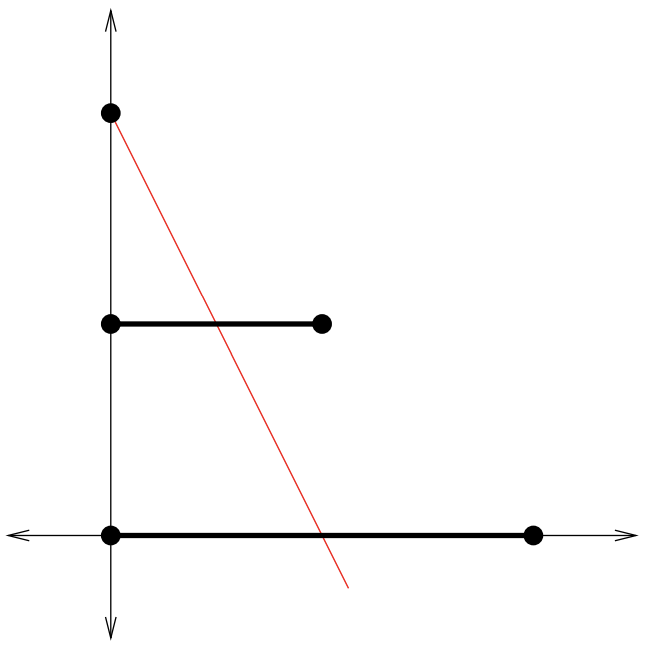
Al considerar proyecciones apropiadas podemos probar que dos intervalos arbitrarios cualesquiera (digamos\([a, b]\) y\([c, d]\)) ¡tienen las mismas cardinalidades! Tampoco es tan difícil derivar una fórmula para una función biyectiva entre dos intervalos.

\[f(x) = c + \dfrac{(x − a)(d − c)}{(b − a)}\]

Hay otras construcciones geométricas que podemos usar para mostrar que hay el mismo número de puntos en una variedad de entidades. Por ejemplo, considere la mitad superior del círculo unitario (¿Recuerdas el círculo unitario de Trig? Todos los puntos\((x, y)\) satisfactorios\(x^2 + y^2 = 1\).) Se trata de un semicírculo que tiene un radio de\(1\), por lo que la longitud del arco de dicho semicírculo es\(π\). No es difícil imaginar que este arco semicircular contenga el mismo número de puntos que un intervalo de longitud\(π\), y ya hemos argumentado que todos los intervalos contienen el mismo número de puntos. Pero, un buen ejemplo de proyección geométrica —proyección vertical (a.k.a.\(π_1\)) — se puede usar para mostrar que (por ejemplo) el intervalo\((−1, 1)\) y la porción del círculo unitario que se encuentra en el medio plano superior son equinúmeros.

Figura\(\PageIndex{3}\): La proyección vertical proporciona una correspondencia biyectiva entre un intervalo y un semicírculo. (Copyright; autor vía fuente)

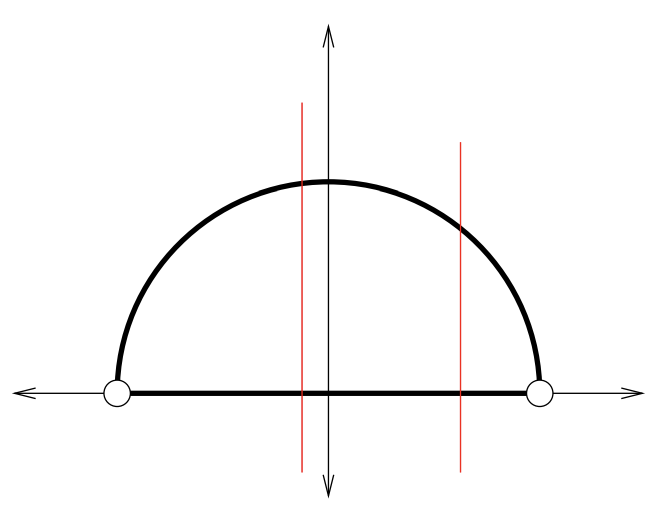
Una vez que la biyección se entiende geométricamente es bastante sencillo proporcionar fórmulas. Para pasar del semicírculo al intervalo, simplemente nos olvidamos de la\(y\) coordenada -:

\[f(x, y) = x.\]

Para ir en la otra dirección necesitamos recalcular el\(y\) valor -faltante:

\[f^{−1} (x) = (x, \sqrt{1 − x^2}).\]

Ahora estamos listos para juntar algunas de estas ideas para demostrar algo realmente bastante notable. Puede estar bien decir que los segmentos de línea de diferentes longitudes son equinúmeros —aunque la intuición de unos todavía se resiente ante la idea de que una línea de una milla de largo solo tiene el mismo número de puntos en ella que una línea de una pulgada de largo (o, si lo prefiere, hacer que sea un centímetro frente a un kilómetro). ¿Creerías que toda la línea —esa es la línea infinitamente extendida— no tiene más puntos en ella que un pequeño segmento? Deberías estar listo para probarlo tú mismo.

Practica

Encuentra un punto tal que la proyección desde ese punto determine una correspondencia uno a uno entre la porción del círculo unitario en el medio plano superior y la línea\(y = 1\).

En los ejercicios de la Sección 8.1 se suponía que debía demostrar que la equivalencia establecida es una relación de equivalencia. Parte de esa prueba debería haber sido demostrar que la relación es transitiva, y eso realmente solo se reduce a demostrar que la composición de dos bijecciones es en sí misma una bijección. Si no lo lograste a través de ese ejercicio dale otra oportunidad ahora, pero ya sea que puedas o no terminar esa prueba debería ser evidente lo que significa esa transitividad para nosotros en la situación actual. Cualquier par de segmentos de línea tiene el mismo tamaño — un segmento de línea (es decir, un intervalo) y un semicírculo tienen el mismo tamaño — el semicírculo y una línea infinita son del mismo tamaño — la transitividad nos dice que una línea infinitamente extendida tiene el mismo número de puntos que (por ejemplo) el intervalo\((0, 1)\).

Ejercicios:

Ejercicio\(\PageIndex{1}\)

Demostrar que los números positivos de la forma\(3k + 1\) son equinúmeros con los números positivos de la forma\(4k + 2\).

Ejercicio\(\PageIndex{2}\)

Demostrar que\(f(x) = c + \dfrac{(x − a)(d − c)}{(b − a)}\) proporciona una bijección desde el intervalo\([a, b]\) hasta el intervalo\([c, d]\).

Ejercicio\(\PageIndex{3}\)

Demostrar que dos círculos cualesquiera son equinúmeros (como conjuntos de puntos).

Ejercicio\(\PageIndex{4}\)

Determinar una fórmula para la biyección desde\((−1, 1)\) la línea\(y = 1\) determinada por proyección vertical sobre la mitad superior del círculo unitario, seguida de proyección desde el punto\((0, 0)\).

Ejercicio\(\PageIndex{5}\)

Es posible generalizar el argumento que muestra que un segmento de línea es equivalente a una línea a dimensiones superiores. En dos dimensiones mostraríamos que el disco unitario (el interior del círculo unitario) es equinumero con todo el plano\(\mathbb{R} × \mathbb{R}\). En tres dimensiones mostraríamos que la bola unitaria (el interior de la esfera unitaria) es equinumera con todo el espacio\(\mathbb{R}^3 = \mathbb{R} × \mathbb{R} × \mathbb{R}\). Aquí nos gustaría que pruebes el caso bidimensional.

La proyección gnomónica es un estilo de representación de mapa en el que una porción de una esfera se proyecta sobre un plano que es tangente a la esfera. El centro de la esfera se utiliza como punto desde el que se proyecta. Combine la proyección vertical desde el disco unitario en el\(y\) plano\(x\) — hasta la mitad superior de la esfera unitaria\(x^2 + y^2 + z^2 = 1\), con proyección gnomónica desde la esfera unitaria al plano\(z = 1\), para deducir una biyección entre el disco unitario y el plano (infinito).

Notas

1. Si\(x\) y\(y\) son diferentes números que se mapean al mismo valor, entonces\(f(x) = f(y)\) así\(2x = 2y\). Pero podemos cancelar los\(2\)'s y derivar eso\(x = y\), lo cual es una contradicción.

2. La serpiente de Cantor fue creada originalmente para mostrar eso\(\mathbb{Q}^{\text{noneg}}\) y\(\mathbb{N}\) son equinúmeras. Esta función se introdujo en los ejercicios de la Sección 6.5. La versión que presentamos aquí evita ciertas complicaciones.