8.4: Dominio
- Page ID
- 114115
Hemos dicho mucho sobre la relación de equivalencia determinada por la definición de equivalencia establecida por Cantor. También, ocasionalmente, hemos escrito cosas como\(|A| < |B|\), sin ser particularmente claros sobre lo que eso significa. Ahora es el momento de aclararse. En realidad existe una noción (quizás) más fundamental utilizada para comparar tamaños de conjuntos que equivalencia — dominancia. El dominio es una relación de orden en la clase de todos los conjuntos. Probablemente se debería definir primero el dominio y luego definir la equivalencia establecida en términos de ello. No hemos seguido ese plan por (al menos) dos razones. Primero, muchas personas pueden querer saltarse esta sección —los resultados de esta sección dependen del difícil teorema de Cantor-Bernstein-Schröder 1. En segundo lugar, posteriormente consideraremos que el dominio debería considerarse realmente como una relación de orden en el conjunto de todos los números cardinales —es decir, las clases de equivalencia de la relación de equivalencia de conjunto— y no en la colección de todos los conjuntos. Desde esa perspectiva, la equivalencia de conjunto realmente necesita definirse antes del dominio.
Se dice que un conjunto domina a otro si hay una función de este último al primero. De manera más formal, tenemos los siguientes
Si A y B son conjuntos, decimos “\(A\)domina\(B\)” y escribimos\(|A| > |B|\) iff hay una función de inyección\(f\) con dominio\(B\) y codominio\(A\).
Es fácil ver que esta relación es reflexiva y transitiva. El teorema de Cantor-Bernstein-Schröder demuestra que también es antisimétrico —lo que significa que el dominio es una relación ordenadora. Tenga en cuenta que aquí hay un abuso de terminología que hay que tener cuidado — ¿cuáles son el dominio y el alcance de la relación de “dominancia”? La definición nos llevaría a pensar que los sets son las cosas que van a ambos lados de la relación de “dominancia”, pero la notación es un poco más honesta, “\(|A| > |B|\)” indica que las cosas que realmente se comparan son los números cardinales de conjuntos (no los propios conjuntos). Así, la antisimetría para esta relación es
\[(|A| > |B|) ∧ (|B| > |A|) \implies (|A| = |B|).\]
En otras palabras, si\(A\) domina\(B\) y viceversa, entonces\(A\) y\(B\) son conjuntos equivalentes —una interpretación estricta de la antisimetría para esta relación podría llevar a la conclusión de que\(A\) y\(B\) son en realidad el mismo conjunto, lo cual es claramente un absurdo.
Naturalmente, queremos probar el teorema de Cantor-Bernstein-Schröder (que vamos a empezar a llamar el teorema C-B-S por brevedad), pero primero será instructivo mirar algunas de sus consecuencias. Una vez que tenemos el teorema C-B-S obtenemos un atajo muy útil para probar equivalencias establecidas. Dados conjuntos\(A\) y\(B\), si podemos encontrar funciones inyectoras que van entre ellos en ambas direcciones, sabremos que son equivalentes. Entonces, por ejemplo, podemos usar C-B-S para demostrar que el conjunto de todas las cadenas binarias infinitas y el conjunto de reales en\((0, 1)\) realmente son equinúmeros. (Por si te quedaba alguna duda.)
Es fácil soñar una función de inyección de\((0, 1)\) a\(\mathbb{F}^∞_2\): simplemente envíe un número real a su expansión binaria, y si hay dos, haga una elección consistente —digamos que tomaremos la expansión no terminante.
Hay un lindo pensamiento-experimento llamado Hilbert's Hotel que nos llevará a una técnica para desarrollar una función de inyección en la otra dirección. Hilbert's Hotel cuenta\(ℵ_0\) con habitaciones. Si alguna colección contable de invitados aparece habrá suficientes habitaciones para todos. Supongamos que llega al hotel de Hilbert una noche oscura y tormentosa y la luz “No Vacante” está encendida —ya hay un número denumerable de invitados allí— cada habitación está llena. El empleado te ve abatido considerando tus opciones, tratando de pensar en otro hotel que aún podría tener habitaciones cuando, claramente, hay una convención muy grande en la ciudad. Él sale corriendo y dice “¡Amigo mío, no tengas miedo! A pesar de que no tenemos vacantes, siempre hay espacio para una más en nuestro establecimiento”. Entra a la oficina y hace el siguiente anuncio sobre el sistema de PA. “Señoras y señores, para dar cabida a un invitado entrante, por favor desaloje su habitación y muévase a la habitación numerada una más alta. Gracias.” Hay una cantidad infinita de gruñidos, pero en breve te encuentras ocupando número de habitación\(1\).
Para desarrollar una inyección de\(\mathbb{F}^∞_2\) a\((0, 1)\) usaremos “número de habitación\(1\)” para separar las expansiones binarias que representan el mismo número real. Mueve todos los dígitos de una expansión binaria hacia abajo en uno, y haz el primer dígito\(0\) para (digamos) las expansiones de terminación y\(1\) para las no terminadoras. Ahora considere estas expansiones como números reales — todas las expansiones que antes coincidieron ahora están separadas en los intervalos\(\left(0, \dfrac{1}{2} \right)\) y\(\left(\dfrac{1}{2}, 1\right)\). Observe lo gracioso que es este mapa, ahora hay muchos, muchos, (infinitamente muchos) números reales sin preimágenes. Por ejemplo, solo un subconjunto de los números racionales en\(\left(0, \dfrac{1}{2} \right)\) tienen preimágenes. Sin embargo, el mapa es inyectable, por lo que C-B-S nos dice eso\(\mathbb{F}^∞_2\) y\((0, 1)\) son equivalentes. Hay bastantes pruebas diferentes del teorema C-B-S. El que escribió el propio Cantor se basa en el axioma de la elección. El axioma de elección fue algo polémico cuando se introdujo, pero en estos días la mayoría de los matemáticos lo usarán sin reparos. Lo que dice (esencialmente) es que es posible hacer un número infinito de elecciones. Más precisamente, dice que si tenemos un conjunto infinito que consiste en conjuntos no vacíos, es posible seleccionar un elemento de cada conjunto. Si existe una regla definible para elegir dicho elemento (como es el caso, por ejemplo, cuando seleccionamos la expansión decimal no terminante cada vez que hubo una opción para definir la inyección de\((0, 1)\) a\(\mathbb{F}^∞_2\)) el axioma de elección no es necesario. Los axiomas habituales para la teoría de conjuntos fueron desarrollados por Zermelo y Frankel, por lo que es posible que escuches a la gente hablar de los axiomas ZF. Si, además, queremos permitir específicamente el axioma de elección, estamos en el sistema de axiomas ZFC. Si es posible construir una prueba para un teorema dado sin usar el axioma de elección, casi todos estarían de acuerdo en que eso es preferible. Por otro lado, una prueba del teorema C-B-S, que necesariamente debe ser capaz de lidiar con conjuntos incontables infinitos, tendrá que depender de algún tipo de noción que nos permita lidiar con infinidades enormes.
La prueba que presentaremos aquí 2 se atribuye a Julius König. König era un contemporáneo de Cantor que fue (inicialmente) muy respetado por él. Cantor llegó a desgustarle König después de que este último presentara una conferencia bien publicitada (y finalmente equivocada) alegando que la hipótesis del continuum era falsa. Al parecer, la hipótesis del continuum era una de las ideas favoritas de Cantor, porque parece haber interpretado la conferencia de König como un ataque personal. En fin...
La prueba de König de C-B-S no usa el axioma de elección, pero sí tiene su propia extrañeza: una función que no es necesariamente computable, es decir, una función para la cual (para ciertas entradas) puede no ser posible calcular una salida en una cantidad finita de tiempo! Excepto por esta rareza, la prueba de König es probablemente la más fácil de entender de todas las pruebas de C-B-S. Antes de llegar demasiado lejos en la prueba es esencial que entendamos la configuración básica. El teorema de Cantor-Bernstein-Schröder establece que siempre\(A\) y\(B\) son conjuntos y hay funciones inyectoras\(f : A \implies B\) y\(g : B \implies A\), entonces se deduce que\(A\) y\(B\) son equivalentes. Decir\(A\) y\(B\) son equivalentes significa que podemos encontrar una función biyectiva entre ellos. Entonces, para probar C-B-S, planteamos la hipótesis de las dos inyecciones y de alguna manera debemos construir la biyección.
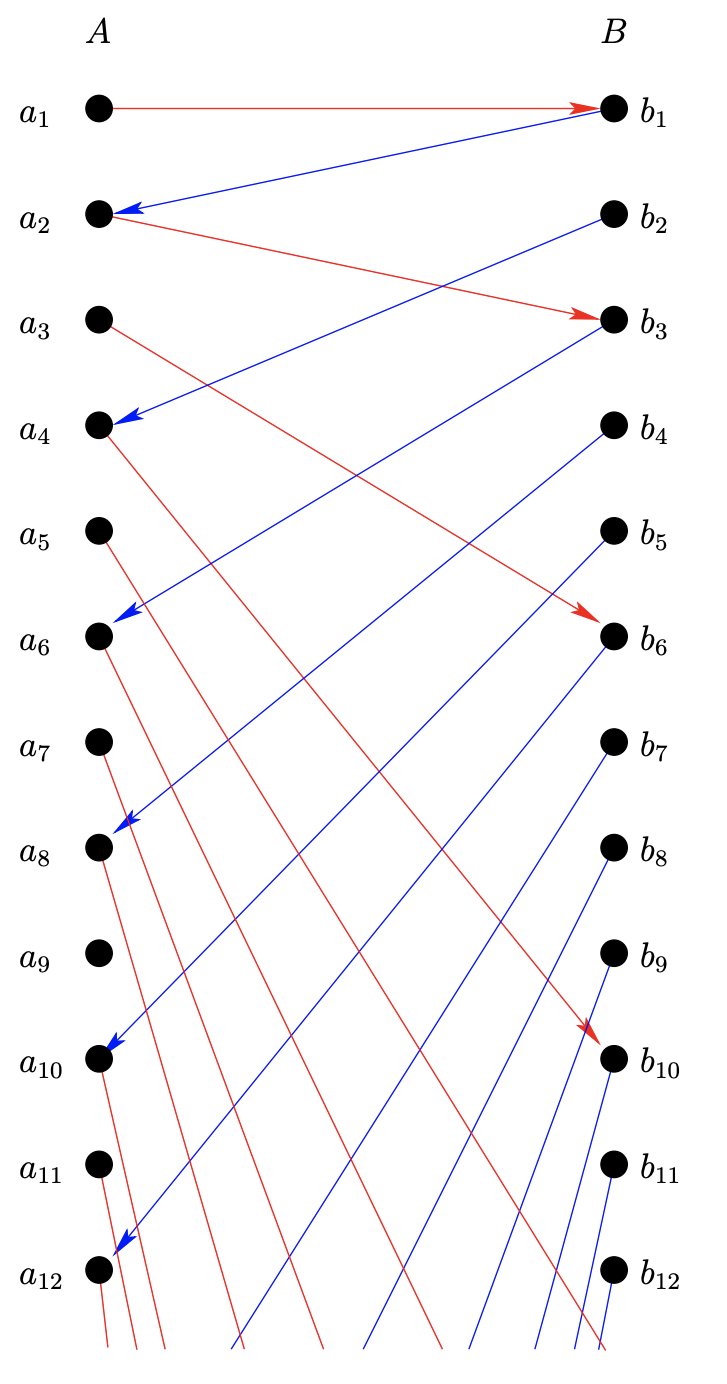
La cifra\(8.4.1.\) tiene en ella una presunción —que\(A\) y\(B\) son contables— que no tiene por qué ser el caso. Sin embargo, nos da una buena imagen para trabajar. Se muestran las hipótesis básicas, eso\(A\) y\(B\) son conjuntos y tenemos dos funciones, una de\(A\) dentro\(B\) y otra de\(B\) hacia dentro\(A\). Tendremos que construir nuestra función biyectiva de manera fragmentaria. Si hay una intersección no vacía entre\(A\) y\(B\), podemos usar la función de identidad para esa parte del dominio de nuestra bijección. Entonces, sin pérdida de generalidad, podemos presumir eso\(A\) y\(B\) somos disjuntos. Podemos usar las funciones\(f\) y\(g\) crear secuencias infinitas, que alternan de ida y vuelta entre\(A\) y\(B\), que contienen cualquier elemento en particular. Supongamos que\(a ∈ A\) es un elemento arbitrario. Ya que\(f\) se define en todos\(A\), podemos calcular\(f(a)\). Ahora ya que\(f(a)\) es un elemento de\(B\), y\(g\) se define en todos\(B\), podemos calcular\(g(f(a))\), y así sucesivamente. Así, obtenemos la secuencia infinita
\(a, f(a), g(f(a)), f(g(f(a))), . . .\)
Si el elemento\(a\) también pasa a ser la imagen de algo debajo\(g\) (esto puede o no ser así — ya que\(g\) no es necesariamente sobre) entonces también podemos extender esta secuencia hacia la izquierda. En efecto, puede ser posible extender la secuencia infinitamente hacia la izquierda, o bien, este proceso puede detenerse cuando uno de\(f^{−1}\)\(g^{−1}\) o no se define.
\(. . . g^{−1} (f^{−1} (g^{−1} (a))), f^{−1} (g^{−1} (a)), g^{−1} (a), a, f(a), g(f(a)), f(g(f(a))), . . .\)
Ahora, cada elemento de la unión disjunta de\(A\) y\(B\) está en una de estas secuencias. Además, es fácil ver que estas secuencias son o bien disjuntas o idénticas. Tomando estos dos hechos juntos se deduce que estas secuencias forman una partición de\(A ∪ B\). Definiremos una biyección\(\phi : A \implies B\) decidiendo qué debe hacer en estas secuencias. Hay cuatro posibilidades de cómo pueden funcionar las secuencias que acabamos de definir. Al extenderlas hacia la izquierda, podemos encontrarnos con un lugar donde una de las funciones inversas necesarias no esté definida —o no—. Decimos que una secuencia es un\(A\) -tope, si, al extenderse hacia la izquierda, terminamos sobre un elemento de\(A\) que no tiene preimagen debajo\(g\) (ver Figura\(8.4.2\)). De igual manera, podemos definir un\(B\) -tapón. Si las funciones inversas siempre se definen dentro de una secuencia dada también hay dos posibilidades; la secuencia puede ser finita (y por lo tanto debe ser de naturaleza cíclica) o la secuencia puede ser verdaderamente infinita.
Por último, aquí hay una definición para\(\phi\).
\( \phi(x)=\left\{ \begin{array}{ll} g^{−1}(x) \;\;\;\;\text{ if } x \text{ is in a } B\text{-stopper}\\ f(x) \;\;\;\;\;\;\;\text{ otherwise} \end{array} \right.\)
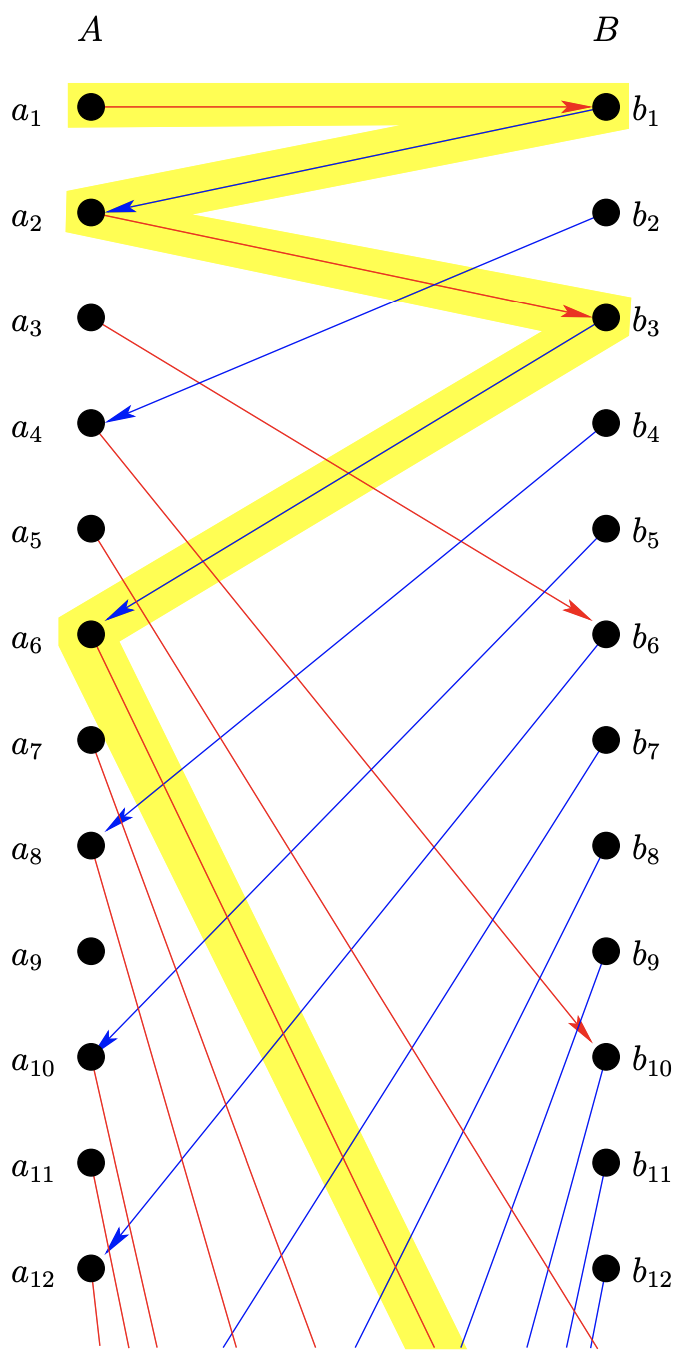
Observe que si una secuencia es cíclica o infinita no importa si usamos\(f\) o\(g^{−1}\) ya que ambas se definirán para todos los elementos de tales secuencias. También, sin duda\(f\) va a funcionar si estamos en un\(A\) -tapón. La función que acabamos de crear está perfectamente bien definida, pero puede tomar arbitrariamente mucho tiempo determinar si tenemos un elemento de un\(B\) -stopper, a diferencia de un elemento de una secuencia infinita. No podemos determinar si estamos en una secuencia infinita versus una finita en un número finito prescrito de pasos.
Ejercicios:
¿Cómo podría el empleado del Hotel Hilbert dar cabida a un número contable de nuevos huéspedes?
Dejar\(F\) ser la colección de todas las funciones de valor real definidas en la línea real. Encuentra una inyección de\(\mathbb{R}\) a\(F\). ¿Crees que es posible encontrar una inyección yendo por el otro lado? Es decir, ¿piensas eso\(F\) y\(\mathbb{R}\) son equivalentes? Explicar.
Rellene los datos de la prueba de que el dominio es una relación ordenadora. (Simplemente puede citar el teorema C-B-S para probar la antisimetría).
Podemos\(\mathbb{Q}\) inyectar en\(\mathbb{Z}\) enviando\(± \dfrac{a}{b}\) a\(±2^a 3^b\). Utilice esta y otra inyección obvia para (a la luz del teorema C-B-S) reafirmar la equivalencia de estos conjuntos.


