1.6: Secuencias
- Page ID
- 118493
En el cálculo pensamos en una secuencia como una lista (posiblemente infinita) de objetos. Ampliaremos un poco esa idea, y la expresaremos en el lenguaje de las funciones.
Una secuencia finita es una función\(f\) con dominio\(\ulcorner N\urcorner\), donde\(N \in \mathbb{N}\). A menudo identificamos la secuencia con el conjunto finito ordenado\(\left\langle a_{n} \mid n<N\right\rangle\), donde\(a_{n}=f(n)\), para\(0 \leq n<N\).
Esta interpretación de una secuencia como un tipo de función se extiende fácilmente a secuencias infinitas.
Una secuencia infinita es una función\(f\) con dominio\(\mathbb{N}\). A menudo identificamos la secuencia con el conjunto infinito ordenado\(\left\langle a_{n} \mid n \in \mathbb{N}\right\rangle\), donde\(a_{n}=f(n)\), para\(n \in \mathbb{N}\).
OBSERVACIÓN. Intervalo en\(\mathbb{Z}\) Realmente, la secuencia de palabras se usa normalmente para significar cualquier función cuyo dominio sea un intervalo in\(\mathbb{Z}\), donde un intervalo in\(\mathbb{Z}\) es la intersección de algún intervalo real con\(\mathbb{Z}\). Por conveniencia en este libro, solemos suponer que el primer elemento de cualquier secuencia está indexado por 0 o 1.
La secuencia\(\langle 0,1,4,9, \ldots\rangle\) viene dada por la función\(f(n)=n^{2} .\)
La secuencia\(\langle 1,-1,2,-2,3,-3, \ldots\rangle\) viene dada por la función\[f(n)= \begin{cases}\frac{n}{2}+1, & n \text { even } \\ -\frac{n+1}{2}, & n \text { odd. }\end{cases}\] Secuencias puede tomar valores en cualquier conjunto (el codominio de la función\(f\) que define la secuencia). Hablamos de una secuencia real si los valores son números reales, una secuencia entera si todos son enteros, etc. resultará más tarde que las secuencias con valores en el conjunto de dos elementos\(\{0,1\}\) ocurren con bastante frecuencia, así que tenemos un nombre especial para ellos: los llamamos secuencias binarias.
Una secuencia binaria finita es una función,\(f:\ulcorner N\urcorner \rightarrow\ulcorner 2\urcorner\), para algunos\(N \in \mathbb{N}\). Una secuencia binaria infinita es una función,\(f: \mathbb{N} \rightarrow\ulcorner 2\urcorner\).
A menudo usamos la expresión\(\left\langle a_{n}\right\rangle\) para la secuencia\(\left\langle a_{n} \mid n \in \mathbb{N}\right\rangle\).
Las funciones también se utilizan para “indexar” conjuntos con el fin de construir conjuntos más complicados con operaciones de conjunto generalizadas. Se discutió la unión (o intersección) de más de dos conjuntos. Podría preguntarse si es posible formar uniones o intersecciones de una gran colección (infinita) de conjuntos. Hay dos preocupaciones que deben abordarse al responder a esta pregunta. Debemos estar seguros de que la definición de la unión de infinitamente muchos conjuntos es precisa; es decir, caracteriza de manera única a un objeto en el universo matemático. También necesitamos notación para manejar esta idea - ¿cómo especificamos los conjuntos sobre los que estamos tomando el sindicato?
Para\(n \in \mathbb{N}^{+}\), deja\(X_{n}\) ser un conjunto. Entonces\[\bigcup_{n=1}^{\infty} X_{n}=\left\{x \mid \text { for some } n \in \mathbb{N}^{+}, x \in X_{n}\right\} \text {. }\] El conjunto\(\mathbb{N}^{+}\) se llama el conjunto de índices para la unión.
Esto puede escribirse de algunas maneras diferentes.
NOTACIÓN. \(\bigcup_{n \in \mathbb{N}^{+}} X_{n}\)Las siguientes tres expresiones son todas iguales:
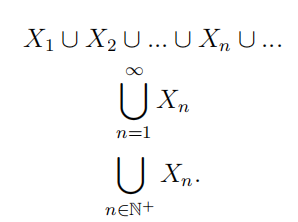
Podemos usar conjuntos de índices distintos a\(\mathbb{N}^{+}\).
Dejar\(A\) ser un conjunto, y para\(\alpha \in A\), dejar\(X_{\alpha}\) ser un conjunto. El conjunto\[\mathcal{F}=\left\{X_{\alpha} \mid \alpha \in A\right\}\] se llama familia de conjuntos indexados por\(A\). Entonces\(\bigcup_{\alpha \in A} X_{\alpha}\) Se lee\[\bigcup_{\alpha \in A} X_{\alpha}=\left\{x \mid x \in X_{\alpha} \text { for some } \alpha \in A\right\} \text {. }\] la notación “la unión sobre alfa en A de los conjuntos X sub alfa”. Entonces las intersecciones\[x \in \bigcup_{\alpha \in A} X_{\alpha} \text { if } x \in X_{\alpha} \text { for some } \alpha \in A \text {. }\] generales sobre una familia de conjuntos se definen análogamente:\[\bigcap_{\alpha \in A} X_{\alpha}=\left\{x \mid x \in X_{\alpha} \text { for all } \alpha \in A\right\} .\] EJEMPLO 1.43. Dejar\(X_{n}=\{n+1, n+2, \ldots, 2 n\}\) para cada uno\(n \in \mathbb{N}^{+}\). Entonces\[\begin{aligned} &\bigcup_{n=1}^{\infty} X_{n}=\{k \in \mathbb{N} \mid k \geq 2\} \\ &\bigcap_{n=1}^{\infty} X_{n}=\emptyset . \end{aligned}\] Ejemplo 1.44. Por cada número real positivo\(t\), vamos\(Y_{t}=[11 / t, t]\). Entonces\[\begin{aligned} \bigcup_{t \in(\sqrt{11}, \infty)} Y_{t} &=\mathbb{R}^{+} \\ \bigcap_{t \in[\sqrt{11}, \infty)} Y_{t} &=\{\sqrt{11}\} . \end{aligned}\] EJEMPLO 1.45. Dejar\(f: X \rightarrow Y, A \subseteq X\) y\(B \subseteq Y\). Entonces\[\bigcup_{a \in A}\{f(a)\}=f[A] .\] y\[\bigcup_{b \in B} f^{-1}(b)=f^{-1}[B] .\]


