1.5: Imágenes e inversos
- Page ID
- 118486
Las funciones se pueden utilizar para definir subconjuntos de conjuntos dados.
Dejar\(f: X \rightarrow Y\) y\(W \subseteq X\). La imagen de\(W\) debajo\(f\), escrita\(f[W]\), es el conjunto\[\{f(x) \mid x \in W\} .\] Así que si\(f: X \rightarrow Y\), entonces\[\operatorname{Ran}(f)=f[X] .\] EJEMPLO 1.30. Supongamos que\(f\) es la función real\(f(x)=x^{2}+3\). Vamos\(W=\{-2,2,3\}\), y\(Z=(-1,2)\). Entonces\(f[W]=\{7,12\}\), y\(f[Z]=[3,7)\).
En aplicaciones de las matemáticas, las funciones suelen describir relaciones numéricas entre observaciones medibles. Entonces si\(f: X \rightarrow Y\) y\(a \in X\), entonces\(f(a)\) es la medida predicha o real asociada con\(a\). En este contexto, a menudo uno está interesado en determinar qué elementos de\(X\) están asociados a un valor,\(b\), en el codominio de\(f\).
Dejar\(f: X \rightarrow Y\) y\(b \in Y\). Entonces la imagen inversa de\(b\) under\(f, f^{-1}(b)\), es el conjunto\[\{x \in X \mid f(x)=b\} .\] Este conjunto también se llama la pre-imagen de\(b\) under\(f\).
Tenga en cuenta que si\(b \notin \operatorname{Ran}(f)\), entonces\(f^{-1}(b)=\emptyset\). Si\(f\) es una inyección, entonces para cualquiera\(b \in \operatorname{Ran}(f), f^{-1}(b)\) tiene un solo elemento.
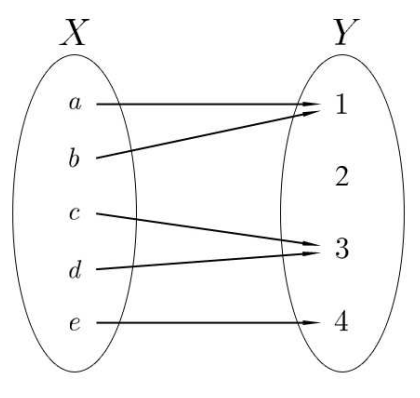
Dejar\(f: X \rightarrow Y\) y\(Z \subseteq Y\). La imagen inversa de\(Z\) under\(f\), o la pre-imagen de\(Z\) under\(f\), es el conjunto\[f^{-1}[Z]=\{x \in X \quad \mid f(x) \in Z\}\] que usamos\(f^{-1}[]\) para significar la imagen inversa de un subconjunto del codominio, y\(f^{-1}\) () para la imagen inversa de un elemento del codominio - ambos son subconjuntos del dominio de\(f\). Si\(Z \cap \operatorname{Ran}(f)=\emptyset\), entonces\[f^{-1}[Z]=\emptyset .\] EJEMPLO 1.32. \(f\)Sea como en Figura\(1.33\) Entonces\(f[\{b, c\}]=\{1,3\}\), y\(f^{-1}[\{1,3\}]=\{a, b, c, d\}\).
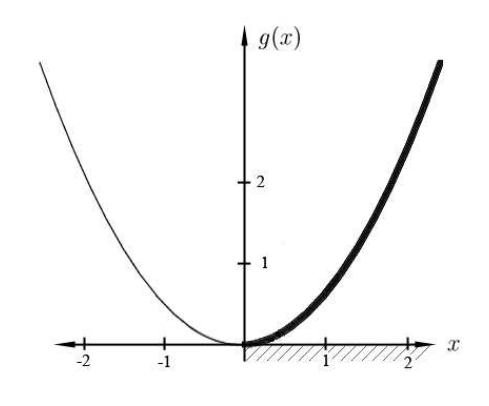
\(g\)Déjese ser la verdadera función\(g(x)=x^{2}+3\). Si\(b \in \mathbb{R}\) y\(b>3\), entonces\[g^{-1}(b)=\{\sqrt{b-3},-\sqrt{b-3}\} .\] Si\(b=3\), entonces\(g^{-1}(3)=\{0\}\). Si\(b<3\), entonces\(g^{-1}(b)\) está vacío.
\(h\)Déjese ser la verdadera función\(h(x)=e^{x}\). Si\(b \in \mathbb{R}\) y\(b>0\), entonces\[h^{-1}(b)=\left\{\log _{e}(b)\right\} .\] Por ejemplo,\[h^{-1}(1)=\{0\} .\] Porque\(h\) es estrictamente creciente, la imagen inversa de cualquier elemento del codominio\((\mathbb{R})\) es o bien un conjunto con un solo elemento o el conjunto vacío.
Let\(I=(a, b)\), donde\(a, b \in \mathbb{R}\) y\(0<a<b\) (\(I\)es decir, el intervalo abierto con puntos finales\(a\) y\(b\)). Luego\[h^{-1}[I]=\left(\log _{e}(a), \log _{e}(b)\right) .\] hemos discutido la construcción de nuevas funciones a partir de funciones existentes utilizando operaciones algebraicas y composición de funciones. Otra herramienta para construir nuevas funciones a partir de funciones conocidas es la función inversa.
\(f: X \mapsto Y\)Déjese ser una biyección. Entonces la función inversa de\(f, f^{-1}: Y \rightarrow X\), es la función con gráfica\[\{(b, a) \in Y \times X \mid(a, b) \in \operatorname{graph}(f)\} .\] La función\(f^{-1}\) se define por “revertir las flechas”. Para que esto tenga sentido,\(f: X \rightarrow Y\) debe ser biyectiva. En efecto, si no\(f\) fueran suryectivas, entonces habría un elemento\(y\) de\(Y\) que no está en el rango de\(f\), por lo que no se puede mapear de nuevo a nada en\(X\). Si no\(f\) fueran inyectables, habría elementos\(z\) de\(Y\) que fueran la imagen de elementos distintos\(x_{1}\) y\(x_{2}\) en\(X\). No se podría definir\(f^{-1}(z)\) sin especificar cómo elegir una preimagen en particular. Ambos problemas pueden ser solucionados. Si\(f\) es inyectable pero no suryectiva, se puede definir\(g: X \mapsto \operatorname{Ran}(f)\) por\[g(x)=f(x)\] para todos\(x \in X\). Entonces\(g^{-1}: \operatorname{Ran}(f) \mapsto X\). Si no\(f\) es inyectable, el problema es más difícil; pero si podemos encontrar algún subconjunto\(X\) sobre el cual\(f\) es inyectable, podríamos restringir nuestra atención a ese conjunto.
\(f\)Déjese ser la verdadera función\(f(x)=x^{2}\). La función no\(f\) es una biyección, por lo que no tiene una función inversa. Sin embargo, la función\[\begin{aligned} g:[0, \infty) & \rightarrow[0, \infty) \\ x & \mapsto x^{2} \end{aligned}\] es una biyección. En este caso,\[g^{-1}(y)=\sqrt{y} .\]
Que\(f\) sea la verdadera función,\(f(x)=e^{x}\). Sabes por cálculo que\(f\) es una inyección, y eso\(\operatorname{Ran}(f)=\mathbb{R}^{+}\). De ahí\(f\) que no sea una sobreyección, ya que el codominio implícito de una función real lo es\(\mathbb{R}\). La función\[\begin{aligned} g: \mathbb{R} & \rightarrow \mathbb{R}^{+} \\ x & \mapsto e^{x} \end{aligned}\] es una biyección y\[g^{-1}(x)=\log _{e}(x)\] Advertencia: Para\(f: X \mapsto Y\) una biyección hemos asignado dos significados diferentes a\(f^{-1}(b)\). En la Definición 1.31, significa el conjunto de puntos en los\(X\) que se mapean\(b\). En la Definición 1.36, significa la función inversa\(f^{-1}\),, de la biyección\(f\) aplicada al punto\(b \in Y\). Sin embargo, si\(f\) es una biyección, para que la segunda definición tenga sentido, entonces estas definiciones están estrechamente relacionadas. Supongamos\(a \in \operatorname{Dom}(f)\) y\(f(a)=b\). De acuerdo con la Definición 1.31,\(f^{-1}(b)=\{a\}\) y por Definición\(1.36\)\(f^{-1}(b)=a\). En la práctica el contexto dejará claro qué definición se pretende. DEFINICIÓN. Función de identidad, id\(\left.\right|_{X}\) Let\(X\) be a set. La función de identidad on\(X\), id\(\left.\right|_{X}: X \mapsto X\), es la función definida por\[\left.\operatorname{id}\right|_{X}(x)=x .\] If\(f: X \rightarrow Y\) es una biyección, entonces\(f^{-1}\) es la función única tal que\[f^{-1} \circ f=\left.\operatorname{id}\right|_{X}\] y\[f \circ f^{-1}=\left.\mathrm{id}\right|_{Y} .\] Porque \(f(x)=x^{2}\)no es una inyección, no tiene inversa, incluso después de restringir el codominio para que sea el rango. Por lo tanto, para “invertir”\(f\), consideramos una función diferente\(g(x)\), que era igual a\(f\) sobre un subconjunto del dominio de\(f\), y era una inyección. En el Ejemplo 1.37, logramos esto definiendo la función\(g(x)=x^{2}\) con dominio\(\{x \in \mathbb{R} \mid x \geq 0\}\). Muchas de las funciones que necesitamos invertir por razones prácticas y teóricas pasan no ser inyecciones, y por lo tanto no tienen funciones inversas. Una forma de abordar este obstáculo es considerar la función en un dominio más pequeño.
Dada una función, es posible\(f: X \rightarrow Y\) que deseemos definir una “inversa” de\(f\) en algún subconjunto\(W \subseteq X\) para el cual la restricción de\(f\) a\(W\) es una inyección.
Dejar\(f: X \rightarrow Y\) y\(W \subseteq X\). La restricción de\(f\) a\(W\), escrito\(\left.f\right|_{W}\), es la función\[\begin{aligned} \left.f\right|_{W}: W & \rightarrow Y \\ x & \mapsto f(x) . \end{aligned}\] Así que si\(f: X \rightarrow Y\) y\(W \subseteq X\), entonces\[\operatorname{graph}\left(\left.f\right|_{W}\right)=[W \times Y] \cap[\operatorname{graph}(f)] .\] EJEMPLO 1.40. Vamos\(f(x)=(x-2)^{4}\). Vamos\(W=[2, \infty)\). Entonces\[\left.f\right|_{W}: W \rightarrow[0, \infty)\] es una biyección. EJEMPLO 1.41. Que\(f\) sea la verdadera función,\(f(x)=\tan (x)\). Entonces\[\operatorname{Dom}(f)=\{x \in \mathbb{R} \mid x \neq \pi / 2+k \pi, k \in \mathbb{Z}\},\] y\[\operatorname{Ran}(f)=\mathbb{R} .\] La función\(f\) es periódica con periodo\(\pi\), y por lo tanto no es una inyección. No obstante, es importante responder a la pregunta, “En qué ángulo (s),\(x\), hace\(\tan (x)\) igual a un valor particular\(a \in \mathbb{R}\)”.
Esto es matemáticamente equivalente a preguntar,\[\text { "What is } \arctan (a) \text { ?". }\] En cálculo esta necesidad se satisfizo restringiendo el dominio a un intervalo mayor,\(I\) tal que\[\left.f\right|_{I}: I \mapsto \mathbb{R}\] Para cualquiera\(k \in \mathbb{Z}\),\[\left(\frac{(2 k+1) \pi}{2}, \frac{(2 k+3) \pi}{2}\right)\] es tal intervalo. Para definir una función específica, se selecciona el más simple de estos intervalos, y definimos\[\operatorname{Tan}:=\left.\tan \right|_{(-\pi / 2, \pi / 2)} .\] Observar que\[\text { Tan : }(-\pi / 2, \pi / 2) \mapsto \mathbb{R} .\] Así la función es invertible, es decir, Tan tiene una función inversa,\[\operatorname{Arctan}=\operatorname{Tan}^{-1} \text {. }\]


