2.2: Pedidos
- Page ID
- 118523
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Una relación en un conjunto puede pensarse como parte de la estructura impuesta al conjunto. Entre las relaciones más importantes en un conjunto están las relaciones de orden.
\(X\)Sea un conjunto y\(R\) una relación sobre\(X\). Decimos que\(R\) es un ordenamiento parcial si:
(1)\(R\) es reflexivo
(2)\(R\) es antisimétrico
(3)\(R\) es transitivo.
\(X\)Déjese ser una familia de conjuntos. La relación\(\subseteq\) es un ordenamiento parcial sobre\(X\). Cada conjunto es un subconjunto de sí mismo, por lo que la relación es reflexiva. Si\(Y \subseteq Z\) y\(Z \subseteq Y\), entonces\(Y=Z\), entonces la relación es antisimétrica. Por último, si\(Y \subseteq Z\) y\(Z \subseteq W\) entonces\(Y \subseteq W\), entonces la relación es transitiva.
\(R\)Sea la relación sobre\(\mathbb{N}^{+}\) definida por\(x R y\) si y sólo si hay\(z \in \mathbb{N}^{+}\) tal que\[x z=y .\] Entonces\(R\) es un ordenamiento parcial de\(\mathbb{N}^{+}\). (Demostrar esto: Ejercicio 2.2).
Dejar\(X\) ser un conjunto y\(R\) ser un orden parcial de\(X\). Decimos que\(R\) es un ordenamiento lineal, también llamado ordenamiento total, siempre que, para cualquiera\(x, y \in X\), ya sea\(x R y\) o\(y R x\).
Tenga en cuenta que dado que un orden lineal es antisimétrico, para cualquier distinto\(x\) y\(y\), exactamente uno de\(x R y\) y\(y R x\) mantiene.
El orden\(\leq\) en\(\mathbb{N}\) (o\(\mathbb{R}\)) es un orden lineal. Así es la relación\(\geq\). La relación no\(<\) es (¿por qué?).
Vamos\(X=\mathbb{R}^{n}\). Podemos definir una relación reflexiva de la\(X\) siguiente manera. Dejar\(x=\left(a_{1}, \ldots, a_{n}\right)\) y\(y=\left(b_{1}, \ldots, b_{n}\right)\) ser miembros distintos de\(X\). Que\(k \in \mathbb{N}^{+}\) sea el menor número tal que\(a_{k} \neq b_{k}\). Entonces definimos\[x R y \text { if and only if } a_{k}<b_{k} .\] Entonces\(R\) es un ordenamiento lineal de\(X\). Se llama el orden del diccionario.
La noción de un ordenamiento lineal es probablemente natural para ti, y la has usado intuitivamente desde que empezaste a estudiar aritmética. La relación\(\leq\) ayuda a visualizar el conjunto como una línea en la que la ubicación relativa de dos elementos del conjunto está determinada por el orden lineal. Si está considerando un conjunto con operaciones, esto a su vez puede ayudar a visualizar cómo se comportan las operaciones. Por ejemplo, piense en usar una recta numérica para visualizar suma, resta y multiplicación de enteros.
Los ordenamientos parciales son generalizaciones de ordenamientos lineales, y\(\leq\) es el ejemplo más obvio de un ordenamiento lineal. Debido a esto, el símbolo normal para un ordenamiento parcial es\(\preceq\) (también recuerda al símbolo\(\subseteq\), que es el ejemplo que la mayoría de los matemáticos tienen en cuenta al pensar en un ordenamiento parcial).
Deja\(X\) ser el conjunto de todas las colecciones de manzanas y naranjas. Si\(x, y\) están en\(X\), entonces diga\(x \preceq y\) si el número de manzanas en\(x\) es menor o igual que el número de manzanas en\(y\), y el número de naranjas en\(x\) es menor o igual que el número de naranjas en\(y\). Se trata de un ordenamiento parcial. Puede que no puedas comparar manzanas con naranjas, pero puedes decir que ¡2 manzanas y 5 naranjas es inferior a 4 manzanas y 6 naranjas!
Una forma de visualizar un orden parcial\(\preceq\) en un conjunto finito\(X\) es imaginar flechas que conectan elementos distintos de\(X, x\) y\(y\), si\(x \preceq y\) y no hay un tercer punto distinto que\(z\) satisfaga \(x \preceq z \preceq y\). Entonces dos elementos\(a\) y\(b\) en\(X\) satisfarán\(a \preceq b\) si y sólo si se puede llegar de\(a\) a\(b\) siguiendo un camino de flechas.
Considera la gráfica en el conjunto\(X=\{a, b, c, d, e, f\}\) dan en la Figura 2.11.
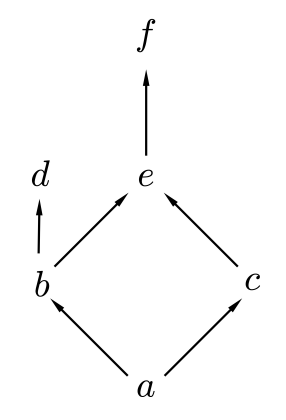
Ilustra el orden parcial que podría describirse como la relación reflexiva, transitiva más pequeña\(\preceq\) sobre la\(X\) que satisface\(a \preceq b, a \preceq c, b \preceq\)\(d, b \preceq e, c \preceq e, e \preceq f .\)


