9.1: Cubicos
- Page ID
- 118494
¿Cómo se encuentran las raíces de un polinomio cúbico? Los babilonios conocían la fórmula cuadrática en el segundo milenio antes de Cristo, pero una fórmula para el cúbico solo se encontró en el\(16^{\text {th }}\) siglo. La historia del descubrimiento es complicada, pero la mayor parte del crédito debería ir a Nicolo Tartaglia. La solución fue publicada en 1545 en el influyente libro Artis magnae sive de regulis algebraicis liber unus de Girolomo Cardano. \(9.2\)La fórmula se conoce hoy como la fórmula Tartaglia-Cardano. Para un relato histórico, véase por ejemplo [6].
Considerar un polinomio cúbico en\(\mathbb{R}[x]\)\[p(x)=a_{3} x^{3}+a_{2} x^{2}+a_{1} x+a_{0} .\] Si queremos encontrar las raíces, no hay pérdida de generalidad al asumir que\(a_{3}=1\), ya que los ceros de\(p\) son los mismos que los ceros de\(\frac{1}{a_{3}} p\).
La segunda simplificación es que podemos asumir\(a_{2}=0\). Efectivamente, hacer el cambio de variable\[x=y-\beta,\] para\(\beta\) que algunos sean elegidos posteriormente. Entonces\[\begin{aligned} p(x) &=x^{3}+a_{2} x^{2}+a_{1} x+a_{0} \\ &=(y-\beta)^{3}+a_{2}(y-\beta)^{2}+a_{1}(y-\beta)+a_{0} \\ &=y^{3}+\left[a_{2}-3 \beta\right] y^{2}+\left[a_{1}-2 a_{2} \beta+3 \beta^{2}\right] y+\left[a_{0}-a_{1} \beta+a_{2} \beta^{2}-\beta^{3}\right] \\ &=: \quad q(y) . \end{aligned}\] elige\(\beta=a_{2} / 3\). Entonces el coeficiente de\(y^{2}\) in se\(q(y)\) desvanece. Supongamos que puedes encontrar las raíces de\(q\), llámalos\(\alpha_{1}, \alpha_{2}, \alpha_{3}\). Entonces\(p\) son las raíces del polinomio original\(\alpha_{1}-\beta, \alpha_{2}-\beta, \alpha_{3}-\beta\).
Por lo tanto, basta con encontrar una fórmula para las raíces de un cúbico en el que el término cuadrático se desvanece. Esto se llama cúbico reducido. Como ahora solo quedan dos coeficientes, bajaremos los subíndices y escribiremos nuestro cúbico reducido como\[q(x)=x^{3}+a x+b .\] La idea clave es hacer otra sustitución, más ingeniosa. Introduzcamos una nueva variable\(w\), relacionada con\(x\) por\[x=w+\frac{c}{w},\] donde\(c\) es una constante que elegiremos más adelante. \[c=-\frac{a}{3},\]Entonces\[\begin{aligned} q(x) &=\left(w+\frac{c}{w}\right)^{3}+a\left(w+\frac{c}{w}\right)+b \\ &=w^{3}+[3 c+a] w+\left[3 c^{2}+a c\right] \frac{1}{w}+c^{3} \frac{1}{w^{3}}+b . \end{aligned}\] Elige para que tanto el coeficiente\(w\) de como\(1 / w\) en (9.4) desaparezca. \(x\)Entonces encontrar así que\(q(x)=0\) es lo mismo que encontrar\(w\) para que la\[\begin{aligned} w^{3}+\frac{c^{3}}{w^{3}}+b &=0 \\ \Longleftrightarrow w^{6}+b w^{3}+c^{3} &=0 . \end{aligned}\] Ecuación (9.5) sea de grado 6, lo que parece peor que el cúbico original; pero desaparecen tantos términos que en realidad es una ecuación cuadrática en \(w^{3}\). Por lo tanto se puede resolver por la fórmula cuadrática:\[w^{3}=\frac{-b \pm \sqrt{b^{2}-4 c^{3}}}{2} .\] Sabiendo\(w\), podemos recuperarnos\(x\) por\[x=w+\frac{c}{w}=w-\frac{a}{3 w} .\] Así llegamos a la fórmula Tartaglia-Cardano para las raíces del cúbico reducido (9.2):\[x=\left[\frac{-b \pm \sqrt{b^{2}+\frac{4 a^{3}}{27}}}{2}\right]^{1 / 3}-\frac{a}{3\left[\frac{-b \pm \sqrt{b^{2}+\frac{4 a^{3}}{27}}}{2}\right]^{1 / 3}} .\] ¿Cómo funciona el trabajo de fórmula en la práctica?
EJEMPLO 9.8. Vamos\(p(x)=x^{3}-3 x+2\). Entonces\(c=1\), y (9.6) dice\(w^{3}=-1\). Por lo tanto\(w=-1\), y así\(x=-2\) es una raíz. Por lo tanto, por Lemma\(4.13,(x+2)\) es un factor de\(p\). Factorización, obtenemos\[x^{3}-3 x+2=(x+2)\left(x^{2}-2 x+1\right) .\] El último término factores como\((x-1)^{2}\), por lo que concluimos que las raíces son\(-2,1,1\).
En el Ejemplo 9.8, la fórmula funcionó, pero sólo nos dio una de las raíces. Considera el siguiente ejemplo:
EJEMPLO 9.9. Vamos\[p(x)=x^{3}-3 x+1 .\] Entonces\(c=1\), y\[w^{3}=\frac{-1 \pm \sqrt{-3}}{2} .\] Ahora tenemos un problema peor:\(w^{3}\) implica la raíz cuadrada de un número negativo, y aunque le demos sentido a eso, entonces tenemos que extraer una raíz cúbica. Es esto analago a tratar de resolver la ecuación cuadrática\[q(x):=x^{2}+x+1=0 ?\] La fórmula cuadrática vuelve a dar el lado derecho de\((9.11)\), y lo explicamos diciendo que de hecho no\(q\) tiene raíces reales. En efecto, la gráfica muestra que\(q\) se parece a la Figura 9.12.
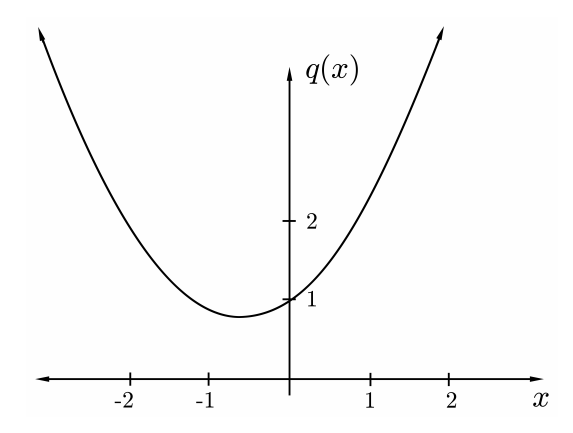
Pero esto no puede ser el caso\(p\). En efecto, por\[\begin{aligned} p(-2) &=-1<0 \\ p(0) &=1>0 \\ p(1) &=-1<0 \\ p(2) &=3>0 \end{aligned}\] lo tanto, por el Teorema del Valor Intermedio\(8.10, p\) debe tener una raíz en cada uno de los intervalos\((-2,0),(0,1)\) y\((1,2)\). Como\(p\) puede tener como máximo 3 raíces por Teorema\(4.10\), por lo tanto, debe tener exactamente tres raíces. Una gráfica de\(p\) se parece a la Figura 9.13.
Resulta que se pueden encontrar las raíces de\(p\) en Ejemplo\(9.9\) interpretando correctamente la fórmula Tartaglia-Cardano. Volveremos a este ejemplo en la Sección 9.3, después de que desarrollemos las ideas necesarias. La gran idea es introducir la noción de un número complejo.


