9.2: Números Complejos
- Page ID
- 118492
DEFINICIÓN. Número complejo Un número complejo es una expresión de la forma\(a+i b\), donde\(a\) y\(b\) son números reales.
Por el momento, se puede pensar\(i\) en el in\(a+i b\) como un símbolo formal, o un lugaretero. Posteriormente, veremos que tiene otra interpretación.
Notación. \(\mathbb{C}\)Vamos a dejar\(\mathbb{C}\) denotar el conjunto de todos los números complejos:\[\mathbb{C}=\{a+i b: a, b \in \mathbb{R}\} .\] Como conjunto, uno puede identificarse\(\mathbb{C}\) con de la\(\mathbb{R}^{2}\) manera obvia. Esto nos permite definir la suma; lo que no es tan obvio es que también hay una buena definición para la multiplicación.
DEFINICIÓN. Dejar\(a+i b\) y\(c+i d\) ser números complejos. Entonces su suma y producto se definen por\[\begin{aligned} (a+i b)+(c+i d) &=(a+c)+i(b+d) \\ (a+i b) \times(c+i d) &=(a c-b d)+i(a d+b c) . \end{aligned}\] La fórmula para la suma (9.14) es justo lo que obtendrías si identificaras el número complejo\(a+i b\) con el vector\((a, b)\) en\(\mathbb{R}^{2}\) y usaras la adición de vector. El producto es más sutil. Si multiplicas el lado izquierdo de (9.15), obtienes\[a c+i(a d+b c)+i^{2} b d .\] Uno llega al lado derecho de (9.15) definiendo\[i^{2}=-1 \text {. }\] Así\(i\) es la raíz cuadrada de\(-1\); es decir, es una cantidad algebraica que introducimos que se define a tener la propiedad que es su plaza\(-1\). Obviamente esto\(i\) impide ser un número real.
En esencia hemos continuado el programa de definición de sistemas numéricos que iniciamos en el Capítulo 8. La suma y multiplicación de números complejos se han definido por operaciones algebraicas sobre\(\mathbb{R} \times \mathbb{R}\). Dado que las operaciones algebraicas sobre los números reales se definieron teóricamente en conjunto, hemos definido operaciones algebraicas en operaciones\(\mathbb{C}\) por conjunto. A diferencia de los otros sistemas de números que hemos definido, no definimos un orden lineal de\(\mathbb{C}\). Generalmente no es útil pensar en números complejos en una recta numérica. Sin embargo, es muy útil pensar en los números complejos como puntos en el plano\(\mathbb{R}^{2}\), y describirlos en coordenadas polares.
Como es habitual, el punto con coordenadas cartesianas\((x, y)\) tiene coordenadas polares\((r, \theta)\), donde están relacionadas por\[\begin{array}{cl} r=\sqrt{x^{2}+y^{2}} & \tan (\theta)=y / x \\ x=r \cos \theta & y=r \sin \theta . \end{array}\] Así que el número complejo también se\(z=x+i y\) puede escribir como\[z=r(\cos \theta+i \sin \theta) .\] La forma (9.18) es tan ampliamente utilizada que hay una notación especial para ello.
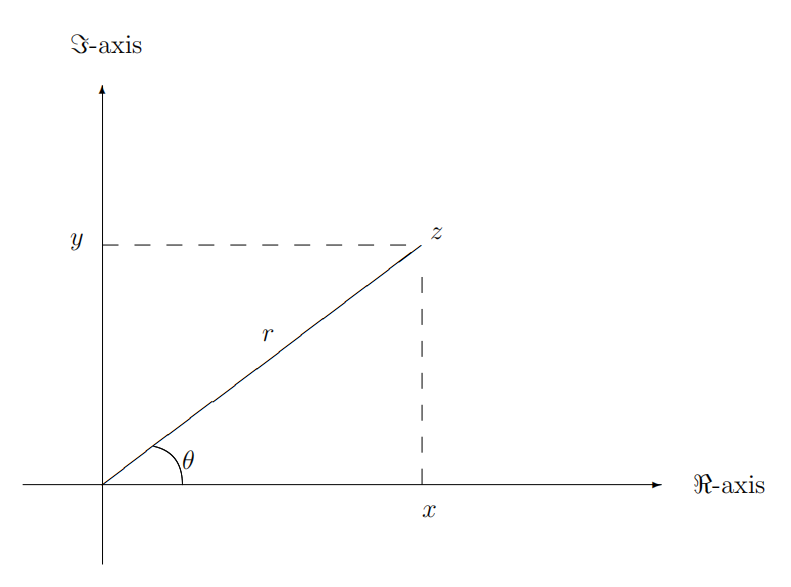
Notación. \[\operatorname{Cis}(\theta):=\cos \theta+i \sin \theta .\]DEFINICIÓN CIS. Para el número complejo\(z=x+i y=r \operatorname{Cis}(\theta)\), tenemos lo siguiente:
\(\Re(z) x\)se llama la parte real de\(z\), escrito\(\Re(z)\);
\(\Im(z) y\)se llama la parte imaginaria de\(z\), escrito\(\Im(z)\);
\(|z| r\)se llama el módulo de\(z\), o valor absoluto de\(z\), escrito\(|z|\);\(\arg (z) \theta\) se llama el argumento de\(z\), escrito\(\arg (z)\).
\(\bar{z}\)El número\(x-i y\) se llama el conjugado de\(z\), escrito\(\bar{z}\).
OBSERVACIÓN. Hay un punto importante a tener en cuenta sobre el argumento: sólo es único hasta la adición de múltiplos de\(2 \pi\). En otras palabras, si\(\theta_{0}\) es un argumento del número complejo\(z\), entonces también lo son todos los números\(\left\{\theta_{0}+2 k \pi: k \in \mathbb{Z}\right\}\). La adición es más fácil en coordenadas cartesianas: agregar las partes reales e imaginarias. La multiplicación es más fácil en coordenadas polares: multiplicar los módulos y sumar los argumentos.
Proposición 9.19. Dejar\(z_{1}=r_{1} \operatorname{Cis}\left(\theta_{1}\right)\) y\(z_{2}=r_{2} \operatorname{Cis}\left(\theta_{2}\right)\). Después\[z_{1} z_{2}=r_{1} r_{2} \operatorname{Cis}\left(\theta_{1}+\theta_{2}\right) .\] Prueba. Multiplicando, obtenemos\[\begin{aligned} z_{1} z_{2}=r_{1} r_{2}\left[\cos \theta_{1} \cos \theta_{2}-\sin \theta_{1} \sin \theta_{2}\right.\\ &\left.+i\left(\cos \theta_{1} \sin \theta_{2}+\cos \theta_{2} \sin \theta_{1}\right)\right] . \end{aligned}\] El resultado sigue por las identidades trigonométricas para el coseno y el seno de la suma de dos ángulos.
Una consecuencia de la Proposición\(9.19\) es la siguiente fórmula para elevar un número complejo a una potencia, llamada teorema de De Moivre.
TEOREMA 9.20. Teorema de De Moivre Let\(z=r \operatorname{Cis}(\theta)\) be a nonzero complex number, and let\(n \in \mathbb{Z}\). Después\[z^{n}=r^{n} \operatorname{Cis}(n \theta) .\] Prueba. Si\(n \geq 0\), entonces se\((9.21)\) puede probar por inducción a partir de la Proposición 9.19. Por\(n\) negativo, basta con observar que por Proposición Ahora\(9.19\)\[[r \operatorname{Cis}(\theta)]\left[r^{-1} \operatorname{Cis}(-\theta)\right]=1 \operatorname{Cis}(0)=1 .\] podemos demostrar que cada número complejo distinto de cero tiene\(n^{\text {th }}\) raíces exactamente\(n\) distintas.
TEOREMA 9.22. Dejar\(z=r \operatorname{Cis}(\theta)\) ser un número complejo distinto de cero, y dejar\(n\) ser un entero mayor que 1. Entonces hay exactamente números\(n\) complejos que\(w\) satisfacen la ecuación\(w^{n}=z\). Ellos son\[\left\{r^{1 / n} \operatorname{Cis}\left(\frac{\theta}{n}+\frac{2 k \pi}{n}\right): k=0,1, \ldots, n-1\right\} .\] Prueba. Supongamos que\(w=\rho \operatorname{Cis}(\phi)\) es una\(n^{\text {th }}\) raíz de\(z\). Entonces por el teorema de De Moivre,\(\rho^{n}=r\) y\(n \phi\) es un argumento de\(z\). Como\(\rho\) debe ser un número real positivo, es la\(n^{\text {th }}\) raíz positiva única de\(r\). El número\(n \phi\) puede ser cualquier argumento de\(z\), así que tenemos\[n \phi=\theta+2 k \pi, \quad k \in \mathbb{Z} .\] Así\(\phi\) puede tener la forma\[\frac{\theta}{n}+\frac{2 k \pi}{n}\] para cualquier entero\(k\). No obstante,\(\phi\) diferentes's darán lugar al mismo número complejo\(w\) si difieren en un múltiplo de\(2 \pi\). Entonces hay exactamente\(n\) diferentes\(w\) de las que son\(n^{\text {th }}\) raíces de\(z\).
EJEMPLO 9.24. ¿De qué nos\(9.22\) dice el Teorema son las raíces cuadradas\(-1\)? Dejamos\(r=1\) y\(\theta=\pi\), y obtenemos las raíces cuadradas son\(\operatorname{Cis}(\pi / 2)=i\) y\(\operatorname{Cis}(-\pi / 2)=-i\).
EJEMPLO 9.25. Encuentra las raíces cubicas de\(1 .\)
En la notación de Teorema\(9.22, r=1\) y\(\theta=0\). Por lo tanto las raíces cubicas son\[\begin{aligned} 1 &=\operatorname{Cis}(2 \pi / 3)=-\frac{1}{2}+i \frac{\sqrt{3}}{2} \\ \omega^{2} &=\operatorname{Cis}(4 \pi / 3)=-\frac{1}{2}-i \frac{\sqrt{3}}{2} . \end{aligned}\] El número\(\omega\) se llama una primitiva raíz cubo de la unidad, porque todas las raíces cubicas se obtienen como\(\omega, \omega^{2}, \omega^{3}\).
DEFINICIÓN. Raíz primitiva de la unidad Una\(n^{\text {th }}\) raíz primitiva de la unidad es un número\(\omega\) tal que\(\left\{1, \omega, \omega^{2}, \ldots, \omega^{n-1}\right\}\) constituye todas las\(n^{\text {th }}\) raíces de 1.
Proposición 9.26. Dejar\(z\) ser un número complejo, y\(w_{0}\) ser alguna\(n^{\text {th }}\) raíz de\(z\). \(\omega\)Sea una\(n^{\text {th }}\) raíz primitiva de unidad. Entonces todas las\(n^{\text {th }}\) raíces de\(z\) son\(\left\{w_{0}, \omega w_{0}, \omega^{2} w_{0}, \ldots, \omega^{n-1} w_{0}\right\}\).


