9.4: Teorema Fundamental del Álgebra

El álgebra sobre los números complejos es en muchos sentidos más fácil que sobre los números reales. La razón es que un polinomio de grado\(N\) en\(\mathbb{C}[z]\) tiene exactamente\(N\) ceros, contando multiplicidad. Esto se llama Teorema Fundamental del Álgebra. Para probarlo, debemos establecer algunos resultados preliminares.

Algún análisis.

DEFINICIÓN. Decimos que una secuencia\(\left\langle z_{n}=x_{n}+i y_{n}\right\rangle\) de números complejos converge al número\(z=x+i y\) iff\(\left\langle x_{n}\right\rangle\) converge a\(x\) y\(\left\langle y_{n}\right\rangle\) converge a\(y\). Decimos que la secuencia es Cauchy iff ambos\(\left\langle x_{n}\right\rangle\) y\(\left\langle y_{n}\right\rangle\) son Cauchy.

OBSERVACIÓN. Esto es lo mismo que decir que\(\left\langle z_{n}\right\rangle\) converge a\(z\) iff\(\left|z-z_{n}\right|\) tiende a cero, y eso\(\left\langle z_{n}\right\rangle\) es Cauchy iff\[(\forall \varepsilon>0)(\exists N)(\forall m, n>N)\left|z_{m}-z_{n}\right|<\varepsilon .\] DEFINICIÓN. Vamos\(G \subseteq \mathbb{C}\). Decimos que una función\(f: G \rightarrow \mathbb{C}\) es continua en\(G\) si, siempre que\(\left\langle z_{n}\right\rangle\) es una secuencia en\(G\) que converge a algún valor\(z_{\infty}\) en\(G\), entonces\(\left\langle f\left(z_{n}\right)\right\rangle\) converge a \(f\left(z_{\infty}\right)\).

PROPOSICIÓN 9.34. Los polinomios son funciones continuas en\(\mathbb{C}\).

Prueba. Repita la prueba de Proposición\(5.23\) con números complejos en lugar de números reales.

DEFINICIÓN. Un rectángulo cerrado es un conjunto de la forma\(\{z \in \mathbb{C} \mid a \leq\)\(\Re(z) \leq b, c \leq \Im(z) \leq d\}\) para algunos números reales\(a \leq b\) y\(c \leq d\). Nos gustaría una versión del Teorema del Valor Extremo, pero no está claro cómo deben definirse los valores mínimo y máximo de una función valorada compleja. Sin embargo, nuestra definición de continuidad tiene sentido incluso si el rango de\(f\) está contenido en\(\mathbb{R}\), y cada función continua de valor complejo\(g\) tiene tres funciones continuas de valor real asociadas naturalmente, a saber,\(\Re(g), \Im(g)\) y \(|g|\).

TEOREMA 9.35. Dejar\(R\) ser un rectángulo cerrado en\(\mathbb{C}\), y función\(f: R \rightarrow \mathbb{R} a\) continua. Después\(f\) alcanza su máximo y su mínimo.

Prueba. Vamos\(R=\{z \in \mathbb{C} \mid a \leq \Re(z) \leq b, c \leq \Im(z) \leq d\}\). Dejar\(\left\langle z_{n}=x_{n}+i y_{n}\right\rangle\) ser una secuencia de puntos tal que\(f\left(z_{n}\right)\) tiende o bien al límite inferior superior del rango de\(f\), si esto existe, o dejar\(f\left(z_{n}\right)>n\) para todos\(n\), si el rango no está delimitado por encima. Por el Teorema de BolzanoWeiersTrass 8.6, hay alguna subsecuencia para la cual las partes reales convergen a algún número\(x_{\infty}\) en\([a, b]\). Por Bolzano-Weierstrass nuevamente, alguna subsecuencia de esta subsecuencia tiene la propiedad de que las partes imaginarias también convergen, hasta cierto punto\(y_{\infty}\) en\([c, d]\). Entonces, reemplazando la secuencia original por esta subsecuencia de la subsecuencia, podemos suponer que\(z_{n}\) converge al punto\(z_{\infty}=x_{\infty}+i y_{\infty} \in R\). Por continuidad,\(f\left(z_{\infty}\right)=\lim _{n \rightarrow \infty} f\left(z_{n}\right)\). Si la secuencia original no estaba delimitada entonces\(f\left(z_{n}\right)>n\) en la subsecuencia. Esto es imposible ya que la secuencia\(\left\langle f\left(z_{n}\right)\right\rangle\) converge a\(f\left(z_{\infty}\right)\). Por lo tanto, la subsecuencia está limitada y\(f\left(z_{\infty}\right)\) debe ser el límite inferior superior del rango de\(f\). Por lo tanto\(f\left(z_{\infty}\right)\) es el máximo de\(f\) más\(R\).

Un argumento similar muestra que también se alcanza el mínimo.

OBSERVACIÓN. El teorema anterior se puede mejorar para mostrar que una función continua de valor real en un conjunto delimitado cerrado\(\mathbb{C}\) alcanza sus extremos. Un conjunto\(F\) se cierra si cada vez que una secuencia de puntos\(\left\langle z_{n}\right\rangle\) converge a algún número complejo\(z_{\infty}\), entonces\(z_{\infty}\) está adentro\(F\). Un conjunto está delimitado si está contenido en algún rectángulo.

Necesitamos un hecho geométrico más. LEMA 9.36. Desigualdad triangular Let\(z_{1}, z_{2}\) be complex numbers. Entonces\[\left|z_{1}+z_{2}\right| \leq\left|z_{1}\right|+\left|z_{2}\right|\]

FIGURA\(9.18\). Desigualdad triangular

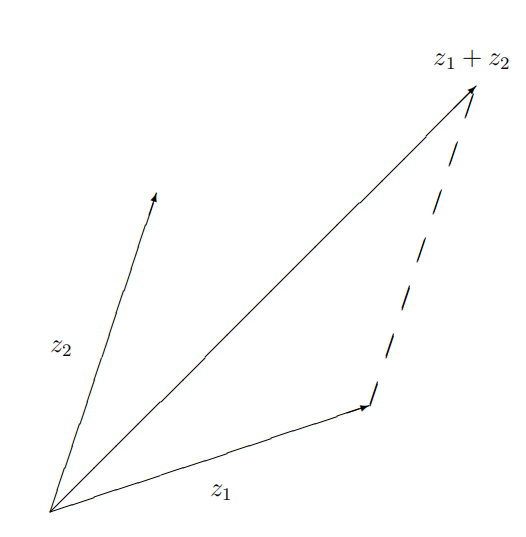
Prueba. Escribir\(z_{1}=r_{1} \operatorname{Cis}\left(\theta_{1}\right)\) y\(z_{2}=r_{2} \operatorname{Cis}\left(\theta_{2}\right)\). Después\[\begin{aligned} \left|r_{1} \operatorname{Cis}\left(\theta_{1}\right)+r_{2} \operatorname{Cis}\left(\theta_{2}\right)\right| \\ &=\left[\left(r_{1} \cos \theta_{1}+r_{2} \cos \theta_{2}\right)^{2}+\left(r_{1} \sin \theta_{1}+r_{2} \operatorname{si}\right.\right.\\ &=\left[r_{1}^{2}+r_{2}^{2}+2 r_{1} r_{2}\left(\cos \theta_{1} \cos \theta_{2}+\sin \theta_{1} \sin \theta_{2}\right)\right] \\ &=\left[r_{1}^{2}+r_{2}^{2}+2 r_{1} r_{2} \cos \left(\theta_{1}-\theta_{2}\right)\right]^{1 / 2} \\ & \leq\left[r_{1}^{2}+r_{2}^{2}+2 r_{1} r_{2}\right]^{1 / 2} \\ &=r_{1}+r_{2} . \end{aligned}\] COROLARIO 9.38. Vamos\(z_{1}, \ldots, z_{n} \in \mathbb{C}\). Entonces\[\left|z_{1}+\cdots+z_{n}\right| \leq\left|z_{1}\right|+\cdots+\left|z_{n}\right| .\]

La Prueba del Teorema Fundamental del Álgebra.

Primero observamos que encontrar raíces y factores de hallazgo están estrechamente relacionados.

LEMA 9.39. Dejar\(p\) ser un polinomio de grado\(N \geq 1\) en\(\mathbb{C}[z]\). Un número complejo,\(c\), es una raíz de\(p\) iff\[p(z)=(z-c) q(z),\] donde\(q\) es un polinomio de grado\(N-1\).

Prueba. Repita la prueba de Lema\(4.13\) con números reales reemplazados por números complejos.

Ahora probamos el lema de D'Alembert, que establece que el módulo de un polinomio no puede tener un mínimo local excepto en una raíz.

LEMA 9.40. Lema de D'Alembert Let\(p \in \mathbb{C}[z]\) y\(\alpha \in \mathbb{C}\). Si\(p(\alpha) \neq 0\), entonces\[(\forall \varepsilon>0)(\exists \zeta)[|\zeta-\alpha|<\varepsilon] \wedge[|p(\zeta)|<|p(\alpha)|]\] Prueba. Arreglar\(\alpha\), no una raíz de\(p\). Escribe\(p\) como\[p(z)=\sum_{k=0}^{N} a_{k}(z-\alpha)^{k},\] donde ni\(a_{0}\) ni\(a_{N}\) están 0. Que\[m=\min \left\{j \in \mathbb{N}^{+} \mid a_{j} \neq 0\right\} .\] Así\[p(z)=a_{0}+a_{m}(z-\alpha)^{m}+\cdots+a_{N}(z-\alpha)^{N} .\] Que Que\(a_{0}=r_{0} \operatorname{Cis}\left(\theta_{0}\right)\) Y\(a_{m}=r_{m} \operatorname{Cis}\left(\theta_{m}\right)\). Elegiremos\(\zeta\) de la forma de tal\[\zeta=\alpha+\rho \operatorname{Cis}(\phi)\] manera que obtengamos alguna cancelación en los dos primeros términos de (9.42). Entonces, vamos\[\phi=\frac{\theta_{0}+\pi-\theta_{m}}{m} .\] Entonces\[a_{0}+a_{m}(\zeta-\alpha)^{m}=r_{0} \operatorname{Cis}\left(\theta_{0}\right)-r_{m} \rho^{m} \operatorname{Cis}\left(\theta_{0}\right) .\] Queda por demostrar que, por lo suficientemente\(\rho\) pequeño, podemos ignorar todos los términos de orden superior. Tenga en cuenta que si\(\rho<1\), tenemos\[\begin{aligned} \left|a_{m+1}(\zeta-\alpha)^{m+1}+\cdots+a_{N}(\zeta-\alpha)^{N}\right| \\ & \leq\left|a_{m+1}(\zeta-\alpha)^{m+1}\right|+\cdots+\left|a_{N}(\zeta-\alpha)^{N}\right| \\ &=\left|a_{m+1}\right| \rho^{m+1}+\cdots+\left|a_{N}\right| \rho^{N} \\ & \leq \rho^{m+1}\left[\left|a_{m+1}\right|+\cdots+\left|a_{N}\right|\right] \\ &=: C \rho^{m+1} . \end{aligned}\] Elige\(\rho\) para que\(r_{m} \rho^{m}<r_{0}\). Entonces\[p(\zeta)=\left(r_{0}-r_{m} \rho^{m}\right) \operatorname{Cis}\left(\theta_{0}\right)+a_{m+1}(\zeta-\alpha)^{m+1}+\cdots+a_{N}(\zeta-\alpha)^{N},\]\(\mathrm{SO}\)\[|p(\zeta)| \leq r_{0}-r_{m} \rho^{m}+C \rho^{m+1} .\] Si\(\rho<r_{m} / C\), el lado derecho de (9.43) es menor que\(r_{0}\).

Entonces concluimos que al tomar\[\rho=\frac{1}{2} \min \left(1, \frac{r_{m}}{C},\left[\frac{r_{0}}{r_{m}}\right]^{1 / m}, \varepsilon\right)\] entonces\[\zeta=\rho \operatorname{Cis}\left(\frac{\theta_{0}+\pi-\theta_{m}}{m}\right)\] satisface la conclusión del lema.

TEOREMA 9.44. Teorema Fundamental de Álgebra Let\(p \in \mathbb{C}[z]\) Ser un polinomio de grado\(N \geq 1\). Entonces se\(p\) puede factorizar como\[p(z)=c\left(z-\alpha_{1}\right) \ldots\left(z-\alpha_{N}\right)\] para números complejos\(c, \alpha_{1}, \ldots, \alpha_{N}\). Además, el factoring es único hasta el orden. Prueba. (i) Mostrar que\(p\) tiene al menos una raíz.

Vamos\(p(z)=\sum_{k=0}^{N} a_{k} z^{k}\), con\(a_{N} \neq 0\). Dejar\(S\) ser el cuadrado cerrado\(\{z \in \mathbb{C} \mid-L \leq \Re(z) \leq L,-L \leq \Im(z) \leq L\}\), donde\(L\) hay algún número (grande) para ser elegido posteriormente.

Si\(|z|=R\) entonces\[\left|\sum_{k=0}^{N-1} a_{k} z^{k}\right| \leq \sum_{k=0}^{N-1}\left|a_{k}\right| R^{k} .\] Elige\(L_{0}\) para que si\(R \geq L_{0}\),\[\sum_{k=0}^{N-1}\left|a_{k}\right| R^{k} \leq \frac{1}{2}\left|a_{N}\right| R^{N} .\] entonces Entonces si\(L \geq L_{0}\) y\(z\) está afuera\(S\), tenemos\[\begin{aligned} \left|a_{N} z^{N}\right| &=\left|p(z)-\sum_{k=0}^{N-1} a_{k} z^{k}\right| \\ & \leq|p(z)|+\left|\sum_{k=0}^{N-1} a_{k} z^{k}\right| \\ & \leq|p(z)|+\frac{1}{2}\left|a_{N}\right| L^{N}, \end{aligned}\] donde el primero la desigualdad es el triángulo de la desigualdad, y el segundo porque\(|z|>L\). Elija\(L_{1}\) tal que\[\frac{1}{2}\left|a_{N}\right| L_{1}^{N}>\left|a_{0}\right| .\] Let\(L=\max \left(L_{0}, L_{1}\right)\), y deje\(S\) ser el cuadrado cerrado correspondiente. La función\(|p|\) es continua\(S\), por lo que alcanza su mínimo en algún momento,\(\alpha_{1}\) digamos, por el Teorema 9.35. En el límite de\(S\), sabemos\[|p(z)| \geq \frac{1}{2}\left|a_{N}\right| L^{N}>\left|a_{0}\right|=|p(0)| .\] Por lo tanto\(\alpha_{1}\) debe estar en el interior de\(S\). Por el lema de D'Alembert, debemos tener\(p\left(\alpha_{1}\right)=0\), o de lo contrario habría un punto cercano\(\zeta\), también en\(S\), donde\(|p(\zeta)|\) era más pequeño que\(\left|p\left(\alpha_{1}\right)\right|\). Entonces\(\alpha_{1}\) es una raíz de\(p\).

(ii) Ahora aplicamos Lema\(9.39\) para concluir que podemos factorial\(p\) como\[p(z)=\left(z-\alpha_{1}\right) q(z)\] dónde\(q\) está un polinomio de grado\(N-1\). Por un argumento directo de inducción, podemos factorial\(p\) en factores\(N\) lineales.

(iii) La singularidad es obvia. El número\(c\) es el coeficiente\(a_{N}\). Los números\(a_{k}\) son precisamente los puntos en los que la función\(p\) desaparece, ya que de Proposición se deduce\(9.19\) que el producto de finitamente muchos números complejos puede ser 0 si y solo si uno de los números es en sí mismo 0.