5.1: Axiomas de los números reales

En este capítulo profundizaremos en la estructura de los números reales construyendo la multitud de propiedades con las que está familiarizado comenzando con una colección de axiomas fundamentales. Recordemos que un axioma es una afirmación que se supone que es verdadera sin pruebas. Estos son los bloques básicos a partir de los cuales se prueban todos los teoremas. Cabe señalar que uno puede construir cuidadosamente los números reales a partir de los números naturales. No obstante, ese no será el enfoque que adoptemos. En cambio, simplemente enumeraremos los axiomas que satisfacen los números reales

Nuestros axiomas para los números reales se agrupan en tres categorías:

1. Axiomas de campo: Estos axiomas proporcionan las propiedades esenciales de la aritmética que implica suma y resta.
2. Orden Axiomas: Estos axiomas proporcionan las propiedades necesarias de las desigualdades.
3. Axioma de integridad: Este axioma asegura que la línea numérica familiar que usamos para modelar los números reales no tenga ningún agujero en ella.

Comenzamos con los Axiomas de Campo.

Axiomas 5.1. Existen operaciones\(+\) (suma) y\(\cdot\) (multiplicación) sobre\(\mathbb{R}\) satisfacer:

1. (Asociatividad para la Adición) Por todo\(a, b, c\in \mathbb{R}\) lo que tenemos\((a+b)+c = a+(b+c)\);
2. (Conmutatividad para la Adición) Para todos\(a,b\in \mathbb{R}\), tenemos\(a+b=b+a\);
3. (Identidad Aditiva) Existe\(0\in\mathbb{R}\) tal que para todos\(a\in\mathbb{R}\),\(0+a=a\);
4. (Inversos Aditivos) Para todos\(a\in\mathbb{R}\) existe\(-a\in\mathbb{R}\) tal que\(a+(-a)=0\);
5. (Asociatividad para la Multiplicación) Por todo\(a, b, c\in \mathbb{R}\) lo que tenemos\((ab)c = a(bc)\);
6. (Conmutatividad para la Multiplicación) Para todos\(a,b\in \mathbb{R}\), tenemos\(ab=ba\);
7. (Identidad Multiplicativa) Existe\(1\in\mathbb{R}\) tal que\(1\neq 0\) y para todos\(a\in\mathbb{R}\),\(1a=a\);
8. (Inversiones multiplicativas) Por todos\(a\in\mathbb{R}\setminus\{0\}\) existe\(a^{-1}\in\mathbb{R}\) tal que\(aa^{-1}=1\).
9. (Propiedad distributiva) Para todos\(a,b,c\in \mathbb{R}\),\(a(b+c)=ab+ac\);

En el lenguaje del álgebra abstracta, los Axiomas F1—F4 y F5—F8 hacen cada uno de\(\mathbb{R}\) y\(\mathbb{R}\setminus\{0\}\) un grupo abeliano bajo suma y multiplicación, respectivamente. Axioma F9 proporciona una forma para que las operaciones de adición y multiplicación interactúen. Colectivamente, los Axiomas F1—F9 hacen de los números reales un campo. De los axiomas se deduce que los elementos\(0\) y\(1\) de\(\mathbb{R}\) son las identidades aditivas y multiplicativas únicas en\(\mathbb{R}\). Para probar el siguiente teorema, supongamos\(0\) y\(0'\) son ambas identidades aditivas en\(\mathbb{R}\) y luego mostrar eso\(0=0'\). Esto demuestra que sólo puede haber una identidad aditiva.

Teorema 5.2. La identidad aditiva de\(\mathbb{R}\) es única.

Para probar el siguiente teorema, imita el enfoque que utilizó para probar el Teorema 5.2.

Teorema 5.3. La identidad multiplicativa de\(\mathbb{R}\) es única.

Para cada uno\(a\in\mathbb{R}\), los elementos\(-a\) y\(a^{-1}\) (siempre y cuando\(a\neq 0\)) son también los inversos aditivos y multiplicativos únicos, respectivamente.

Teorema 5.4. Cada número real tiene una inversa aditiva única.

Teorema 5.5. Cada número real distinto de cero tiene una inversa multiplicativa única.

Dado que estamos tomando un enfoque axiomático formal de los números reales, debemos dejar claro cómo están incrustados los números naturales\(\mathbb{R}\).

Definición 5.6. Definimos los números naturales, denotados por\(\mathbb{N}\), como el subconjunto más pequeño de\(\mathbb{R}\) satisfacción:

1. \(1\in\mathbb{N}\), y
2. para todos\(n\in\mathbb{N}\), tenemos\(n+1\in\mathbb{N}\).

Observe la similitud entre la definición de los números naturales presentados anteriormente y el Axioma de Inducción dado en la Sección 4.1. Por supuesto, utilizamos el sistema numérico estándar para representar los números naturales, así que eso\(\mathbb{N}= \{1,2,3,4,5,6,7,8,9,10\ldots\}\).

Dados los números naturales, Axioma F3/Teorema 5.2 y Axioma F4/Teorema 5.4 junto con la operación de adición nos permiten definir los enteros, denotados por\(\mathbb{Z}\), de la manera obvia. Es decir, los enteros consisten en los números naturales junto con la identidad aditiva y todas las inversas aditivas de los números naturales.

Ahora introducimos alguna notación común con la que probablemente esté familiarizado. Tómese un momento para pensar por qué lo siguiente es una definición a diferencia de un axioma o teorema.

Definición 5.7. Para cada\(a,b\in\mathbb{R}\) y\(n\in\mathbb{Z}\), definimos lo siguiente:

1. \(a-b:= a+(-b)\)
2. \(\displaystyle\frac{a}{b}:= ab^{-1}\)(para\(b\neq 0\))
3. \(\displaystyle a^n:= \begin{cases} \overbrace{aa\cdots a}^n, &\text{if }n\in \mathbb{N}\\ 1, & \text{if }n=0\text{ and }a\neq 0\\ \displaystyle\frac{1}{a^{-n}}, & \text{if }-n\in \mathbb{N}\text{ and }a\neq 0 \end{cases}\)

El conjunto de números racionales, denotado por\(\mathbb{Q}\), se define como el conjunto de todos los números reales que tienen la forma dada en la Parte (b) de la Definición 5.7 Los números irracionales se definen para ser\(\mathbb{R}\setminus\mathbb{Q}\).

Utilizando los Axiomas de Campo, podemos probar cada una de las afirmaciones en el siguiente teorema.

Teorema 5.8. Para todos\(a,b,c\in\mathbb{R}\), tenemos lo siguiente:

1. \(a=b\)si y sólo si\(a+c=b+c\);
2. \(0a=0\);
3. \(-a=(-1)a\);
4. \((-1)^2 = 1\);
5. \(-(-a)=a\);
6. Si\(a\neq 0\), entonces\((a^{-1})^{-1}=a\);
7. Si\(a\neq 0\) y\(ab = ac\), entonces\(b = c\).
8. Si\(ab=0\), entonces cualquiera\(a=0\) o\(b=0\).

Prueba cuidadosamente el siguiente teorema citando explícitamente dónde estás utilizando los Axiomas de Campo y Teorema 5.8.

Teorema 5.9. Para todos\(a,b\in\mathbb{R}\), tenemos\((a+b)(a-b)=a^2-b^2\).

Presentamos ahora los Axiomas de Orden de los números reales.

Axiomas 5.10. Porque\(a,b,c\in \mathbb{R}\), hay una relación\(<\) en\(\mathbb{R}\) satisfacer:

1. (Ley de Tricotomía) Si\(a\neq b\), entonces cualquiera\(a<b\) o\(b<a\) pero no ambos;
2. (Transitividad) Si\(a<b\) y\(b<c\), entonces\(a<c\);
3. Si\(a<b\), entonces\(a+c<b+c\);
4. Si\(a<b\) y\(0<c\), entonces\(ac<bc\);

Dados los Axiomas 1—4, decimos que los números reales son un campo linealmente ordenado. Llamamos a números mayores que cero positivos y a los mayores o iguales a cero no negativos. Existen definiciones similares para negativo y no positivo.

Observe que los Axiomas de la Orden están formulados en términos de “\(<\)”. También nos gustaría poder utilizar ““,\(>\)\(\leq\) “, y “\(\geq\)”.

Definición 5.11. Para\(a,b\in\mathbb{R}\), definimos:

1. \(a>b\)si\(b<a\);
2. \(a\leq b\)si\(a<b\) o\(a=b\);
3. \(a\geq b\)si\(b\leq a\).

Observe que tomamos por sentada la existencia de las desigualdades\(<\) “\(>\)“, “\(\leq\)“, “y “\(\geq\)" sobre los números reales cuando definimos intervalos de números reales en la Definición 3.4.

Usando los Axiomas de la Orden, podemos probar muchos hechos familiares.

Teorema 5.12. Para todos\(a,b\in\mathbb{R}\), si\(a,b>0\), entonces\(a+b>0\); y si\(a,b<0\), entonces\(a+b<0\).

El siguiente resultado se extiende Axioma 3.

Teorema 5.13. Para todos\(a,b,c,d\in\mathbb{R}\), si\(a<b\) y\(c<d\), entonces\(a+c<b+d\).

Teorema 5.14. Para todos\(a\in\mathbb{R}\),\(a>0\) si y solo si\(-a<0\).

Teorema 5.15. Si\(a\),\(b\),\(c\), y\(d\) son números reales positivos tales que\(a<b\) y\(c<d\), entonces\(ac<bd\).

Teorema 5.16. Para todos\(a,b\in\mathbb{R}\), tenemos lo siguiente:

1. \(ab>0\)si y sólo si\(a,b>0\) o\(a,b<0\);
2. \(ab<0\)si y sólo si\(a<0<b\) o\(b<0<a\).

Teorema 5.17. Para todos los números reales positivos\(a\) y\(b\),\(a< b\) si y sólo si\(a^2< b^2\).

Considere utilizar tres casos al acercarse a la prueba del siguiente teorema.

Teorema 5.18. Para todos\(a\in\mathbb{R}\), tenemos\(a^2\geq 0\).

Podría ser una sorpresa que el siguiente resultado requiera pruebas.

Teorema 5.19. Tenemos\(0<1\).

El teorema anterior junto con el Teorema 5.14 implica que\(-1<0\) como se espera. También se desprende del Axioma O3 que para todos\(n\in\mathbb{Z}\), tenemos\(n<n+1\). Suponemos que no hay números enteros entre\(n\) y\(n+1\).

Teorema 5.20. Para todos\(a\in\mathbb{R}\), si\(a>0\), entonces\(a^{-1}>0\), y si\(a<0\), entonces\(a^{-1}<0\).

Teorema 5.21. Para todos\(a,b\in \mathbb{R}\), si\(a<b\), entonces\(-b<-a\).

Los últimos resultados nos permiten dar por sentado nuestra comprensión habitual de qué números reales son positivos y cuáles negativos. El siguiente teorema arroja un resultado que extiende el Teorema 5.21.

Teorema 5.22. Para todos\(a,b,c\in \mathbb{R}\), si\(a<b\) y\(c<0\), entonces\(bc<ac\).

Hay una función especial que ahora podemos introducir.

Definición 5.23. Dado\(a\in\mathbb{R}\), definimos el valor absoluto de\(a\), denotado\(|a|\), vía\[|a|:= \begin{cases} a, & \text{if }a\geq 0\\ -a, & \text{if }a<0. \end{cases}\]

Teorema 5.24. Para todos\(a\in\mathbb{R}\),\(|a|\geq 0\) con igualdad sólo si\(a=0\).

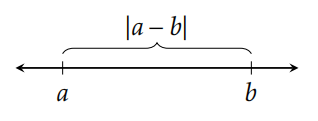
Podemos interpretar\(|a|\) como la distancia entre\(a\) y 0 como se representa en la Figura 5.1.

Figura 5.1: Representación visual de |a|.

Teorema 5.25. Para todos\(a,b\in\mathbb{R}\), tenemos\(|a-b|=|b-a|\).

Dados dos puntos\(a\) y\(b\),\(|a-b|\), y\(|b-a|\) por lo tanto por el teorema anterior, se encuentra la distancia entre\(a\) y\(b\) como se muestra en la Figura 5.2.

Figura 5.2: Representación visual de |a − b|.

Teorema 5.26. Para todos\(a,b\in\mathbb{R}\),\(|ab|=|a||b|\).

En el siguiente teorema, la escritura\(\pm a\leq b\) es una abreviatura de\(a\leq b\) y\(-a\leq b\).

Teorema 5.27. Para todos\(a,b\in\mathbb{R}\), si\(\pm a\leq b\), entonces\(|a|\leq b\).

Teorema 5.28. Para todos\(a\in\mathbb{R}\),\(|a|^2=a^2\).

Teorema 5.29. Para todos\(a\in\mathbb{R}\),\(\pm a\leq |a|\).

Figura 5.3: Representación visual de |a| ≤ r.

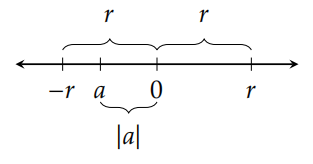
Teorema 5.30. Para todos\(a,r\in\mathbb{R}\) con\(r\) no negativo,\(|a|\leq r\) si y solo si\(-r\leq a\leq r\).

La letra\(r\) se utilizó en el teorema anterior porque es la primera letra de la palabra “radio”. Si\(r\) es positivo, podemos pensar en el intervalo\((-r,r)\) como el interior de un círculo unidimensional con radio\(r\) centrado en 0. La Figura 5.3 proporciona una interpretación visual del Teorema 5.30.

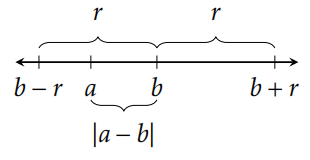
Corolario 5.31. Para todos\(a,b,r\in\mathbb{R}\) con\(r\) no negativo,\(|a-b|\leq r\) si y solo si\(b-r\leq a\leq b+r\).

Ya que\(|a-b|\) representa la distancia entre\(a\) y\(b\), podemos interpretar\(|a-b|\leq r\) como diciendo que la distancia entre\(a\) y\(b\) es menor o igual a\(r\). En otras palabras,\(a\) está dentro de\(r\) unidades de\(b\). Ver Figura 5.4.

Figura 5.4: Representación visual de |a − b| ≤ r.

Considera usar los Teoremas 5.29 y 5.30 al atacar el siguiente resultado, que se conoce como la Desigualdad del Triángulo. Este resultado puede ser extremadamente útil en algunos contextos.

Teorema 5.32. Para todos\(a,b\in\mathbb{R}\),\(|a+b|\leq |a|+|b|\).

La Figura 5.5 representa dos de los casos para la Desigualdad del Triángulo.

Figura 5.5: Representación visual de dos de los casos para la Desigualdad del Triángulo

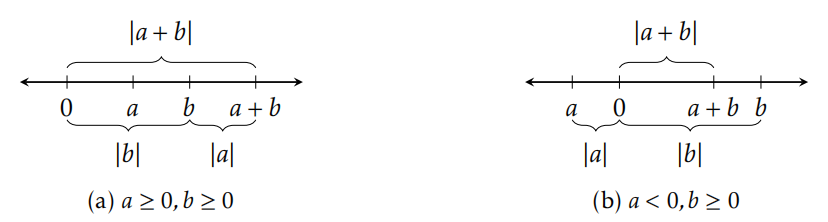
Problema 5.33. ¿Bajo qué condiciones tenemos igualdad para el Triángulo Desigualdad?

¿De dónde obtuvo su nombre el Triángulo Desigualdad? ¿Por qué “Triángulo”? Para cualquier triángulo (incluidos los triángulos degenerados), la suma de las longitudes de cualquiera de los dos lados debe ser mayor o igual que la longitud del lado restante. Es decir, si\(x\)\(y\),, y\(z\) son las longitudes de los lados del triángulo, entonces\(z\leq x+y\), donde tenemos igualdad sólo en el caso degenerado de un triángulo sin área. En álgebra lineal, la Desigualdad del Triángulo es un teorema sobre longitudes de vectores. Si\(\mathbf{a}\) y\(\mathbf{b}\) son vectores en\(\mathbb{R}^n\), entonces el Triángulo Desigualdad lo afirma\(\lVert \mathbf{a}+\mathbf{b}\rVert \leq \lVert\mathbf{a}\rVert +\lVert\mathbf{b}\rVert\). Tenga en cuenta que\(\lVert \mathbf{a}\rVert\) denota la longitud del vector\(\mathbf{a}\). Ver Figura 5.6. La versión del Triángulo Desigualdad que presentamos en el Teorema 5.32 es precisamente la versión unidimensional del Triángulo Desigualdad en términos de vectores.

Figura 5.6: Desigualdad triangular en términos de vectores.

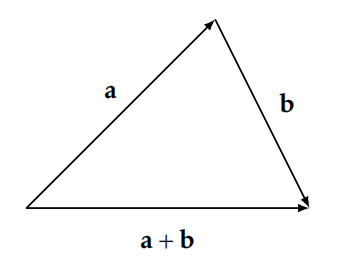
El siguiente teorema se llama a veces la Desigualdad del Triángulo Inverso.

Theroem 5.34. Para todos\(a,b\in\mathbb{R}\),\(|a-b|\geq \left||a|-|b| \right|\).

Antes de introducir el Axioma de la Integtud, necesitamos algo de terminología adicional.

Definición 5.35. Vamos\(A\subseteq \mathbb{R}\). Un punto\(b\) se llama límite superior de\(A\) si para todos\(a\in A\),\(a\leq b\). \(A\)Se dice que el conjunto está delimitado arriba si tiene un límite superior.

Problema 5.36. La noción de un límite inferior y la propiedad de un conjunto que se limita a continuación se definen de manera similar. Intenta definirlos.

Problema 5.37. Encuentra todos los límites superiores y todos los límites inferiores para cada uno de los siguientes conjuntos cuando existan.

1. \(\{5,11,17,42,103\}\)
2. \(\mathbb{N}\)
3. \(\mathbb{Z}\)
4. \((0,1]\)
5. \((0,1]\cap \mathbb{Q}\)
6. \((0,\infty)\)
7. \(\{42\}\)
8. \(\{\frac{1}{n}\mid n\in\mathbb{N}\}\)
9. \(\{\frac{1}{n}\mid n\in\mathbb{N}\}\cup\{0\}\)
10. \(\emptyset\)

Definición 5.38. Un conjunto\(A\subseteq \mathbb{R}\) está delimitado si\(A\) está delimitado por encima y por debajo.

Observe que un conjunto\(A\subseteq\mathbb{R}\) está delimitado si y solo si es un subconjunto de algún intervalo cerrado delimitado.

Definición 5.39. Vamos\(A\subseteq \mathbb{R}\). Un punto\(p\) es un límite supremo (o menos superior) de\(A\) si\(p\) es un límite superior de\(A\) y\(p\leq b\) para cada límite superior\(b\) de\(A\). Análogamente, un punto\(p\) es un infimum (o mayor límite inferior) de\(A\) si\(p\) es un límite inferior de\(A\) y\(p\geq b\) para cada límite inferior\(b\) de \(A\).

Nuestro siguiente resultado nos dice que un supremo de un conjunto y un infimum de un conjunto son únicos cuando existen.

Teorema 5.40. Si\(A\subseteq \mathbb{R}\) tal que\(A\) existe un supremum (respectivamente, infimum), entonces el supremum (respectivamente, infimum) de\(A\) es único.

A la luz del teorema anterior, si el supremo de\(A\) existe, se denota por\(\sup(A)\). De igual manera, si el infimum de\(A\) existe, se denota por\(\inf(A)\).

Problema 5.41. Encuentra lo supremo y el infimum de cada uno de los conjuntos en Problema 5.37 cuando existan.

Es importante reconocer que el supremo o infimum de un conjunto puede o no estar contenido en el conjunto. En particular, tenemos el siguiente teorema referente a suprema y máximos. El resultado análogo se mantiene para infima y mínimos.

Teorema 5.42. Vamos\(A\subseteq \mathbb{R}\). Entonces\(A\) tiene un máximo si y sólo si\(A\) tiene un supremo y\(\sup(A)\in A\), en cuyo caso el\(\max(A)=\sup(A)\).

Intuitivamente, un punto es el supremo de un conjunto\(A\) si y solo si ningún punto menor que el supremo puede ser un límite superior de\(A\). El siguiente resultado lo hace más preciso.

Teorema 5.43. Que\(A\subseteq \mathbb{R}\) tal que\(A\) quede delimitado arriba y deje\(b\) ser un límite superior de\(A\). Entonces\(b\) es lo supremo de\(A\) si y solo si por cada\(\varepsilon >0\), existe\(a\in A\) tal que\(b-\varepsilon <a\).

Problema 5.44. Estado y probar el resultado análogo al Teorema 5.43 involucrando infimum.

El siguiente axioma establece que cada subconjunto no vacío de los números reales que tiene un límite superior tiene un límite superior mínimo.

Axiomas 5.45. Si\(A\) es un subconjunto no vacío de\(\mathbb{R}\) eso está delimitado arriba, entonces\(\sup(A)\) existe.

Dado el Axioma de la Integtud, decimos que los números reales satisfacen la menor propiedad de límite superior. Cabe mencionar que no necesitamos el Axioma de la Integtud para concluir que cada subconjunto no vacío de los enteros que está delimitado arriba tiene un supremo, como esto se desprende del Teorema 4.40 (una versión generalizada del Principio de Ordenación del Bien).

Ciertamente, los números reales también satisfacen el resultado análogo que involucra infimum.

Teorema 5.46. Si\(A\) es un subconjunto no vacío de\(\mathbb{R}\) eso está delimitado por debajo, entonces\(\inf(A)\) existe.

Nuestro siguiente resultado, llamado la Propiedad de Arquímedes, nos dice que por cada número real, siempre podemos encontrar un número natural que sea mayor. Para probar este teorema, considere una prueba por contradicción y luego utilice el Axioma y Teorema de la Integtud 5.43.

Teorema 5.47. Por cada\(x\in\mathbb{R}\), existe\(n\in\mathbb{N}\) tal que\(x<n\).

De manera más general, podemos “exprimir” cada número real entre un par de enteros. El siguiente resultado se refiere a veces en la Propiedad Arquímedes Generalizada.

Teorema 5.48. Por cada\(x\in\mathbb{R}\), existe\(k,n\in\mathbb{Z}\) tal que\(k<x<n\).

Teorema 5.49. Para cualquier número real positivo\(x\), existe\(N\in \mathbb{N}\) tal que\(0<\frac{1}{N}<x\).

El siguiente teorema fortalece la Propiedad de Arquímedes Generalizada y dice que cada número real es o bien un entero o se encuentra entre un par de enteros consecutivos. Para probar este teorema, dejar\(x\in\mathbb{R}\) y definir\(L=\{k\in\mathbb{Z}\mid k\leq x\}\). Utilice la Propiedad de Arquímedes Generalizada para concluir que no\(L\) está vacía y luego utilizar el Teorema 4.40.

Teorema 5.50. Por cada\(x\in\mathbb{R}\), existe\(n\in \mathbb{Z}\) tal que\(n\leq x<n+1\).

Para probar el siguiente teorema, vamos\(a<b\), utilizar el Teorema 5.49\(b-a\) para obtener\(N\in\mathbb{N}\) tal que\(\frac{1}{N}<b-a\), y luego aplicar Teorema 5.50\(Na\) para concluir que existe\(n\in\mathbb{N}\) tal que \(n\leq Na<n+1\). Por último, argumenta que\(\frac{n+1}{N}\) es el número racional que buscas.

Teorema 5.51. Si\((a,b)\) es un intervalo abierto, entonces existe un número racional\(p\) tal que\(p\in(a,b)\).

Recordemos que los números reales consisten en números racionales e irracionales. Dos ejemplos de un número irracional con el que probablemente estés familiarizado son\(\pi\) y\(\sqrt{2}\). En la Sección 6.2, vamos a demostrar que\(\sqrt{2}\) es irracional, pero por ahora vamos a dar por sentado este hecho. Resulta que\(\sqrt{2}\approx 1.41421356237\in (1,2)\). Esto proporciona un ejemplo de un número irracional que ocurre entre un par de números racionales distintos. El siguiente teorema es un buen reto para generalizar esto.

Teorema 5.52. Si\((a,b)\) es un intervalo abierto, entonces existe un número irracional\(p\) tal que\(p\in(a,b)\).

Aplicaciones repetidas de los dos teoremas anteriores implica que cada intervalo abierto contiene infinitamente muchos números racionales e infinitamente muchos números irracionales. A la luz de estos dos teoremas, decimos que tanto los racionales como los irracionales son densos en los números reales.