8.3: Composiciones y funciones inversas

Comenzamos esta sección con un método para combinar dos funciones juntas que tienen dominios y codominios compatibles.

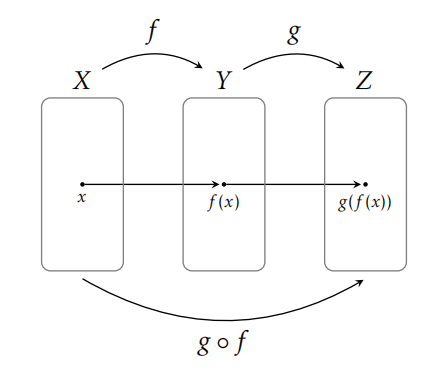
Definición 8.51. Si\(f:X\to Y\) y\(g:Y\to Z\) son funciones, definimos\(g\circ f:X\to Z\) vía\((g\circ f)(x)=g(f(x))\). La función\(g\circ f\) se llama la composición de\(f\) y\(g\).

Es importante notar que la función de la derecha es la que “va primero”. Además, no podemos componer dos funciones aleatorias ya que el codominio de la primera función debe estar de acuerdo con el dominio de la segunda función. En particular,\(f\circ g\) puede no ser una función sensata aunque\(g\circ f\) exista. La Figura 8.4 proporciona una representación visual de la composición de funciones en términos de diagramas de funciones.

Figura 8.4: Representación visual de la composición de la función.

Problema 8.52. Dejar\(X=\{1,2,3,4\}\) y definir\(f:X\to X\) y\(g:X\to X\) vía\[f=\{(1,1),(2,3),(3,3),(4,4)\}\] y\[g=\{(1,1),(2,2),(3,1),(4,1)\}.\] Para cada una de las siguientes funciones, dibuje el diagrama de funciones correspondiente en el espíritu de la Figura 8.4 e identifique el rango.

1. \(g\circ f\)
2. \(f\circ g\)

El problema anterior lo ilustra\(f\circ g\) y no\(g\circ f\) necesita ser igual incluso cuando existen ambas funciones compuestas.

Ejemplo 8.53. Considere el mapa de inclusión\(\iota:X\to Y\) tal que\(X\) sea un subconjunto apropiado de\(Y\) y supongamos que\(f:Y\to Z\) es una función. Entonces la función compuesta\(f\circ \iota:X\to Z\) es dada por\[f\circ \iota(x)=f(\iota(x))=f(x)\] para todos\(x\in X\). Observe que\(f\circ \iota\) es simplemente la función\(f\) pero con un dominio más pequeño. En este caso, decimos que\(f\circ \iota\) es la restricción de\(f\) a\(X\), que muchas veces se denota por\(f|_X\).

Problema 8.54. Definir\(f:\mathbb{R}\to \mathbb{R}\) y\(g:\mathbb{R}\to \mathbb{R}\) vía\(f(x)=x^2\) y\(g(x)=3x-5\), respectivamente. Determinar fórmulas para las funciones compuestas\(f\circ g\) y\(g\circ f\).

Problema 8.55. Definir\(f:\mathbb{R}\to \mathbb{R}\) y\(g:\mathbb{R}\to \mathbb{R}\) vía\[f(x)=\begin{cases} 5x+7, & \text{if }x< 0\\ 2x+1, & \text{if }x\geq 0 \end{cases}\] y\(g(x)=7x-11\), respectivamente. Encuentra una fórmula para la función compuesta\(g\circ f\).

Problema 8.56. Definir\(f:\mathbb{Z}/15\mathbb{Z}\to \mathbb{Z}/23\mathbb{Z}\) y\(g:\mathbb{Z}/23\mathbb{Z}\to \mathbb{Z}/32\mathbb{Z}\) vía\(f([x]_{15})=[3x+5]_{23}\) y\(g([x]_{23})=[2x+1]_{32}\), respectivamente. Encuentra una fórmula para la función compuesta\(g\circ f\).

El siguiente resultado proporciona una idea de dónde obtuvo su nombre el mapa de identidad.

Teorema 8.57. Si\(f:X\to Y\) es una función, entonces\(f\circ i_X = f = i_Y\circ f\), dónde\(i_X\) y\(i_Y\) son los mapas de identidad en\(X\) y\(Y\), respectivamente.

El siguiente teorema nos dice que la composición de funciones es asociativa.

Teorema 8.58. Si\(f:X\to Y\),\(g:Y\to Z\), y\(h:Z\to W\) son funciones, entonces\((h\circ g)\circ f = h\circ (g\circ f)\).

Problema 8.59. En cada caso, dé ejemplos de conjuntos finitos\(X\)\(Y\), y\(Z\), y funciones\(f:X\to Y\) y\(g:Y\to Z\) que satisfagan las condiciones dadas. Dibujar un diagrama de funciones es suficiente.

1. \(f\)es suryectiva, pero no\(g\circ f\) es suryectiva.
2. \(g\)es suryectiva, pero no\(g\circ f\) es suryectiva.
3. \(f\)es inyectivo, pero no\(g\circ f\) es inyectivo.
4. \(g\)es inyectivo, pero no\(g\circ f\) es inyectivo.

Problema 8.60. Si\(f:X\to Y\) y\(g:Y\to Z\) son ambas funciones suryectivas, entonces también\(g\circ f\) es suryectiva.

Teorema 8.61. Si\(f:X\to Y\) y\(g:Y\to Z\) son ambas funciones inyectoras, entonces también\(g\circ f\) es inyectivo.

Corolario 8.62. Si\(f:X\to Y\) y\(g:Y\to Z\) son ambas bijecciones, entonces también\(g\circ f\) es una bijección.

Problema 8.63. Supongamos que\(f:X\to Y\) y\(g:Y\to Z\) son ambas funciones. Determinar si cada una de las siguientes afirmaciones es verdadera o falsa. Si una afirmación es cierta, demuéstrala. De lo contrario, proporcione un contraejemplo.

1. Si\(g\circ f\) es inyectivo, entonces\(f\) es inyectivo.
2. Si\(g\circ f\) es inyectivo, entonces\(g\) es inyectivo.
3. Si\(g\circ f\) es suryectiva, entonces\(f\) es suryectiva.
4. Si\(g\circ f\) es suryectiva, entonces\(g\) es suryectiva.

Teorema 8.64. Dejar\(f:X\to Y\) ser una función. Entonces\(f\) es inyectivo si y sólo si existe una función\(g:Y\to X\) tal que\(g\circ f=i_X\), donde\(i_X\) esta el mapa de identidad encendido\(X\).

La función\(g\) en el teorema anterior a menudo se llama inversa izquierda de\(f\).

Teorema 8.65. Dejar\(f:X\to Y\) ser una función. Entonces\(f\) es suryectiva si y sólo si existe una función\(g:Y\to X\) tal que\(f\circ g=i_Y\), donde\(i_Y\) está encendido el mapa de identidad\(Y\).

La función\(g\) en el teorema anterior a menudo se llama inversa derecha de\(f\).

Problema 8.66. Dejar\(X=\{a,b\}\) y\(Y=\{1,2\}\).

1. Proporcionar un ejemplo de una función que tiene un inverso izquierdo pero no tiene un inverso derecho. Encuentra el inverso izquierdo de tu función propuesta.
2. Proporcionar un ejemplo de una función que tiene un inverso derecho pero no tiene un inverso izquierdo. Encuentra el inverso correcto de tu función propuesta.

Problema 8.67. Definir\(f:\mathbb{R}\to\mathbb{R}\) vía\(f(x)=x^2\). \(f\)Explique por qué no tiene un inverso izquierdo ni un inverso derecho.

Problema 8.68. Definir\(f:\mathbb{R}\to[0,\infty)\) vía\(f(x)=x^2\) y\(g:[0,\infty)\to \mathbb{R}\) vía\(g(x)=\sqrt{x}\).

1. \(f\)Explique por qué no tiene un inverso izquierdo.
2. Verificar que\(g\) sea la inversa correcta de\(f\) por computación\(f\circ g(x)\).

Corolario 8.69. Si\(f:X\to Y\) y\(g:Y\to X\) son funciones satisfactorias\(g\circ f=i_X\) y\(f\circ g=i_Y\), entonces\(f\) es una biyección.

En el resultado anterior, las funciones\(f\) y\(g\) “se cancelan” entre sí. En este caso, decimos que\(g\) es un inverso de dos lados de\(f\).

Definición 8.70. Dejar\(f:X\to Y\) ser una función. La relación\(f^{-1}\) de\(Y\) a\(X\), llamada\(f\) inversa, se define vía\[f^{-1}=\{(f(x),x)\in Y\times X\mid x\in X\}.\]

Observe que llamamos\(f^{-1}\) una relación y no una función. En algunas circunstancias\(f^{-1}\) será una función y a veces no lo será. Dada una función\(f\), la relación inversa es simplemente el conjunto de pares ordenados que resulta de revertir los pares ordenados en\(f\). Cabe señalar que sólo hemos definido relaciones inversas para funciones. Sin embargo, uno puede adaptar fácilmente nuestra definición para manejar relaciones arbitrarias.

Problema 8.71. Considere la función\(f\) dada en el Ejemplo 8.2 (ver Figura 8.1). Enumere los pares ordenados en la relación\(f^{-1}\) y dibuje el dígrafo correspondiente. ¿Es\(f^{-1}\) una función?

Problema 8.72. Proporcionar un ejemplo de una función\(f:X\to Y\) tal que\(f^{-1}\) es una función. Dibujar un diagrama de funciones es suficiente.

Problema 8.73. Supongamos\(X\subseteq \mathbb{R}\) y\(f:X\to \mathbb{R}\) es una función. ¿Cuál es la relación entre la gráfica de la función\(f\) y la gráfica de la relación inversa\(f^{-1}\)?

Teorema 8.74. Dejar\(f:X\to Y\) ser una función. Entonces\(f^{-1}:Y\to X\) es una función si y sólo si\(f\) es una biyección.

Problema 8.75. Supongamos que\(f:\mathbb{R}\to \mathbb{R}\) es una función. Rellena el espacio en blanco con la frase correspondiente.

La relación\(f^{-1}\) es una función si y sólo si cada línea horizontal golpea la gráfica de\(f\).

Explique por qué esta afirmación es cierta.

Teorema 8.76. Si\(f:X\to Y\) es una biyección, entonces

1. \(f^{-1}\circ f=i_X\), y
2. \(f\circ f^{-1}=i_Y\).

Teorema 8.77. Si\(f:X\to Y\) es una biyección, entonces también\(f^{-1}:Y\to X\) es una biyección.

Teorema 8.78. Si\(f:X\to Y\) y\(g:Y\to X\) son funciones tales que\(g\circ f=i_X\) y\(f\circ g=i_Y\), entonces\(f^{-1}\) es una función y\(g=f^{-1}\).

El resultado de los Teoremas 8.76 y 8.78 es que si\(f^{-1}\) es una función, entonces es el único que satisface la propiedad inversa bilateral exhibida en Corolario 8.69 y Teorema 8.76. Es decir, las funciones inversas son únicas cuando existen. Cuando la relación\(f^{-1}\) es una función, la llamamos la función inversa de\(f\).

Problema 8.79. Dejar\(X\subseteq\mathbb{R}\) y suponer\(f:X\to\mathbb{R}\) es una función. Explicar la diferencia entre\(f^{-1}(x)\) y\([f(x)]^{-1}\). ¿Cuándo existe cada uno?

Problema 8.80. Dejar\(X,Y\subseteq\mathbb{R}\) y definir\(f:X\to Y\) vía\(f(x)=e^x\) y\(g:Y\to X\) vía\(g(x)=\ln(x)\). Identificar las mayores opciones posibles para\(X\) y para\(Y\) que\(f\) y\(g\) sean inversas entre sí.

Teorema 8.81. Si\(f:X\to Y\) es una biyección, entonces\((f^{-1})^{-1}=f\).

En el teorema anterior, restringimos nuestra atención a las bijecciones por lo que\(f^{-1}\) sería una función, haciendo así\((f^{-1})^{-1}\) una relación inversa sensata a la luz de la Definición 8.70. Si hubiéramos definido inversos para relaciones arbitrarias, entonces no habríamos necesitado exigir que la función en el Teorema 8.81 fuera una biyección. De hecho, ni siquiera necesitamos exigir que la relación sea una función. Es decir, si\(R\) es una relación de\(X\) a\(Y\), entonces\((R^{-1})^{-1}=R\), como se esperaba. De igual manera, el siguiente resultado generaliza a relaciones arbitrarias.

Teorema 8.82. Si\(f:X\to Y\) y\(g:Y\to Z\) son ambas bijecciones, entonces\((g\circ f)^{-1}=f^{-1}\circ g^{-1}\).

El teorema anterior es a veces referido como el “teorema de calcetines y zapatos”. ¿Ves como obtuvo este nombre?