1.4: El modelo de depredador-presa de Lotka-Volterra
- Page ID
- 117618
\(1.4\)El modelo de depredador-presa de Lotka-Volterra
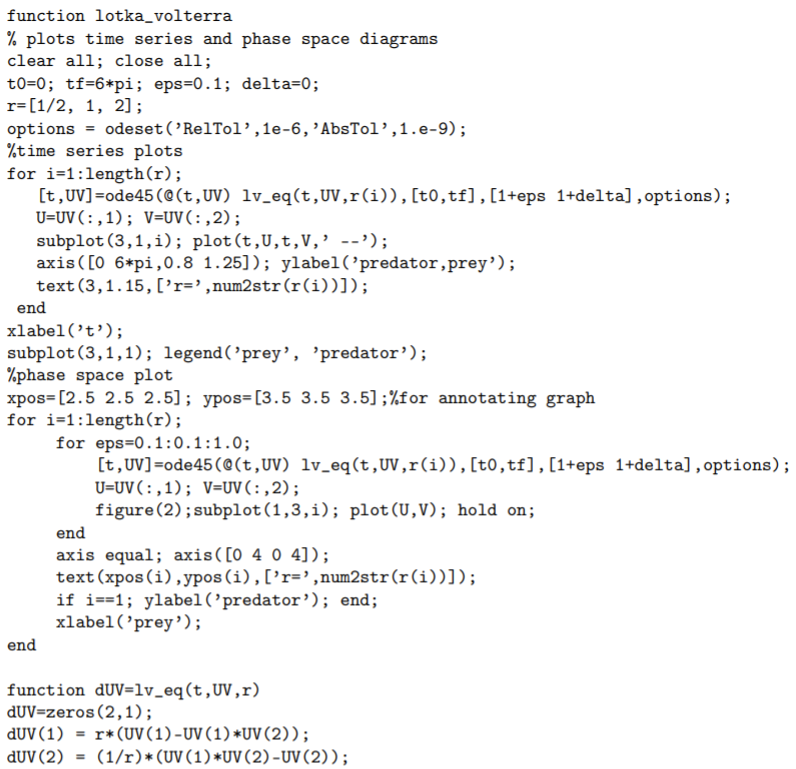
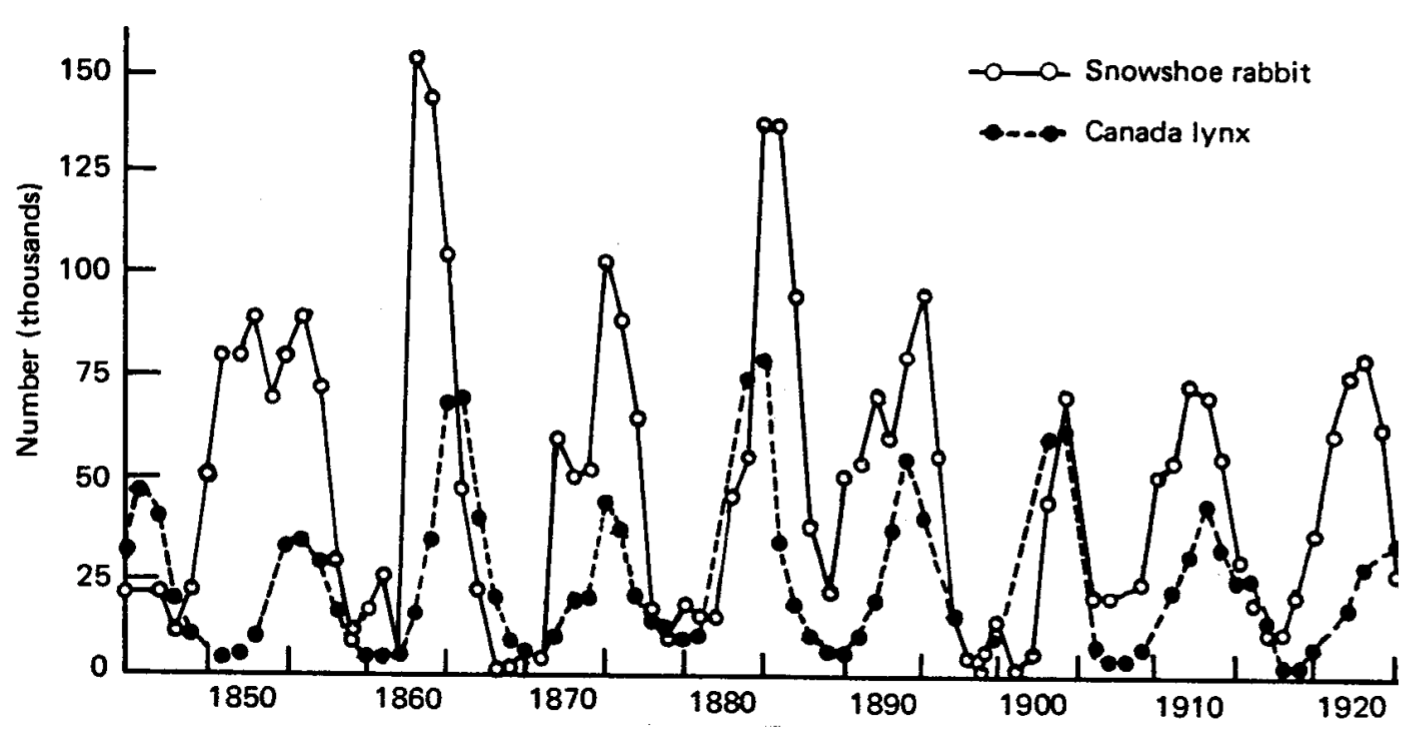
Los registros de comercio de Pelt (Fig. 1.4) de la compañía Hudson Bay de más de un siglo muestran una oscilación casi periódica en el número de liebres y linces atrapados con raquetas de nieve. Con la suposición razonable de que el número registrado de animales atrapados es proporcional a la población animal, estos registros sugieren que las poblaciones depredador-presa, según lo tipificado por la liebre y el lince, pueden oscilar con el tiempo. Lotka y Volterra propusieron independientemente en la década de 1920 un modelo matemático para la dinámica poblacional de un depredador y presa, y estas ecuaciones de Lotka-Volterra depredador-presa se han convertido desde entonces en un modelo icónico de la biología matemática.
Para desarrollar estas ecuaciones, supongamos que una población depredadora se alimenta de una población presa. Suponemos que el número de presas crece exponencialmente en ausencia de depredadores (hay alimento ilimitado disponible para la presa), y que el número de depredadores decae exponencialmente en ausencia de presas (los depredadores deben comer presas o morir de hambre). El contacto entre depredadores y presas aumenta el número de depredadores y disminuye el número de presas.
Dejar\(U(t)\) y\(V(t)\) ser el número de presas y depredadores a la vez\(t\). Para desarrollar un modelo de ecuaciones diferenciales acopladas, consideramos el tamaño de la población en el momento\(t+\Delta t\).
El crecimiento exponencial de presas en ausencia de depredadores y la decadencia exponencial de los depredadores en ausencia de presas pueden ser modelados por los términos lineales habituales. El acoplamiento entre presa y depredador debe modelarse con dos parámetros adicionales. Escribimos los tamaños de la población en el momento\(t+\Delta t\) como
\[\begin{aligned} &U(t+\Delta t)=U(t)+\alpha \Delta t U(t)-\gamma \Delta t U(t) V(t) \\[4pt] &V(t+\Delta t)=V(t)+e \gamma \Delta t U(t) V(t)-\beta \Delta t V(t) \end{aligned} \nonumber \]
Los parámetros\(\alpha\) y\(\beta\) son la tasa de natalidad per cápita promedio de la presa y la tasa de muerte de los depredadores, en ausencia de las otras especies. Los términos de acoplamiento modelan el contacto entre depredadores y presas. El parámetro\(\gamma\) es la fracción de presas capturadas por depredador por unidad de tiempo; el número total de presas capturadas por depredadores durante el tiempo\(\Delta t\) es\(\gamma \Delta t U V\). La presa consumida se convierte luego en depredadores recién nacidos (ver esto como una conversión de biomasa), con factor de conversión\(e\), de modo que el número de depredadores durante el tiempo\(\Delta t\) aumenta en e\ gamma\(\Delta t U V\).
Al convertir estas ecuaciones en ecuaciones diferenciales dejando\(\Delta t \rightarrow 0\), obtenemos las conocidas ecuaciones depredador-presa de Lotka-Volterra
\[\frac{d U}{d t}=\alpha U-\gamma U V, \quad \frac{d V}{d t}=e \gamma U V-\beta V \nonumber \]
Antes de analizar las ecuaciones de Lotka-Volterra, primero revisamos el análisis de estabilidad lineal y de punto fijo aplicado a lo que se llama un sistema autónomo de ecuaciones diferenciales. Por simplicidad, consideramos un sistema de solo dos ecuaciones diferenciales de la forma
\[\dot{x}=f(x, y), \quad \dot{y}=g(x, y), \nonumber \]
aunque nuestros resultados pueden generalizarse a sistemas más grandes. Se dice que el sistema dado por (1.4.2) es autónomo desde entonces\(f\) y\(g\) no dependen explícitamente de la variable independiente\(t\). Los puntos fijos de este sistema se determinan estableciendo\(\dot{x}=\dot{y}=0\) y resolviendo para\(x\) y\(y\). Supongamos que un punto fijo es\(\left(x_{*}, y_{*}\right)\). Para determinar su estabilidad lineal, consideramos condiciones iniciales para\((x, y)\) cerca del punto fijo con pequeñas perturbaciones independientes en ambos sentidos, es decir,\(x(0)=x_{*}+\epsilon(0), y(0)=\)\(y_{*}+\delta(0)\). Si la perturbación inicial crece en el tiempo, decimos que el punto fijo es inestable; si decae, decimos que el punto fijo es estable. En consecuencia, permitimos
\[x(t)=x_{*}+\epsilon(t), \quad y(t)=y_{*}+\delta(t), \nonumber \]
y sustituir\((1.4.3)\) en\((1.4.2)\) para determinar la dependencia del tiempo de\(\epsilon\)\(x_{*}\) y\(\delta .\) Desde y\(y_{*}\) son constantes, tenemos
\[\dot{\epsilon}=f\left(x_{*}+\epsilon, y_{*}+\delta\right), \quad \dot{\delta}=g\left(x_{*}+\epsilon, y_{*}+\delta\right) \nonumber \]
El análisis de estabilidad lineal procede asumiendo que las perturbaciones iniciales\(\epsilon(0)\) y\(\delta(0)\) son lo suficientemente pequeñas como para truncar la expansión bidimensional de la serie Taylor de\(f\) y\(\epsilon=\delta=0\) a\(g\) punto de primer orden en \(\epsilon\)y\(\delta\). Obsérvese que en general, la serie bidimensional Taylor de una función\(F(x, y)\) sobre el origen viene dada por
\[\begin{aligned} F(x, y)=F(0,0)+x F_{x}(0,0) &+y F_{y}(0,0) \\[4pt] &+\frac{1}{2}\left[x^{2} F_{x x}(0,0)+2 x y F_{x y}(0,0)+y^{2} F_{y y}(0,0)\right]+\ldots \end{aligned} \nonumber \]
donde los términos en la expansión puedan recordarse exigiendo que todas las derivadas parciales de la serie coincidan con la de\(F(x, y)\) en el origen. Ahora Taylor-series expandimos\(f\left(x_{*}+\epsilon, y_{*}+\delta\right)\) y\(g\left(x_{*}+\epsilon, y_{*}+\delta\right)\) sobre\((\epsilon, \delta)=(0,0)\). Los términos constantes desaparecen ya que\(\left(x_{*}, y_{*}\right)\) es un punto fijo, y descuidamos todos los términos con órdenes superiores a\(\epsilon\) y\(\delta\). Por lo tanto,
\[\dot{\epsilon}=\epsilon f_{x}\left(x_{*}, y_{*}\right)+\delta f_{y}\left(x_{*}, y_{*}\right), \quad \dot{\delta}=\epsilon g_{x}\left(x_{*}, y_{*}\right)+\delta g_{y}\left(x_{*}, y_{*}\right), \nonumber \]
que puede escribirse en forma de matriz como
\[\frac{d}{d t}\left(\begin{array}{l} \epsilon \\[4pt] \delta \end{array}\right)=\left(\begin{array}{ll} f_{x}^{*} & f_{y}^{*} \\[4pt] g_{x}^{*} & g_{y}^{*} \end{array}\right)\left(\begin{array}{l} \epsilon \\[4pt] \delta \end{array}\right) \nonumber \]
donde\(f_{x}^{*}=f_{x}\left(x_{*}, y_{*}\right)\), etc. La ecuación (1.4.6) es un sistema de oda lineal, y su solución procede asumiendo la forma
\[\left(\begin{array}{l} \epsilon \\[4pt] \delta \end{array}\right)=e^{\lambda t} \mathbf{v} \nonumber \]
Al sustituir y cancelar\((1.4.6)\)\(e^{\lambda t}\), obtenemos el problema del valor propio del álgebra lineal\((1.4.7)\)
\[\mathrm{J}^{*} \mathbf{v}=\lambda \mathbf{v}, \text { with } \mathrm{J}^{*}=\left(\begin{array}{ll} f_{x}^{*} & f_{y}^{*} \\[4pt] g_{x}^{*} & g_{y}^{*} \end{array}\right) \nonumber \]
donde\(\lambda\) está el valor propio,\(\mathbf{v}\) el vector propio correspondiente y\(\mathrm{J}^{*}\) la matriz jacobiana evaluados en el punto fijo. El valor propio se determina a partir de la ecuación característica
\[\operatorname{det}\left(J^{*}-\lambda I\right)=0 \text {, } \nonumber \]
que para una matriz jacobiana de dos por dos da como resultado una ecuación cuadrática para\(\lambda\). De la forma de la solución\((1.4.7)\), el punto fijo es estable si para todos los valores propios\(\lambda\)\(\operatorname{Re}\{\lambda\}<0\),, e inestable si para al menos uno\(\lambda, \operatorname{Re}\{\lambda\}>0 .\) Aquí\(\operatorname{Re}\{\lambda\}\) significa la parte real del (posiblemente) valor propio complejo \(\lambda\). Ahora reconsideramos las ecuaciones de Lotka-Volterra. Las soluciones de punto fijo se encuentran resolviendo\(\dot{U}=\dot{V}=0\), y tenemos de (1.4.1)
\[U(\alpha-\gamma V)=0, \quad V(e \gamma U-\beta)=0 \nonumber \]
Evidentemente, las únicas dos soluciones posibles son
\[\left(U_{*}, V_{*}\right)=(0,0) \text { or }\left(\frac{\beta}{e \gamma}, \frac{\alpha}{\gamma}\right) . \nonumber \]
El punto fijo trivial\((0,0)\) es inestable ya que la población de presas crece exponencialmente si inicialmente es pequeña. Para determinar la estabilidad del segundo punto fijo, escribimos la ecuación de Lotka-Volterra en la forma
\[\frac{d U}{d t}=F(U, V), \quad \frac{d V}{d t}=G(U, V) \nonumber \]
con
\[F(U, V)=\alpha U-\gamma U V, \quad G(U, V)=e \gamma U V-\beta V \nonumber \]
Las derivadas parciales se computan entonces para ser
\[\begin{array}{ll} F_{U}=\alpha-\gamma V, & F_{V}=-\gamma U \\[4pt] G_{U}=e \gamma V, & G_{V}=e \gamma U-\beta . \end{array} \nonumber \]
El jacobiano en el punto fijo\(\left(U_{*}, V_{*}\right)=(\beta / e \gamma, \alpha / \gamma)\) es
\[J^{*}=\left(\begin{array}{cc} 0 & -\beta / e \\[4pt] e \alpha & 0 \end{array}\right) \nonumber \]
y
\[\begin{aligned} \operatorname{det}\left(\mathrm{J}^{*}-\lambda \mathrm{I}\right) &=\left|\begin{array}{cc} -\lambda & -\beta / e \\[4pt] e \alpha & -\lambda \end{array}\right| \\[4pt] &=\lambda^{2}+\alpha \beta \\[4pt] &=0 \end{aligned} \nonumber \]
tiene las soluciones\(\lambda_{\pm}=\pm i \sqrt{\alpha \beta}\), que son puras imaginarias. Cuando los valores propios del jacobiano dos por dos son puros imaginarios, el punto fijo se llama centro y la perturbación no crece ni decae, sino que oscila. Aquí, la frecuencia angular de oscilación es\(\omega=\sqrt{\alpha \beta}\), y el período de la oscilación es\(2 \pi / \omega\).
Trazamos\(U\) y\(V\) versus\(t\) (trama de series de tiempo) y\(V\) versus\(U\) (retratos de fase) para ver cómo se comportan las soluciones. Para un sistema no lineal de ecuaciones como (1.4.1), se requiere una solución numérica.
Las ecuaciones de Lotka-Volterra tienen cuatro parámetros libres\(\alpha, \beta, \gamma\) y\(e\). Las unidades relevantes aquí son el tiempo, el número de presas y el número de depredadores. El\(\mathrm{Pi}\) teorema de Buckingham predice que la no dimensionalización de las ecuaciones puede reducir el número de parámetros libres en tres a una agrupación manejable y adimensional de parámetros. Elegimos no dimensionalizar el tiempo usando la frecuencia angular de oscilación y el número de presas y depredadores usando sus valores de punto fijo. Con los carets que denotan las variables adimensionales, dejamos
\[\hat{t}=\sqrt{\alpha \beta} t, \quad \hat{U}=U / U_{*}=\frac{e \gamma}{\beta} U, \quad \hat{V}=V / V_{*}=\frac{\gamma}{\alpha} V \nonumber \]
La sustitución de (1.4.16) en las ecuaciones de Lotka-Volterra (1.4.1) da como resultado las ecuaciones adimensionales
\[\frac{d \hat{U}}{d \hat{t}}=r(\hat{U}-\hat{U} \hat{V}), \quad \frac{d \hat{V}}{d \hat{t}}=\frac{1}{r}(\hat{U} \hat{V}-\hat{V}) \nonumber \]
con agrupación única adimensional\(r=\sqrt{\alpha / \beta} .\) La especificación de\(r\) junto con las condiciones iniciales determina completamente la solución. Cabe señalar aquí que la solución a largo plazo de las ecuaciones de Lotka-Volterra depende de las condiciones iniciales. Esta dependencia asintótica de las condiciones iniciales suele considerarse un defecto del modelo.
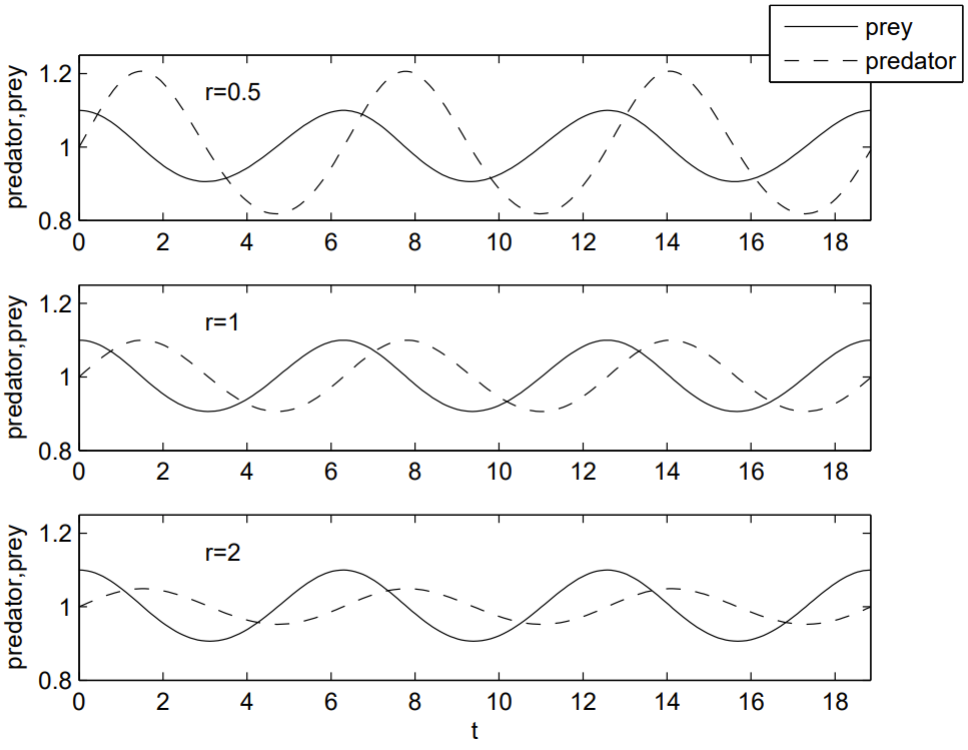
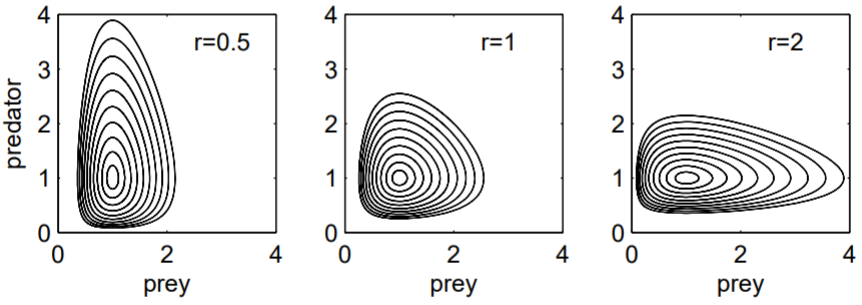
Una solución numérica utiliza la función integrada ode45.m de MATLAB para integrar las ecuaciones diferenciales. El siguiente código produce la Fig. 1.5. Observe cómo la población de depredadores está rezagada con respecto a la población de presas: un aumento en el número de presas resulta en un aumento retrasado en el número de depredadores a medida que los Los retratos de fase muestran claramente la periodicidad de la oscilación. Tenga en cuenta que las curvas se mueven en sentido antihorario: el número de presas aumenta cuando el número de depredadores es mínimo, y el número de presas disminuye cuando el número de depredadores