6.4: Inhibición alostérica

Última actualización
Guardar como PDF

Page ID: 117633

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

El término alosterio proviene de la palabra griega allos, que significa diferente, y estéreos, que significa sólido, y se refiere a una enzima con un sitio de unión regulador separado de su sitio de unión activo. En nuestro modelo de inhibición alostérica, se supone que una molécula inhibidora se une a su propio sitio regulador en la enzima, lo que resulta en una menor afinidad de unión del sustrato a la enzima, o una tasa de conversión reducida de sustrato a producto. Una caricatura de inhibición alostérica debida a una afinidad de unión disminuida se muestra en la Fig. $6.3$.

En general, necesitamos definir tres complejos:$C_{1}$ es el complejo formado a partir de sustrato y enzima;$C_{2}$ de inhibidor y enzima, y;$C_{3}$ a partir de sustrato, inhibidor y enzima. Escribimos las reacciones químicas de la siguiente manera:

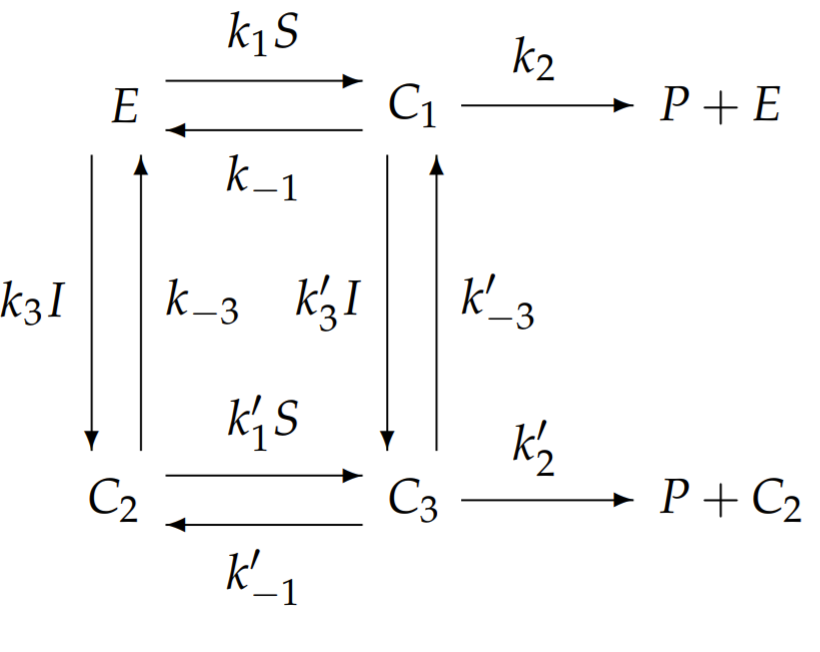
$clipboard_e7c6048933a68c0850cd297b12417b071.png$

El modelo general de inhibición alostérica con diez constantes de velocidad independientes parece demasiado complicado de analizar. Simplificaremos este modelo general a uno con menos constantes de velocidad que aún exhibe las características únicas de la inhibición alostérica. Una simplificación posible pero poco interesante supone que si$I$ se une a$E$, entonces no$S$ lo hace; sin embargo, esto reduce la inhibición alostérica a inhibición competitiva y pierde la esencia de la alostería. En cambio, simplificamos permitiendo que ambos$I$ y se unan simultáneamente$S$ a$E$, pero suponemos que la unión de I impide la conversión del sustrato en producto. Con esta simplificación,$k_{2}^{\prime}=0$. Para reducir aún más el número de constantes de velocidad independientes, asumimos que la unión de$S$ a no$E$ se ve afectada por la presencia ligada de$I$, y la unión de$I$ a no$E$ se ve afectada por el límite presencia de$S$. Estas aproximaciones implican que todas las constantes de velocidad cebadas son iguales a las constantes de velocidad no cebadas correspondientes$k_{1}^{\prime}=k_{1}$, e.g., etc. Con estas simplificaciones, el esquema de la reacción química simplifica a

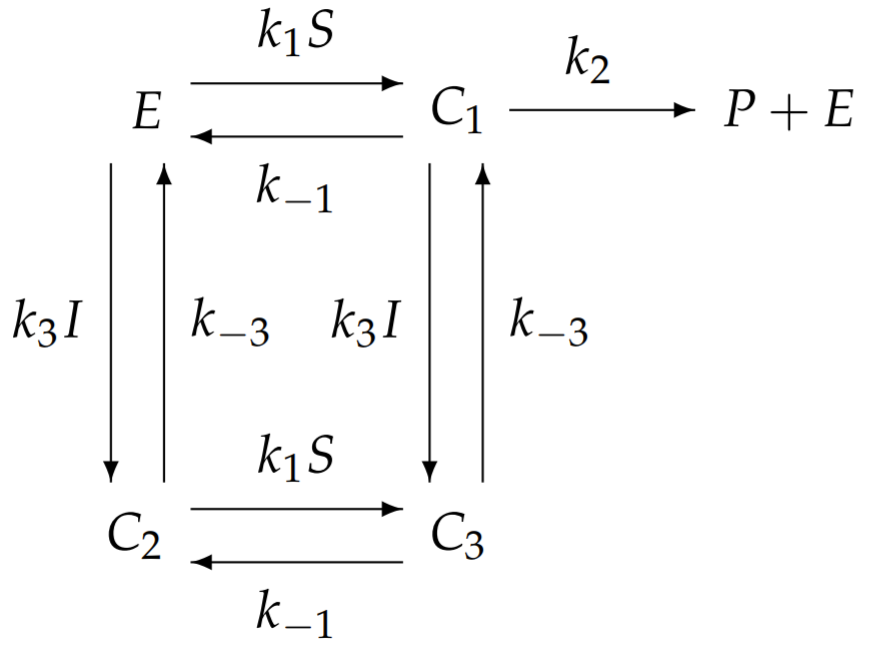
$clipboard_eaf907d6091b64c4a42b2f90c6571d8ac.png$

y ahora sólo hay cinco constantes de tasa independientes. Escribimos las ecuaciones para los complejos usando la ley de acción de masas:

\[\begin{align} &\frac{d C_{1}}{d t}=k_{1} S E+k_{-3} C_{3}-\left(k_{-1}+k_{2}+k_{3} I\right) C_{1} \\[4pt] &\frac{d C_{2}}{d t}=k_{3} I E+k_{-1} C_{3}-\left(k_{-3}+k_{1} S\right) C_{2} \\[4pt] &\frac{d C_{3}}{d t}=k_{3} I C_{1}+k_{1} S C_{2}-\left(k_{-1}+k_{-3}\right) C_{3} \end{align} \nonumber \]

mientras que la velocidad de reacción viene dada por

\[\frac{d P}{d t}=k_{2} C_{1} \nonumber \]

Nuevamente, se conserva tanto la enzima libre como la ligada, así que eso$E=E_{0}-C_{1}-C_{2}-C_{3}$. Con la aproximación de cuasi-equilibrio$\dot{C}_{1}=\dot{C}_{2}=\dot{C}_{3}=0$, obtenemos un sistema de tres ecuaciones y tres incógnitas:$C_{1}, C_{2}$ y$C_{3} .$ A pesar de nuestras simplificaciones, la solución analítica para la velocidad de reacción sigue siendo desordenada (ver Keener & Sneyd, referenciado en el final del capítulo) y no especialmente esclarecedor. Aquí omitimos el resultado analítico completo y determinamos solo la velocidad máxima de reacción.

La velocidad máxima de reacción$V_{m}^{\prime}$ para la reacción alostérico-inhibida se define como la derivada en el tiempo de la concentración del producto cuando la reacción está saturada con sustrato; es decir,

\[\begin{aligned} V_{m}^{\prime} &=\lim _{S \rightarrow \infty} d P / d t \\[4pt] &=k_{2} \lim _{S \rightarrow \infty} C_{1} \end{aligned} \nonumber \]

Con la saturación del sustrato, cada enzima tendrá su sitio de unión al sustrato ocupado. Las enzimas están unidas con solo sustrato en el complejo$C_{1}$, o unidas entre sí con sustrato e inhibidor en el complejo$C_{3}$. En consecuencia, el esquema de la reacción química con saturación del sustrato simplifica a

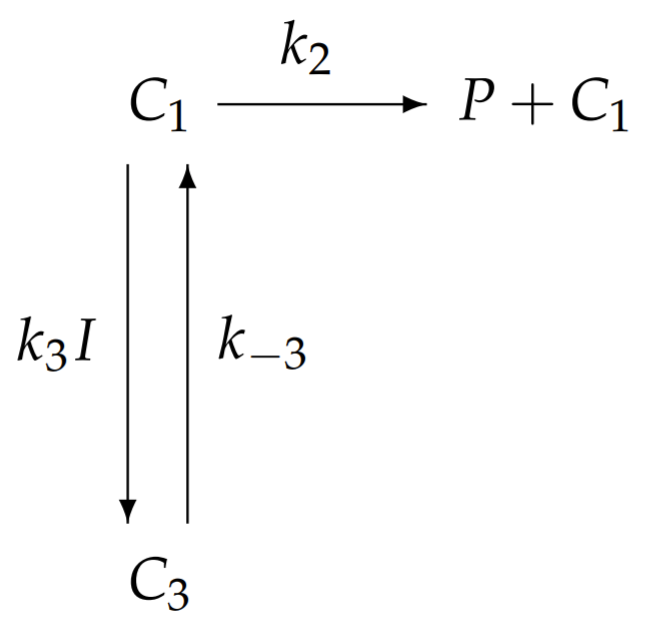
$clipboard_e440294fbb66b8045d534adf265bfc3fd.png$

Por lo tanto, las ecuaciones para$C_{1}$ y$C_{3}$ con la saturación del sustrato están dadas por

\[\begin{align} \frac{d C_{1}}{d t} &=k_{-3} C_{3}-k_{3} I C_{1} \\[4pt] \frac{d C_{3}}{d t} &=k_{3} I C_{1}-k_{-3} C_{3} \end{align} \nonumber \]

y la aproximación de cuasi-equilibrio produce la ecuación independiente única

\[\begin{align} \nonumber C_{3} &=\left(k_{3} / k_{-3}\right) I C_{1} \\[4pt] &=\left(I / K_{i}\right) C_{1} \end{align} \nonumber \]

con$K_{i}=k_{-3} / k_{3}$ como antes. La ecuación que expresa la conservación de la enzima viene dada por$E_{0}=C_{1}+C_{3}$. Esta ley de conservación, junto con$(6.4.7)$, nos permite resolver por$C_{1}$:

\[C_{1}=\frac{E_{0}}{1+I / K_{i}} \nonumber \]

Por lo tanto, la velocidad máxima de reacción para la reacción alostérico-inhibida viene dada por

\[\begin{aligned} V_{m}^{\prime} &=\frac{k_{2} E_{0}}{1+I / K_{i}} \\[4pt] &=\frac{V_{m}}{1+I / K_{i}} \end{aligned} \nonumber \]

donde$V_{m}$ es la velocidad máxima de reacción tanto de la reacción desinhibida como de la reacción inhibida competitiva. Se ve así que el inhibidor alostérico reduce la velocidad máxima de la reacción desinhibida por el factor$\left(1+I / K_{i}\right)$, que puede ser grande si la concentración de inhibidor alostérico es sustancial.