6.5: Cooperatividad

Las enzimas y otros complejos proteicos pueden tener múltiples sitios de unión, y cuando un sustrato se une a uno de estos sitios, los otros sitios pueden volverse más activos. Un ejemplo bien estudiado es la unión de la molécula de oxígeno a la proteína hemlobina. La hemoglobina puede unirse a cuatro moléculas de\(\mathrm{O}_{2}\), y cuando tres moléculas están unidas, la cuarta molécula tiene una mayor afinidad por la unión. A esto lo llamamos cooperatividad.

Modelaremos la cooperatividad asumiendo que una enzima tiene dos sitios de unión separados pero indistinguibles para un sustrato\(S\). Por ejemplo, la enzima puede

Figura 6.4: Cooperatividad.

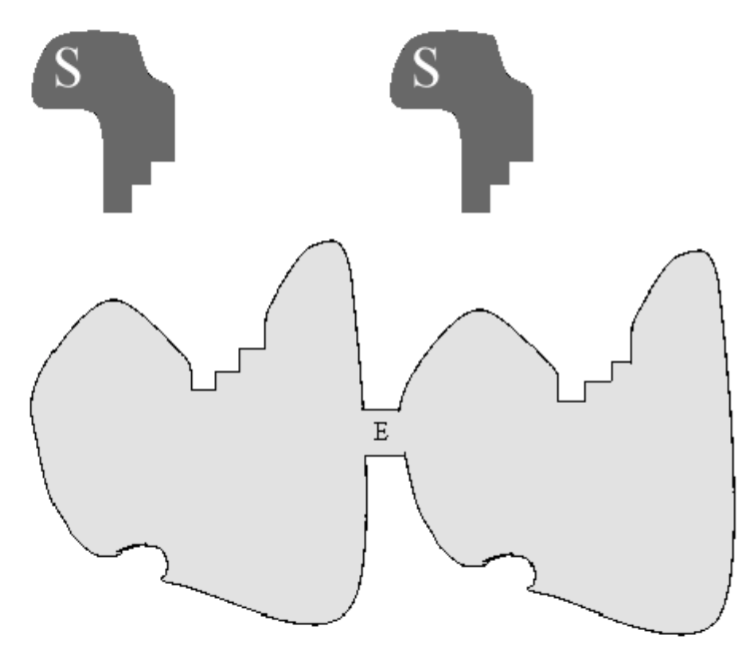
ser un dímero proteico, compuesto por dos subproteínas idénticas con sitios de unión idénticos para\(S\). Una caricatura de esta enzima se muestra en la Fig. 6.4. Debido a que los dos sitios de unión son indistinguibles, necesitamos considerar solo dos complejos:\(C_{1}\) y\(C_{2}\), con enzima unida a una o dos moléculas de sustrato, respectivamente. Cuando la enzima exhibe cooperatividad, la unión de la segunda molécula sustrato tiene una constante de velocidad mayor que la unión de la primera. Por lo tanto, consideramos la siguiente reacción:

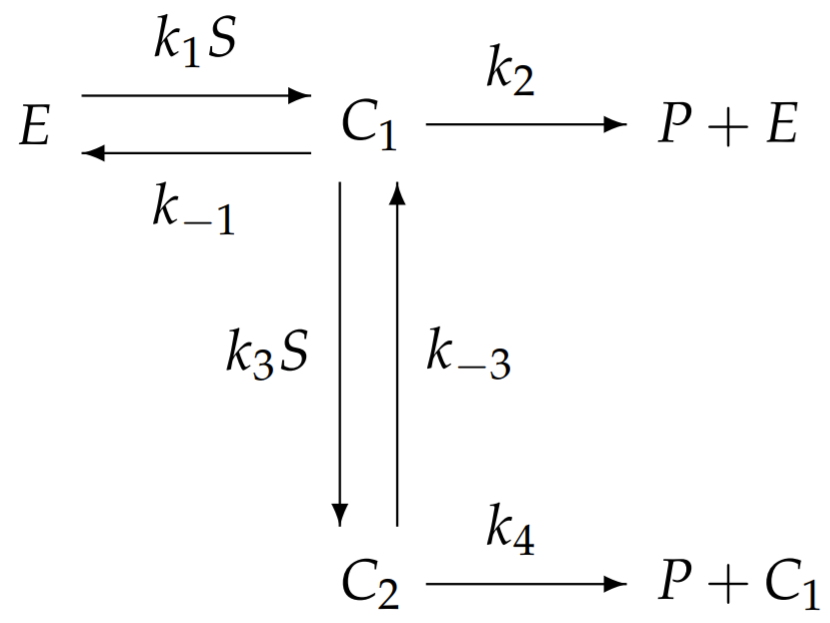
donde la cooperatividad supone eso\(k_{1} \ll k_{3}\). Aplicación de la ley de acción masiva da como resultado

\[\begin{aligned} \frac{d C_{1}}{d t} &=k_{1} S E+\left(k_{-3}+k_{4}\right) C_{2}-\left(k_{-1}+k_{2}+k_{3} S\right) C_{1} \\[4pt] \frac{d C_{2}}{d t} &=k_{3} S C_{1}-\left(k_{-3}+k_{4}\right) C_{2} \end{aligned} \nonumber \]

La aplicación de la aproximación cuasi-equilibrio\(\dot{C}_{1}=\dot{C}_{2}=0\) y la ley de conservación\(E_{0}=E+C_{1}+C_{2}\) da como resultado el siguiente sistema de dos ecuaciones y dos incógnitas:

\[\begin{align} \left(k_{-1}+k_{2}+\left(k_{1}+k_{3}\right) S\right) C_{1}-\left(k_{-3}+k_{4}-k_{1} S\right) C_{2} &=k_{1} E_{0} S, \\[4pt] k_{3} S C_{1}-\left(k_{-3}+k_{4}\right) C_{2} &=0 . \end{align} \nonumber \]

Dividimos\((6.5.1)\) por\(k_{1}\) y\((6.5.2)\) por\(k_{3}\) y definimos

\[K_{1}=\frac{k_{-1}+k_{2}}{k_{1}}, \quad K_{2}=\frac{k_{-3}+k_{4}}{k_{3}}, \quad \epsilon=k_{1} / k_{3} \nonumber \]

para obtener

\[\begin{align} \left(\epsilon K_{1}+(1+\epsilon) S\right) C_{1}-\left(K_{2}-\epsilon S\right) C_{2} &=\epsilon E_{0} S, \\[4pt] S C_{1}-K_{2} C_{2} &=0 . \end{align} \nonumber \]

Podemos restar (6.5.5) de (6.5.4) y cancelar\(\epsilon\) para obtener

\[\left(K_{1}+S\right) C_{1}+S C_{2}=E_{0} S . \nonumber \]

Las ecuaciones (6.5.5) y (6.5.6) se pueden resolver para\(C_{1}\) y\(C_{2}\):

\[\begin{align} C_{1} &=\frac{K_{2} E_{0} S}{K_{1} K_{2}+K_{2} S+S^{2}} \\[4pt] C_{2} &=\frac{E_{0} S^{2}}{K_{1} K_{2}+K_{2} S+S^{2}} \end{align} \nonumber \]

de modo que la velocidad de reacción viene dada por

\[\begin{align} \frac{d P}{d t} &=k_{2} C_{1}+k_{4} C_{2} \\[4pt] &=\frac{\left(k_{2} K_{2}+k_{4} S\right) E_{0} S}{K_{1} K_{2}+K_{2} S+S^{2}} \end{align} \nonumber \]

Para iluminar este resultado, consideramos dos casos limitantes: (i) no cooperatividad, donde los sitios activos actúan de manera independiente para que cada dímero proteico, digamos, pueda considerarse como dos monómeros proteicos independientes; (ii) fuerte cooperatividad, donde la unión del segundo sustrato tiene una constante de velocidad mucho mayor que la encuadernación de la primera.

Sitios activos independientes

Figura 6.5: La velocidad\(d P / d t\) de reacción en función del sustrato\(S\). Se muestran las soluciones a la ecuación de Hill con\(V_{m}=1, K_{m}=1\), y para\(n=1,2\).

Por lo tanto, para sitios activos independientes, la velocidad de reacción se vuelve

\[\begin{aligned} \frac{d P}{d t} &=\frac{\left(2 k_{2} K_{m}+2 k_{2} S\right) E_{0} S}{K_{m}^{2}+2 K_{m} S+S^{2}} \\[4pt] &=\frac{2 k_{2} E_{0} S}{K_{m}+S} \end{aligned} \nonumber \]

La velocidad de reacción para una enzima proteína dímera compuesta por monómeros idénticos independientes es simplemente el doble que la de una enzima de proteína monomérica, un resultado intuitivamente obvio.

Fuerte cooperatividad

Ahora asumimos que después de que el primer sustrato se una a la enzima, el segundo sustrato se une mucho más fácilmente, de manera que eso\(k_{1} \ll k_{3}\). En consecuencia, el número de enzimas unidas a una sola molécula de sustrato debe ser mucho menor que el número unido a dos moléculas de sustrato, lo que resulta en\(C_{1} \ll C_{2}\). Dividiendo (6.5.7) por (6.5.8), esta desigualdad se convierte

\[\frac{C_{1}}{C_{2}}=\frac{K_{2}}{S} \ll 1 . \nonumber \]

Dividiendo el numerador y denominador de\((6.5.9)\) por\(S^{2}\), tenemos

\[\frac{d P}{d t}=\frac{\left(k_{2} K_{2} / S+k_{4}\right) E_{0}}{\left(K_{1} / S\right)\left(K_{2} / S\right)+\left(K_{2} / S\right)+1} . \nonumber \]

Para tomar el límite de esta expresión como\(K_{2} / S \rightarrow 0\), nos fijamos en\(K_{2} / S=0\) todas partes excepto en el primer término en el denominador, ya que\(K_{1} / S\) es inversamente proporcional a\(k_{1}\) y puede llegar al infinito en este límite. Tomando el límite y multiplicando el numerador y denominador por\(S^{2}\),

\[\frac{d P}{d t}=\frac{k_{4} E_{0} S^{2}}{K_{1} K_{2}+S^{2}} \nonumber \]

Aquí, la velocidad máxima de reacción es\(V_{m}=k_{4} E_{0}\), y la constante MichaelisMenten modificada es\(K_{m}=\sqrt{K_{1} K_{2}}\), de modo que

\[\frac{d P}{d t}=\frac{V_{m} S^{2}}{K_{m}^{2}+S^{2}} \nonumber \]

En bioquímica, esta velocidad de reacción se generaliza a

\[\frac{d P}{d t}=\frac{V_{m} S^{n}}{K_{m}^{n}+S^{n}} \nonumber \]

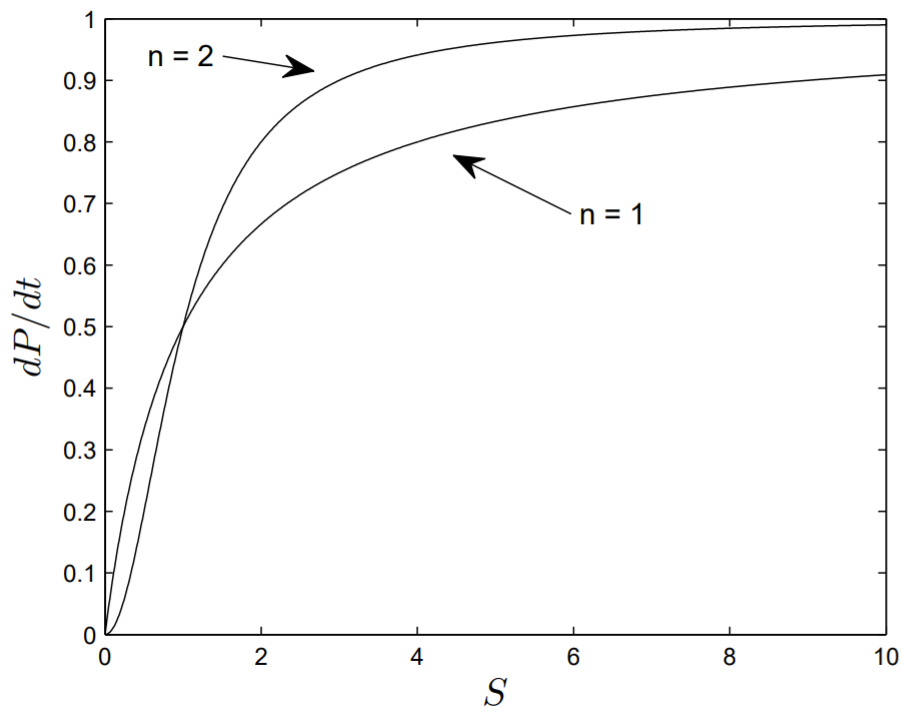
conocida como la ecuación de Hill, y variando\(n\) se utiliza para ajustar los datos experimentales.

En la Fig. \(6.5\), hemos trazado la velocidad de reacción\(d P / d t\) versus\(S\) la obtenida de la ecuación de Hill con\(n=1\) o 2. Al dibujar la figura, hemos tomado ambos\(V_{m}\) e\(K_{m}\) iguales a la unidad. Es evidente que con\(n\) el aumento de la velocidad de reacción se satura más rápidamente a su valor máximo.