7.1: Pendiente de una línea

Última actualización
Guardar como PDF

Page ID: 112454

Victoria Dominguez, Cristian Martinez, & Sanaa Saykali
Citrus College via ASCCC Open Educational Resources Initiative

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Recuerde que los pares ordenados se pueden graficar como puntos en el plano de coordenadas rectangulares. A través de dos puntos distintos, graficar una línea recta,$l$.

Para describir la línea$l$ algebraicamente, primero considere la pendiente de una fórmula de línea.

Definición: Pendiente de una línea

La pendiente$m$ de una línea$l$ que pasa por puntos$(x_1, y_1)$ y$(x_2, y_2)$ es

\[m = \dfrac{\text{rise}}{\text{run}} = \dfrac{y_2 − y_1}{x_2 − x_1} \text{ where } x_2 \neq x_1 \nonumber \]

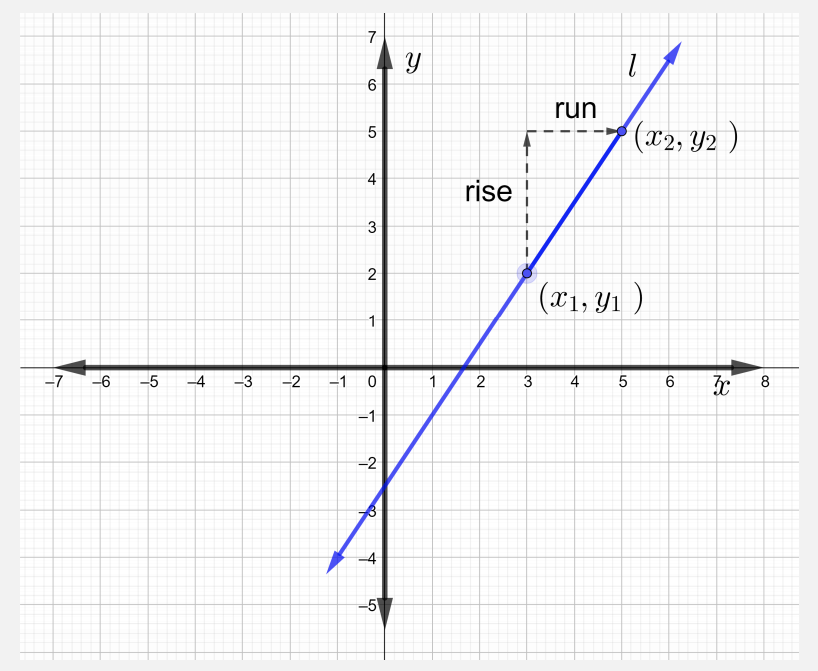
$clipboard_ef5b30d9d90d175767e807356eeeb09d5.png$

Ejemplo 7.1.1

Encuentra la pendiente de la línea en la siguiente figura.

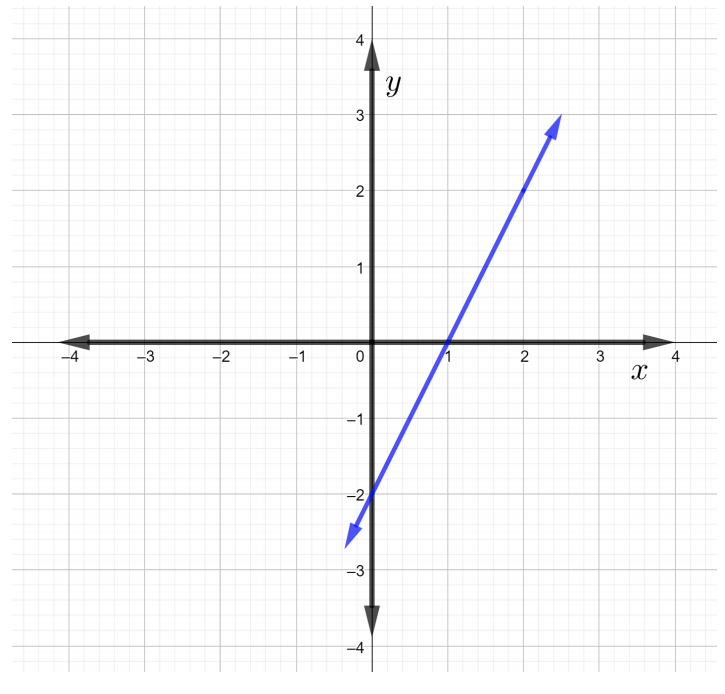
$clipboard_e363ff7b3bb533d1487bf37ba2e55050d.png$

Solución

Por la definición anterior de la pendiente de la fórmula de línea, la pendiente de la línea se puede escribir como$m = \dfrac{\text{rise}}{\text{run}}$. Comience eligiendo dos puntos cualquiera,$P$ y$Q$, en la línea. Elige punto$P$ para ser$(2, 2)$ y punto$Q$ para ser$(1, 0)$.

Comenzando en el punto$Q$, subir a punto$P$ contando cuadrados de$2$ cuadrícula ascendentes, lo que significa$\text{rise} = 2$. Ahora, para llegar al punto$P$,$\text{run}$$1$ cuadricula cuadrada a la derecha, lo que significa que$\text{run} = 1$, como se muestra en la siguiente figura.

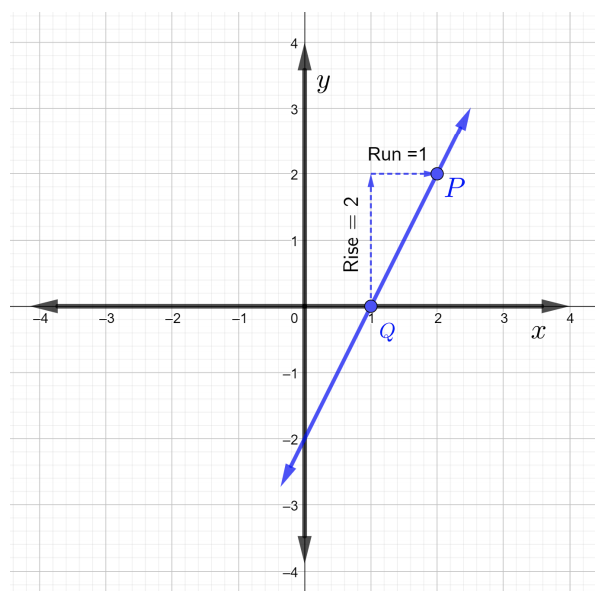
$clipboard_eb782dfab92d784f98c38e932215ff3af.png$

Por lo tanto,

$\begin{array} &&m = \dfrac{\text{rise}}{\text{run}} &\text{slope of a line formula} \\ &= \dfrac{2}{1} &\text{rise \(2$y ejecutar$1$}\\ &= 2\ end {array}\)

Por lo tanto, la pendiente de la línea en la figura es$m = 2$.

Ejemplo 7.1.2

Encuentra la pendiente de la línea que se muestra en la siguiente figura.

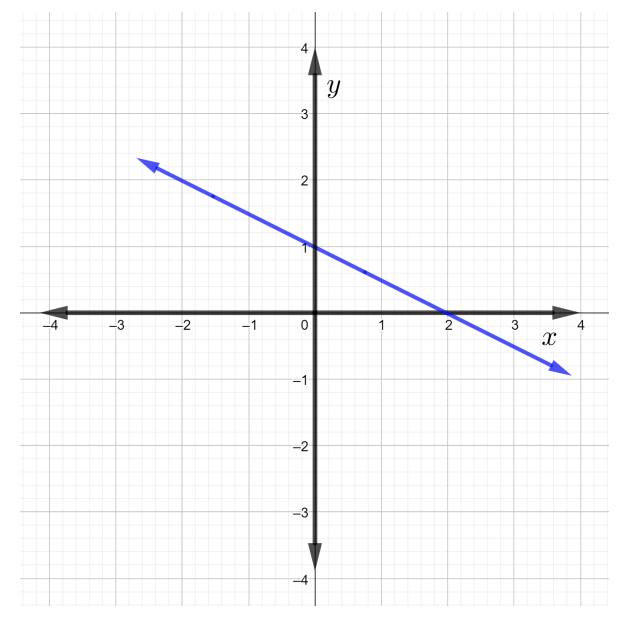
$clipboard_e19cd2064387c2c10ad2af63dccc6440d.png$

Solución

Similar a Ejemplo$1$, comience por elegir dos puntos cualesquiera,$P$ y$Q$, en la línea.

Nota: Dado que se puede elegir cualquier$2$ punto de la línea, será más fácil elegir los dos puntos que son enteros. Esos puntos se encuentran en la línea y también en la intersección de dos líneas de rejilla. Por ejemplo, en la figura será más fácil elegir cualquiera de los dos puntos siguientes en la línea dada:$(2, 0)$,$(0, 1)$,$(4, −1)$,$(6, −2)$,$(−4, 3)$,$(−6, 4)$, y así sucesivamente...

La pendiente es la misma para cualquiera de dos puntos$P$ y$Q$ en la línea. Elige punto$P_1$ para ser$(0, 1)$ y punto$Q_1$ para ser$(2, 0)$. Comenzando en el punto$P_1$, llegar al punto$Q_1$ corriendo primero los cuadrados de la$2$ cuadrícula hacia la derecha, lo que significa que el$\text{run} = 2$. Ahora, para llegar al$Q_1$ recuento de puntos$1$ cuadriculado a la baja. Observe, que el$\text{rise} = -1$ que significa bajar la$1$ unidad como se muestra en la siguiente figura.

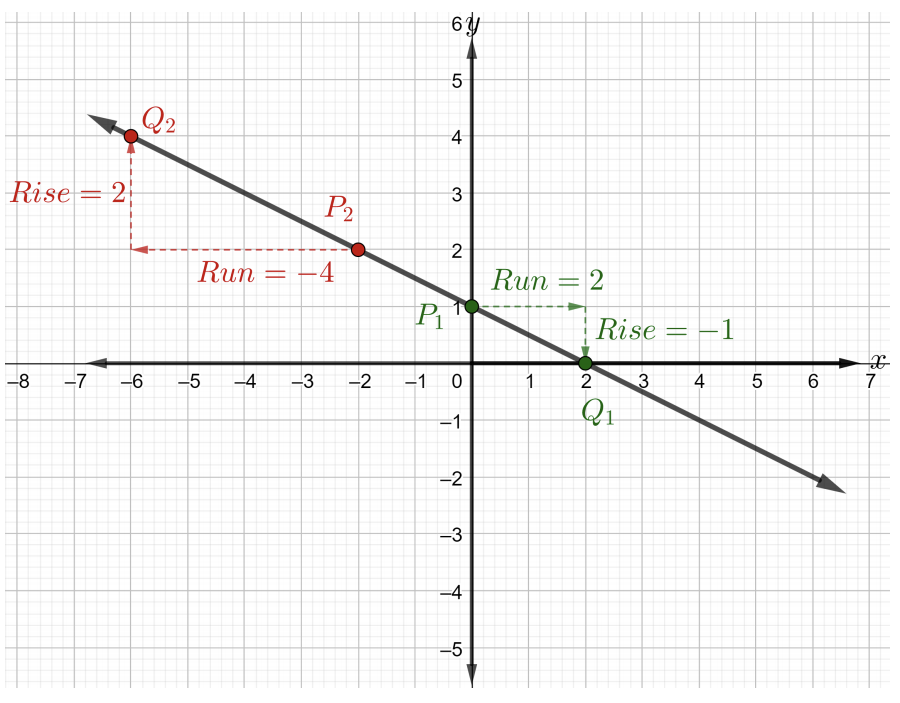
$clipboard_eae1964d11eb4f5c0410a5ca79250683d.png$

$\begin{array} &&m = \dfrac{\text{rise}}{\text{run}} &\text{slope of a line formula} \\ &= \dfrac{−1}{2} &\text{rise = \(-1$y ejecutar =$2$}\ end {array}\)

Por lo tanto, la pendiente de la línea en la figura anterior es$m = −\dfrac{1}{2}$.

Ahora, elija punto$P_2$ para ser$(-2, 2)$ y punto$Q_2$ para ser$(-6, 4)$ como se muestra en la figura anterior. Comenzando en puntos$P_2$, llegar al punto$Q_2$ por primera vez corriendo cuadrados de$4$ cuadrícula hacia la izquierda, lo que significa que el$\text{run} = -4$. Ahora, para llegar a puntos$Q_2$ contar cuadrados de$2$ cuadrícula ascendentes. Así, el$\text{rise} = 2$. La pendiente es$m = \dfrac{2}{−4} = −\dfrac{1}{2}$. Observe que la pendiente es la misma independientemente de qué$2$ puntos consideremos en una línea dada.

Ejemplo 7.1.3

Encuentra la pendiente de la línea que atraviesa$(3, 2)$ y$(4, 4)$ usando la fórmula del talud. Grafica la línea que pasa por los puntos dados.

Nota: El orden en que se etiqueten los puntos no hará diferencia en la pendiente de una fórmula de línea siempre y cuando haya consistencia.

Solución

Vamos$(x_1, y_1) = (3, 2)$ y$(x_2, y_2) = (4, 4)$ luego,

$\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{slope of a line formula} \\ &= \dfrac{4 − 2}{4 − 3} & \\ &= \dfrac{2}{1} &\text{rise \(= 2$y ejecutar$= 1$}\\ &= 2 &\ end {array}\)

Por lo tanto, la pendiente de la línea que pasa por puntos$(3, 2)$ y$(4, 4)$ es$m = 2$. La línea que pasa por los puntos dados es como se muestra en la siguiente figura.

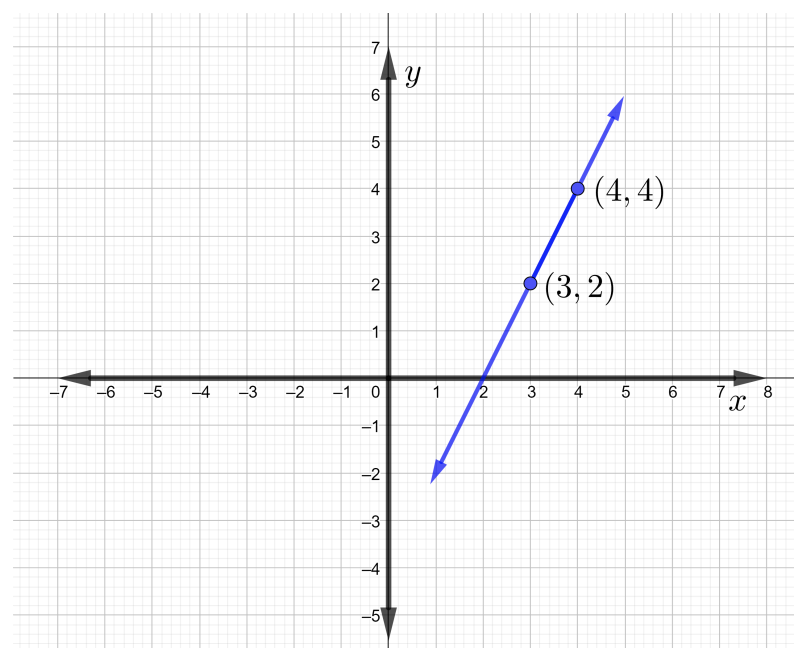
$clipboard_e274e9e3b46b3eff108909c81ba819a08.png$

Observe que cuando la línea sube de izquierda a derecha, la línea tiene una pendiente positiva.

Ejemplo 7.1.4

Encuentra la pendiente de la línea que pasa por los puntos$(−1, 2)$ y$(3, −4)$. Trazar los puntos y graficar la línea.

Solución

Vamos$(x_1, y_1) = (-1, 2)$ y$(x_2, y_2) = (3, -4)$ luego,

$\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{slope of a line formula} \\ &= \dfrac{-4 − 2}{3 − (-1)} & \\ &= \dfrac{-6}{4} &\text{Simplify} \\ &= -\dfrac{3}{2} & \end{array}$

Definición: Pendiente Negativa

Ahora, para graficar la línea a través de los puntos dados, primero trazar los dos puntos, luego dibujar una línea recta a través de ellos, como se muestra en la Figura siguiente.

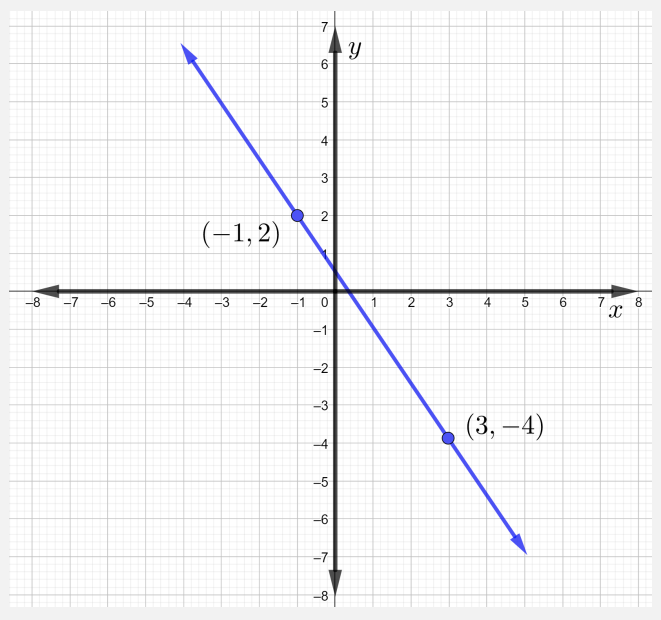
$clipboard_e8812e320ff1738607c4d0a7b47b2cb52.png$

Observe que cuando la línea cae de izquierda a derecha, la línea tiene una pendiente negativa.

Ejercicio 7.1.1

Encuentra las pendientes de cada línea en la gráfica en Problemas$1$ a través de$4$

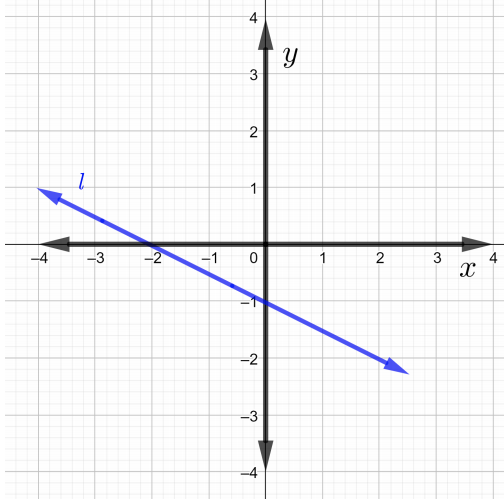
$clipboard_e2069ff2347366ba7a41bdc2ce9b3e73f.png$

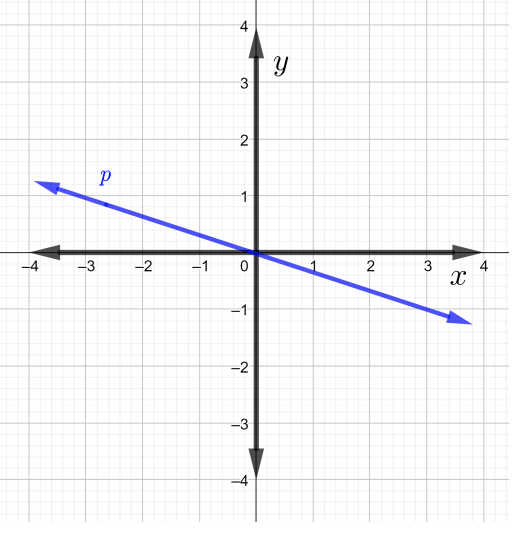
$clipboard_eef225bb0ac28f968c0341273544f4c10.png$

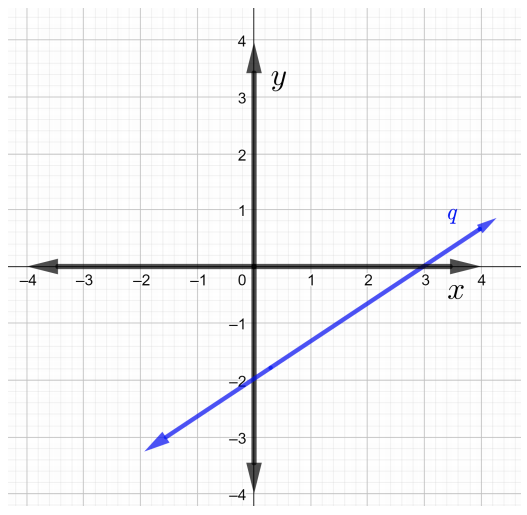
$clipboard_e529b1bdc19f0e169b699c7c48d14cd9f.png$

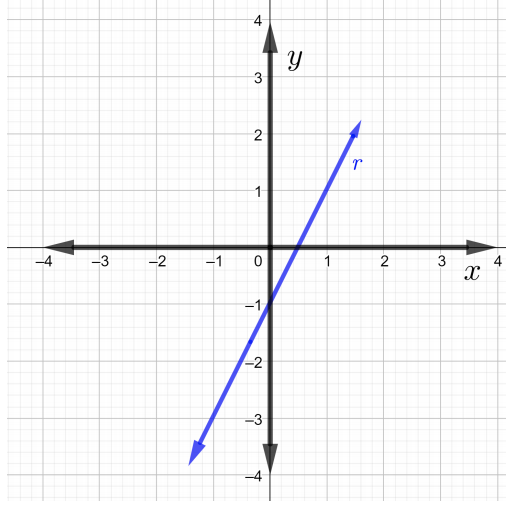
$clipboard_e02a729d98b0411466737730bd716df03.png$

Ejercicio 7.1.2

Encuentra la pendiente de la línea que pasa por los puntos dados en Problemas$5$ a través$7$.

$(−3, 5)$y$(4, −5)$
$(2, 5)$y$(0, −1)$
$(4, 1)$y$(0, 0)$