1.2: Diagramas de Venn
- Page ID
- 113208
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
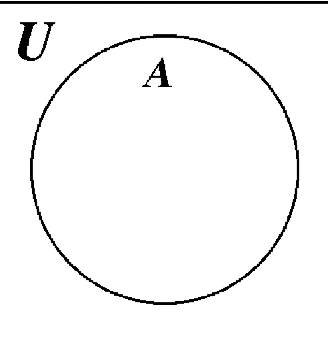
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\) Este es un diagrama de Venn usando solo un conjunto, A
Este es un diagrama de Venn usando solo un conjunto, A Este es un diagrama de Venn a continuación usando dos conjuntos, A y B.
Este es un diagrama de Venn a continuación usando dos conjuntos, A y B.
Estudie los diagramas de Venn en esta y en las siguientes páginas. Se necesita mucha práctica para sombrear o identificar regiones de diagramas de Venn. Tenga en cuenta que puede ser necesario sombrear varios diagramas de práctica a lo largo del camino antes de llegar al resultado final.
Sombra diagramas de Venn para representar conjuntos. Estaremos haciendo algunos diagramas de Venn muy fáciles y básicos así como varios diagramas de Venn involucrados y complicados.
Para encontrar la intersección de dos conjuntos, puede intentar sombrear una región en una dirección determinada y otra región en una dirección diferente. Entonces mirarías donde esos sombreados se superponen. Esa superposición sería la intersección.
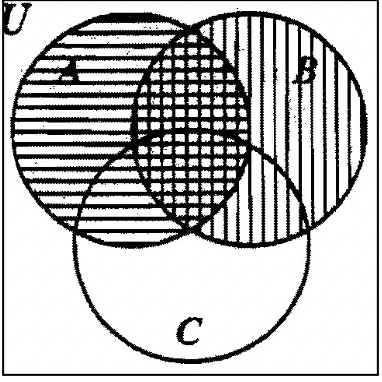
Por ejemplo, para visualizar\(A \cap B\), sombrear A con líneas horizontales y B con líneas verticales. Entonces el solapamiento es\(A \cap B\). El diagrama de la izquierda sería un primer paso para obtener la respuesta. La parte sombreada en el diagrama de la derecha muestra la respuesta final.
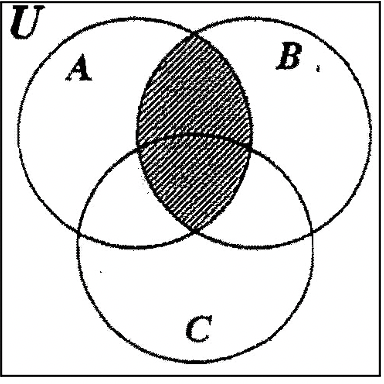
Aquí tienes dos problemas para que pruebes. Solo sombra en la respuesta final para cada ejercicio.
Sombra la región que representa\(A \cap C\)
Sombra la región que representa\(B \cap C\)
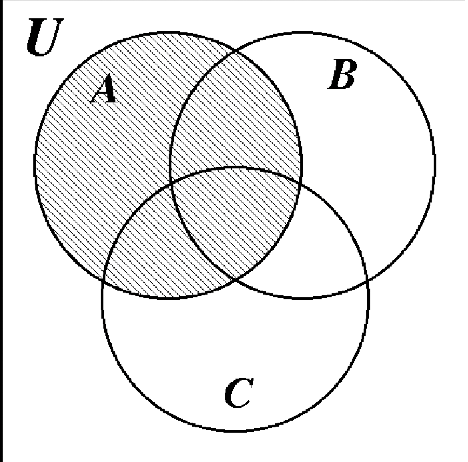
Para sombrear la unión de dos conjuntos, sombree cada región completamente o sombree ambas regiones en la misma dirección. Así, para encontrar la unión de A y B, sombrear todo A y todo B.

La respuesta final está representada por el área sombreada en el diagrama a la derecha.
Aquí tienes dos problemas para que pruebes. Solo sombra en la respuesta final para cada ejercicio.
Sombra la región que representa\(A \cup C\)

Sombra la región que representa\(B \cup C\)

Para el complemento de una región, sombree todo fuera de la región dada. Se puede pensar en ello como sombrear todo excepto esa región. En el diagrama de Venn a la izquierda, el área sombreada representa A. En el diagrama de Venn a la derecha, el área sombreada representa.
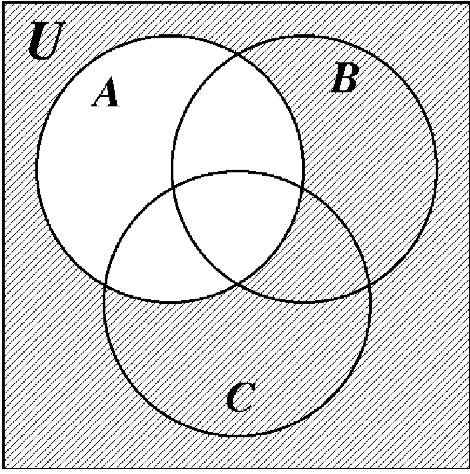
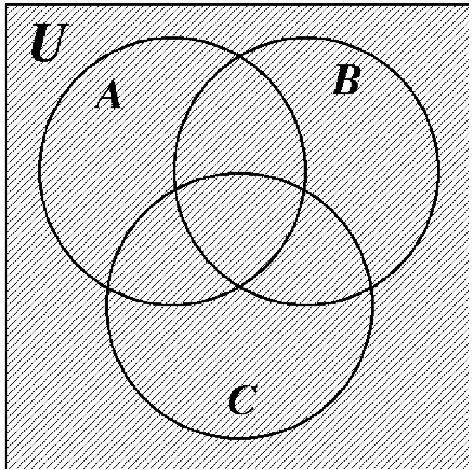
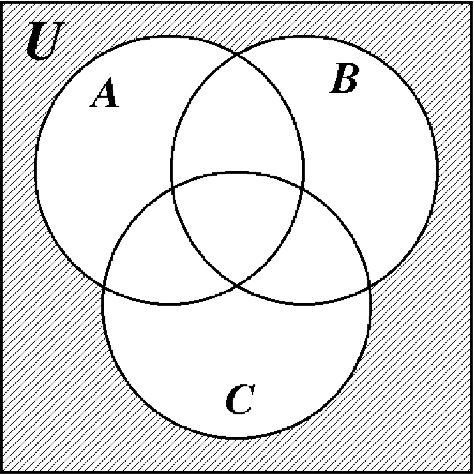
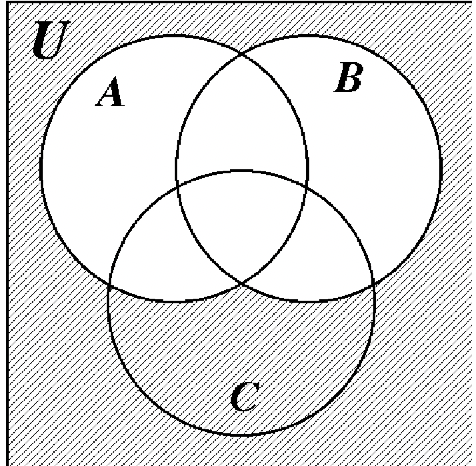
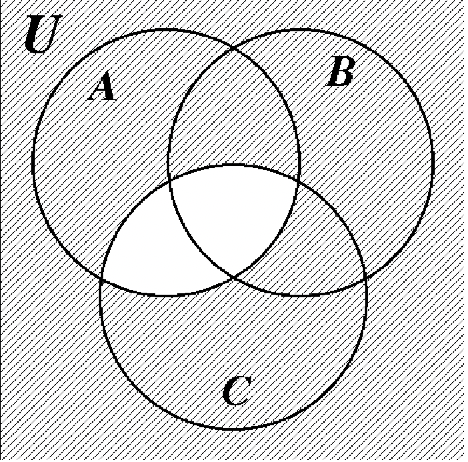
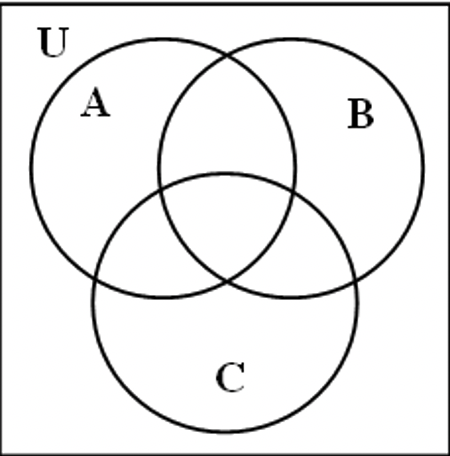
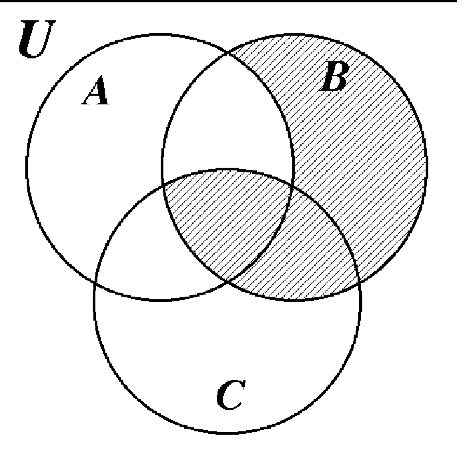
Mucha gente está confundida acerca de qué parte del diagrama de Venn representa al universo, U. El universo es todo el diagrama de Venn, incluyendo los conjuntos A, B y C. Los tres diagramas de Venn en la página siguiente ilustran las diferencias entre U,\(U^{c}\) y\((A \cup B \cup C)^{c}\). Anote cuidadosamente estas diferencias.
 U U |
 \((A \cup B \cup C)^{c}\) \((A \cup B \cup C)^{c}\) |
 \(U^{c}\) \(U^{c}\) |
Por lo general, los paréntesis son necesarios para indicar qué operación debe realizarse primero. Si solo hay unión o intersección involucrada, esto no es necesario como en (A\(\cup\) B\(\cup\) C)\(^{c}\) anterior. Convénzase de que ((A\(\cup\) B)\(\cup\) C) =\(\cup\) (A (B\(\cup\) C)). De igual manera, convencerse del hecho análogo para la intersección realizando los siguientes pasos. En el primer diagrama de Venn a continuación, sombra A\(\cap\) B con líneas horizontales y sombra C con líneas verticales. Entonces, el solapamiento es ((A\(\cap\) B)\(\cap\) C). En el segundo diagrama de Venn, sombra A con líneas inclinadas hacia la derecha y B\(\cup\) C con líneas inclinadas hacia la izquierda. Entonces el solapamiento es (A\(\cap\) (B\(\cap\) C)). Verifica para ver que la respuesta final, la superposición en este caso, es la misma para ambos. Sombra la respuesta final en el tercer diagrama de Venn.
a. (A\(\cap\) B)\(\cap\) C

b. (A\(\cup\) (B\(\cup\) C))

c. Sombra la respuesta final aquí.

Ahora, es el momento de que pruebes algunos diagramas más por tu cuenta. Puede tomar más de un paso averiguar la respuesta. Es posible que primero tengas que hacer dibujos preliminares en papel rascar. Los sombreados que muestres aquí deberían ser solo la respuesta final, pero deberías poder explicar y apoyar cómo llegaste a tu respuesta. Compara tus respuestas con otras personas de tu clase y asegúrate de que se llegue a un consenso sobre la respuesta correcta. Haz esto para todos los diagramas de Venn a lo largo de este conjunto de ejercicios. Sombra en la región que representa lo que está escrito encima de cada uno de los seis diagramas de Venn en la siguiente página. Tenga en cuenta que en los casos que involucren más de una operación, es necesario usar paréntesis y seguir el orden de las operaciones. Los ejercicios 10 y 11 ilustran por qué esto es necesario.
B\(^{c}\)

(C\(\cap\) A)\(^{c}\)

(B\(\cup\) C)\(^{c}\)

(A\(\cap\) B\(\cap\) C)\(^{c}\)

(A\(\cap\) B)\(\cap\) C

(A\(\cap\) (B\(\cap\) C)

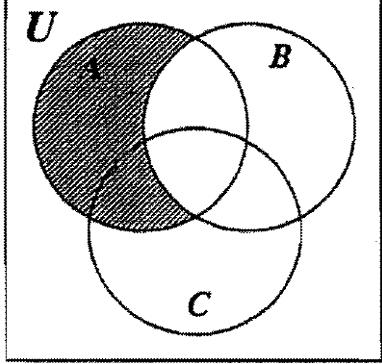
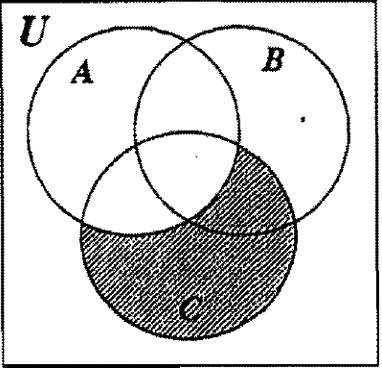
Para la diferencia, sombree la región que viene antes del signo de diferencia (—) pero no incluya ni sombree ninguna parte de la región que siga al signo de diferencia. El Venn de la izquierda representa A—B y el de la derecha representa C — A.
Aquí tienes dos problemas para que pruebes. Solo sombra en la respuesta final para cada ejercicio.
Sombra la región que representa A — C

Sombra la región que representa B — C

Estudia los siguientes diagramas de Venn. Asegúrate de entender cómo obtener las respuestas.
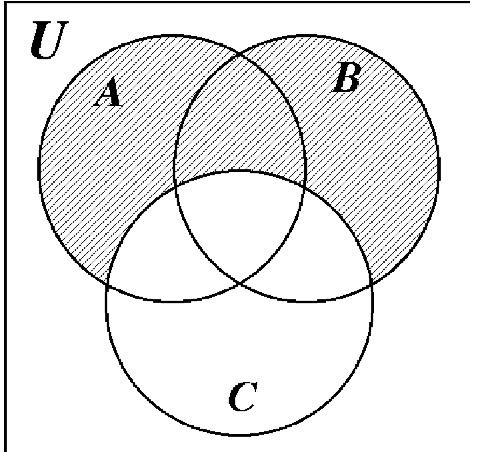
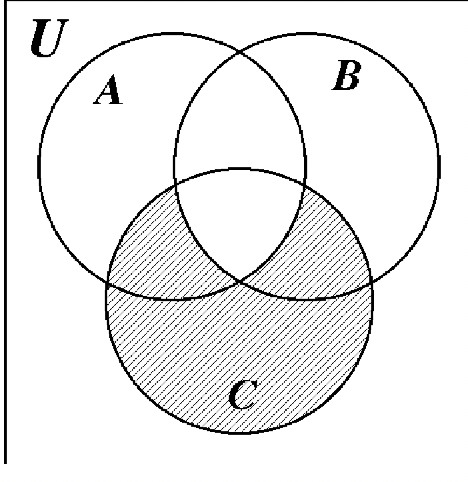
Es tu turno de sombra en la región que representa lo que está escrito encima de cada diagrama.
(A\(\cap\) C) — B
B — (A\(\cap\) C)

(A — C) \(\cup\)(B — A)

Supongamos que quería encontrar ((C — A)\(\cap\) B)\(^{c}\). Esto probablemente tomaría algunos pasos para obtener la respuesta. Un enfoque para encontrar el sombreado correcto es notar que la respuesta final es el complemento de (C — A)\(\cap\) B. Eso significa que primero tendríamos que averiguar cómo era (C — A)\(\cap\) B. Para ello, notamos que esta es la intersección de dos cosas C — A y B. En el diagrama de Venn en blanco a la izquierda de abajo, sombra C — A con líneas horizontales y B con líneas verticales. El solapamiento sería la intersección. La superposición en su dibujo debe coincidir con el sombreado que se muestra en el diagrama de Venn en el medio. ¿Lo hace? El último paso sería entonces tomar el complemento del sombreado que se muestra en el diagrama del medio. Esto se muestra en el diagrama de Venn en el extremo derecho. Entonces, se necesitó dibujar tres Venns para llegar a la respuesta final para este problema. Alguien más podría hacerlo en menos pasos mientras que alguien más podría dar más pasos.
 |
(C — A)\(\cap\) B 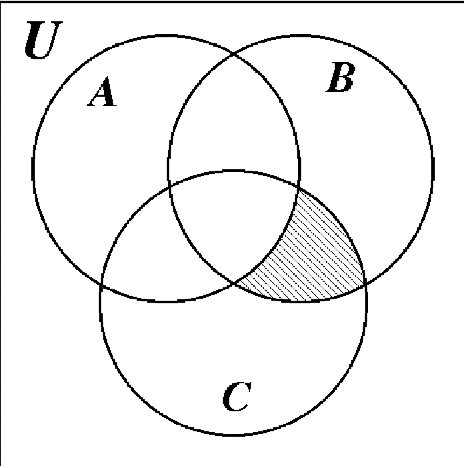 |
((C — A) \(\cap\)B)\(^{c}\) 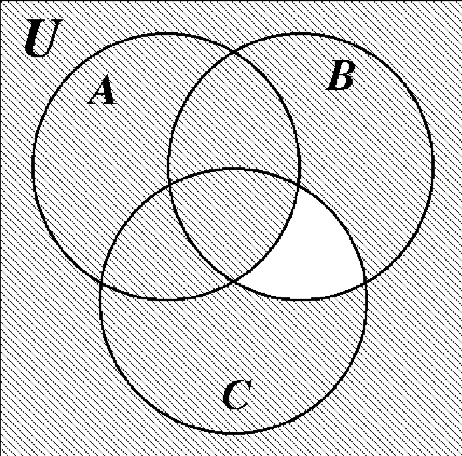 |
Como se mencionó anteriormente, se necesita mucha práctica para ser bueno sombreando diagramas de Venn. Es aún más complicado mirar un diagrama de Venn y describirlo, De hecho, suele haber más de una forma de describir un diagrama de Venn. Por ejemplo, el sombreado para ((C — A)\(\cap\) B) que\(^{c}\) se muestra en la página anterior es el mismo que para ((C\(\cap\) B) — A)\(^{c}\). ¿Qué significa esto? Estamos tan acostumbrados a tener solo una respuesta correcta. Bueno, considera si alguien te pidió que escribieras un problema aritmético para el que la respuesta fue 2. Habría infinitamente muchas posibilidades. Por ejemplo, 5 - 3 o 1 + 1 o 10/5 serían todas respuestas aceptables. Concedido, este tipo de preguntas en una prueba sería más difícil para un maestro calificar porque la respuesta de cada alumno tendría que ser verificada para ver si funcionaría. No hay una respuesta de palmadita. Lo mismo ocurre si un maestro te pide que mires un sombreado de un diagrama de Venn y lo describas. Por otro lado, si se da una descripción y se le pide que sombree el diagrama de Venn, solo hay un sombreado correcto. Es muy parecido a que se le pida que compute un problema aritmético. ¡La respuesta a 10 - 8 es 2 y esa es la única respuesta aceptable!
El punto de todo esto es que dominar los sombreados de los diagramas de Venn y las descripciones de los diagramas de Venn mirando los sombreados requiere mucha, mucha y mucha práctica. Date tiempo de sobra para estudiar y trabajar en ellos y lograrás esta hazaña!!!
En las siguientes páginas, se le pide que sombree varios diagramas de Venn de uno, dos y tres conjuntos. Siguen los sombreados correctos. Asegúrate de probar estos problemas en serio. Asegúrate de poder explicar los pasos involucrados para llegar al sombreado correcto. Después de dominar los sombreados, vea si puede mirar un diagrama de Venn sombreado y llegar a una descripción precisa. Nuevamente, recuerde que hay más de una manera de describir un diagrama de Venn dado.
Estos diagramas de Venn serán útiles a la hora de estudiar para una prueba. Regresa y practica dibujar los mismos diagramas de Venn más tarde. Usa las respuestas para ver si puedes describirlas mirando la imagen. Por supuesto, recuerda que tu descripción podría no coincidir exactamente ya que hay más de una forma de describir cualquier diagrama de Venn dado. Si tu descripción es diferente, asegúrate de seguir los pasos de sombrear un Venn con tu descripción y ver si tu sombreado realmente coincide con el diagrama de Venn que estabas tratando de describir.
Aquí hay algunos diagramas sombreados de Venn. A ver si puedes mirar los sombreados y llegar a una descripción. He puesto algunas posibles respuestas al final de esta página.
 |
 |
 |
Aquí hay algunas descripciones posibles para los diagramas de Venn anteriores:
| (C — B)\(^{c}\) | (A\(\cup\) C)\(^{c}\) | (A\(\cap\) C)\(^{c}\) |
Sombra la región que representa lo que está escrito encima de cada uno de los diagramas de Venn establecidos uno y dos a continuación. Es posible que primero deba dibujar dibujos preliminares para algunos de ellos.
A
\(A^{c}\)

U

\(U^{c}\)

A\(\cap\) B

A\(\cup\) B

\(A \cup B^{c}\)

\((A \cap B)^{c}\)

\((A \cup B)^{c}\)

(A\ B)\(\cup\) (B\ A)

\(A^{c} \cup B^{c}\)

\(A^{c} \cap B^{c}\)

\((A \cup B)^{c} \cup (A \cap B)\)

B

B - A

\(B^{c}\)

Sombra la región que representa lo que está escrito encima de cada uno de los diagramas de Venn establecidos uno y dos a continuación. Es posible que primero deba dibujar dibujos preliminares para algunos de ellos.
(A\(\cap\) B) — C

(C\(\cup\) B) — A

(A\(\cap\) B)\(\cup\) C

(A\(\cup\) B)\(\cap\) C

A\(^{c}\) — B

A\(\cap\) B\(\cap\) C) — B

B — (A\(\cup\) C)

C — (A\(\cap\) B)

(B — A)\(\cap\) (B — C)

(B — A)\(\cup\) (B — C)

(A\(\cup\) B)\(^{c}\)

A\(^{c}\) \(\cap\)B\(^{c}\)

A\(^{c}\) — B\(^{c}\)

(C — B)\(^{c}\)

(B\(^{c}\) \(\cap\)C) — A

(A — (B\(\cup\) C))\(\cup\) (B — (A\(\cup\) C))\(\cup\) (C — (A\(\cup\) B))

(A\(\cap\) C)\(^{c}\)

(A\(\cap\) B) — C)\(\cap\) (C — A)

A\(^{c}\) \(\cup\)C\(^{c}\)

B\(\cap\) (C\(\cup\) A\(^{c}\))

Aquí están los sombreados correctos a los ejercicios en las páginas anteriores. Después de dominar estos sombreados, invierta el proceso mirando los sombreados en esta página e intente describirlos. Se necesita práctica y paciencia y recuerda que puede haber más de una manera de describir algunos de estos. De hecho, muchas veces verás que hay una manera más sencilla de describirlos que estaba en el ejercicio original!!
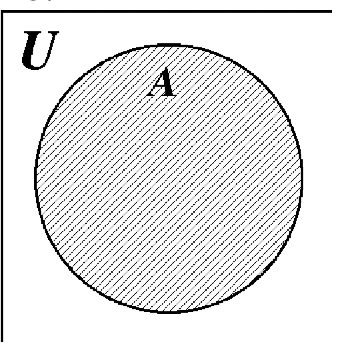 18.
18.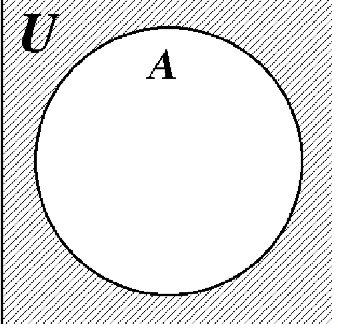 19.
19.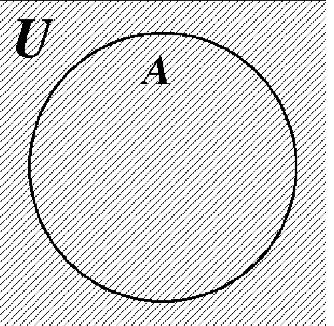 20.
20.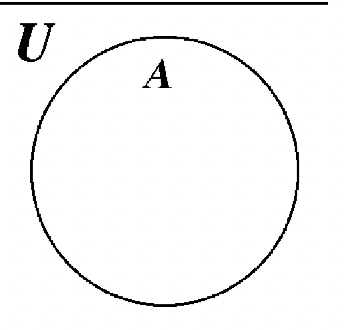 21.
21.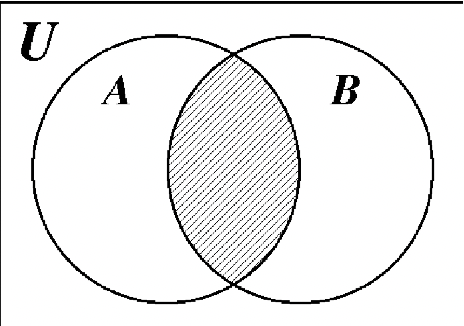 22.
22.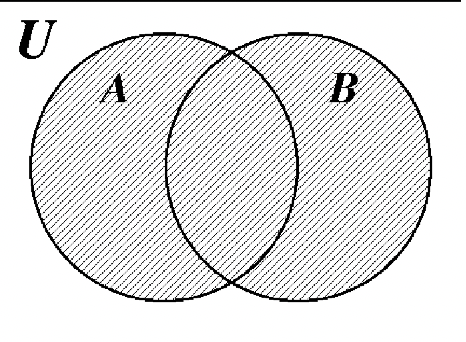 23.
23.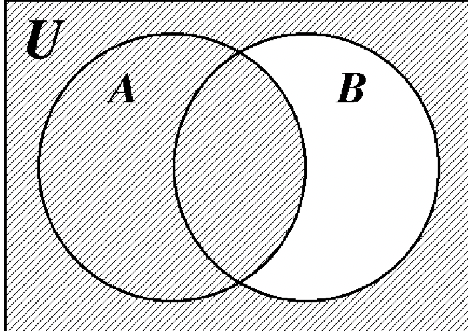 24.
24.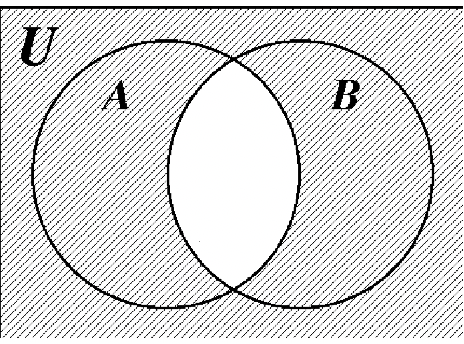 25.
25. 26.
26. 27.
27. 28.
28. 29.
29. 30.
30. 31.
31. 32.
32. 33.
33.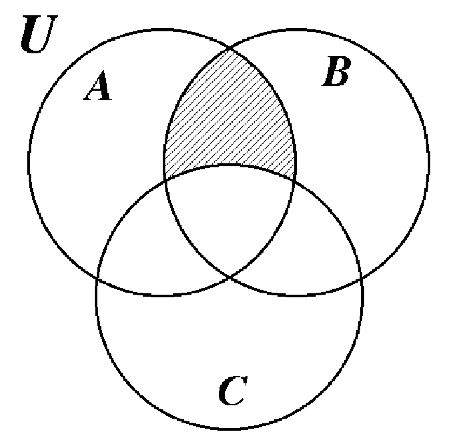 34.
34.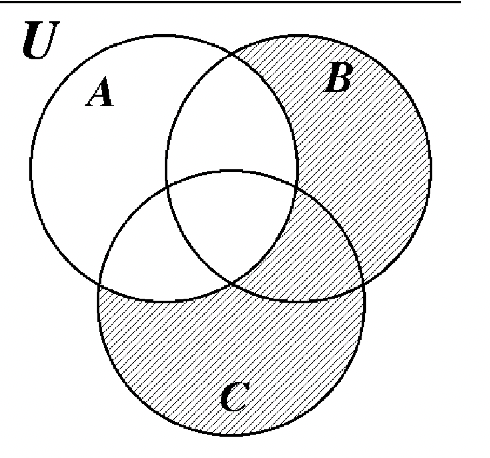 35.
35.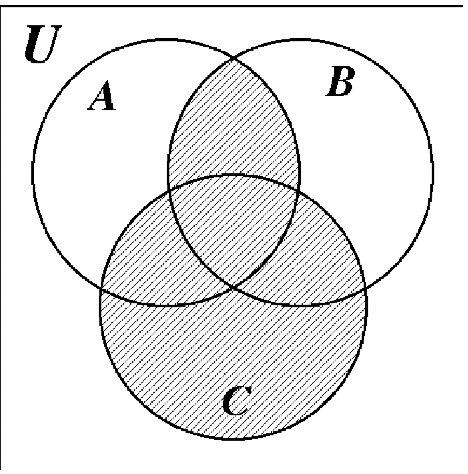 36.
36.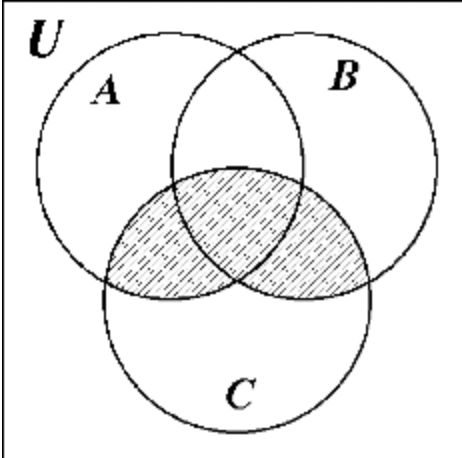 37.
37. 38.
38. 39. Nada está sombreado.
39. Nada está sombreado.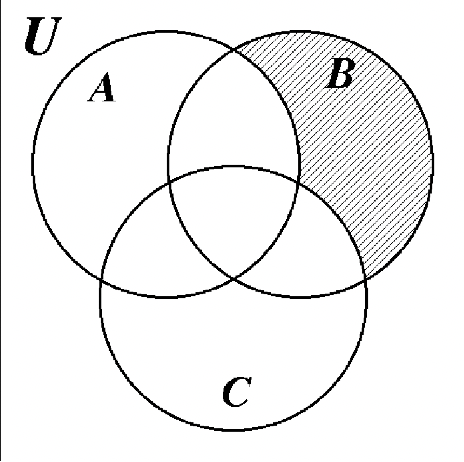 40.
40.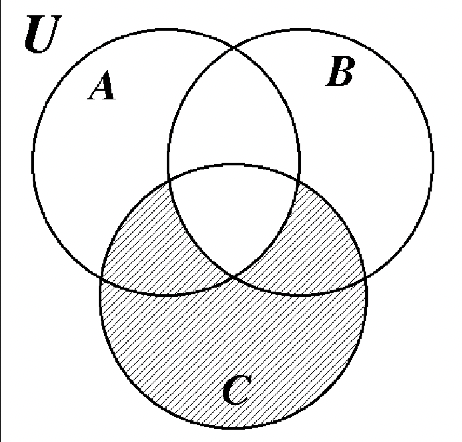 41.
41.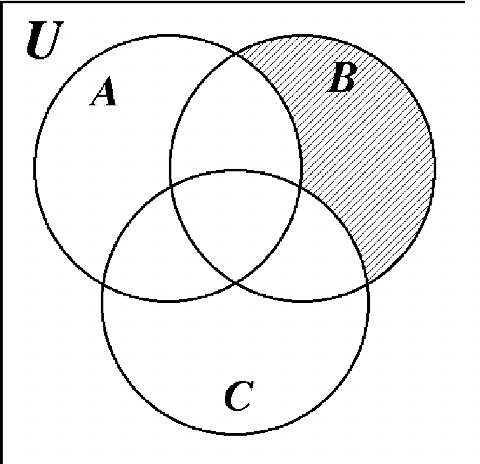 42.
42.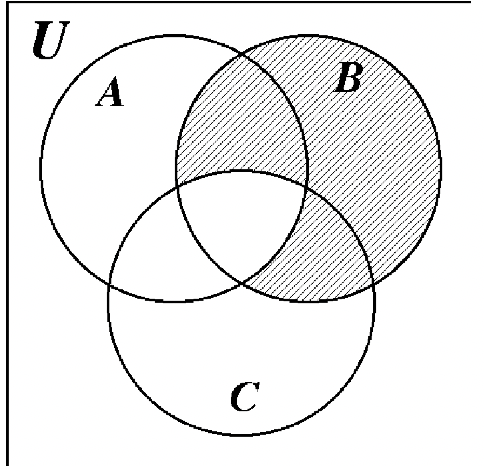 43.
43.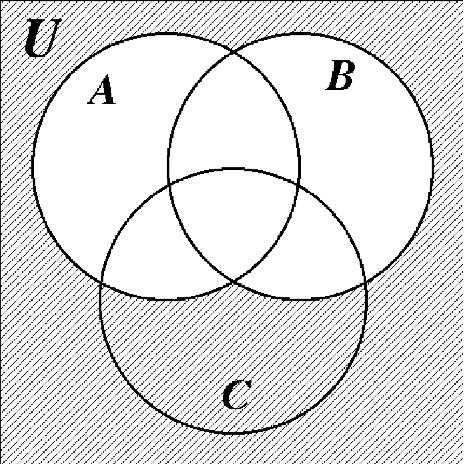 44.
44.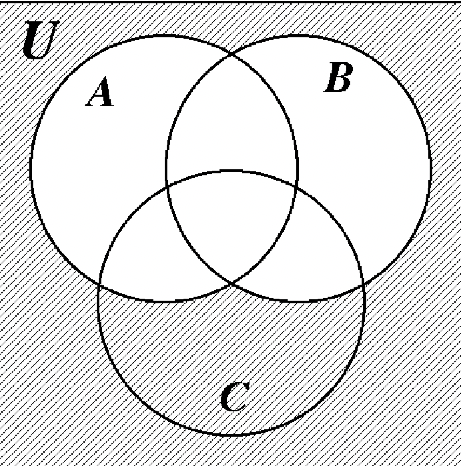 45.
45. 46.
46.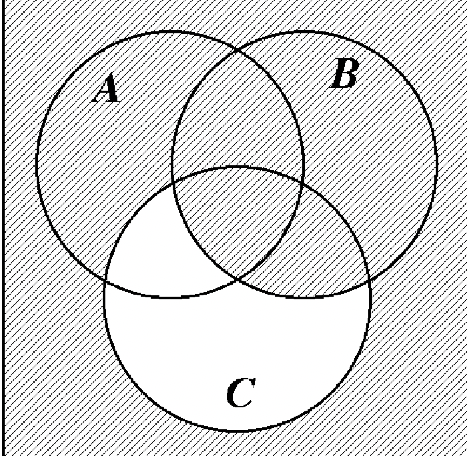 47.
47.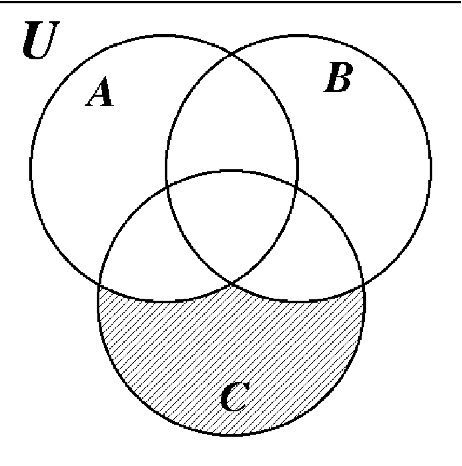 48.
48.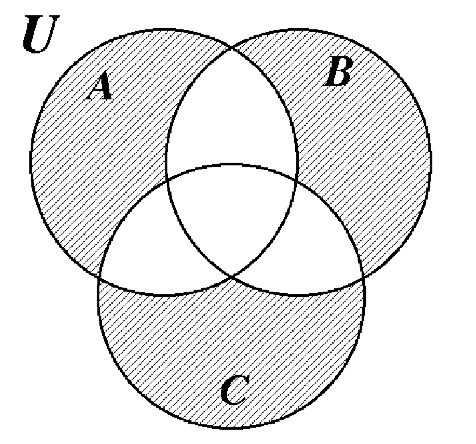 49.
49.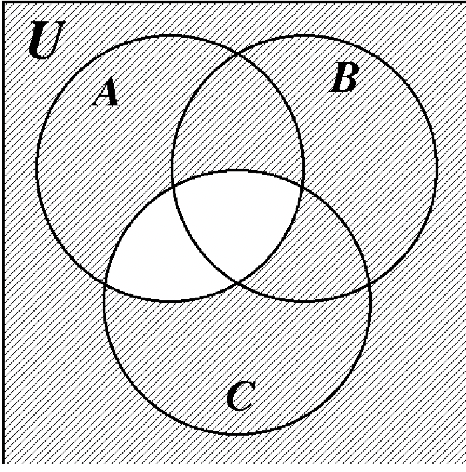 50.
50. 51. Nada está sombreado.
51. Nada está sombreado.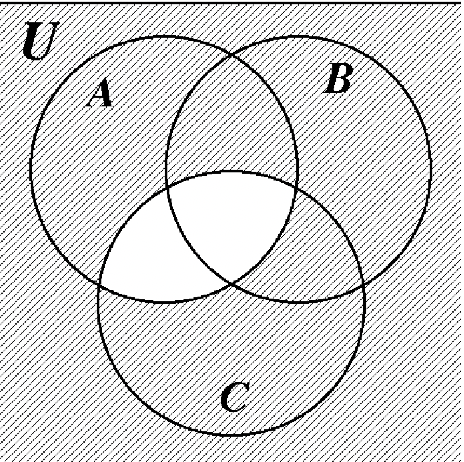 52.
52. 53.
53.En la sección Tarjeta de material hay plantillas de diagrama Venn en blanco que puedes usar para practicar.


