1.3: Más sobre Sets
- Page ID
- 113204
Necesitarás: Tijeras, Bloques A (Tarjetas de Material 2A-2E), un Póster grande con un diagrama Venn de tres juegos dibujado en él. Si no tienes póster, mira el diagrama a la izquierda. Los guiones indican dónde puedes pegar cuatro hojas de papel o cartulina (o dos carpetas de archivo abiertas) juntas y luego dibujar un diagrama grande de Venn de tres conjuntos.
Ahora que has dominado el sombreado de diagramas de Venn (no te rías), es el momento de sacar tu Conjunto de bloques A (que incluyen las tarjetas de etiqueta de valor blancas). Cada círculo representa un conjunto y estaremos etiquetando cada círculo con diferentes tarjetas de etiquetas de valor (las tarjetas blancas en cada conjunto de bloques A) en los distintos ejercicios.
Comience por elegir un valor (un color, forma o tamaño en particular). Ponga su tarjeta de etiqueta de valor - R ed, B lue, G reen, Y ellow, T riangle, s Q uare, C ircle, S mall o L arge en uno de los círculos (representando un conjunto) en el diagrama de Venn. Coloque todos los bloques A que tengan ese valor (por ejemplo, todos los cuadrados) en ese círculo. Deja ahí esas piezas. Ahora elige otro valor y pon su tarjeta de etiqueta en uno de los otros círculos. Coloca todos los bloques A que tengan este segundo valor en este segundo círculo. Observe que los círculos se superponen. Asegúrese de que una pieza de un valor no esté en la superposición a menos que también pertenezca al otro círculo. Puedes usar abreviaturas al responder estas preguntas.
¿Cuál fue tu primer valor? ____ ¿Cuál fue tu segundo valor? ____
¿Alguna pieza pertenecía a ambos círculos? ____ Si es así, ¿cuáles? ____
¿Cómo llamamos el solapamiento? ____
Ahora agrega un tercer valor para el tercer círculo en el Venn.
¿Cuál fue tu tercer valor? ____
Coloca las 24 piezas en el póster para que cada una esté en la región correcta. Tenga en cuenta que hay ocho regiones diferentes en el diagrama de Venn. Algunas piezas podrían estar fuera de los tres círculos. Todo depende de los valores que escojas. Para comprobarte, mira cuidadosamente cada círculo (que representa un Set), uno a la vez. Digamos que los cuadrados era el valor que elegiste para un círculo. Hay cuatro regiones en ese círculo. Todas las plazas deben estar en uno de esos cuatro puntos. Ahora revisa cada uno de los dos círculos siguientes, uno a la vez. Si un círculo tuviera un valor de pequeño, cada pieza pequeña debe estar en una de las cuatro regiones de ese círculo. Por último, comprobarás el tercer círculo. La mayoría de la gente tiene problemas para hacerlo exactamente bien la primera vez. Simplemente trabaje hasta que esté satisfecho cada elemento está en su lugar apropiado. Asegúrate de que todas las 24 piezas estén contabilizadas y que revises tu trabajo mirando cada juego individualmente. Después, en el diagrama de Venn en blanco que se muestra en la parte superior de la página siguiente, use abreviaturas para designar dónde se colocó cada pieza. Además, etiquete cada círculo con el valor que elegiste para ese conjunto. ¿Cuántas regiones diferentes hay en un diagrama de Venn de tres conjuntos? ____ (Pista: mira al principio de este párrafo para la respuesta.)
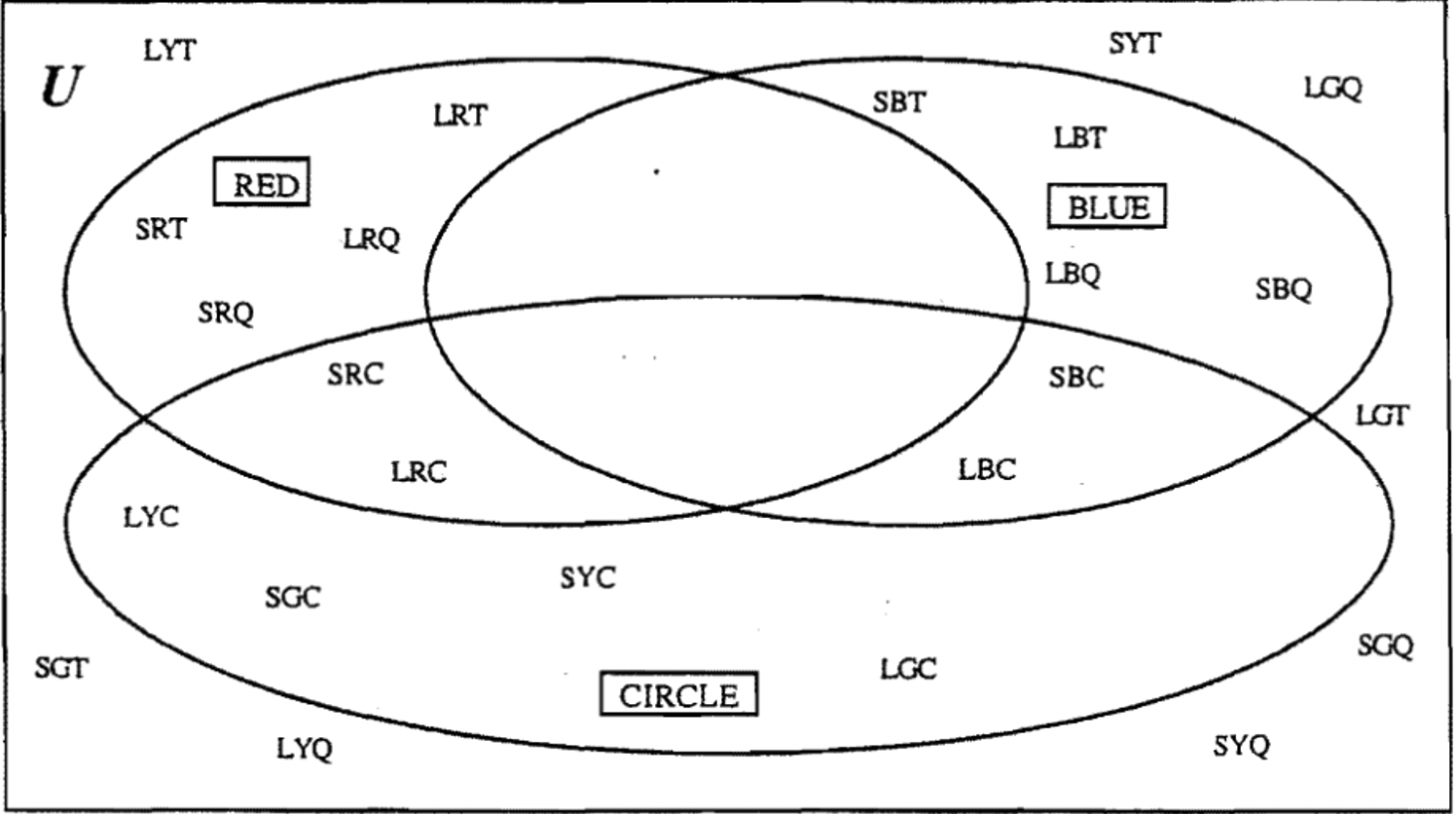
Si tuviste problemas con este primer ejercicio, quizás quieras estudiar el diagrama de Venn a continuación. Las etiquetas de valor elegidas fueron ROJO (R), AZUL (B) y CIRCLE (C). Los bloques A se muestran en su región correcta. Observe que hay dos de las ocho regiones que están vacías. Eso es porque ningún elemento es a la vez rojo y también azul! Se muestran las abreviaturas de los bloques A. Para verificar, concéntrese en un conjunto (círculo) a la vez. Todas las piezas rojas y ninguna otra deben estar en el conjunto etiquetado ROJO. Todas las piezas azules y ninguna otra deben estar en el conjunto etiquetado AZUL y todos los círculos y ninguna otra debe estar en el conjunto etiquetado CÍRCULO. Las ocho piezas restantes están fuera de los tres conjuntos. Todas las 24 piezas deben ser contabilizadas.
Hay un punto que quiero hacer sobre el dibujo de diagramas de Venn. Los conjuntos que dibujas en un diagrama de Venn dado no tienen que ser círculos y tampoco tienen que ser del mismo tamaño. Sólo hay que encerrar algún espacio. En el problema anterior, te habrás dado cuenta de que estiré los sets. Lo hice así sería menos concurrido para llenar la colocación de A cuadras. A continuación se presentan tres diagramas de Venn que contienen tres conjuntos cada uno. A pesar de que son poco convencionales, son legítimos y funcionan bien. Simplemente suele ser conveniente hacer una plantilla y pegarse con ella para uniformidad.
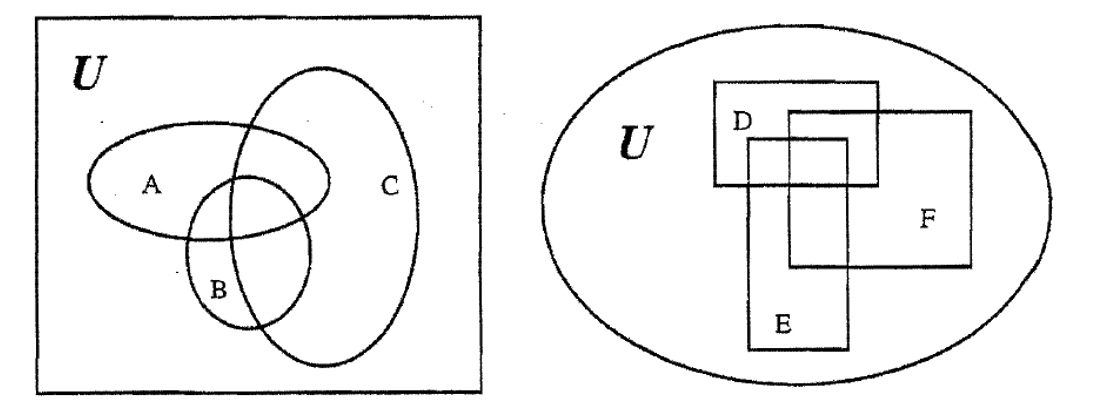
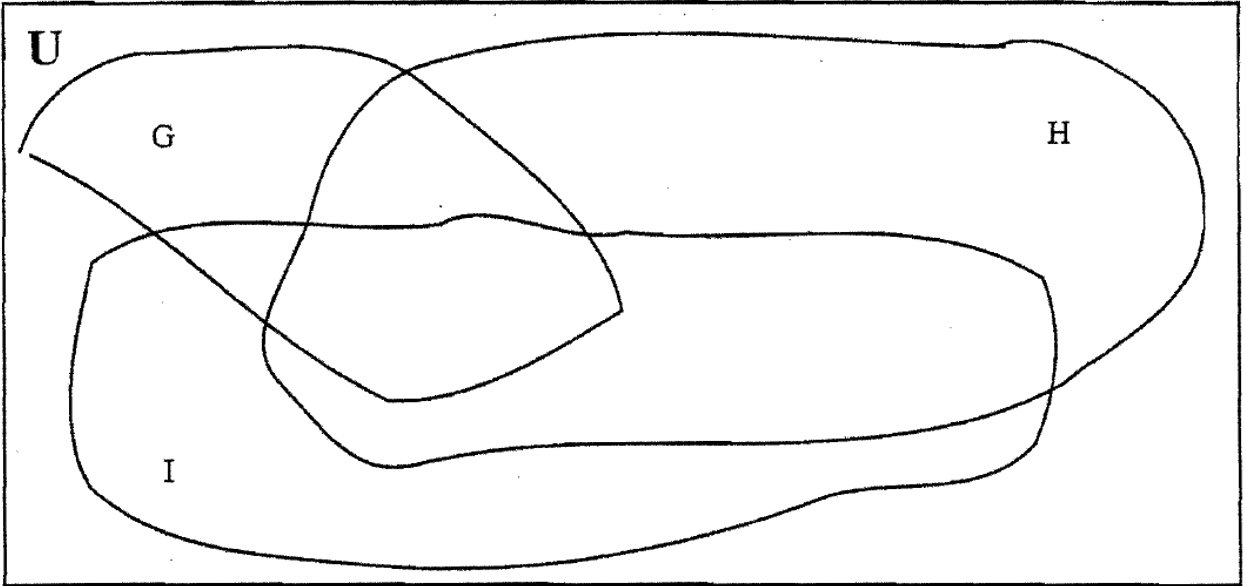
En los siguientes ejercicios, he estirado los sets para ti así que será menos concurrido rellenar las abreviaturas para la colocación de A—blocks.
Repita el ejercicio #1 en cada uno de los siguientes diagramas de Venn pero use las tres tarjetas de etiquetas de valor que se muestran para sus tres conjuntos. Primero, usa tus bloques A para colocar cada elemento en la región correcta en el póster. Asegúrese de colocar las 24 piezas en algún lugar dentro del diagrama de Venn (hay ocho regiones diferentes, y cada pieza pertenece exactamente a una de esas ocho regiones). Revisa tu trabajo mirando cada set de forma individual. Después de que se sienta seguro de que tiene todas las piezas colocadas en la región correcta, verifique su solución con la solución que se muestra en el módulo de solución. Después, en cada diagrama de Venn que se muestra en la página, escriba dónde colocó las piezas — use abreviaturas de tres letras o una representación de imagen. Debes estar seguro de que dado cualquier bloque A en particular, podrías colocarlo en la región correcta.
a. Valores: PEQUEÑO (S), VERDE (G), CIRCULO (C)
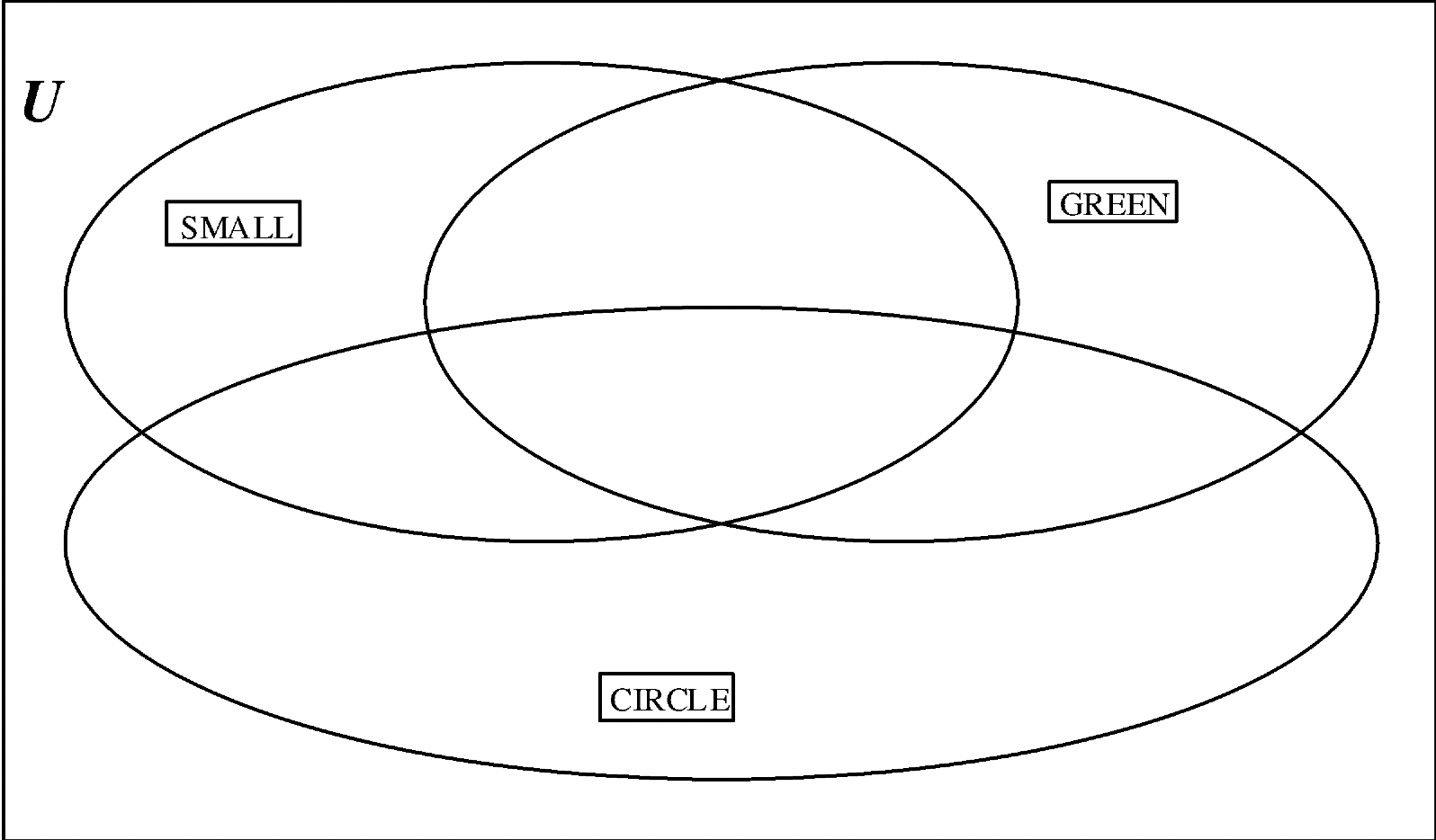
b. valores: ROJO (R), AMARILLO (Y), TRIANGULO (T)
c. Valores: CUADRADO (Q), CIRCULO (C), TRIANGULO (T)

d. valores: AZUL (B), ROJO (R), VERDE (G)

e. Informar un nuevo problema propio ahora, etiquetando cada conjunto con un valor de sus tarjetas de etiqueta de valor como en los ejercicios anteriores. Mostrar la solución de donde se colocó cada bloque en el diagrama de Venn a continuación.
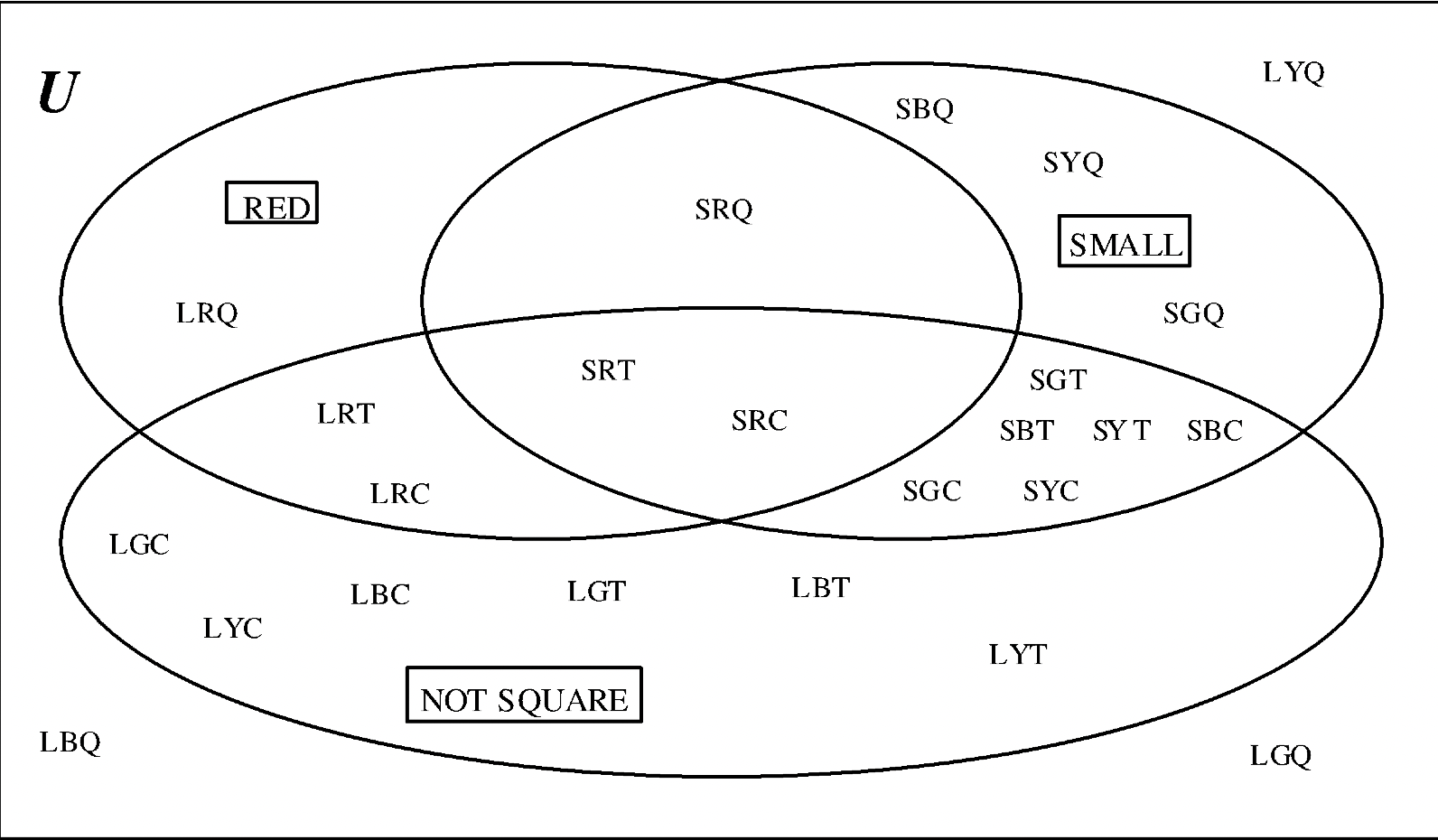
A continuación se muestra una imagen de un diagrama de Venn donde se eligen las etiquetas NOT SQUARE (\( \bf Q^{c}\)), RED (R) y SMALL (S). Es fácil de verificar porque me aseguro que solo las piezas rojas y todas las piezas rojas están en el círculo ROJO, todas las piezas pequeñas y no grandes están en el círculo PEQUEÑO y solo las casillas están fuera del círculo NO CUADRADO. Se contabilizan las 24 piezas.
Usa algunos valores negativos (NO) ahora. PEQUEÑO y GRANDE pueden considerarse como valores positivos o negativos porque PEQUEÑO es lo mismo que NO GRANDE. Etiquete cada juego con un valor negativo de sus tarjetas de etiquetas de valor. Después de colocar las piezas en el cartel y verificar, mostrar la solución de dónde se colocaron al menos ocho bloques A en el diagrama de Venn a continuación.

Algunas tarjetas de etiquetas de valor negativo se muestran en los siguientes diagramas de Venn. Usa tus bloques A para colocar cada bloque A en la región correcta en el póster. Asegúrate de dar cuenta de las 24 piezas y revisa tu trabajo mirando cada juego individualmente. Después, en cada diagrama de Venn mostrado, use abreviaturas para designar dónde se colocaron ocho piezas.
a. Valores: NO AZUL (\(\bf B^{c}\)), GRANDE (L), NO AMARILLO (\(\bf Y^{c}\))
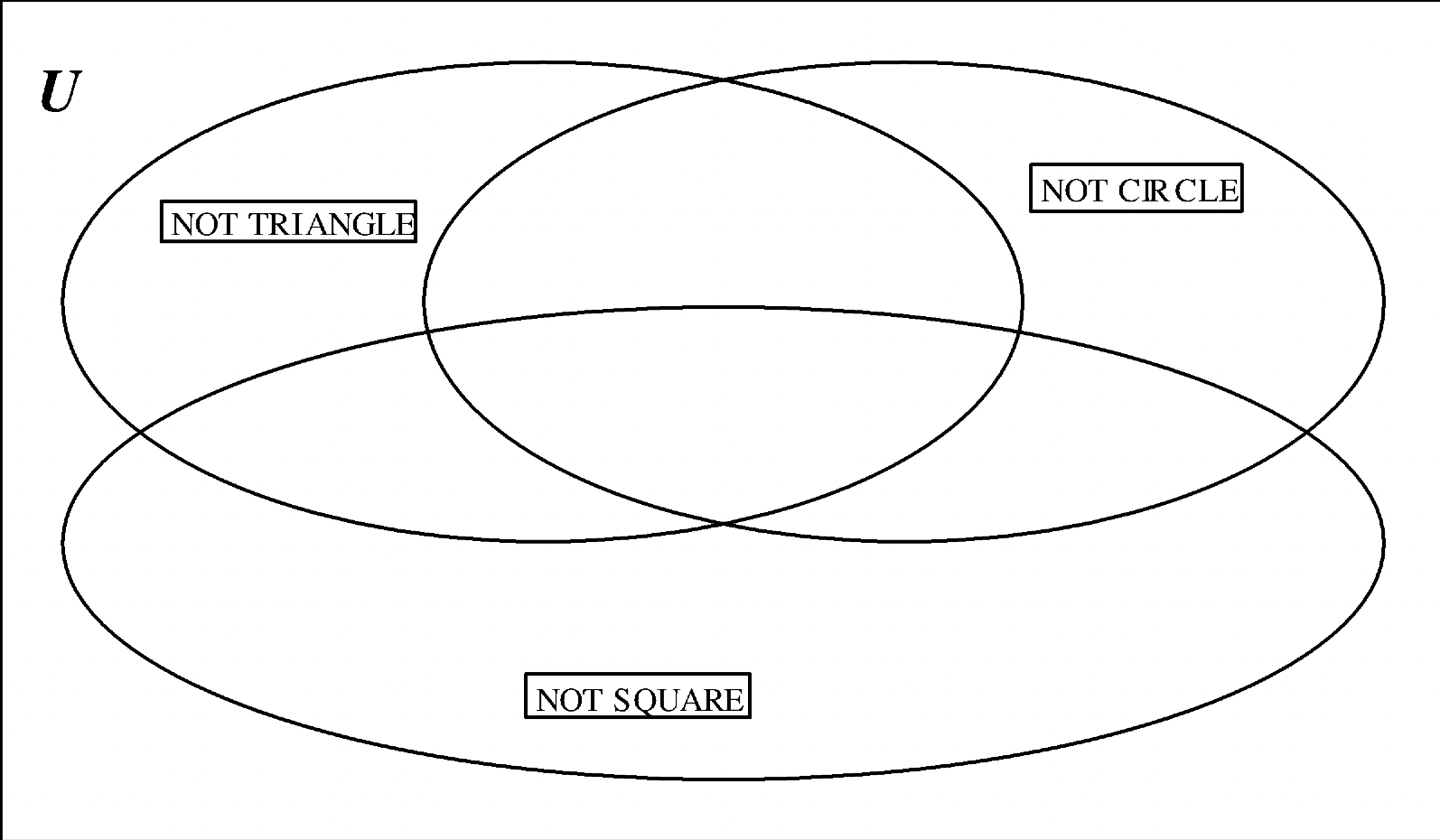
b. Valores: NO TRIÁNGULO (\(\bf \bar{T}\)), NO CIRCULO (\(\bf \bar{C}\)), NO CUADRADO (\(\bf \bar{Q}\))
c. Valores: AZUL (B), CUADRADO (Q), NO ROJO (\(\bf R^{c}\))
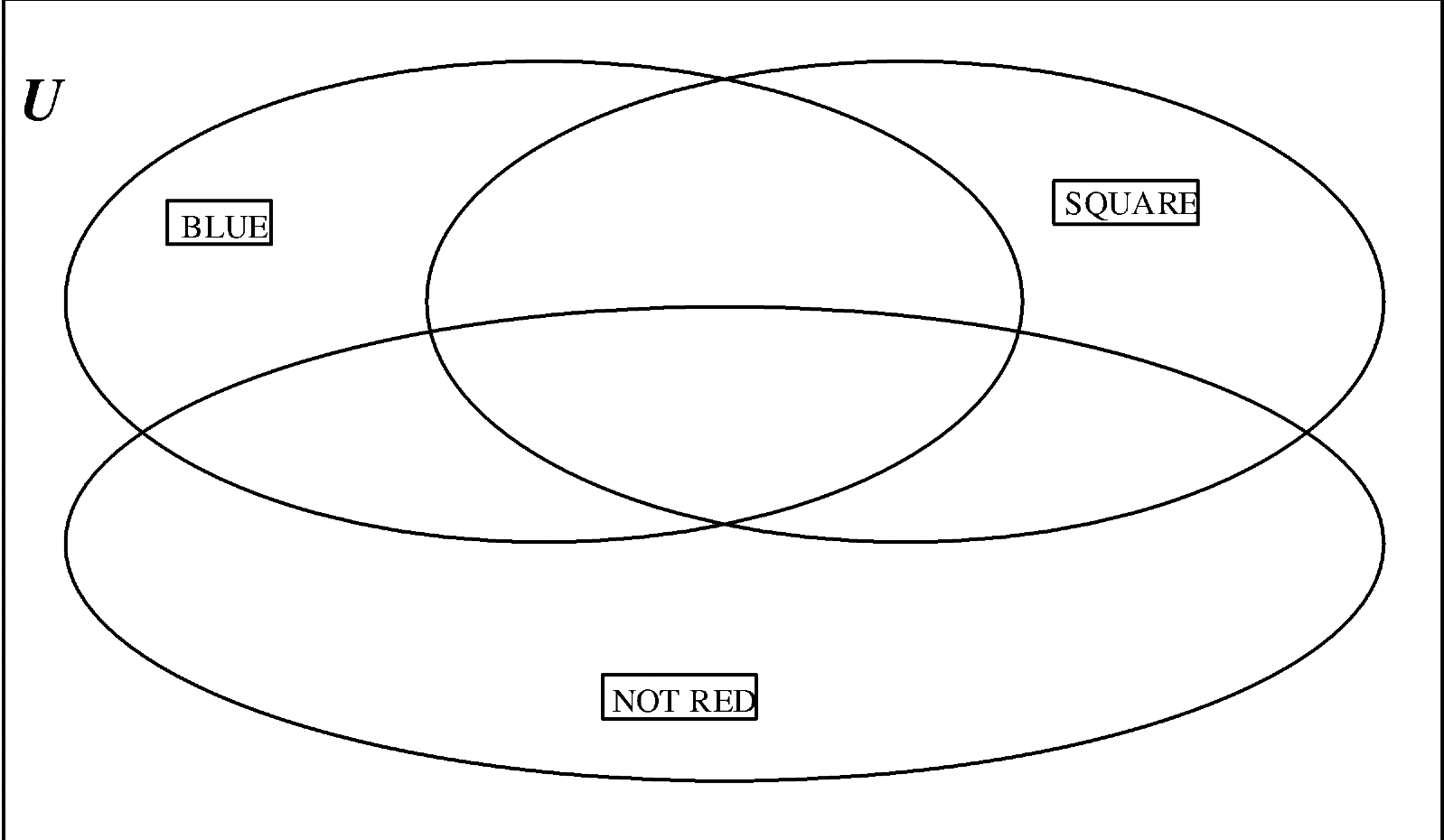
Nombra algunas combinaciones de etiquetas de valor que no dejen piezas fuera de los tres conjuntos.
Nombra algunas combinaciones que dejen exactamente una pieza fuera de los tres conjuntos. [Pista 1: Elige una pieza que quieras que te quede fuera. Pista 2: Usa algunas etiquetas NOT.]
Anota algunas combinaciones que dejen la mayor cantidad de piezas fuera de los sets. ¿Cuál crees que es la mayor cantidad de piezas que se pueden dejar fuera de los tres círculos?
Toma una de tus tarjetas de etiqueta de valor en blanco y en ella, escribe\(\bf B \cup Q\) (para la UNIÓN de AZUL y CUADRADO). Toma las tarjetas de etiquetas NOT BLUE (\(\bf B^{c}\)) y NOT SQUARE (\(\bf Q^{c}\)) de tu set. En el cartel, pon cada etiqueta en uno de los sets. Coloque cada bloque A en la región correcta.
a. en el diagrama de Venn a continuación, muestre dónde colocó cada bloque A —.
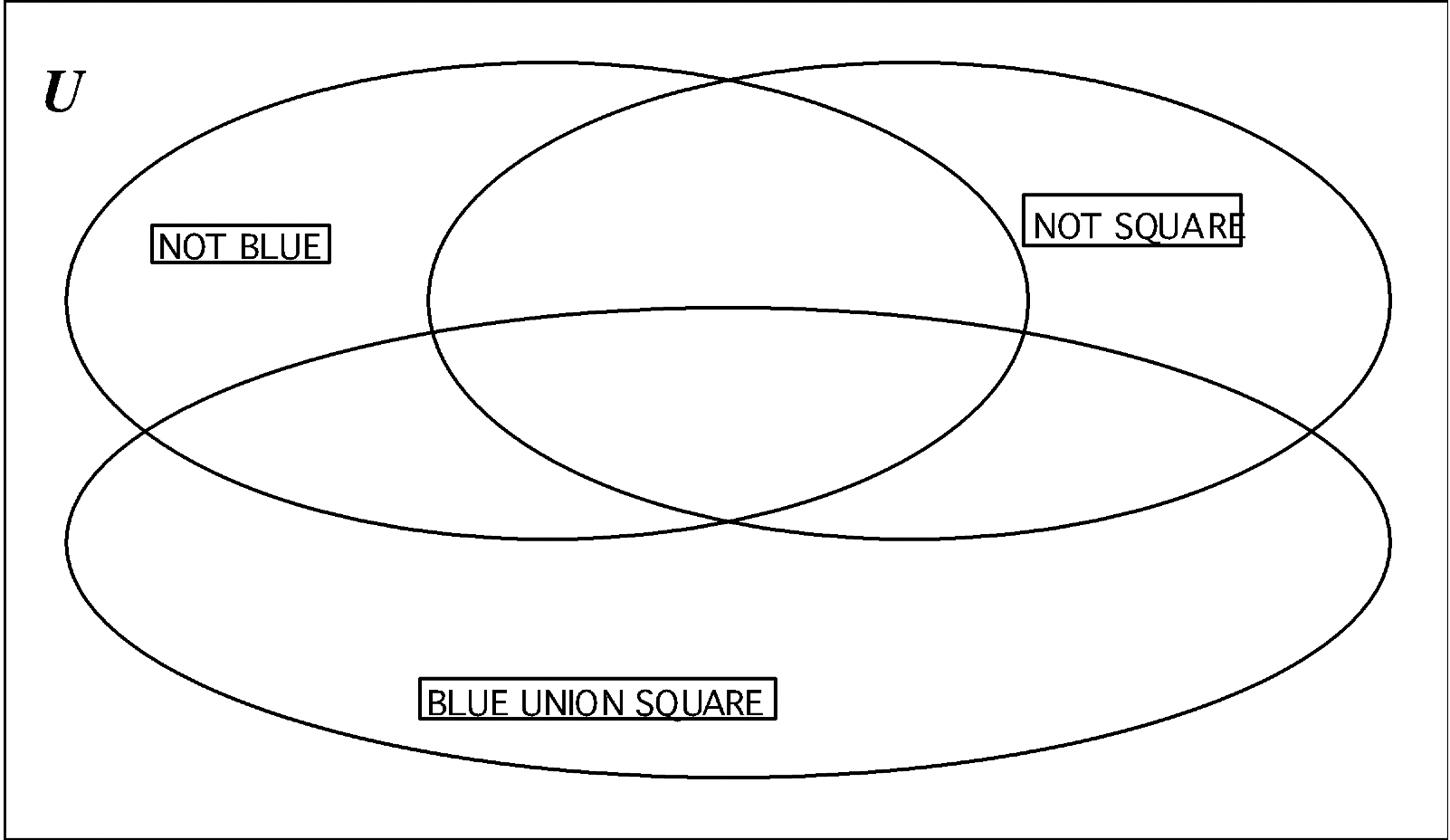
b. mira el conjunto BLUE UNION SQUARE (B\(\cup\) Q). Mira todas las piezas fuera del conjunto B\(\cup\) Q para que puedas enumerar los elementos en\(\bf (B \cup Q)^{c}\): ____
c. Mire la intersección de NOT BLUE y NOT SQUARE\(\bf B \cap Q^{c}\), y enumere sus elementos: ____
d. ¿Qué nota de los elementos enumerados en la parte b y c anteriores? ____
e. Escribe una ecuación a partir de lo que notaste. ____
Haz una tarjeta de etiqueta NOT RED UNION CIRCLE (\(\bf R^{c} \cup C\)) y toma las etiquetas RED (R) y NOT CIRCLE (\(\bf C^{c}\)) de tu set.
a. Siguiendo las instrucciones del ejercicio 8 con estas tres nuevas etiquetas, muestra dónde colocó cada bloque A en el diagrama de Venn a continuación.
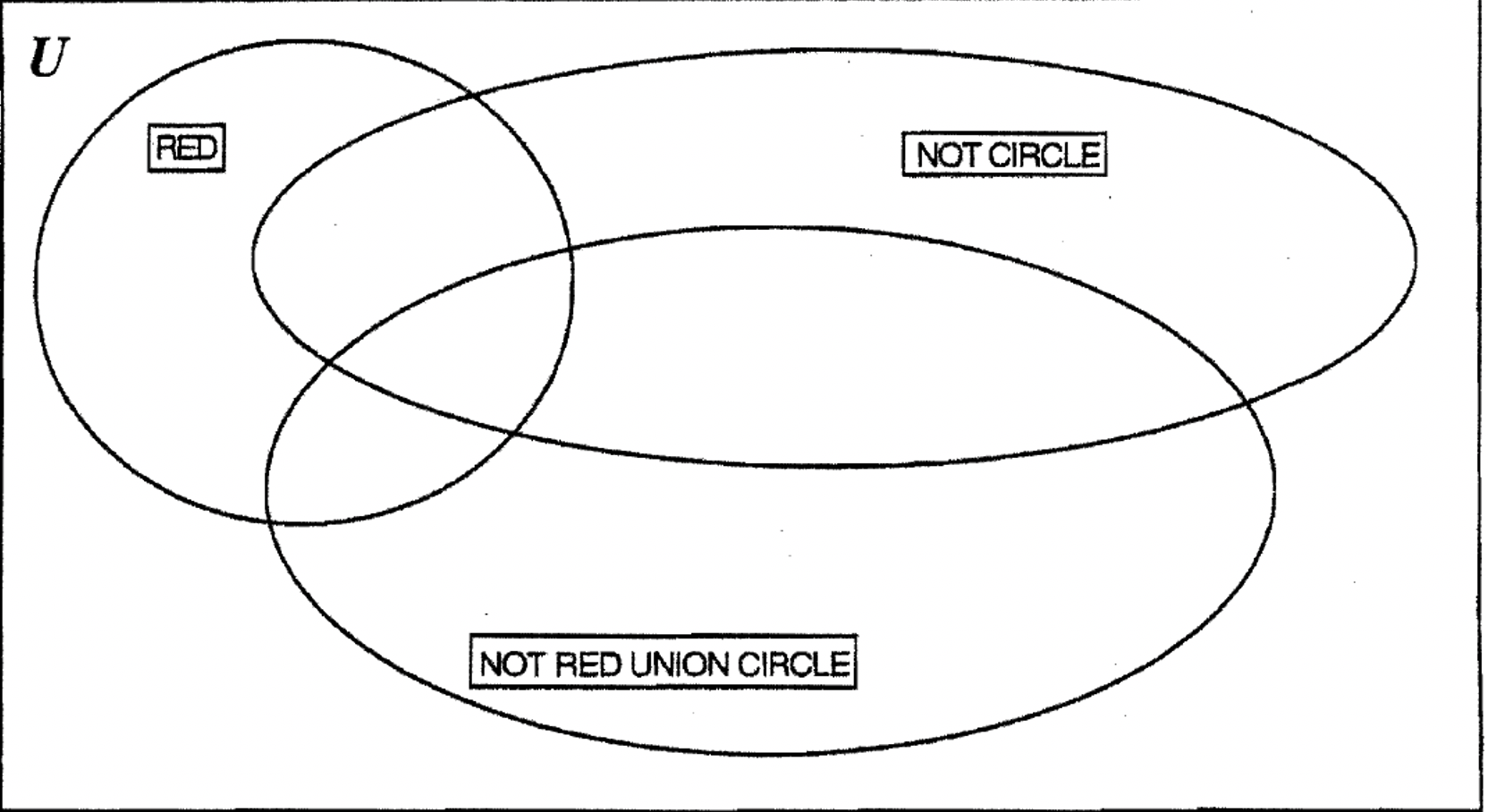
b. mira el conjunto NOT RED UNION CIRCLE (\(\bf R^{c} \cup C\)). Mira todas las piezas fuera del set\(\bf R^{c} \cup C\) para que puedas enumerar los elementos en\(\bf (R^{c} \cup C)^{c}\): ____
c. Mire la intersección de RED y NOT CIRCLE (\(\bf R \cap C^{c}\)) y enumere sus elementos: ____
d. ¿Qué nota de los elementos enumerados en la parte b y c anteriores? ____
e. Escribe una ecuación a partir de lo que notaste. ____
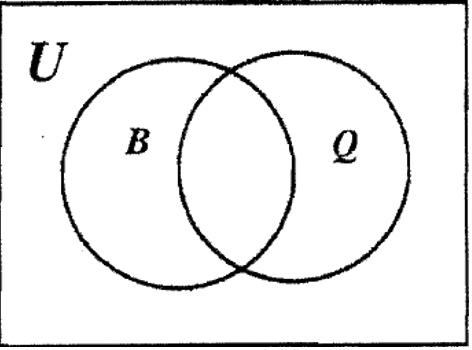
a. abajo, en el diagrama de Venn a la izquierda, sombra con líneas verticales y sombra\(\bf B^{c}\) con líneas horizontales. Observe la superposición de ambas líneas y sombree esta\(\bf Q^{c}\) intersección en el diagrama de Venn a la derecha. Por lo tanto, el Venn de la derecha representa\(\bf (B^{c} \cap Q^{c})\).
 |
 |
b. abajo, en el diagrama de Venn a la izquierda, sombra\(\bf B \cup Q\). En el diagrama de Venn a la derecha, sombrea todo excepto\(\bf B \cup Q\). Entonces, el Venn de la derecha representa\(\bf (B \cup Q)^{c}\).
 |
 |
c. ¿Qué nota sobre los sombreados para\(\bf (B^{c} \cap Q^{c})\) y\(\bf (B \cup Q)^{c}\) (los Venns a la derecha para a y b)?
d. Escribe una ecuación a partir de lo que notaste ___
Abajo, en el diagrama de Venn a la izquierda, sombra\(\bf (A \cap B)^{c}\). En el diagrama de Venn a la derecha, sombrea\(\bf A^{c}\) con líneas verticales y\(\bf B^c\) con líneas horizontales. En conjunto, el sombreado total de la derecha representa\(\bf A^{c} \cup B^{c}\).
|
a.\(\bf (A \cap B)^{c}\)  |
b.\(\bf A^{c} \cup B^{c}\)  |
c. ¿Para qué notas sobre los sombreados\(\bf (A \cap B)^{c}\) y\(\bf A^{c} \cup B^{c}\)?
d. Escribe una ecuación a partir de lo que notaste ____
Los ejercicios 8, 9, 10 y 11 ilustran ejemplos de las leyes de DeMorgan.
Una ley establece que\(\bf (A \cup B)^{c} = A^{c} \cap B^{c}\).
Eso lo establece la otra Ley de DeMorgan\(\bf (A \cap B)^{c} = A^{c} \cup B^{c}\).
Recuerda que A y B son solo variables ficticias.
Básicamente, en inglés, la primera de las Leyes de DeMorgan (\(\bf (A \cup B)^{c} = A^{c} \cap B^{c}\)) dice que el complemento de la unión de dos conjuntos es igual a la intersección del complemento de cada conjunto. A continuación se dan algunos ejemplos de esta ley.
| \(\bf (M \cup N)^{c} = M^{c} \cap N^{c}\) | \(\bf (L^{c} \cup K)^{c} = L \cap K^{c}\) | \(\bf (X^{c} \cup Y^{c})^{c} = X \cap Y\) |
Me gusta pensar en ello como distribuir el complemento sobre los paréntesis. Para eliminar los paréntesis, tomar el complemento de cada uno de los dos conjuntos entre paréntesis y cambiar la unión a intersección.
El segundo de las Leyes de DeMorgan (\(\bf (A \cap B)^{c} = A^{c} \cup B^{c}\)) dice que el complemento de la intersección de dos conjuntos es igual a la unión del complemento de cada conjunto. Nuevamente, es como distribuir el complemento sobre los paréntesis. Pero esta vez, la intersección cambia a unión cuando se eliminan los paréntesis. Aquí hay algunos ejemplos de esta ley:
| \(\bf (M \cap N)^{c} = M^{c} \cup N^{c}\) | \(\bf (L^{c} \cap K)^{c} = L \cup K^{c}\) | \(\bf (X^{c} \cap Y^{c})^{c} = X \cup Y\) |
Si se le da la unión o intersección de cualquiera de dos conjuntos, puede utilizar la Ley de DeMorgan para escribirla como complemento de una cantidad. Por ejemplo, si alguien te pidió que escribieras una declaración equivalente para\(\bf R \cup S^{c}\), usas las Leyes de DeMorgan para escribirla como\(\bf (R^{c} \cap S)^{c}\). Observe cómo se hace esto: Para obtener paréntesis con un complemento fuera de él cuando no hay ninguno para empezar, como en\(\bf R \cup S^{c}\), comenzar por poner paréntesis con un complemento y espacio para poner algo dentro así:\(\bf R \cup S^{c}\) =\(( \ )^{c}\). Para averiguar qué pasa dentro, cambia las tres partes originales por sus “opuestos”. De R a\(R^{c}\), de\(\cup\) a\(\cap\), y de\(S^{c}\) a S. Esto da uso\(\bf R \cup S^{c}\) =\(\bf (R^{c} \cap S)^{c}\). Tendrás que usar esta técnica para 12b, d y f.
Use las leyes de DeMorgan para escribir una expresión equivalente para cada declaración a continuación.
| \(\bf (R^{c} \cap S^c)^{c}\) | \(\bf M \cap N\) |
| \(\bf (F \cup G^{c})^{c}\) | \(\bf H^{c} \cup I\) |
| \(\bf (P^{c} \cap Q)^{c}\) | \(\bf S \cap T^{c}\) |
Informar dos de sus propias declaraciones equivalentes (como en el ejercicio 12) para demostrar la Ley de DeMorgan.
| a. | b. |
Es hora de demostrar las leyes de DeMorgan de otra manera. De vuelta en Ejercicio Set 1, ejercicio 13, trabajaste en problemas donde dejamos que U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, y definimos estos subconjuntos de U: A = {1, 2, 3, 4, 5} B = {2, 4, 6, 8} C = {3, 5, 7}. Usaremos estos conjuntos definidos para calcular lo siguiente y, por lo tanto, verificar las leyes de DeMorgan:
Ejemplo
Mostrar que =\(\bf (A \cap B)^{c} = A^{c} \cup B^{c}\).
Solución
Para mostrar que los dos lados son iguales, primero simplifique el lado izquierdo calculando la intersección de A y B, (enumerando los elementos de cada uno y luego enumerando los elementos en la intersección). Entonces toma el complemento de ese conjunto.
\(\bf (A \cap B)^{c} = (\{1, 2, 3, 4, 5\} \cap \{2, 4, 6, 8\})^{c} = (\{2,4\})^c = \{1, 3, 5, 6, 7, 8, 9\}\)
Segundo, simplificar el lado derecho calculando el complemento de A y también el complemento de B, para luego tomar la unión de esos dos conjuntos.
\(\bf A^c \cup B^{c} = (\{1, 2, 3, 4, 5\})^{c} \cup (\{2, 4, 6, 8\})^{c} = \{6, 7, 8, 9\} \cup \{1, 3, 5, 7, 9\} = \{1, 3, 5, 6, 7, 8, 9\}\)
Ya que\(\bf (A \cap B)^{c}\) y\(\bf A^c \cup B^{c}\) tienen exactamente los mismos elementos, son iguales.
Por lo tanto,\(\bf (A \cap B)^{c} = A^{c} \cup B^{c}\)
Sea U = {1, 2, 3, 4, 5, 6, 7, 8, 9} y estos subconjuntos definidos:
| A = {1, 2, 3, 4, 5} | B = {2, 4, 6, 8} | C = {3, 5, 7} |
Verifica lo siguiente. Mostrar todos los pasos como se ha hecho en el ejemplo anterior. Declarar la conclusión final en palabras.
a. Demostrar que\(\bf (A \cup B)^{c} = A^{c} \cap B^{c}\)
b. Demostrar que\(\bf (A \cap C)^{c} = A^{c} \cup C^{c}\)
c. Demostrar que\(\bf (B^{c} \cup C)^{c} = B \cap C^{c}\)
Usted ha visto las leyes de DeMorgan demostradas de muchas maneras. ¿Crees que los recordarás? Hubo varios ejercicios que hiciste en el Ejercicio Set 2 demostrando estas leyes. Ahora es un buen momento para mirar hacia atrás a estos pares de ejercicios de diagrama de Venn que sombreaste en el Set de ejercicios 2 #'s 25 y 28, 26 y 29, 44 y 45 y 50 y 52.
Es momento de demostrar dos propiedades más interesantes sobre conjuntos.
a. sombrearemos diagramas de Venn representando\(\bf A \cap (B \cup C)\) y\(\bf (A \cap B) \cup (A \cap C)\). A la izquierda diagrama de Venn, sombra A con líneas horizontales\(\bf B \cup C\) y con líneas verticales. Entonces, el solapamiento es\(\bf A \cap (B \cup C)\). Sombra solo la superposición en el diagrama de Venn medio. Ya que\(\bf (A \cap B) \cup (A \cap C)\) es una unión, sombra\(\bf A \cap B\) tanto como\(\bf A \cap C\) en el diagrama de Venn derecho.
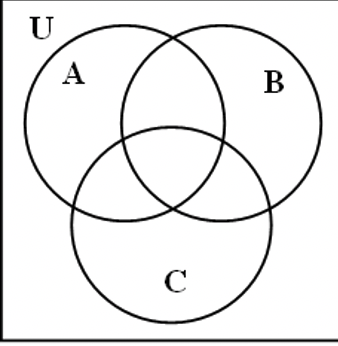 |
 \(\bf A \cap (B \cup C)\) \(\bf A \cap (B \cup C)\) |
 \(\bf (A \cap B) \cup (A \cap C)\) \(\bf (A \cap B) \cup (A \cap C)\) |
b. ¿Qué notas sobre los sombreados finales de los diagramas de Venn para\(\bf A \cap (B \cup C)\) y\(\bf (A \cap B) \cup (A \cap C)\)?
Al igual que en el ejercicio 14, vamos a U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, y defina estos subconjuntos de U:
| A = {1, 2, 3, 4, 5} | B = {2, 4, 6, 8} | C = {3, 5, 7} |
Compute lo siguiente:
c.\(\bf A \cap (B \cup C)\) = ____
d.\(\bf (A \cap B) \cup (A \cap C)\) = ____
e. ¿Qué notas sobre las respuestas para c y d? ____
a. sombrearemos diagramas de Venn representando\(\bf (A \cup B) \cap (A \cup C)\) y\(\bf A \cup (B \cap C)\). A la izquierda diagrama de Venn, sombra\(\bf A \cup B\) con líneas horizontales y\(\bf A \cup C\) con líneas verticales. Entonces, el solapamiento es\(\bf (A \cup B) \cap (A \cup C)\). Sombra solo la superposición en el diagrama de Venn medio. Ya que\(\bf A \cup (B \cap C)\) es una unión, sombra tanto A como\(\bf B \cap C\) a la derecha diagrama de Venn.
 |
 \(\bf (A \cup B) \cap (A \cup C)\) \(\bf (A \cup B) \cap (A \cup C)\) |
 \(\bf A \cup (B \cap C)\) \(\bf A \cup (B \cap C)\) |
b. ¿Qué notas sobre los sombreados finales de los diagramas de Venn para\(\bf (A \cup B) \cap (A \cup C)\) y\(\bf A \cup (B \cap C)\)?
Al igual que en el ejercicio 14, vamos a U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, y defina estos subconjuntos de U:
| A = {1, 2, 3, 4, 5} | B = {2, 4, 6, 8} | C = {3, 5, 7} |
Compute lo siguiente:
c.\(\bf A \cup (B \cap C)\) = ____
d.\(\bf (A \cup B) \cap (A \cup C)\) = ____
e. ¿Qué notas sobre las respuestas para c y d? ____
Los ejercicios 15 y 16 demuestran dos propiedades distributivas de conjuntos.
El primero distribuye intersección sobre unión:
Para tres juegos, A, B y C, \(\bf A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\).
El segundo distribuye unión sobre intersección:
Para tres juegos, A, B y C, \(\bf A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\).
A continuación se presentan algunos ejemplos de estas propiedades.
\(\bf A^{c} \cup (M^{c} \cap N) = (A^{c} \cup M^{c}) \cap (A^{c} \cup N)\)
\(\bf (B \cap T^{c}) \cup (B \cap S) = B \cap (T^{c} \cup S)\)
Utilice las propiedades distributivas de conjuntos para reescribir cada uno de los siguientes (no se desprenda por complementos):
a.\(\bf X \cap (Y \cup Z)\) = ____
b.\(\bf P \cup (Q^{c} \cap R)\) = _____
c.\(\bf (K^{c} \cap L) \cup (K^{c} \cap M)\) = ______
d.\(\bf (D \cup E^{c}) \cap (D \cup F)\) = _____
Los ejercicios 53 y 54 en el Ejercicio Set 2 demostraron una de las leyes distributivas. Ahora es un buen momento para mirar hacia atrás a estos.


