2.4: Otros Sistemas Base
- Page ID
- 113191
Necesitarás: * Base Dos Bloques, Base Tres Bloques, Base Cuatro Bloques, Bloques Unitarios (Tarjetas de Material 4 - 7), Calculadora
Los bloques reales son tridimensionales. Las unidades, largos y planos de las tarjetas de material solo se muestran en 2 dimensiones, por lo que no serían demasiado engorrosos de hacer. Tienes que imaginarte que realmente están hechos de cubos. Las unidades son como dados. En la base tres, un largo es de 3 unidades juntas, por lo que las dimensiones son realmente de 3 por 1 por 1 y un plano se compone de 3 largos, por lo que las dimensiones son realmente de 3 por 3 por 1.
Puedes consultar los bloques base de tu instructor. Simplemente envíale un correo electrónico solicitando que se los preste.
A continuación se muestra un dibujo amateur de cómo se ve realmente una unidad, larga, plana y bloque en Base Tres.
|
Base Tres unidades 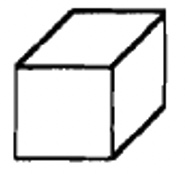 |
Base Tres unidades 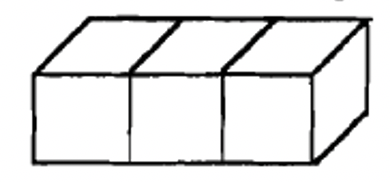 |
|
Base Tres unidades 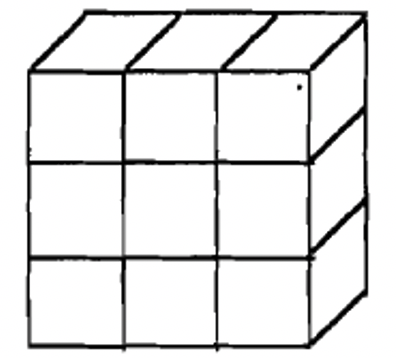 |
Base Tres unidades 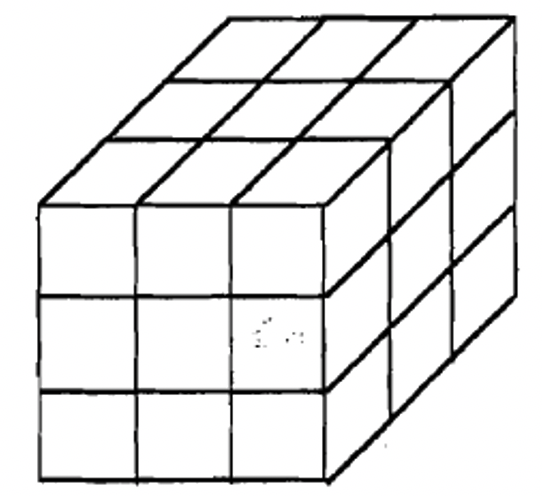 |
Ya que solo vivimos en un mundo tridimensional, una vez que superamos un bloque, realmente no podemos dibujar en la 4ta dimensión o superior. Bueno, al menos no puedo. En Base Tres, se necesitan tres unidades para hacer un largo, se necesitan tres largos para hacer un piso y se necesitan tres pisos para hacer un bloque. En Base Tres, el siguiente nivel después de un bloque se hace poniendo tres bloques juntos y a eso lo llamamos bloque largo. Tres bloques largos juntos se llama bloque plano, y tres bloques planos juntos se llama bloque de bloque.
En Base Tres, una unidad está compuesta por 1 cubo, una larga está compuesta por 3 cubos, una plana está compuesta por 9 cubos, un bloque está conformado por 27 cubos, un bloque largo está conformado por 81 cubos, un bloque plano está compuesto por 243 cubos, y un bloque de bloque está compuesto por 729 cubos.
Base Dos bloques son diferentes. En Base Dos, se necesitan dos unidades para hacer un largo, se necesitan dos largos para hacer un piso y se necesitan dos pisos para hacer un bloque. En Base Dos, el siguiente nivel después de un bloque se hace juntando dos bloques y a eso lo llamamos bloque largo. Dos bloques largos juntos se llama bloque plano, y dos bloques planos juntos se llama bloque de bloque. Intenta imaginar cómo se ve una unidad, larga, plana y bloque en Base Dos antes de pasar la página.
A continuación se muestra un dibujo amateur de una unidad, larga, plana y bloque en Base Dos.
|
Base Dos unidades 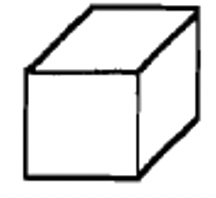 |
Base Dos largos 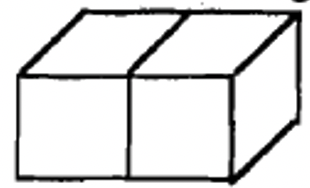 |
Base Dos plana 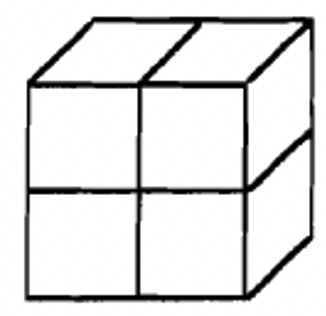 |
Base de dos bloques 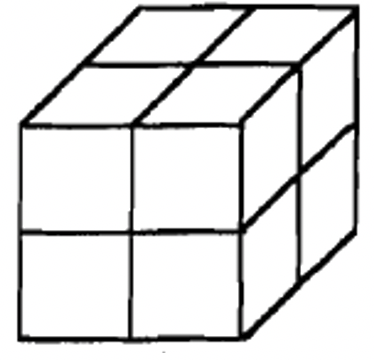 |
En la base dos, una unidad está compuesta por 1 cubo, una larga está compuesta por 2 cubos, una plana está compuesta por 4 cubos, un bloque está conformado por 8 cubos, un bloque largo está compuesto por 16 cubos, un bloque plano está compuesto por 32 cubos, y un bloque de bloque está compuesto por 64 cubos.
Dibuja una imagen de una unidad Base Cuatro, larga, plana y en bloque.
Rellene los espacios en blanco.
a. en Base Cuatro, se necesitan ____ unidades para hacer un largo, se necesitan ____ largos para hacer un piso, se necesitan ____ pisos para hacer un bloque, se necesitan ____ bloques para hacer un bloque largo, toma ____ bloques largos para hacer un bloque plano, y toma ____ bloques planos para hacer un bloque de bloque.
b. en Base Cuatro, una unidad está compuesta por 1 cubo, una larga está compuesta por ______ cubos, un plano está compuesto por ______ cubos, un bloque está formado por ______ cubos, y un bloque largo está compuesto por ______ cubos.
c. En la Base Cinco, se necesitan ______ pisos para hacer un bloque.
d. En la Base Seis, un piso se compone de ______ cubos.
Ahora que tiene experiencia en convertir de otras bases a Base Diez, nos enfocaremos en convertir de Base Diez a otras bases. Hay más de una manera de lograr esta tarea. Aprenderás a hacerlo usando dos enfoques diferentes y luego podrás elegir usar el método que mejor funcione para ti cuando trabajes en los ejercicios. Es óptimo si entiendes y puedes convertir usando cualquiera de los dos métodos porque como profesor, un alumno puede entender una explicación perfectamente mientras que otro estudiante podría entenderla mejor si se explicara de manera bastante diferente.
¡Salgan los bloques y resuelvan estos problemas USANDO LOS BLOQUES!
Antes de usar cualquiera de los dos métodos, quiero que regreses al proceso de intercambio como lo hiciste al inicio de este conjunto de ejercicios. En lugar de usar los Modelos Base Dos, esta vez usaremos conjuntos de Bloques Base en Base Dos, Base Tres y Base Cuatro. Puedes tener juegos tridimensionales de madera o plástico en tu salón de clases o puedes hacer tus propios modelos usando Tarjetas de Materiales 9-11. Recuerda que las tarjetas de material para las unidades, longs y flats son sólo bidimensionales. Mantenga los juegos separados entre sí. Las unidades son las mismas para cualquier conjunto de Bloques Base por lo que solo necesitas un total de un juego de unidades.
¡Estos tres ejercicios siguientes deberían ser pan comido para ti!
Saca tu juego de Base Dos Bloques. Estos consisten en al menos unidades, largos, pisos, bloques, bloques largos y bloques planos. ¿Cuántas unidades hay en un largo? _____ ¿Cuántos anhelos hay en un piso? _____ ¿Cuántos pisos hay en una cuadra? _____ ¿Cuántos bloques hay en un bloque largo? _____ ¿Cuántos bloques largos hay en un bloque plano? _____
Saca tu juego de Base Tres Bloques. Estos consisten en al menos unidades, largos, pisos y bloques. ¿Cuántas unidades hay en un largo? _____ ¿Cuántos anhelos hay en un piso? _____ ¿Cuántos pisos hay en una cuadra? _____
Saca tu juego de Base Cuatro Bloques. Estos consisten en al menos unidades, largos, pisos y bloques. ¿Cuántas unidades hay en un largo? _____ ¿Cuántos anhelos hay en un piso? _____ ¿Cuántos pisos hay en una cuadra? _____
Gráfico de valor posicional para bloques base
| FB | LB | B | F | L | U |
Arriba hay un gráfico de valor posicional para todas las bases cuando se utilizan bloques Base. U representa unidades, L representa largos, F representa planos, B representa bloques, LB representa bloques largos y FB representa bloques planos. En general, puede haber más de seis valores posicionados, pero seis son suficientes para completar los ejercicios en este conjunto. Si está utilizando las Tarjetas de Material para Bloques Base, los bloques Base Dos tienen los seis tipos de bloques, mientras que los bloques Base Tres y Cuatro solo tienen unidades, largos, planos y bloques.
Imagina que María tuvo un bebé y ya era hora de su chequeo de seis semanas. Habían pasado exactamente seis semanas desde que se convirtió en madre. Estarás representando el número de días que María ha sido madre en Base Dos, Base Tres y Base Cuatro usando los Bloques Base.
a. para representar el número de días que María ha sido madre en Base Dos, haga lo siguiente usando Bloques Base Dos:
| i. Usando las unidades, cuente cuántos días María ha sido mamá. Tienes _____ unidades. |
| ii. Comercia las unidades por tantos largos como sea posible. Ahora tiene _____ largo (s) y _____ unidad (es). |
| iii. Comercia los anhelos por tantos pisos como sea posible. Ahora tiene _____ piso (s), _____largo (s) y _____ unidad (es). |
| iv. Comercio en los pisos por tantos bloques como sea posible. Ahora tiene _____ bloque (s), _____ plano (s), _____ largo (s) y _____ unidad (es). |
| v. Comercio de los bloques por tantos bloques largos como sea posible. Ahora tiene _____ bloque (s) largo (s), _____ bloque (s), _____ plano (s), _____ largo (s) y _____ unidad (es). |
| vi. Opere en los bloques largos por tantos bloques planos como pueda. Ahora tiene _____ bloque (s) plano (s), _____ bloque (s) largo (s), _____ bloque (s), _____ plano (s), _____ largo (s) y _____ unidad (es). |
| vii. Registrar los resultados de la parte vi. en la primera fila del gráfico en la parte d a continuación. |
Para las partes b y c, haz una serie de intercambios como hiciste en la parte a, pero usa Base Tres Bloques para la parte b y Base Cuatro Bloques para la parte c. En otras palabras, comienza con la misma cantidad de unidades que tenías en la parte a.i. y comienza intercambiando tantas unidades por largos como sea posible. Entonces, intercambia tantos anhelos por pisos como sea posible, luego pisos por bloques, etc., hasta que se hayan realizado todos los intercambios posibles. No necesitas anotar cada paso individual como lo hiciste para la parte a anterior solo usa los bloques y registra los resultados finales en la parte d.
b. comience con el mismo número de unidades que tenía en la parte a.i y haga todos los intercambios posibles usando Tres Bloques Base. Cuando se hayan realizado todas las operaciones, registre los resultados en la segunda fila del gráfico (Base Tres) en la parte d a continuación.
c. Comienza con el mismo número de unidades que tenías en la parte a.i y haz todos los intercambios posibles usando Base Cuatro Bloques. Cuando se hayan realizado todas las operaciones, registre los resultados en la tercera fila del gráfico (Base Cuatro) en la parte d a continuación.
d.
| FB | LB | B | F | L | U | Base | |
|---|---|---|---|---|---|---|---|
| resultados de la parte a: | Dos | ||||||
| resultados de la parte b: | Tres | ||||||
| resultados de la parte c: | Cuatro |
El ejercicio 4 ilustra una forma de cambiar un número en Base Diez a uno en una base diferente. Para ese ejercicio, convertiste la Base Diez numeral 42 (seis semanas de siete días cada una) a Base Dos (\(101010_{\text{two}}\)), Base Tres (\(1120_{\text{three}}\)) y Base Cuatro (\(222_{\text{four}}\)). Si no obtuviste estas respuestas, deberías reelaborar el problema usando los modelos físicos, y tener cuidado al hacer intercambios precisos. Pide ayuda si aún tienes problemas.
Usa los Bloques Base para convertir el número de semanas en un año a un numeral en cada una de las bases dadas. Primero debes comenzar con las unidades y contar tantas unidades como semanas haya en un año. Entonces, comercia en unidades por tantos largos como sea posible, luego intercambia largos por tantos pisos como sea posible y así sucesivamente. Haz este proceso para cada base. Explica con palabras y/o muestra en un gráfico cada paso que diste y qué bloques tenías en cada paso. Indique el número exacto de cada tipo de bloque (s) que tenía cuando no había más intercambios por hacer. Por último, escribir la respuesta en la base solicitada en el espacio provisto. Revisa tu trabajo convirtiendo de nuevo a Base Diez. ¡Usa los modelos físicos (saca los bloques) para hacer estos problemas!
a. Base Dos ____
b. Base Tres ____
c. Base Cuatro ____
Si solo necesitábamos convertir números relativamente pequeños y siempre tuviéramos Bloques Base disponibles en cualquier base a la que necesitábamos convertir, podríamos seguir convirtiendo a varias bases usando los bloques y haciendo intercambios. Pero no siempre es así. Considera si te pidieron convertir 999 a Base Cuatro. Esto llevaría bastante tiempo y tedioso. Entonces, ahora exploraremos formas de convertir sin usar manipulativos.
Retrocedamos un paso considerando cómo, mediante el uso de manipuladores, obtuvimos la respuesta al ejercicio 2 de Ejercicio Set 3. Básicamente, convertimos el número 27 de Base Diez a un numeral Base Dos usando tazas (unidades), pintas (largas), cuartos (pisos), medio galones (bloques) y galones (bloques largos).
¿Cómo lo hicimos?
1. Empieza por enumerar con cuántas tazas comienzas. Ver abajo.
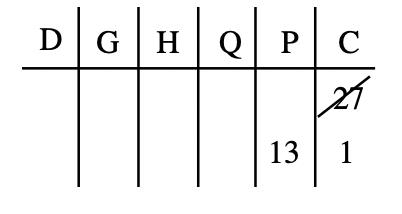
2. A continuación, para consolidar las copas en pintas, dividimos el número de tazas (27 en Base Diez) por 2 (porque estamos convirtiendo a base Dos) para obtener 13 pintas (el cociente) con 1 taza sobrante (el resto) cuando divides 27 por 2, 13 es el cociente y 1 es el resto. Entonces, ahora tenemos 13 pintas y 1 taza. Tachar 27 tazas y mostrar nuevo cociente y resto. Realice un seguimiento en un gráfico como se muestra a continuación.
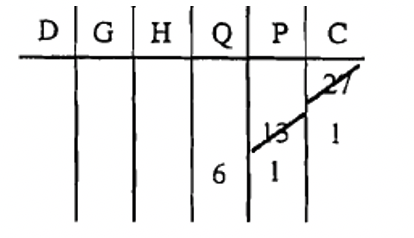
3. Para consolidar las pintas en cuartos, dividimos el número de pintas (13) por 2 (la base) lo que da 6 cuartos (el cociente) y 1 pinta sobrante (el resto). Tachar el 13 y mostrar nuevo cociente y resto. Ver abajo.
4. Para consolidar los cuartos en medio galones, dividimos el número de pintas (6) por 2 (la base) lo que da 3 medios galones (el cociente) y cero cuartos sobrantes. Vea a continuación cómo realizar un seguimiento.
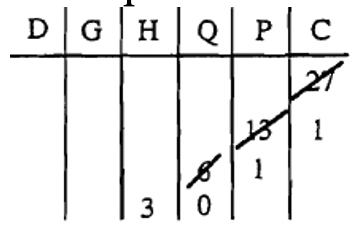
5. Para consolidar los medios galones en galones, dividimos el número de medio galones (3) por 2 (la base), dándonos 1 galón (el cociente) y 1 medio galón sobrante. Mantenga un registro como se muestra a continuación
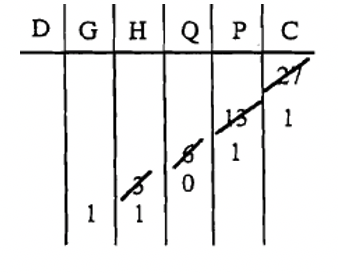
En este punto, no podemos consolidarnos más. Al hacer cada división, el resto siempre debe ser menor de lo que está dividiendo, que es la base. Una vez que obtienes un cociente que también es menor que la base, terminas de convertir el número a la base deseada. En este ejemplo, estábamos convirtiendo a la base dos. Por lo tanto, simplemente leemos la tabla anterior para obtener la respuesta de\(11011_{\text{two}}\).
Entonces,\(27 = 11011_{\text{two}}\).
El algoritmo (o método) anterior funciona para convertir cualquier número Base Diez a cualquier otra base. A continuación se presentan los pasos:
1. Comienza poniendo el número a convertir en el lugar de la unidad. Divide el número por la base. El nuevo cociente va en el siguiente valor posicional a la izquierda y el resto va en el lugar de la unidad.
2. Divide el cociente que acabas de obtener por la base. El nuevo cociente va en el siguiente valor posicional a la izquierda y el resto va en el lugar del viejo cociente.
3. Repita el paso 2 hasta que el cociente sea menor que la base. Ahora escribe el numeral en la base a la que te estabas convirtiendo. Recuerda escribir la base como un nombre de número (“dos”, "tres”, etc.) a la derecha del número!!!!! Por último, pero lo más importante, ¡COMPROBAR TU Respuesta convirtiendo de nuevo a un numeral Base Diez!
Si olvidaste cómo usar la calculadora para encontrar fácilmente el cociente y el resto al hacer problemas de división, mira hacia atrás en la página 18 del Conjunto de ejercicios 2 y vuelve a practicar el ejercicio 8. Registre cada cociente y resto de manera cuidadosa y organizada mientras trabaja en el problema. Entonces, al final del cálculo, es fácil escribir el numeral en la nueva base. Observe lo bien que esto funciona en los siguientes ejemplos.
Convierte 82 a Base Seis.
El gráfico donde hago un seguimiento está a continuación.
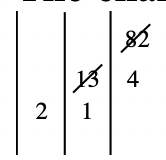
Mis cálculos fueron:
\(82 \div 6 = 13\)rem. \(\underline{4}\)
\(13 \div 6 = 2\)rem. \(\underline{1}\)
Desde el último cociente,\(\underline{2}\), fue menor que la base, 6, esto señalaba el fin del problema. Por lo que 82 como numeral en la Base Seis se registra como\(\mathbf{214}_{\mathbf{six}}\). Consulta para ver si\(214_{\text{six}}\) realmente es 82.
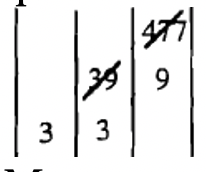
Convierte 477 a Base Cinco.
A continuación se muestra el gráfico donde hago un seguimiento de los cocientes/restos.
Mis cálculos fueron:
\(477 \div 5 = 95\)rem. \(\underline{2}\)
\(95 \div 5 = 19\)rem. \(\underline{0}\)
\(19 \div 5 = 3\)rem. \(\underline{4}\)
Por lo que 477 como un numeral en la Base Cinco se registra como\(\mathbf{3402}_{\mathbf{five}}\). Consulta para ver si\(3402_{\text{five}}\) realmente es 477.
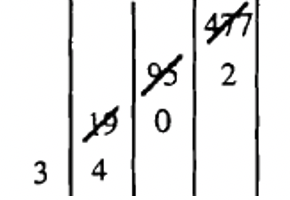
Convierte 477 a Base Doce.
A continuación se muestra el gráfico donde hago un seguimiento de los cocientes/restos.
Mis cálculos fueron:
\(477 \div 12 = 39\)rem. \(\underline{9}\)
\(39 \div 12 = 3\)rem. \(\underline{3}\)
Por lo que 477 como un numeral en la Base Doce se registra como\(\mathbf{339}_{\mathbf{twelve}}\). Consulta para ver si\(339_{\text{twelve}}\) realmente es 477.
Convierte 477 a Base Tres.
A continuación se muestra el gráfico donde hago un seguimiento de los cocientes/restos.
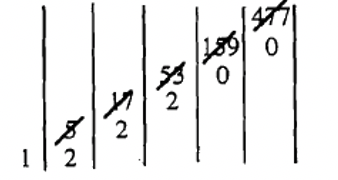
Mis cálculos fueron:
\(477 \div 3 = 159\)rem. \(\underline{0}\)
\(159 \div 3 = 53\)rem. \(\underline{0}\)
\(53 \div 3 = 17\)rem. \(\underline{2}\)
\(17 \div 3 = 5\)rem. \(\underline{2}\)
\(5 \div 3 = 1\)rem. \(\underline{2}\)
Por lo que 477 como un numeral en la Base Tres se registra como\(\mathbf{122200}_{\mathbf{three}}\). Consulta para ver si\(122200_{\text{three}}\) realmente es 477.
Estudie cuidadosamente los ejemplos anteriores antes de trabajar en el siguiente ejercicio. La clave es estar organizado en tu trabajo anotando cada paso del proceso.
Convierte cada número Base Diez a la base especificada y coloca una caja alrededor de tu respuesta. Después, comprueba tu respuesta convirtiendo la respuesta de nuevo a Base Diez.
| a. 200 a la Base Cuatro | b. 450 a la Base Siete |
| c. 89 a la Base Dos | d. 264 a la Base Tres |
| e. 320 a la Base Trece |
El algoritmo que hemos estado empleando debería tener sentido dada la forma en que convertimos a otras bases a partir de Base Diez usando los Bloques Base. Este método es bastante sencillo y no es necesario conocer los valores de posición reales a medida que llena los titulares de lugares. Tampoco sabes cuántos dígitos tendrá el número hasta que hayas terminado el problema. Existe otro método de conversión que ahora estudiaremos. Para este segundo método, determinamos y escribimos los valores de posición reales y calculamos el número de dígitos que tendrá el numeral como primer paso del problema.
\[ \begin{aligned} \frac{\mathbf{2}}{36} \frac{}{6} \frac{}{1} \\ \frac{\mathbf{2}}{36} \frac{\mathbf{1}}{6} \frac{}{1} \\ \frac{\mathbf{2}}{36} \frac{\mathbf{1}}{6} \frac{\mathbf{4}}{1} \end{aligned} \nonumber \]
Ahora convertiremos 82 a Base Six usando un nuevo algoritmo. Veremos el proceso de conversión de manera muy diferente. Primero, consideramos los valores posicionados en un numeral Base Seis. Ya que solo necesitamos subir hasta 82, no necesitamos mostrar un valor posicional mayor a 82. Nuestro primer paso es escribir una tabla del valor posicional para Base Seis con los valores positorios mostrados bajo espacios en blanco donde rellenaremos los dígitos para el numeral Base Seis. Esto se muestra a la derecha. Observe que esto será un número de tres dígitos. Partiendo de la izquierda, el primer dígito (en el lugar de los 36) indicará cuántos 36 hay en 82. Este es el problema de la división:\(82 \div 36 = 2\), rem. 10. Así, 2 será el primer dígito y tenemos 2 __ __ seis para nuestro número hasta el momento. Ahora tenemos que tomar el resto de 10 y hacer lo mismo para el siguiente valor posicional. Para determinar cuántos 6's hay en 10, hacemos este problema de división:\(10 \div 6 = 1\), rem. 4. Esto da un 1 para el siguiente dígito en el numeral, así que tenemos 2 1 __ seis y ya casi terminamos. Cuando estás abajo al lugar de las unidades, el resto va en el lugar de las unidades. Entonces 82 convierte a\(214_{\text{six}}\) lo que es la misma respuesta que obtuvimos cuando la calculamos usando el primer algoritmo. A la izquierda, puedes ver los tres pasos dados a medida que rellenas la tabla en tu camino a escribir la respuesta final en Base Seis. ¡Recuerda verificar la respuesta!
\[ \begin{aligned} \frac{\mathbf{3}}{125} \frac{}{25} \frac{}{5} \frac{}{1} \\ \frac{\mathbf{3}}{125} \frac{\mathbf{4}}{25} \frac{}{5} \frac{}{1} \\ \frac{\mathbf{3}}{125} \frac{\mathbf{4}}{25} \frac{\mathbf{0}}{5} \frac{}{1} \\ \frac{\mathbf{3}}{125} \frac{\mathbf{4}}{25} \frac{\mathbf{0}}{5} \frac{\mathbf{2}}{1} \end{aligned} \nonumber \]
Vamos a convertir 477 a Base Cinco usando este algoritmo. Primero determine los valores posicionados para la Base Cinco, señalando que no rellena los valores posicionados superiores a 477. Esto se muestra en la línea superior a la derecha. Ahora sabemos que hay cuatro dígitos en este número Base Cinco. El paso 1 es determinar cuántos 125 hay en 477 cual es el problema de división: 477 125 = 3, rem. 102. La secuencia de pasos para rellenar el numeral se muestra a la derecha. Observe el 3 en el primer valor posicional. A continuación, debemos determinar cuántos 25 hay en 102 (el resto). Espero que no necesites una calculadora para ésta. Hay 4, con un resto de 2. Entonces, 4 se llena en el lugar de los 25. Nos quedamos con un resto de 2 y como no hay 5's en 2, se pone un 0 en ese valor posicional. A continuación se encuentra el lugar de las unidades así que el 2 se deposita ahí. De ahí que la respuesta sea a\(3402_{\text{five}}\) cuál es exactamente a lo que llegamos al usar el primer algoritmo. ¡Asegúrate de recordar verificar la respuesta!
\[ \frac{}{128} \frac{}{64} \frac{}{32} \frac{}{16} \frac{}{8} \frac{}{4} \frac{}{2} \frac{}{1} \nonumber \]
Vamos a convertir 77 a un numeral Base Dos usando este algoritmo. Primero, mira algunos valores positorios de Base Dos que se muestran arriba. Los únicos dígitos en la Base Dos son 1's y 0's Realmente no tienes que hacer ningún problema de división. El primer dígito siempre será un 1 y estará en el valor posicional más alto que se pueda restar del número que estamos convirtiendo. 77 convierte a un numeral de siete dígitos con un 1 en el lugar de los 64 ya que 64 es el valor posicional más alto que se puede restar de 77. Coloca un 1 en ese valor posicional y resta (77 - 64 = 13). Toma el nuevo número, 13, y encuentra el siguiente valor posicional más alto del que se puede restar 13, poniendo un 0 en cualquier valor posicional mayor que 13. Esto obliga a un 0 en los siguientes dos puntos de valor posicional —32 y 16. Poner un 1 en el lugar de los 8's ya que es el valor posicional más alto que se puede restar de 13. Después de restar 8 de 13, tenemos 5. Pon un 1 en el lugar de los 4's ya que 4 se puede restar de 5, dejando un 1. Esto fuerza un 0 en el valor posicional para 2 y el resto de 1 va en el lugar de unidades.
A la izquierda hay una manera de hacer un seguimiento de cada resta realizada. Simplemente ponga un 1 en cada valor posicional restado (marcas de verificación de nota) y un cero para todos los demás valores posicionados. De ahí que la respuesta sea\(\mathbf{1001101}_{\mathbf{two}}\). Esto se comprueba fácilmente: 64 + 8 + 4 + 1 = 77.
Convierte el número Base Diez 155 a la base especificada usando el segundo algoritmo presentado.
| a. Base Tres | b. Base Doce |
| c. Base Dos | d. Base Cinco |
Usa cualquier algoritmo que prefieras para convertir 13595 a la base especificada. ¡MOSTRAR TRABAJO!
| a. Base Once | b. Base Trece |
Convertir 838 a la base especificada.
| a. Base Doce | b. Base Ocho |
| c. Base Siete | d. Base Nueve |
Ambos métodos mostrados para convertir un numeral Base Diez en una base diferente funcionan bien. Pero los enfoques son muy diferentes. Lo mejor es que ambos puedan entender y hacerlo de cualquier manera. Eventualmente, te conformarás en hacerlo de una manera sobre la otra. Durante años, solo lo hice usando el segundo algoritmo porque esa era la única forma en que supe hacerlo. Ahora, me parece más interesante el primer método. Sea cual sea la forma que elija convertir, es muy importante que revise su trabajo volviendo a la Base Diez.
Discutir las diferencias y ventajas de cada algoritmo utilizado para convertir un numeral Base Diez a una base diferente. ¿Qué método prefieres y por qué?
El último tema que exploraremos es cómo contar en bases distintas a la Base Diez. En otras palabras, ¿cómo podemos escribir una secuencia de contar números en una base dada sin convertir cada número de Base Diez uno a la vez? Además, aprenderás a tomar un numeral en una base dada y, sin ninguna conversión, declarar tanto el numeral anterior como el siguiente en esa misma base.
Comience por estudiar patrones en los números de conteo en la Base Diez. Empezaremos con cero aunque realmente no es un número de conteo. Leer a través de una fila a la vez.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
y así sucesivamente por un tiempo hasta que lleguemos a...
| 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 |
| 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 |
| 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 |
| 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 |
y de nuevo esto continúa por un tiempo hasta que lleguemos a...
| 980 | 981 | 982 | 983 | 984 | 985 | 986 | 987 | 988 | 989 |
| 990 | 991 | 992 | 993 | 994 | 995 | 996 | 997 | 998 | 999 |
| 1000 | 1001 | 1002 | 1003 | 1004 | 1005 | 1006 | 1007 | 1008 | 1009 |
y ya sabes cómo va esto y sigue y sigue, ¿verdad?
Aquí hay algunas cosas a las que prestar atención:
- El último dígito siempre cambia de un número al siguiente
- Al mirar a través de cada fila, solo el último dígito cambia de un número al siguiente
- Observe cuántos números se escriben en una fila antes de que más que solo el último dígito cambie de un número al siguiente
- Cuando cambia más del último dígito, anote el último dígito del número anterior y el último dígito del nuevo número
- Observe lo que se necesita para cambiar de un número de un dígito a un número de dos dígitos, de un número de dos dígitos a un número de tres dígitos, de un número de tres dígitos a un número de cuatro dígitos, etc.
- Observe el patrón de los primeros números de dos, tres o cuatro dígitos, etc.
En Base Diez, ¿cuántos números consecutivos puedes escribir en fila antes de tener que cambiar más de un dígito? ____
En Base Diez, ¿qué es cierto del numeral si cambia más que el último dígito cuando escribes el siguiente número? _____
En Base Diez, ¿cuál es el número de ocho dígitos más grande? ____
En Base Diez, ¿cuál es el número más pequeño de diez dígitos? ____
Estudia esta tabla de conteo en la Base Tres. Comienza con cero y cuenta hasta 95 que es\(10112_{\text{three}}\). Lee a través de cada fila y luego hacia abajo en la página. Intenta reconocer patrones similares a los que se encuentran en la Base Diez. Después, contesta las preguntas del lado derecho de la página.
| \(0_{\text{three}}\) | \(1_{\text{three}}\) | \(2_{\text{three}}\) |
| \(10_{\text{three}}\) | \(11_{\text{three}}\) | \(12_{\text{three}}\) |
| \(20_{\text{three}}\) | \(21_{\text{three}}\) | \(22_{\text{three}}\) |
| \(100_{\text{three}}\) | \(101_{\text{three}}\) | \(102_{\text{three}}\) |
| \(110_{\text{three}}\) | \(111_{\text{three}}\) | \(112_{\text{three}}\) |
| \(120_{\text{three}}\) | \(121_{\text{three}}\) | \(122_{\text{three}}\) |
| \(200_{\text{three}}\) | \(201_{\text{three}}\) | \(202_{\text{three}}\) |
| \(210_{\text{three}}\) | \(211_{\text{three}}\) | \(212_{\text{three}}\) |
| \(220_{\text{three}}\) | \(221_{\text{three}}\) | \(222_{\text{three}}\) |
| \(1000_{\text{three}}\) | \(1001_{\text{three}}\) | \(1002_{\text{three}}\) |
| \(1010_{\text{three}}\) | \(1011_{\text{three}}\) | \(1012_{\text{three}}\) |
| \(1020_{\text{three}}\) | \(1021_{\text{three}}\) | \(1022_{\text{three}}\) |
| \(1100_{\text{three}}\) | \(1101_{\text{three}}\) | \(1102_{\text{three}}\) |
| \(1110_{\text{three}}\) | \(1111_{\text{three}}\) | \(1112_{\text{three}}\) |
| \(1120_{\text{three}}\) | \(1121_{\text{three}}\) | \(1121_{\text{three}}\) |
| \(1200_{\text{three}}\) | \(1201_{\text{three}}\) | \(1202_{\text{three}}\) |
| \(1210_{\text{three}}\) | \(1211_{\text{three}}\) | \(1212_{\text{three}}\) |
| \(1220_{\text{three}}\) | \(1221_{\text{three}}\) | \(1222_{\text{three}}\) |
| \(2000_{\text{three}}\) | \(2001_{\text{three}}\) | \(2002_{\text{three}}\) |
| \(2010_{\text{three}}\) | \(2011_{\text{three}}\) | \(2012_{\text{three}}\) |
| \(2020_{\text{three}}\) | \(2021_{\text{three}}\) | \(2022_{\text{three}}\) |
| \(2100_{\text{three}}\) | \(2101_{\text{three}}\) | \(2102_{\text{three}}\) |
| \(2110_{\text{three}}\) | \(2111_{\text{three}}\) | \(2112_{\text{three}}\) |
| \(2120_{\text{three}}\) | \(2121_{\text{three}}\) | \(2122_{\text{three}}\) |
| \(2200_{\text{three}}\) | \(2201_{\text{three}}\) | \(2202_{\text{three}}\) |
| \(2210_{\text{three}}\) | \(2211_{\text{three}}\) | \(2212_{\text{three}}\) |
| \(2220_{\text{three}}\) | \(2221_{\text{three}}\) | \(2222_{\text{three}}\) |
| \(10000_{\text{three}}\) | \(10001_{\text{three}}\) | \(10002_{\text{three}}\) |
| \(10010_{\text{three}}\) | \(10011_{\text{three}}\) | \(10012_{\text{three}}\) |
| \(10020_{\text{three}}\) | \(10021_{\text{three}}\) | \(10022_{\text{three}}\) |
| \(10100_{\text{three}}\) | \(10101_{\text{three}}\) | \(10102_{\text{three}}\) |
| \(10110_{\text{three}}\) | \(10111_{\text{three}}\) | \(10112_{\text{three}}\) |
En Base Tres, ¿cuántos números consecutivos puedes escribir en fila antes de tener que cambiar más de un dígito?
En Base Tres, ¿qué es cierto del numeral si cambia más que el último dígito cuando escribes el siguiente número?
En Base Tres, ¿cuál es el número de siete dígitos más pequeño?
En Base Tres, ¿cuál es el número de siete dígitos más grande?
Para cada número Base Tres, escriba el siguiente número consecutivo:
| a.\(1 \ 202 \ 010_{\text{three}}\): |
| b.\(2 \ 220 \ 011_{\text{three}}\): |
| c.\(1 \ 010 \ 102_{\text{three}}\): |
| d.\(2 \ 100 \ 212_{\text{three}}\): |
| e.\(2 \ 120 \ 222_{\text{three}}\): |
Para cada número Base Tres, escriba el número que lo precede:
| a.\(1 \ 200 \ 102_{\text{three }}\) |
| b.\(1 \ 202 \ 221_{\text{three}}\) |
| c.\(2 \ 110 \ 020_{\text{three}}\) |
| d.\(2 \ 110 \ 100_{\text{three}}\) |
¿Qué hay de malo con el número,\(1 \ 022 \ 301_{\text{three}}\)
Comenzando con cero, cuente hasta 23 en Base Cuatro rellenando los números faltantes.. Contar a lo largo de cada fila como se hizo en la Base Diez y la Base Tres.
| \(0_{\text{four}}\) | \(2_{\text{four}}\) | \(3_{\text{four}}\) | |
| \(11_{\text{four}}\) | |||
| \(20_{\text{four}}\) | \(23_{\text{four}}\) | ||
| \(112_{\text{four}}\) |
Verifique escogiendo un número aleatorio en la lista. Toma\(112_{\text{four}}\) de la lista anterior. Desde que empezaste a contar desde cero, ese numeral debería ser el mismo que\(22_{\text{ten}}\), que es a lo que se\(112_{\text{four}}\) convierte en Base Diez. Siempre revisa el último número también. En este caso, el último numeral debería convertirse a 23. A lo mejor se le pide contar de 121 a 135 en Base Cinco. El primer paso sería convertir 121 a un numeral Base Cinco, que es\(441_{\text{five}}\). Después, comience a contar escribiendo cada número sucesivo. Se listan los quince números:
\(441_{\text{five}}, 442_{\text{five}}, 443_{\text{five}}, 444_{\text{five}}, 1000_{\text{five}}, 1001_{\text{five}}, 1002_{\text{five}}, 1003_{\text{five}}, 1004_{\text{five}}, 1010_{\text{five}}, 1011_{\text{five}}, 1012_{\text{five}}, 1013_{\text{five}}, 1014_{\text{five}}, 1020_{\text{five}}\)
Para verificar, tomar un numeral aleatorio en el medio\(1003_{\text{five}}\),, convertirlo y encontrarlo es 128. En la secuencia, debe ser igual a 128. Entonces, reviso el último número\(1020_{\text{five}}\) y me aseguro de que se convierta a 135, lo que hace. Esto indica que probablemente el resto también son correctos.
Cuenta de 1 a 20 en Base Dos
Cuenta de 61 a 68 en Base Ocho
Para cada numeral, escribe el numeral que le precede y también, su sucesor. ¡Intenta hacerlo sin convertir! Después, puedes convertir para comprobarlo
| a. ____,\(3027_{\text{eight}}\), ____ | ||
| b. ____,\(1240_{\text{five}}\), ____ | ||
| c. ____,\(101100_{\text{two}}\), ____ |
Por cada base dada, asuma que tenías el número designado de bloques, pisos, largos y/o unidades. Afirma cómo escribir el numeral en esa base y también en la base diez.
a. Base Tres: 4 bloques, 5 pisos, 1 largo y 4 unidades
b. Base Ocho: 19 pisos, 7 largos y 13 unidades
c. Base Cinco: 1 bloque, 13 largos y 15 unidades


