3.5: Algoritmos de resta
- Page ID
- 113202
Necesitarás: Bloques Base (Tarjetas de Material 4-15)
El algoritmo de resta más común es el Algoitmo de Resta Estándar de Derecha a Izquierda, que es donde comienzas en la columna unos y restas, luego te mueves hacia la izquierda y restas en cada columna. El problema, por supuesto, es cuando el dígito superior es menor que el dígito inferior y hay que reagruparse. Saca ya tus bloques Base Ten para ver qué está pasando realmente.
Considera el problema de la resta 425 —158. Por nuestro conocimiento del valor posicional, sabemos que 425 es 4\(\times\) 100 + 2\(\times\) 10 + 5 (o 400 + 20 + 5) y 158 es 1\(\times\) 100 + 5\(\times\) 10 + 8 (o 100 + 50 + 8). Usando bloques Base Diez, 425 se representarían con 4 pisos, 2 largos y 5 unidades, mientras que 158 se representarían con 1 plano, 5 largos y 8 unidades. Entonces, el problema de la resta puede pensarse de la siguiente manera:
Uso de bloques de base\[\begin{aligned} (4 \text{ flat(s) } + 2 \text{ long(s) } + 5 \text{ unit(s) }) \\ \underline{– (1 \text{ flat(s) } + 5 \text{ long(s) } + 8 \text{ unit(s) })} \end{aligned} \nonumber \]
Usando bloques, el problema de resta se muestra a continuación:
No podemos restar 8 unidades de 5 unidades, por lo que un largo se cambia por diez unidades, lo que da 4 pisos, 1 largo y 15 unidades en el minuendo. Ahora, tampoco podemos restar 5 largos de 1 largo, por lo que 1 piso se cambia por diez largos, lo que da 3 pisos, 11 largos y 15 unidades en el minuendo. Ahora podemos restar en cada columna, que se muestra en la página siguiente. Puedes usar el enfoque take away o el enfoque de adiciones faltantes para restar. Usa tus bloques base para resolver estos problemas.
Uso de bloques de base\[\begin{aligned} &(3 \text{ flat(s) } + 11 \text{ long(s) } + 15 \text{ unit(s)}) \\ -& (1 \text{ flat(s) } + 5 \text{ long(s) } + 8 \text{ unit(s)}) \\ \hdashline &2 \text{ flat(s) } + 6 \text{ long(s) } + 7 \text{ unit(s)}) = \underline{267} \end{aligned} \nonumber \]
El problema de resta usando bloques se muestra a continuación:
Ya que estamos trabajando en Base Diez, la respuesta (diferencia) es 267. Entonces, 425 —158 = 267.
El problema se puede trabajar usando un gráfico donde queda suficiente espacio entre el minuendo y el sustraendo para que los intercambios se puedan hacer en el minuendo. Observe los pasos que se muestran si trabaja este problema usando un gráfico base como se muestra a continuación.
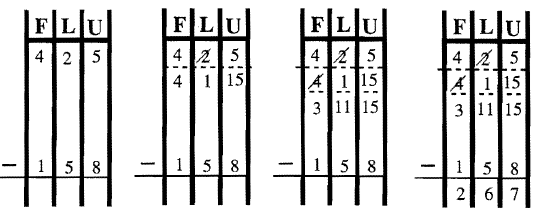
Ahora, realizaremos este algoritmo básico en diferentes bases. ¡Presta atención a la base cuando restes! Por ejemplo, en el primer ejemplo a continuación hay que cambiar un piso por 9 largos más (ya que es Base Nueve). Una forma de mostrar esto es agregar realmente 9 (la base) a la cantidad de largos que ya están ahí, así que taché el 5, y agrego 9 para obtener 14. Si lo escribes de esa manera, recuerda que el número que estás escribiendo está en Base Diez y no en la Base en la que estás trabajando. Escribirlo de esta manera probablemente sea más fácil cuando empiezas a restar por primera vez. Una forma más elegante es escribirla de la misma manera que lo haces cuando trabajas en Base Diez, que es poniendo un 1 delante del 5 en la columna longs para que parezca 15 (no significa quince), que en Base Nueve representa ¡14 longs (5 longs + 9 más del intercambio)! Se muestran ambas formas de escribirlo. Es posible que desee usar sus Bloques Base para ayudar a visualizar los intercambios reales que se están realizando. Estudia los siguientes ejemplos. Comprueba cada respuesta sumando la respuesta al sustraendo y ¡mira que obtienes el minuendo!
| \(\begin{aligned} 253_{\text{nine}} \\ \underline{-182_{\text{nine}}} \end{aligned}\) |  |
 |
 |
| \(\begin{aligned} 3\text{E}1_{\text{twelve}} \\ \underline{-14\text{T}_{\text{twelve}}} \end{aligned}\) |  |
 |
 |
| \(\begin{aligned} 402_{\text{five}} \\ \underline{-233_{\text{five}}} \end{aligned}\) |  |
 |
 |
| \(\begin{aligned} 1010_{\text{two}} \\ \underline{-111_{\text{two}}} \end{aligned}\) |  |
 |
 |
Comprobar:\(\begin{aligned} 11_{\text{two}} \\ \underline{+111_{\text{two}}} \\ 1010_{\text{two}} \end{aligned}\)
En los Ejemplos 3 y 4, cuando necesitaba hacer un intercambio y había un cero en el valor posicional a la izquierda, el intercambio tenía que hacerse primero a un valor posicional superior. Entonces, los intercambios se realizan en la línea hasta que se puede restar. Este caso ocurre en Base Diez todo el tiempo cuando restas un número de 100, 1000, 10000, etc. la mayoría de la gente simplemente empieza a tachar cada cero y poner 9's por encima de ellos por costumbre, sin tener idea de por qué lo están haciendo. Para restar 235 de 1000, primero debes tachar el 1, poner un cero por encima de él y poner un 1 frente al cero en el lugar de los cien (que está cotizando en 1000 por 10 cientos), luego debes tachar ese 10 en el lugar de los cien, poner un 9 por encima de él y poner un 1 frente al cero en el lugar de los diez (que está intercambiando 10 cientos por 9 cientos y 10 decenas), entonces deberías tachar ese 10, poner un 9 encima de él y un 1 frente al cero en el lugar del uno (que es intercambiar 10 decenas por 9 decenas y 10 unas). Entonces, se puede restar como se muestra en el ejemplo a la derecha. Es importante entender realmente lo que está pasando aquí porque los niños suelen pasar un momento muy difícil cuando hay un cero que tachar.
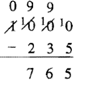
Realice los siguientes problemas de resta. Puedes usar bloques o gráficos para ayudar a visualizar el problema, pero eventualmente quieres trabajar para poder hacerlos sin los manipuladores. Debajo de cada problema, verifique sumando la diferencia (respuesta) al sustraendo (número que se resta) y vea si la suma es el minuendo (el número en la parte superior). Usa cualquier algoritmo de adición que prefieras.
| a.\(\begin{aligned} 4 5 2_{\text{thirteen}} \\ \underline{-1 3 \text{E}_{\text{thirteen}}} \end{aligned}\) | b.\(\begin{aligned} 8 3 1_{\text{nine}} \\ \underline{-6 7 0_{\text{nine}}} \end{aligned}\) | c.\(\begin{aligned} 2 0 0 4_{\text{six}} \\ \underline{-3 3 5_{\text{six}}} \end{aligned}\) | d.\(\begin{aligned} 4 2 1_{\text{five}} \\ \underline{-2 3 2_{\text{five}}} \end{aligned}\) | e.\(\begin{aligned} 1 0 0_{\text{three}} \\ \underline{-1 1_{\text{three}}} \end{aligned}\) |
Consulta cada problema aquí:
| a. | b. | c. | d. | e. |
El algoritmo tradicional de resta estándar no es necesariamente el mejor y hay muchos otros que aprenderás en el resto de este conjunto de ejercicios.
El siguiente algoritmo fue enseñado a mucha gente antes de las “nuevas matemáticas” y así lo llamo el Algoritmo de Oldtimer. Es similar al Algoritmo Estándar en que comienzas por la derecha y te mueves hacia la izquierda. Pero no se reagrupa (formalmente conocido como préstamo). Primero, vuelva a mirar un ejemplo de uso del Algoritmo Estándar para restar 95 — 28. Ya que, no se puede restar 8 de 5, se reagrupa del 9 tachando el 9 y escribiendo 8 para que pueda poner un 1 frente al 2. Ahora, en la columna de la unidad, 15 — 8 = 7 y en la columna de los diez, 8 — 2 = 6. La respuesta es 67. Este nuevo método comienza de la misma manera. No se puede restar 8 de 5, pero en vez de reagruparse del 9, se suma un 1 al número debajo del 9, y se pone un 1 delante del 5. Observe que en la columna de la unidad, 15 — 8 = 7 y en la columna de diez, en lugar de 8 —2, tiene 9 —3 que es la misma respuesta de 6. La ventaja de este método es que si pones un 1 en la parte superior de una columna, compensas agregando un 1 a la parte inferior de la siguiente columna. No tienes que preocuparte por tachar las cosas y hacer un lío y no tienes que pensar en el dígito en la columna de la izquierda hasta que vayas a esa columna a restar — ¡sin intentar reagruparte y colgarte ahí arriba! Mira los dos métodos uno al lado del otro. Si usas el nuevo método, tienes que dejar espacio entre la barra de sustracción y sustracción en caso de que necesites poner un 1 ahí.
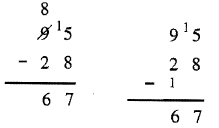
Lo que realmente me gusta del método Oldtimer es que es mucho más fácil de verificar. Basta con sumar cada columna. No hay acarreo: 7 + 8 = 15 y 6 + 1 + 2 = 9. Es una brisa. Para verificar el Algoritmo Estándar, bueno es algo de un desastre y tendrías que escribirlo en otro lugar y verificarlo. Estudia los siguientes ejemplos.
Aún hay que tener mucho cuidado para prestar mucha atención a la base. Cuando pones un 1 delante de un dígito, recuerda que representa el número que es la base. Otra forma de indicar lo mismo es escribir lo que representa como se muestra a continuación. Los mismos cinco ejemplos se ilustran nuevamente haciéndolo de esta manera. No es tan elegante pero si ayuda a llevar a casa lo que realmente está pasando, hazlo de esta manera.
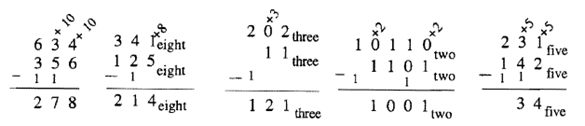
Resta lo siguiente usando el Algoritmo de Oldtimer. Revisa tus respuestas sumando.
| a.\(\begin{aligned} 5 0 3 6 \\ \underline{-3 4 1 8} \end{aligned}\) | b.\(\begin{aligned} 314_{\text{four}} \\ \underline{-221_{\text{four}}} \end{aligned}\) | c.\(\begin{aligned} 5 \text{T} 2_{\text{twelve}} \\ \underline{-2 3 \text{E}_{\text{twelve}}} \end{aligned}\) | d.\(\begin{aligned} 4 1 3_{\text{six}} \\ \underline{-3 2 4_{\text{six}}} \end{aligned}\) | e.\(\begin{aligned} 1 1 0 0_{\text{two}} \\ \underline{-1 0 1_{\text{two}}} \end{aligned}\) |
| f.\(\begin{aligned} 537_{\text{nine}} \\ \underline{-273_{\text{nine}}} \end{aligned}\) | g.\(\begin{aligned} 312_{\text{five}} \\ \underline{-224_{\text{five}}} \end{aligned}\) | h.\(\begin{aligned} 502_{\text{seven}} \\ \underline{-235_{\text{seven}}} \end{aligned}\) | i.\(\begin{aligned} 200_{\text{three}} \\ \underline{-121_{\text{three}}} \end{aligned}\) | j.\(\begin{aligned} 523_{\text{eight}} \\ \underline{-265_{\text{eight}}} \end{aligned}\) |
Ahora que has dominado ese algoritmo, aquí tienes otro para ti. Este es un Algoritmo de Izquierda a Derecha donde no se lleva a cabo ningún reagrupamiento hasta el final del problema — ¡se reagrupa de la respuesta! Así es como funciona. Comienza con la columna más a la izquierda y resta. Pasar a la siguiente columna. Restar si es posible. Si necesitas reagruparte, pon un 1 delante del dígito superior como de costumbre, y pon una barra a través del dígito anterior en la respuesta. Al final te quitarás la respuesta. Continúa a la siguiente columna hasta que hayas hecho la columna de la unidad. Después regresa y resta uno de todos los dígitos con un corte a través de ellos. Estudia el siguiente ejemplo el cual se muestra paso a paso.
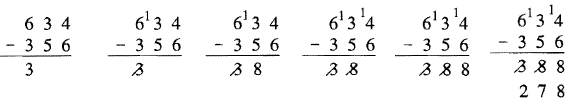
Aquí algunos ejemplos en otras bases. Si lo prefieres, en lugar de poner el 1 delante del dígito cuando te reagrupes, puedes poner, por ejemplo, +4 si está en Base Cuatro, como se mostró para el algoritmo anterior en la parte inferior de la última página.
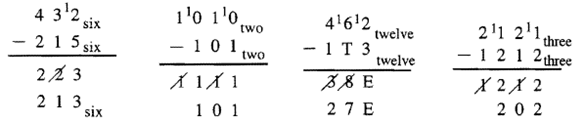
Consulta los ejemplos anteriores haciendo los siguientes problemas de adición.
| \(\begin{aligned} 213_{\text{six}} \\ \underline{+215_{\text{six}}} \end{aligned}\) | \(\begin{aligned} 101_{\text{two}} \\ \underline{+101_{\text{two}}} \end{aligned}\) | \(\begin{aligned} 2 7 \text{E}_{\text{twelve}} \\ \underline{+1 \text{T} 3_{\text{twelve}}} \end{aligned}\) | \(\begin{aligned} 202_{\text{three}} \\ \underline{+1212_{\text{three}}} \end{aligned}\) |
Resta lo siguiente usando el Algoritmo de Izquierda a Derecha.
| a.\(\begin{aligned} 8 0 4 2 \\ \underline{-1 3 2 5} \end{aligned}\) | b.\(\begin{aligned} 4132_{\text{five}} \\ \underline{-2413_{\text{five}}} \end{aligned}\) | c.\(\begin{aligned} 7210_{\text{eight}} \\ \underline{-5564_{\text{eight}}} \end{aligned}\) | d.\(\begin{aligned} \text{T} 3 7_{\text{thirteen}} \\ \underline{-569_{\text{thirteen}}} \end{aligned}\) | e.\(\begin{aligned} 1 1 0 1_{\text{two}} \\ \underline{-1 1_{\text{two}}} \end{aligned}\) |
Consulta las respuestas al Ejercicio 4 haciendo el problema de adición correspondiente
En este algoritmo, hay un pequeño detalle más. Si tachas un cero, debes continuar tachando el dígito a la izquierda del cero. Si hay más de un cero en fila a medida que vas a la izquierda, cruza cada cero hasta llegar a un dígito distinto de cero. Después, resta 1 de cada número tachado como antes. Presta atención a la base: En el segundo ejemplo a continuación, el número antes de 40five es 34five. En el tercer ejemplo, el número antes de 100two es 11two. Estudia los siguientes ejemplos.
Resta lo siguiente usando el Algoritmo de Izquierda a Derecha.
| a.\(\begin{aligned} 8 0 4 2 \\ \underline{-1 3 4 5} \end{aligned}\) | b.\(\begin{aligned} 4132_{\text{five}} \\ \underline{-2433_{\text{five}}} \end{aligned}\) | c.\(\begin{aligned} 7210_{\text{eight}} \\ \underline{-5214_{\text{eight}}} \end{aligned}\) | d.\(\begin{aligned} \text{T} 3 7_{\text{thirteen}} \\ \underline{-539_{\text{thirteen}}} \end{aligned}\) | e.\(\begin{aligned} 1 1 0 0_{\text{two}} \\ \underline{-10 1_{\text{two}}} \end{aligned}\) |
Consulta las respuestas al Ejercicio 6 haciendo el problema de adición correspondiente.
El álgebra te ayudará a entender el siguiente algoritmo:
M — S = M — S + x — x = M + x — S — x = (M + x) — (S + x)
M — S = M — S + x — x = M — x — S + x = (M —x) — (S — x)
Básicamente, esto establece que para restar dos números, M (minuend) y S (restar), obtienes la misma respuesta si primero sumas (o restas) el mismo número tanto a M como a S antes de restar. El Algoritmo de Oldtimer funciona debido a este hecho. Por ejemplo, cuando pones un 1 delante del dígito de la unidad del minuendo y un 1 por debajo del dígito del diez del sustraendo, estás sumando tanto un 10 al minuendo como al sustraendo; entonces, restas.
Este algoritmo es particularmente útil si el minuendo tiene una cadena de ceros al final. Restar 1 del minuendo y restando primero y luego hacer la resta. Mira cómo funciona esto:
| \(\begin{aligned} 100000 && && 99999 \\ \underline{–65378} && && \underline{–65377} \\ 34622 &&= && 34622 \end{aligned}\) | \(\begin{aligned} 3000 && && 2999\\ \underline{–1264} && && \underline{–1263} \\ 1736 && = && 1736 \end{aligned}\) |
Bueno, ¿qué opinas? ¿No es más fácil hacer la segunda resta que se muestra en cada par que la primera? ¡Acabo de restar 1 del minuendo y restando primero!
Haz dos de tus propios problemas de resta usando este método para restar.
Este algoritmo también funciona bien si el sustraendo está cerca de una potencia de la base, como 100, 1000, etc. Por ejemplo, para el problema de resta 4503 — 997, sumar 3 al minuendo y restando para que el problema se convierta en 4506 — 1000 = 3506. En el problema Base Cuatro,\(2302_{\text{four}} – 333_{\text{four}}\), agrega 1 a ambos para obtener\(2303_{\text{four}} – 1000_{\text{four}} = 1303_{\text{four}}\)
Haz dos de tus propios problemas de resta usando este método para restar. Use una base que no sea 10.
El método anterior se denomina a veces el Método Complementario. Todavía hay un enfoque más específico llamado Algoritmo Complementario. Se basa en la idea de complementos que definimos en un conjunto de ejercicios anterior. En Base Diez, los pares de complementos fueron 1 y 9, 2 y 8, 3 y 7, 4 y 6 y 5 y 5. Para el método complementario, encuentras un complemento muy específico del sustraendo y sumarlo tanto al minuendo como al sustraendo antes de restarlo. El complemento, en este caso, es un 1 seguido sólo de ceros de tal manera que el número de ceros es el mismo número de dígitos en el minuendo. Primero, tendrás que idear una manera fácil de encontrar el complemento de un número determinado.
A continuación se muestran ejemplos que muestran cómo encontrar el complemento (C) de un número dado (A), dado que desea que A + C sume hasta un número B.
A = 74 y B = 1000.
Solución
Para encontrar C, agregue 6 a 74 para obtener 80, luego 20 para obtener 100 y 900 para obtener 1000. C = 926.
A =\(24_{\text{six}}\) y B =\(1000_{\text{six}}\).
Solución
Para encontrar C, agregue 2 unidades para obtener 3 largos, luego 3 largos para obtener 1 piso y 5 pisos para obtener 1 cuadra. Entonces C =\(532_{\text{six}}\).
Hay otras formas de averiguar el complemento. Por ejemplo, en Base Diez, si A es 28403 y quieres una C tal que A + C = 1000000, puedes encontrar la respuesta escribiendo el complemento real de 3, que es 7, para el dígito de la unidad. Muévete a la izquierda. Se quiere un dígito por cada valor posicional que cuando se suma al dígito dé una suma de 9. Haz esto hasta que el número tenga tantos dígitos como ceros haya en 1000000. En este caso, la respuesta es 971597. ¡Es más difícil de explicar que hacerlo! Si tienes tu propia forma de averiguar el complemento, ¡eso es genial! No lo guardes en secreto.
Encuentra el complemento (C) del número dado (A) tal que A + C = B.
a. A = 538 y B = 10000
b. A =\(212_{\text{four}}\) y B =\(1000_{\text{four}}\)
c. A =\(1011_{\text{two}}\) y B =\(10000_{\text{two}}\)
Así es como funciona este método complementario. Considerar el problema 452 — 74. Necesitamos encontrar el número que cuando se agrega al 74 es 1000. ¿Cómo eliges a qué debe sumar, como en 1000? Si el primer número (minuendo) es un número de 2 dígitos, desea un 1 con 2 ceros (100). Si el primer número (minuendo) es un número de 3 dígitos, desea un 1 con 3 ceros (1000), y así sucesivamente. Este paso es el mismo en todas las bases. Volver al problema: 452 — 74:926 es lo que se debe agregar al 74 para obtener 1000 (del Ejemplo 1). Sumar 926 al minuendo y restando para obtener el nuevo problema de resta que es: 1378 — 1000 = 378. La respuesta es el nuevo minuendo sin el primer dígito: 378. ¡Bastante salvaje! Mira\(402_{\text{six}} –24_{\text{six}}\). Necesitamos encontrar el número que cuando se agrega a\(24_{\text{six}}\) es\(1000_{\text{six}}\)., que es\(532_{\text{six}}\) del Ejemplo 2. \(532_{\text{six}}\)Sumar al minuend y restar para obtener el nuevo problema de resta que es\(1304 – 1000_{\text{six}} = 304_{\text{six}}\). Nuevamente, la respuesta es el nuevo minuend sin el primer dígito:\(304_{\text{six}}\). Entonces aquí está el truco — ¡Solo agrega el complemento al minuend, quítate el primer dígito y esa es la respuesta! No hay sustracción.
Restar usando el método complementario: 912 — 573
Solución
427 es el número que cuando se suma a 573 equivale a 1000. Agregar al minuendo: 427 + 912 = 1339. Quítate el primer dígito y la respuesta es 339.
Restar\(301_{\text{four}} – 212_{\text{four}}\) usando el algoritmo complementario.
Solución
A partir de 10.b., el complemento es\(122_{\text{four}}\). \(301_{\text{four}} + 122_{\text{four}} = 1023_{\text{four}}\).
Entonces la respuesta es\(23_{\text{four}}\).
Restar\(1100_{\text{two}} – 1011_{\text{two}}\) usando el algoritmo complementario y su respuesta de 10.c.
Realizar los siguientes problemas de resta utilizando el método complementario.
| a.\(\begin{aligned} 5034 \\ \underline{–357} \end{aligned}\) | b.\(\begin{aligned} 420_{\text{five}} \\ \underline{–231_{\text{five}}} \end{aligned}\) |
El método complementario es en realidad más fácil de hacer con los bloques, una vez que lo dominas. Saca tus bloques Base Tres para hacer el siguiente ejemplo y problemas.
Para computar\(212_{\text{three}} – 120_{\text{three}}\), representar\(212_{\text{three}}\) y\(120_{\text{three}}\) con los bloques como se muestra a continuación.
El minuendo se muestra a la izquierda. Dado que su “bloque” más grande es un piso, el siguiente “valor posicional” hasta una cuadra. Entonces el problema es averiguar qué hay que sumar al sustraendo (mostrado a la derecha) para hacer un bloque. Sería 1 más largo y 1 más plano. Es decir, si añadías un largo y plano al sustraendo, tendrías un bloque, ¿verdad? Agrega esa misma cantidad al minuendo, que se muestra a la izquierda arriba. Debería verse así:
Si restas ahora, la respuesta es el nuevo minuendo con el bloque más grande eliminado. Por lo tanto, la respuesta es 2 largos y 2 unidades, o\(22_{\text{three}}\) El paso crucial es averiguar qué es lo que hay que sumar al sustraendo para hacer el bloque. Entonces, agréguelo también al minuend, retire el bloque más grande del nuevo minuend y ¡esa es la respuesta! ¡Ta da!
Dado que dibujar los bloques a veces es engorroso, otra forma de mostrar pictóricamente lo que está sucediendo es usar imágenes abreviadas para la Base Tres bloques, pisos, largos y unidades (3B, 3F, 3L, U) como se muestra a continuación.
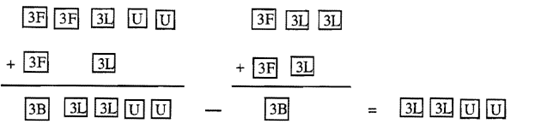
En la página siguiente, utilice los bloques base apropiados para restar\(120_{\text{three}} - 12_{\text{three}}\) y\(213_{\text{four}} - 133_{\text{four}}\) utilizando el método complementario. Explique cómo hacerlo y mostrar imágenes completas o abreviadas con los bloques base.
a. Utilizar Base Tres Bloques y método complementario para restar\(120_{\text{three}} – 12_{\text{three}}\).
b. Utilizar Base Cuatro Bloques y método complementario para restar\(213_{\text{four}} – 133_{\text{four}}\).
Explique cómo está haciendo cada alumno el problema de resta 634 — 152.
a. María hace la resta en su cabeza pensando en voz alta “534, 484, 482". ¿Cuál es su razonamiento?
b. Pedro hace la resta pensando en voz alta "634 y 48 es 682, llevar 200 es 482". ¿Cuál es su razonamiento?
Otro método para restar se llama el Algoritmo Restar del Base. Este es especialmente agradable para trabajar en otras bases. En este método nunca es necesario restar de un número mayor que la base.
Algoritmo estándar:
| \(\begin{aligned} 534 \\ \underline{-256} \end{aligned}\)hacer intercambios\(\begin{aligned} {}^{4}&& {}^{12} &&{}^{14} \\ \cancel{5} &&\cancel{3}&&4 \\ -2&&5&&6 \\ \hline 2&&7&&8 \end{aligned}\) |
Usando el método Restar de la base si tienes un lugar donde el número inferior es mayor que el número superior, reagrupa como en el método tradicional luego resta el número inferior de la base y suma el resultado al número superior. La ventaja de este método es que nunca restas un número de ningún número mayor que la base. Este es un buen método para las personas que necesitan usar los dedos para restar.
Restar del algoritmo base:
Al usar este método en otras bases, circule el número base cuando se reagrupe. Por ejemplo cuando se trabaja en base seis, 6 no existe y escribir 10 puede resultar confuso aunque sea correcto.
Resta lo siguiente usando el Algoritmo Restar del Base. Estos son los mismos problemas de #6. No olvides rodear el número base cuando se reagrupe.
| a.\(\begin{aligned} 8 0 4 2 \\ \underline{-1345} \end{aligned}\) | b.\(\begin{aligned} 4 1 3 2_{\text{five}} \\ \underline{-2433_{\text{five}} } \end{aligned}\) | c.\(\begin{aligned} 7 2 1 0_{\text{eight}} \\ \underline{ -5214_{\text{eight}}} \end{aligned}\) | d.\(\begin{aligned} \text{T} 3 7_{\text{thirteen}} \\ \underline{ -539_{\text{thirteen}}} \end{aligned}\) | e.\(\begin{aligned} 1 1 0 0_{\text{two}} \\ \underline{-101_{\text{two}} } \end{aligned}\) |
¿Conoces otro algoritmo para suma o resta? Si es así, publícalo con una explicación en el Foro para obtener crédito extra.