3.4: Resta
- Page ID
- 113209
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Necesitarás: Una Calculadora, Bloques Base (Tarjetas de Material 4-15) Tiras en C (Tarjetas de Material 16A-16L)
¿Cómo usarías el manipulador para explicarle cómo le restas a un niño pequeño?
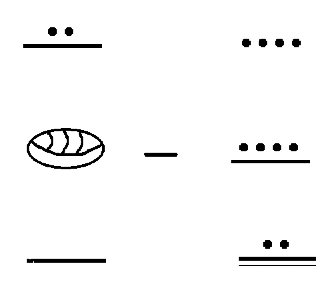
Hay dos enfoques distintos para la resta. El que la mayoría de nosotros conocemos es el Método para Llevar. Una forma típica de que alguien pueda introducir la idea de sustracción es diciendo “Si pongo cinco manzanas en el bol y luego me llevo dos de las manzanas, ¿cuántas quedan en el tazón?” La siguiente ilustración muestra esto como un problema de resta donde después de retirar dos manzanas del tazón, quedan tres manzanas.
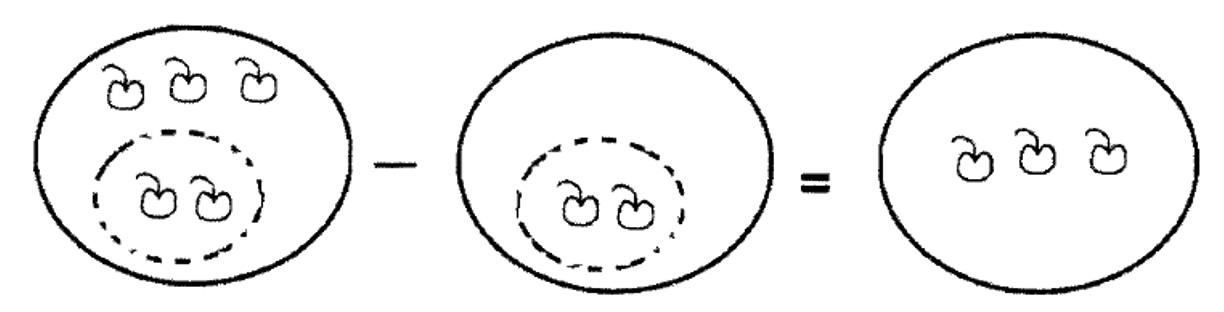
El problema anterior ilustra el enfoque para llevar a la resta.
Vocabulario de resta: Para x — y = z, x se llama el minuendo, y se llama sustraendo, y z (la respuesta) se llama la diferencia.
Para el problema de la resta 7 — 3, Indique el
Si B es un subconjunto de A, entonces n (A) — n (B) = n (A — B)
En sus propias palabras, explique cómo usar la definición de resta. ¿Cuáles son los pasos involucrados?
Ejemplos de cómo hacer restas usando la Definición de Teoría de Conjuntos:
Utilice la definición de la teoría de conjuntos de resta para mostrar que 5 — 2 = 3.
Sea A = {v, w, x, y, z} y B = {w, z}. Dado que n (A) = 5, n (B) = 2 y B\(\subseteq\) A,
\[\begin{aligned} 5 – 2 &= n(A) – n(B) && \text{ by substituting } n(A) \text{ for 5 and } n(B) \text{ for 2} \\ &= n(A – B) && \text{ by the set theory definition of subtraction} \\ &= n(\{v,x,y\}) && \text{ by computing }A – B \\ &= 3 && \text{ by counting the elements in } A – B \end{aligned} \nonumber \]
Por lo tanto, 5 — 2 = 3.
Utilice la definición de la teoría de conjuntos de resta para mostrar que 6 — 1 = 5.
Dejar A {1, 2, 3, 4, 5, 6} y B = {4}. Dado que n (A) = 6, n (B) = 1 y B\(\subseteq\) A,
\[\begin{aligned} 6 – 1 &= n(A) – n(B) && \text{ by substituting } n(A) \text{ for 6 and } n(B) \text{ for 1} \\ &= n(A – B) && \text{ by the set theory definition of subtraction} \\ &= n(\{1, 2, \mathbf{3}, 5, 6\}) && \text{ by computing }A – B \\ &= 5 && \text{ by counting the elements in } A – B \end{aligned} \nonumber \]
Por lo tanto, 6— 1 = 5.
Utilice la definición de la teoría de conjuntos de resta para mostrar que 3 — 0 = 3.
Sea A = {x, y, z} y B= {}. Dado que n (A) =3, n (B) =0 y B\(\subseteq\) A,
\[\begin{aligned} 3 – 0 &= n(A) – n(B) && \text{ by substituting } n(A) \text{ for 3 and } n(B) \text{ for 0} \\ &= n(A – B) && \text{ by the set theory definition of subtraction} \\ &= n(\{x,y,z\}) && \text{ by computing }A – B \\ &= 3 && \text{ by counting the elements in } A – B \end{aligned} \nonumber \]
Por lo tanto, 3 — 0 = 3.
Para cada problema de resta a continuación, proporcione dos conjuntos que le permitan usar la definición de resta para encontrar la respuesta. Después, computa la respuesta usando esta definición.
- 7 - 3
- 6 - 0
- 4 - 4
Las partes b y c del Ejercicio 4 ilustran dos propiedades familiares de la resta.
El primer inmueble establece que para cualquier número entero\(m\),\(m – 0 = m\). Usando nuestro conocimiento de Teoría de Conjuntos, elija el primer conjunto A para tener m elementos y luego elija un segundo conjunto B que tenga cero elementos — solo hay un conjunto que puede elegir y ese es el conjunto nulo o vacío, {}. Entonces, A — {} = A. Por lo tanto, es un hecho que m — 0 = 0.
El segundo inmueble establece que para cualquier número entero m, m — m = 0. Esto debe ser cierto porque para cualquier conjunto A, ya sea que tenga m elementos o cualquier otro número de elementos, sabemos por Teoría de Conjuntos que A — A = {}.
Usaremos el enfoque Take-Away para realizar problemas de resta en Egipto ahora.
Te recuerdan los símbolos y sus equivalentes hindu-árabes a continuación:
| | (1) |
 (10) |
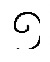 (100) |
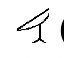 (1,000) |
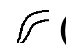 (10,000) |
 (100.000) |
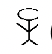 (1,000,000) |
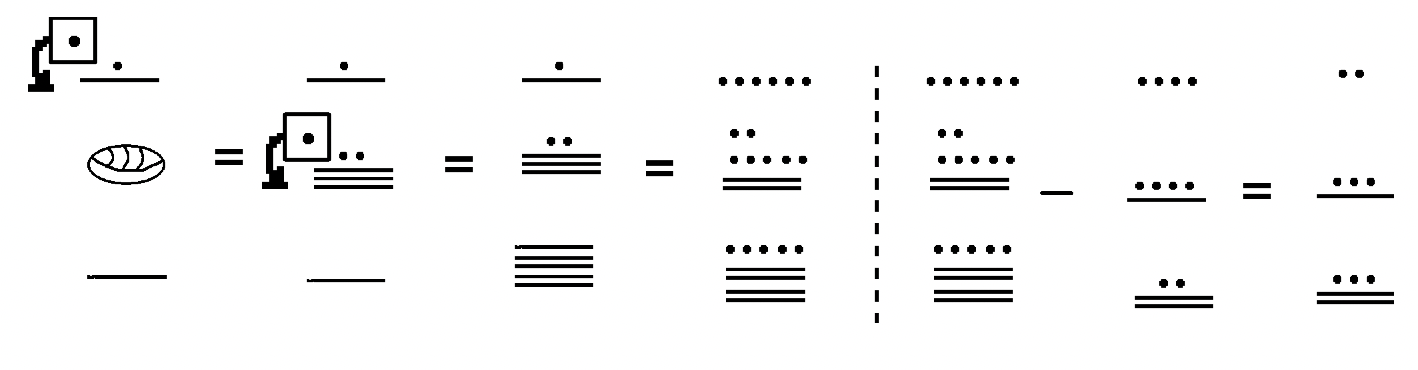
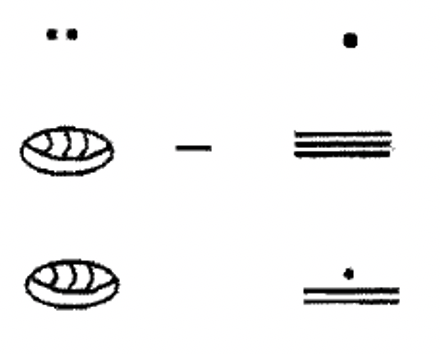
Para usar el enfoque Take-Away, queremos ver el sustraendo como un subconjunto del minuendo y luego eliminar el sustraendo del minuendo. Los símbolos que permanecen en el minuendo es la diferencia. En este primer ejemplo, observe cómo se realiza la siguiente resta. En este caso, se puede ver el sustraendo como un subconjunto del minuendo. Se pone una caja alrededor de lo que se va a llevar y la respuesta final es clara.
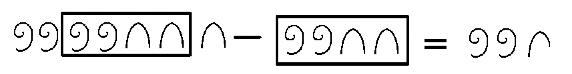
En ocasiones, los intercambios tienen que hacerse en el minuendo antes de que se pueda hacer la resta. Por ejemplo, considere la siguiente resta:
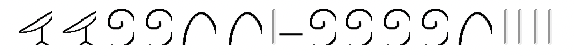
El primer paso sería hacer algunos intercambios en el minuendo. Una flor de loto debe cambiarse por diez pergaminos y un hueso del talón debe cambiarse por diez bastones. Después de hacer eso, la resta se puede realizar como se muestra a continuación:
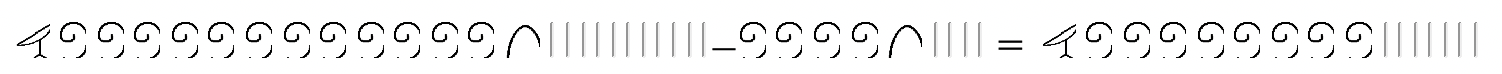
En el ejemplo anterior, ponga una caja alrededor del subconjunto que se está quitando del minuendo.
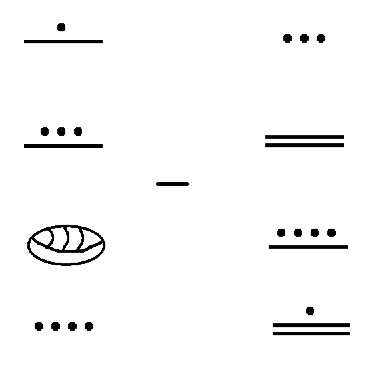
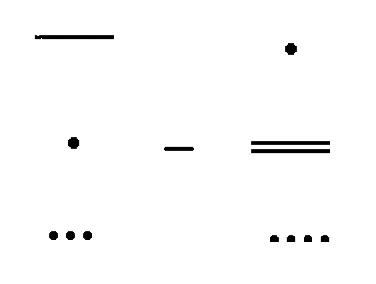
La siguiente resta será
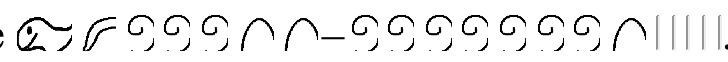
. Esta vez la resta se mostrará como un problema vertical con el minuendo y sustraendo mostrados encerrados en una caja. Para hacer la resta, primero se debe cambiar el dedo puntiagudo en el minuendo por diez flores de loto. Entonces, una flor de loto debe cambiarse por diez pergaminos y un hueso del talón debe cambiarse por diez trazos. Finalmente, el subconjunto (el sustraendo) es quitado del minuendo. He rastreado lo que se está quitando. Los símbolos que quedan en el minuendo es la respuesta (
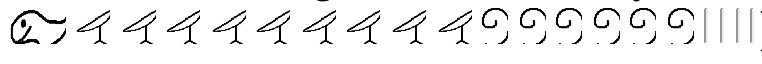
) como se muestra en la siguiente ilustración.
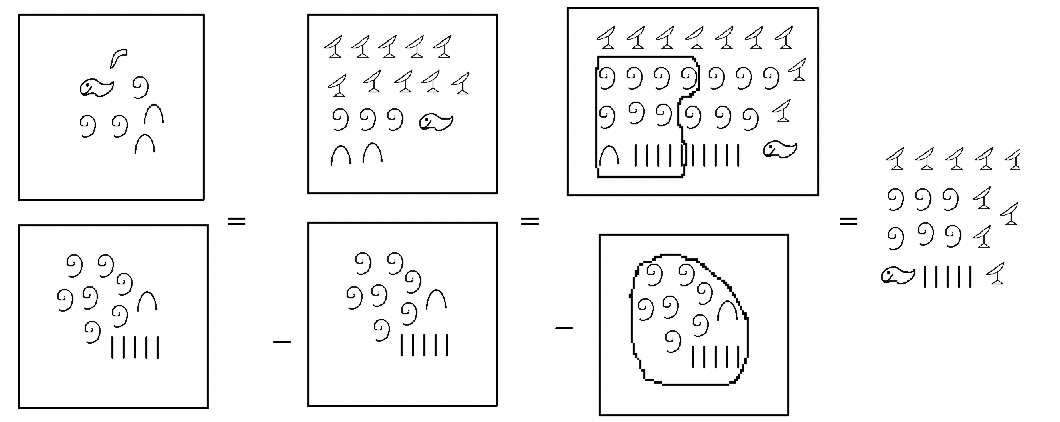
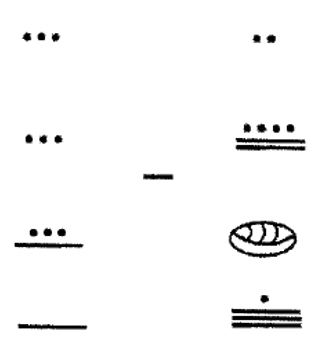
Realiza los siguientes problemas de resta en egipcio, mostrando todos los pasos. Puedes modelar el problema como quieras siempre y cuando los pasos sean claros.
|
a. 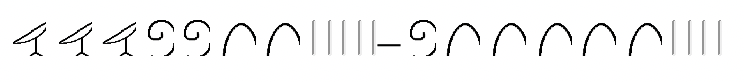 |
b.  |
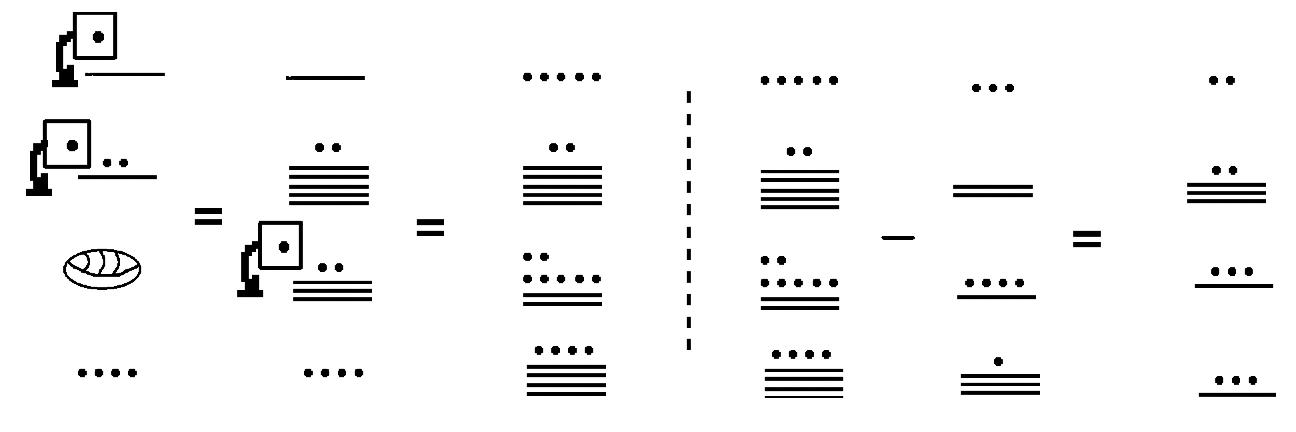
Usemos el enfoque para llevar para restar números mayas. Es similar a la adición en el sentido de que eliminas un subconjunto en cada nivel; es posible que haya que realizar intercambios o operaciones antes de poder quitar en cualquier nivel dado. Presta mucha atención al nivel en el que te encuentras a la hora de hacer intercambios. Un punto en un nivel puede ser negociado por un grupo de 20 en el siguiente nivel abajo excepto del nivel tres al nivel dos — un punto en el tercer nivel es reemplazado por un grupo de 18 en el segundo nivel. Estudia los siguientes ejemplos. A ver si puedes averiguar qué intercambios se están realizando. Indicaré intercambios que se están haciendo de un nivel a otro con una flecha hacia abajo.
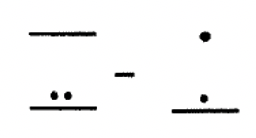
Solución

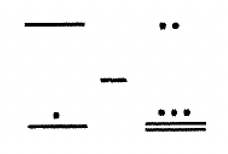
Solución
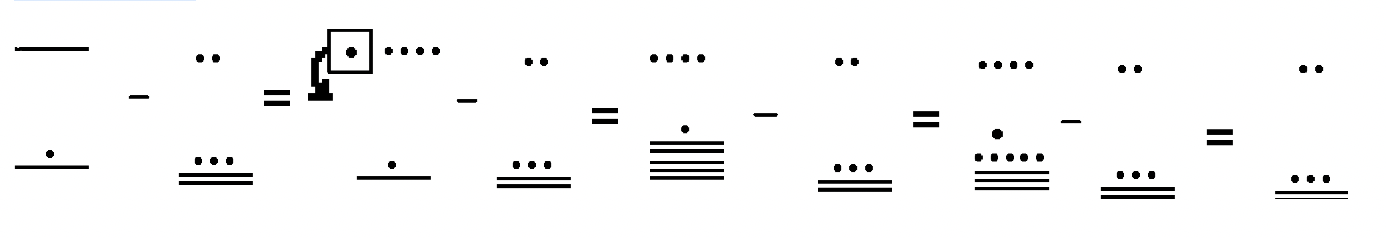
En los Ejemplos 1 y 2, tenga en cuenta que a medida que se están haciendo intercambios en el minuendo (para que pueda usar el enfoque para llevar), el sustraendo simplemente se sigue repitiendo. Como alternativa, primero puedes mostrar los intercambios que se están realizando para el minuendo, hacer una pausa (como una línea punteada como se muestra a continuación) y luego escribir el problema de resta y restar. Aquí hay otra forma, podrías mostrar los pasos para el Ejemplo 2.
Realiza el siguiente problema de resta en maya y muestra todos los pasos.
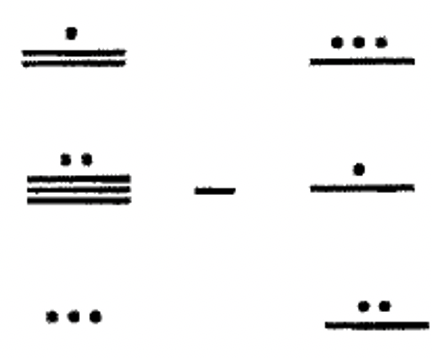
Aquí hay algunos ejemplos más.
Solución
Solución
Se necesita mucha concentración y esfuerzo para trabajar estos correctamente. Realiza cada paso con cuidado porque es fácil cometer errores. Cada uno de los cuatro ejemplos anteriores se puede verificar sumando la respuesta al sustraendo y viendo si la suma es el minuendo. La otra forma de verificar es convertir el minuend y restar al hindu-árabe, restar en hindu-árabe, luego convertir la diferencia a maya, asegurándose de que la respuesta sea la misma que la que se te ocurrió cuando la hiciste en maya. Aquí está la comprobación para el Ejemplo 4:46,084 —25,396 = 20,688. Cometí errores en este problema la primera vez a través, pero encontré mis errores revisando y comenzando de nuevo. Definitivamente deberías revisar tus respuestas. Intenta hacer los ejemplos 3 y 4 anteriores por tu cuenta antes de pasar al siguiente ejercicio.
Realizar los siguientes problemas de resta en maya. Mostrar todos los pasos y comprobar!
 |
 |
 |
 |
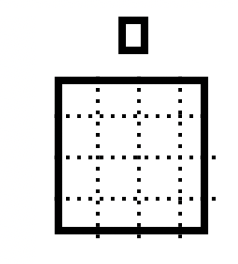
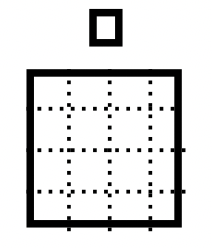
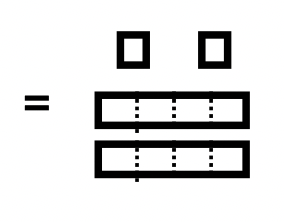
Saca un juego de bloques Base Cuatro. Vamos a hacer el problema de la resta 17 — 7 en Base Cuatro. \(101_{\text{four}}\)es el número Base Cuatro para 17 y\(13_{\text{four}}\) es el número Base Cuatro para 7. Haremos una pila, llamada Pila A, usando los bloques Base Cuatro para representar 17 y otra pila, llamada Pila B, para representar 7. Tus pilas deberían parecerse a lo que ves a la derecha.
 |
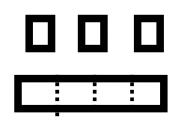 |
A continuación se muestra una ilustración del problema de resta que se está realizando. Para usar el enfoque para llevar, el Pila B debe ser un subconjunto de la Pila A. Ese subconjunto exacto debe eliminarse de la Pila A. Primero, el piso en la Pila A debe cambiarse por 3 largos y 4 unidades para que puedas ver realmente la Pila B dentro de la Pila A. Hay una caja alrededor del subconjunto (Pila B) para ser removida de la Pila A nota cómo coincide con Pila B. Después de quitarle esas cuadras, quedan 2 largos y 2 unidades. Por lo tanto, el problema de resta completado es\(101_{\text{four}} – 13_{\text{four}} = 22_{\text{four}}\).
 Pila A Pila A |
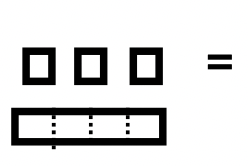 Pila B Pila B |
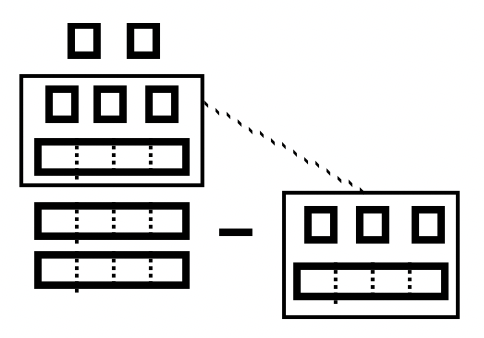 Pila A - Pila B Pila A - Pila B |
 |
¡Sal y usa tus bloques base para hacer los siguientes ejercicios! Siga las indicaciones.
Cuenta 17 bloques unitarios y realiza intercambios con base de cinco bloques. Ponlos en una pila, llamada Pila A, y GUARDA ESTA PILA. Ya que has realizado intercambios en base cinco, escribe 17 como un numeral base cinco en el espacio proporcionado para la Pila A a continuación. Ahora, cuente 9 unidades más y realice intercambios con bloques base cinco. Ponlos en una pila, llamada Pila B. Ya que has realizado intercambios en la base cinco, escribe 9 como un numeral base cinco en el espacio provisto para la Pila B a continuación. Si es necesario, realiza intercambios dentro de la Pila A para que se vea un subconjunto exacto de la Pila B en la Pila A. Quita esos bloques en la Pila A que representan los bloques de la Pila B. Los bloques que quedan en la Pila A son los que quedan después de restar los bloques que estaban en la Pila B. Si es necesario, realiza algún intercambio con base cinco bloques y luego escribir este número como un numeral base cinco en la tercera pieza en blanco que se proporciona a continuación.
A continuación se muestra el problema de resta que acaba de realizar en Base Cinco:
____________ + _____________ = _____________________
Pila A Pila B Diferencia de la pila A y B
Convertir la diferencia (respuesta) a Base Diez. Debería ser 8 ya que 17 — 9 = 8. ¿Lo es?
Ilustrar el problema de la resta usando los bloques a continuación. Mostrar los pasos.
Cuenta 17 bloques unitarios y realiza intercambios con ocho bloques base. Ponlos en una pila, llamada Pila A, y GUARDA ESTA PILA. Ya que has realizado intercambios en base ocho, escribe 17 como un número base ocho en el espacio proporcionado para la Pila A a continuación. Ahora, cuente 7 unidades más y realice intercambios con bloques base ocho. Póngalos en una pila, llamada Pila B. Ya que has realizado intercambios en base ocho, escribe 7 como un numeral base ocho en el espacio provisto para el Pila B a continuación. Si es necesario, realiza intercambios dentro de la Pila A para que se vea un subconjunto exacto de la Pila B en la Pila A. Quita esos bloques en la Pila A que representan los bloques de la Pila B. Los bloques que quedan en la Pila A son los que quedan después de restar los bloques que estaban en la Pila B. Si es necesario, realiza algún intercambio con base ocho bloques y luego escribir este número como un número ocho base en la tercera pieza en blanco que se proporciona a continuación.
A continuación se muestra el problema de resta que acaba de realizar en Base Ocho:
____________ + _____________ = _____________________
Pila A Pila B Diferencia de la pila A y B
Convertir la diferencia (respuesta) a Base Diez. Debería ser 10 desde 17 — 7 = 10. ¿Lo es? Ilustrar el problema de la resta usando los bloques a continuación. Mostrar los pasos.
Cuenta 21 bloques unitarios y realiza intercambios con base de tres bloques. Ponlos en una pila, llamada Pila A, y GUARDA ESTA PILA. Ya que has realizado intercambios en la base tres, escribe 21 como un número base tres en el espacio proporcionado para la Pila A a continuación. Ahora, cuente 7 unidades más y realice intercambios con base de tres bloques. Póngalos en una pila, llamada Pila B. Ya que has realizado intercambios en la base tres, escribe 7 como un numeral base tres en el espacio provisto para la Pila B a continuación. Si es necesario, realiza intercambios dentro de la Pila A para que se vea un subconjunto exacto de la Pila B en la Pila A. Quita esos bloques en la Pila A que representan los bloques de la Pila B. Los bloques que quedan en la Pila A son los que quedan después de restar los bloques que estaban en la Pila B. Si es necesario, realiza algún intercambio con base tres bloques y luego escribir este número como un número base tres en la tercera pieza en blanco que se proporciona a continuación.
A continuación se muestra el problema de resta que acaba de realizar en la Base Tres:
Pila A Pila B Diferencia de la pila A y B
Convertir la diferencia (respuesta) a Base Diez. Debe ser 14 ya que 21 —7 = 14. ¿Lo es? Ilustrar el problema de la resta usando los bloques a continuación. Mostrar los pasos.
Escribe los tres problemas de resta de los ejercicios 8, 9 y 10 en un formato vertical como el de Base Cuatro (mi ejemplo) que se muestra a la derecha. Estudia este problema de Base Cuatro así como los tres problemas que anotas. Trate de encontrar una manera de hacer los problemas de resta usando papel y lápiz en lugar de usar los Bloques Base. En otras palabras, trata de idear tu propio algoritmo (método) para hacer resta en otras bases. Explica tu método y muestra algunos ejemplos. Posteriormente, estarás aprendiendo algoritmos para la resta.
\[ \begin{aligned} 101_{\text{ four}} \\ \underline{ - 13_{\text{ four}}} \\ 22_{\text{ four}} \end{aligned} \nonumber \]
Usando tus Tiras en C, haz dos trenes como se indica. Que B + N sea el primer tren,\(t_{1}\), y que H + R sea el segundo tren,\(t_{2}\). Colocar\(t_{1}\) adyacente a t 2 como se muestra a continuación. Encuentra un tren (escríbalo como una sola tira en C) que, cuando se agrega a t 2, formará un tren de igual longitud a\(t_{1}\). A este tren se le llama la diferencia de los dos trenes,\(t_{1}\)\(t_{2}\) y y se denota por\(t_{1} –t_{2}\). ¿Qué es\(t_{1} –t_{2}\)?

Use Tiras en C para encontrar las siguientes diferencias. Dibuja un diagrama de tu obra.
| a. H — L | b. S — D | c. B — W |
| d. (B + K) — N | e. (O + Y) — P |
Utilice las tiras C para verificar e ilustrar cada una de las siguientes declaraciones:
| a. (S + Y) — Y = S | b. (H — P) + P = H | c. (B + R) — B = R |
| d. H — (L + D) = H — L —D | e. (B + Y) — (K + L) = (B — K) + (Y — L) |
En el Ejercicio 12 se utilizó un nuevo enfoque para definir la diferencia. Hay dos formas distintas de definir la resta: el enfoque para llevar y el enfoque de adición faltante. Podemos usar el modelo de cómo se definió la diferencia usando trenes y ahora aplicarlo a la definición de resta para números enteros. A continuación se muestra una definición de resta usando el modelo de cómo se definió la diferencia usando trenes en el Ejercicio 12.
Definición de resta (enfoque de adición faltante): Que a y b sean dos números enteros cualesquiera. a — b es el número entero c tal que a = b + c. Es decir, si se suma c al sustraendo, b, la suma es el minuendo, a. A la respuesta, c, se le llama la adición faltante.
¿Hay una respuesta de número entero para cada problema de resta de números enteros? En otras palabras, ¿se cierra la resta de números enteros? Explique su respuesta y proporcione un contraejemplo si no está cerrado
Determinar qué conjuntos, si los hay, están cerrados bajo resta. Proporcione un contraejemplo si un conjunto no está cerrado.
| a. {0} | b. {0, 2, 4, 6,...} |
Si piensas en la resta en términos del enfoque de addend faltante, entonces decimos que las declaraciones a — b = c y a = b + c son equivalentes entre sí. Considera la declaración, 8 — 2 = 6. Es equivalente al enunciado 8 = 2 + 6. También sabemos que 2 + 6 = 6 + 2 por la propiedad conmutativa de adición. Por lo tanto, 8 = 6 + 2, que a su vez equivale al enunciado 8 — 6 = 2. Esto nos da cuatro datos sobre cómo relacionar los números 2, 6 y 8 usando suma y resta
| 8 — 2 = 6 |
| 8 = 2 + 6 |
| 8 — 6 = 2 |
| 8 = 6 + 2 |
Algunos maestros relacionan la resta y la suma utilizando la idea de “familias de hechos” como los cuatro hechos anteriores, que es una familia de hecho.
Es importante señalar que cada declaración de suma nos da dos declaraciones de resta, que es la cantidad de personas que aprenden sus hechos de resta. Debido a esta relación entre suma y resta, una vez que un niño aprende hechos básicos de suma, los hechos de resta siguen naturalmente.
Anote dos sentencias de resta que sean equivalentes a cada instrucción de suma.
Quizás se pregunte por qué escribí las declaraciones de adición en el Ejercicio 14 con el signo más a la izquierda del signo igual, a diferencia de la forma en que me pasó a escribir los dos hechos de adición en el hecho familiar que relaciona 2, 6 y 8 en la parte superior de la página. Es porque 8 + 4 = 12 es el mismo hecho que 12 = 8 + 4 debido a la Propiedad Simétrica de Igualdad que se define a continuación.
La Propiedad Simétrica de Igualdad establece que para cualquier ecuación, si a = b, entonces también es cierto que b = a
Por lo tanto, está perfectamente bien escribir los cuatro hechos anteriores como
| 2 + 6 = 8 |
| 6 + 2 = 8 |
| 8 — 2 = 6 |
| 8 — 6 = 2 |
Utilice la propiedad simétrica de igualdad para reescribir cada ecuación.
| a. 7 — 3 = 4: _____ | b. 9 — 1 = 8: _____ |
¿Existe una propiedad simétrica de la desigualdad? Explique.
Nota: La desigualdad se refiere a menos de (<) and/or greater than (>).
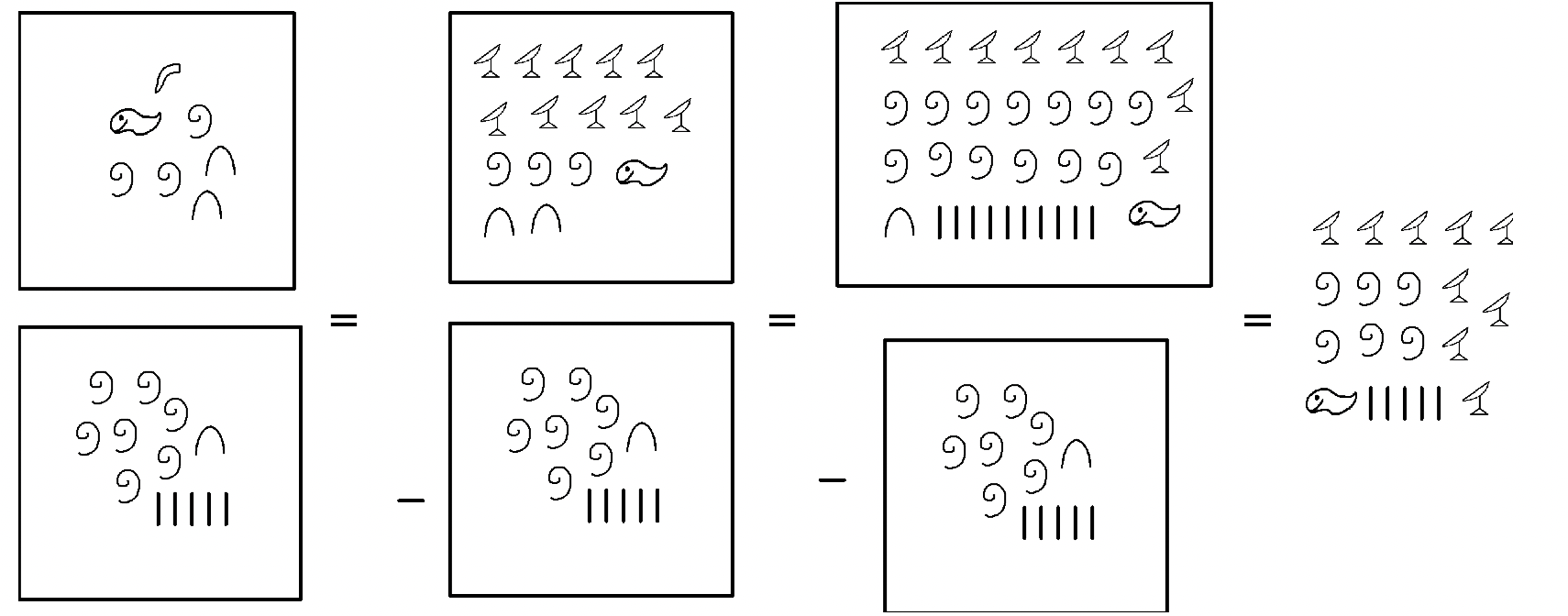
Hagamos un problema de resta usando el enfoque de addend faltante en egipcio. La configuración es exactamente la misma que cuando se emplea el enfoque para llevar, pero la forma en que vas a encontrar la respuesta es diferente. El primer ejemplo que vimos en egipcio fue
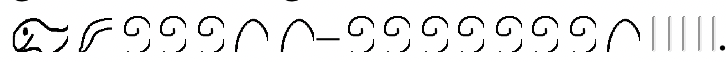
Nos preguntamos “Qué hay que sumar a
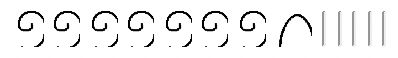
para obtener
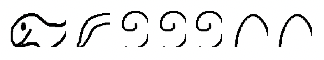
?” Otra forma de expresarlo es escribir:
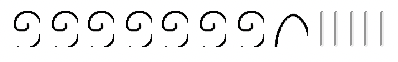
+????? =
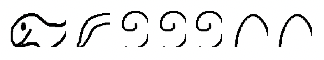
. Comenzamos por convertir en el minuendo hasta que contenga el sustraendo. Hicimos estos pasos exactos al usar el enfoque para llevar. Pero para obtener la respuesta final, notamos lo que hay que sumar al sustraendo para obtener el minuendo. La respuesta es

. La ilustración se muestra a continuación.
Para verificar, ver si el adenda faltante (la respuesta) + el sustraendo = el minuendo. En otras palabras, ¿es cierta la siguiente declaración de adición?
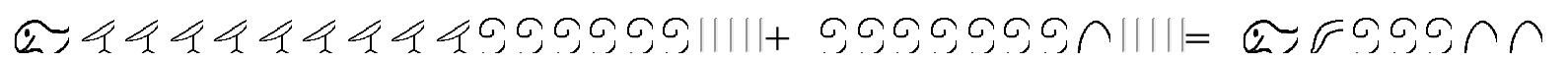
Otra forma de verificar es convertir al hindu-árabe.
El mismo enfoque podría ser utilizado para restar en maya. Los pasos utilizados para prepararse para encontrar el adenda faltante son exactamente los mismos que cuando se emplea el enfoque para llevar. Pero para calcular la respuesta, en cada nivel decides qué símbolos se deben sumar al sustraendo para obtener lo que hay en el minuendo.
Aunque puede ser difícil distinguir entre los dos enfoques de la resta, es la forma en que piensas sobre el problema lo que lo hace diferente. Por ejemplo, un niño aprendiendo sobre la resta podría pensar en el problema 8 — 3 al pensar “Si tengo 8 centavos en una mano y me llevo 3 de ellos para poner en mi bolsillo, ¿cuántos quedan en mi mano?” Este es el enfoque para llevar. El niño podría calcular la respuesta contando hacia atrás —7, 6, 5 o usando realmente centavos o manipuladores donde se ponen 8 centavos en una mano, se quitan 3 y lo que queda se cuenta para obtener la respuesta. Otro niño podría pensar en el mismo problema de resta de esta manera —"Si tengo 3 centavos, ¿cuántos peniques más necesito para que tenga 8 centavos?” Este es el enfoque de adenda que falta.
Conformar dos problemas de palabras que requerirían que se calculara el problema de resta 8 — 3. El primero debe usar el enfoque para llevar y el segundo debe usar el enfoque de adición faltante. Explica y muestra cómo resolverías cada problema de palabras usando el enfoque dado.
| a. Enfoque para llevar |
| b. Enfoque de adición faltante |
Sin usar manipulativos, cada problema de resta se puede redactar como un problema de adición faltante. En otras palabras, para encontrar la respuesta a 8 — 3, averiguas qué va en el espacio en blanco para 3 + ____ = 8. Desde 3 + 5 = 8, luego 8 — 3 = 5.
Realice los siguientes problemas de resta empleando el enfoque de addend faltante. Rellenar los espacios en blanco
| a. 9 — 7 = ____ porque _____________ |
| b. 13 — 6 = ____ porque _____________ |
| c. 88 — 8 = ____ porque ______________ |
| d. 70 — 14 = ____ porque _____________ |
Utilice Bloques Base para calcular los siguientes problemas de resta usando el enfoque de adición faltante. Comienza formando dos pilotes, uno para el minuendo (Pila A) y otro para el sustraendo (Pila B). Entonces averigua qué debe ir en una tercera pila (Pila X) para que B + X = A. Muestra cómo encontraste la respuesta.
\(231_{\text{five}} – 140_{\text{five}}\)
\(100_{\text{two}} – 11_{\text{two}}\)
\(135_{\text{twelve}} – T6_{\text{twelve}}\)
El enfoque de adición faltante a veces se llama Algoritmo Aditivo (o Austriaco).
Este enfoque es muy útil para hacer sustracción en la recta numérica.
Revisemos la definición de resta utilizando el enfoque de addend faltante. Dice la respuesta a a — b = c donde c es el número que se debe sumar a b para obtener c, o b + c = a.
Piense en esto usando una línea numérica. ¿Cómo encontraríamos la respuesta a 7 — 3? Necesitamos encontrar un número para sumar al 3 que nos dé una respuesta de 7. Es decir, ¿qué iría en el espacio en blanco 3 + ____ = 7? Sé que conoces la respuesta, pero ¿cómo podríamos obtener la respuesta usando una línea numérica?
Primero, tenemos que definir un nuevo término: vector. Un vector es un segmento de línea dirigido. Básicamente, un vector dirigido parece una flecha. Tiene cierta longitud y apunta en cierta dirección. Ya que usaremos líneas numéricas horizontales, usaremos vectores horizontales. Una flecha que apunte a la derecha denotará un número positivo y una flecha que apunte a la izquierda denotará un número negativo.
A continuación se muestra una línea numérica, con algunos vectores mostrados arriba. El vector a tiene 6 unidades de largo y la flecha apunta a la derecha. Por lo tanto, representa el número +6. El vector b también tiene 6 unidades de largo, pero apunta a la izquierda. Por lo tanto, representa el número -6.

a. ¿Qué número representa el vector c? _________
b. ¿Qué número representa el vector d? _________
Ahora, estamos listos para usar vectores junto con el enfoque de addend faltante para calcular un problema de resta. Volvamos al problema 7 — 3. El enfoque de addend faltante establece que la respuesta al problema de resta es el número que cuando se suma al número después del signo de resta da el número que está antes del signo de resta. Ya que 3 es el número después del signo de resta, tenemos que encontrar un número para sumar a 3 que dará una respuesta de 7. Usando una línea numérica, esto significa que si comienzas en 3, ¿cómo puedes llegar al 7? En otras palabras, dibuja un vector que comience en 3 y termine en 7. Asegúrate de que la flecha apunte a 7. El número que representa el vector es la respuesta al problema. La ilustración se muestra a continuación. El vector tiene longitud 4 y apunta a la derecha, por lo que la respuesta es 4, que se escribe encima del vector para indicar la respuesta.

Probemos el problema 2 - 9. Entonces, 9 + ____ = 2. En la recta numérica, dibuje un vector que comience en 9 y termine en 2. Entonces, vea qué número representa el vector para encontrar la respuesta. El vector que se muestra a continuación da la respuesta de -7.
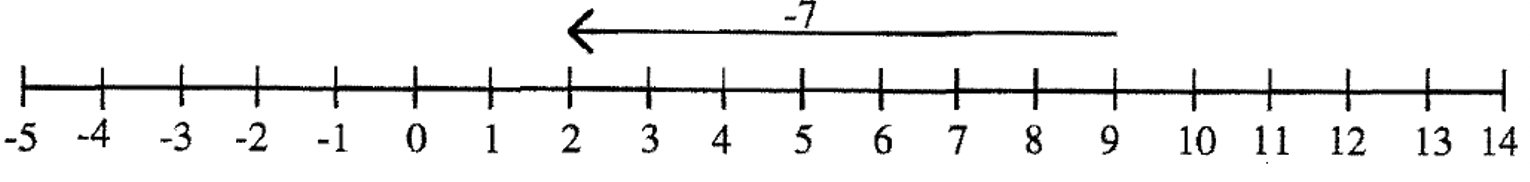
Encuentre la respuesta a los siguientes problemas de resta usando vectores dirigidos en la línea numérica junto con el enfoque de adición faltante. Dibuja los vectores.
|
a. 10 - 4 =  |
|
b. 12 - 5 =  |
|
c. 8 - 3 =  |
|
d. 9 - 7 =  |
|
e. 3 - 10 =  |
|
f. 5 - 8 =  |
|
g. 1 - 13 =  |
|
h. 9 - 9 =  |
Al observar los vectores a — d a continuación, averigüe qué problema de resta se estaba realizando, y luego indique la respuesta. Por ejemplo, el vector b vino de hacer el problema -1 — 5. Entonces, -1 — 5 = -6 (ya que el vector b tiene 6 unidades de largo y va a la izquierda).

| Vector a: ____ | Vector b: ____ | Vector c: ____ |


