6.1: Suma y resta
- Page ID
- 113361
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Necesitarás: Contadores Positivos y Negativos (Tarjetas de Material 18A y 18B)
Recuerda que los números enteros están conformados por cero y los números de conteo: 0, 1, 2, 3, 4, 5,. Cuando los escolares ven por primera vez una línea numérica, generalmente se enfocan en los números enteros y la recta numérica se ve así:
En este modelo, la recta numérica comienza en cero, y la flecha a la derecha indica que continúa indefinidamente hacia la derecha. En realidad, hay infinitamente muchos números (o puntos) entre dos números cualesquiera en la recta numérica. Por ejemplo, algunos del número infinito de puntos entre 1 y 2 son 3/2, 4/3, 5/4, 6/5, 7/5, 8/5, etc. En la recta numérica, también hay infinitamente muchos números irracionales. Los números irracionales no pueden escribirse como la proporción de dos números enteros, como la forma en que representamos fracciones reducidas. Ejemplos de algunos números irracionales entre 3 y 4 son\(\sqrt{11}\),\(\sqrt{15}\), 3.10110111..., y\(\pi\). Contrario a la creencia popular,\(\pi\) no equivale a 3.14 y\(\pi\). no equivale a 22/7. Tanto 3.14 como 22/7 son números racionales (a diferencia de\(\pi\) lo que es un número irracional, NO un número racional) y 3.14 y 22/7 son solo aproximaciones comúnmente utilizadas al calcular con\(\pi\). Los números irracionales serán explorados y discutidos con más detalle en un módulo diferente.
Bien, volvamos a nuestra discusión de la línea numérica. La línea numérica que se muestra al comienzo de este conjunto de ejercicios es realmente solo una media línea, por lo que llamarlo una línea numérica es realmente un nombre inapropiado. Una línea horizontal continúa indefinidamente tanto en dirección izquierda como derecha, no solo hacia la derecha. Los números a la derecha de cero se denominan números positivos. Los números a la izquierda de cero se denominan números negativos. Cero es el único número que no tiene signo —no es ni positivo, ni negativo. Para cada número positivo, hay un número negativo correspondiente, que en una línea numérica dada, está a la misma distancia de cero que el número positivo, pero está al lado izquierdo del cero. Los números a la misma distancia de pero en lados opuestos de cero se llaman “opuestos”. Los números negativos se representan así: -5 se lee “cinco negativos”, -20 se lee “veinte negativos”, etc. Entonces, 5 y -5 son opuestos, 20 y -20 son opuestos, y cero es lo opuesto de sí mismo.
Para cada marca en la línea numérica, rellene los números que faltan
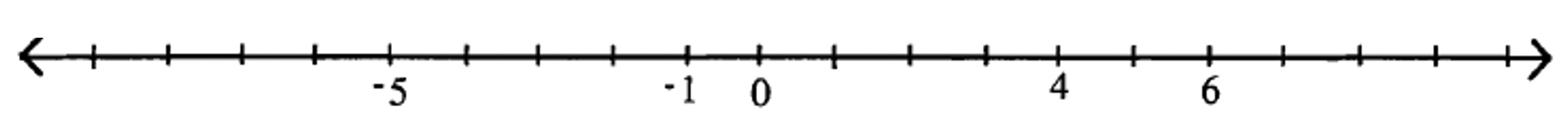
Definiciones: El conjunto de enteros positivos (que también se denominan comúnmente los números naturales o números de conteo) se escribe como: {1, 2, 3, 4,...}. Los números positivos también se pueden escribir con un signo positivo antes de él. Por ejemplo, 4 puede escribirse un +4.
El conjunto de números enteros contiene tanto cero como los números naturales y se escribe como: {0, 1, 2, 3,...}.
Definición: El conjunto de enteros negativos contiene exactamente todos los opuestos de todos los enteros positivos.
1. Escribe el conjunto de enteros negativos:
Definición: El conjunto de enteros se compone de cero, los enteros positivos y los enteros negativos.
2. Escribe el conjunto de enteros:
Definición: El valor absoluto de un número en la recta numérica se define como la distancia que ese punto es desde cero. Dado que el valor absoluto se define en términos de distancia, nunca puede ser negativo. Para evaluar el valor absoluto de un número, indicar la distancia que es desde cero.
El valor absoluto de 5 es 5, ya que la distancia de 5 a 0 es de 5 unidades. El valor absoluto de -5 también es 5, ya que la distancia de -5 a 0 también es de 5 unidades.
Evaluar el valor absoluto de cada uno de los siguientes números:
| a. 4: ____ | b. -8: ____ | c. 2: ____ | d. -1: ____ | e. 0: ____ |
Para indicar el valor absoluto de un número, lo encerramos entre dos líneas verticales. “El valor absoluto de -15 es 15" se escribe así: | -15 | = 15. Para simplificar un problema con un signo de valor absoluto, primero se debe simplificar la parte dentro del signo de valor absoluto. Entonces, si la parte dentro del signo de valor absoluto no es simplemente un numeral, piense en la parte interior como entre paréntesis, y simplifíquela primero. Entonces, toma el valor absoluto del numeral. Tendrás que hacer esto para las partes c y f del ejercicio 4.
Simplifica cada uno de los siguientes:
| a. | 7 | = ______ | c. | 7 — 3 | = _______ | |
| d.\(|\frac{3}{7}|\) = ______ | e.\(|-\frac{3}{7}|\) = ______ | f. | 2\(\cdot\) 5 — 4 | = _______ |
Escribe dos números que tengan un valor absoluto de 6 ______ y _______
Escribe dos números que tengan un valor absoluto de 19 ______ y ______
Escribe todos los números que tengan un valor absoluto de cero _______
Escribe todos los números que tengan un valor absoluto de -10 (negativo 10) _______
Cada número positivo y negativo se puede representar con un segmento de línea dirigido llamado vector.
Básicamente, un vector parece una flecha. Tiene dos propiedades: tiene una cierta longitud (llamada la “magnitud”) y apunta en cierta dirección. Como vamos a estar usando líneas numéricos horizontales, vamos a estar dibujando vectores horizontales. Una flecha que apunte a la derecha denotará un número positivo y una flecha que apunte a la izquierda denotará un número negativo.
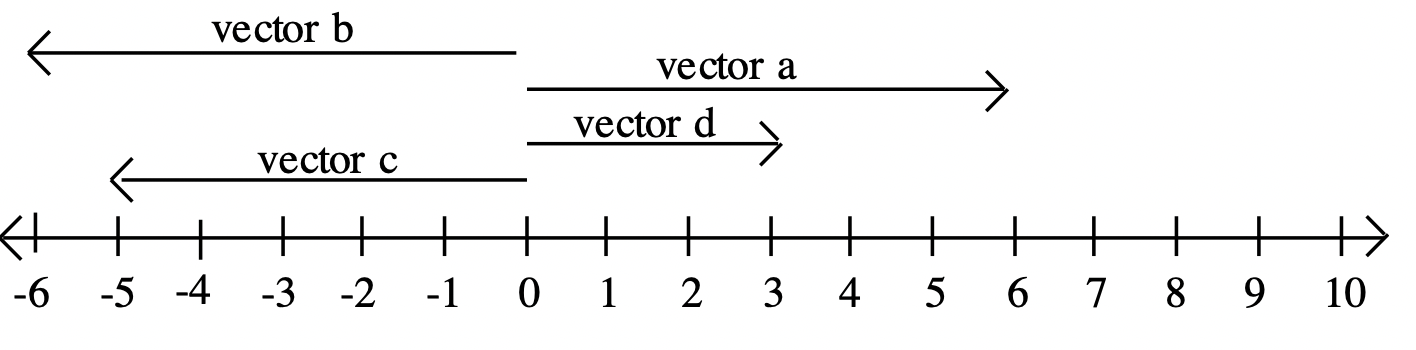
A continuación se muestra una línea numérica, con algunos vectores mostrados arriba. El vector a tiene 6 unidades de largo y la flecha apunta a la derecha. Por lo tanto, representa el número +6. El vector b también tiene 6 unidades de largo, pero apunta a la izquierda. Por lo tanto, representa el número -6. Ambos vectores tienen una magnitud de 6.

- ¿Qué número representa el vector c? _________
- ¿Qué número representa el vector d? _________
Cada vector tiene un punto inicial (el punto inicial del vector) y un punto terminal (el punto final, donde se muestra la flecha). Si el punto inicial del vector se coloca en cero, la línea numérica se puede usar como un marcador conveniente: el punto terminal del vector simplemente se coloca en el número que se representa. Pero no es necesario representarlo de esa manera, como se pudo ver en todos los vectores mostrados en los ejemplos anteriores. Los vectores a, b, c y d podrían haberse dibujado con el punto inicial en cero como se muestra a continuación. Si dibujas un vector con su punto inicial en cero, el número que representa el vector es simplemente el mismo número en la línea numérica donde aterriza su punto terminal.
Otra forma de pensar sobre los números es pensar en ellos en términos de "acciones”. Se podría pensar en el número “5" como la acción de mover 5 espacios hacia la derecha. Cuando dibujas el vector que representa 5, esa es una manera de mostrar esa acción en particular. Se podría pensar en el número “-3" como la acción de mover 3 espacios hacia la izquierda. Cuando dibujas el vector que representa -3, esa es una manera de mostrar esa acción en particular.
La recta numérica, junto con esta idea de pensar en los números en términos de acciones, se puede utilizar para sumar números juntos.
Definición: Para sumar dos números, m y n, HACES la primera acción, m. El signo de suma significa AHORA HACER la segunda acción, n. La respuesta al problema (que es la suma: m + n) es la acción única que podría haberse hecho para lograr el mismo resultado que hacer las acciones separadas en sucesión.
Considera esta forma práctica de pensarlo. Piense en caminar hacia el este como representar un número positivo y caminar hacia el oeste como representar un número negativo. Si caminabas 5 cuadras al este, luego 7 cuadras al oeste, luego 3 cuadras al este, estarías una cuadra al este de tu punto de partida original. Esta puede ser una forma de pensar sobre el problema: 5 + (-7) + 3 = 1.
- Escoja un punto de partida y dibuje el vector m (que es una forma de representar la acción de m) con su punto inicial en el punto de partida designado.
- El signo de suma significa comenzar en el punto terminal de la acción anterior HACER la siguiente acción. Entonces, dibuja el vector n, colocando el punto inicial de n en el punto terminal del vector m.
- La suma, m + n, es el mismo número que estaría representado por un vector con su punto inicial colocado en el punto de partida original y su punto terminal en el punto terminal final después de que tuvo lugar la última acción.
Solo por CONVENIENCIA, es más fácil usar siempre una línea numérica y elegir cero como punto de partida inicial. Al hacer eso, la respuesta al problema será donde sea que el punto terminal de la última acción aterrice en la recta numérica.
Antes de continuar, es importante señalar que no es necesario marcar cada punto en una recta numérica. De hecho, esto es imposible ya que hay infinitamente muchos puntos en una recta numérica. No obstante, suele ser una buena idea marcar cero y al menos un punto a cada lado de cero. Marque la línea numérica de una manera que sea conveniente para hacer el problema.
Usaremos el procedimiento anterior para agregar los siguientes números. Para estos ejemplos y para los ejercicios, comience en cero por conveniencia. Dibuja el primer vector. Después muévete un poco hacia arriba para dibujar el segundo vector por lo que es obvio qué vector se dibujó primero y cuál se dibujó el último. Se debe mostrar un vector por cada número en la suma. Ya que estamos colocando el punto inicial del primer vector en cero, podemos afirmar la respuesta señalando dónde aterrizó el punto terminal del último vector en la línea numérica.
4 + 2.
Solución
Comenzando en cero, HACER la acción 4 (que se muestra dibujando el vector que representa 4), luego comenzando en el punto donde terminó la primera acción, HACER la acción 2 (que se muestra dibujando el vector que representa 2).
La respuesta es 6 ya que el punto terminal del último vector aterrizó en 6.
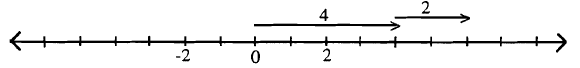
-5 + 3.
Solución
Comenzando en cero, HACER la acción -5 (que se muestra dibujando el vector que representa -5), luego HACER la acción 3 (que se muestra dibujando el vector que representa 3).
La respuesta es -2 ya que el punto terminal del último vector aterrizó en -2.
-3 + -4.
Solución
Comenzando en cero, HACER la acción -3 (se muestra dibujando el vector que representa -3), luego HACER la acción -4 (se muestra dibujando el vector que representa -4).
La respuesta es -7 ya que el punto terminal del último vector aterrizó en -7.
-4 + 8.
Solución
Comenzando en cero, HACER la acción -4 (que se muestra dibujando el vector que representa -4), luego HACER la acción 8 (que se muestra dibujando el vector que representa 8).
La respuesta es 4 ya que el punto terminal del último vector aterrizó en 4.
50 + -35.
Comenzando en cero, HACER la acción 50 (se muestra dibujando el vector que representa 50), luego HACER la acción -35 (mostrada dibujando el vector que representa -35).
La respuesta es 15 ya que el punto terminal del último vector aterrizó en 15.

Es IMPERATIVO que ETIQUES tu línea numérica. De lo contrario, no está claro qué representa cada vector. No asuma que cada marca representa 1 unidad. Sin la etiqueta de al menos un número a cada lado del cero en el último ejemplo, se podría suponer que el último ejemplo mostrado representaba 10 + -7 y que la respuesta era 3.
Utilice vectores en la recta numérica para sumar los siguientes números juntos. Marque y ETIQUE su línea numérica con al menos cero y un punto a cada lado.
Aquí hay un ejemplo de cómo hacer los siguientes problemas:
-4 + 8 + (-5) = -1 ya que el punto terminal del último vector aterrizó en -1.

|
a. 5 + (-8) = _____ desde ______________________________________________  |
|
b. -7 + (-2) = _____ desde _____________________________________________  |
|
c. -5 + 9 = _____ desde _____________________________________________  |
|
d. 7 + (-6) = _____ desde ______________________________________________  |
|
e. -7 + 5 = _____ desde ______________________________________________  |
|
f. -100 + 40 = _____ desde ______________________________________________  |
|
g. -3 + (-2) + 4 = _____ desde ___________________________________________  |
|
h. 4 + (-12) + 5 = _____ desde ______________________________________________  |
A veces, verás líneas numéricos verticales en lugar de líneas numéricos horizontales. En este caso, los números positivos van hacia arriba, y están representados por vectores verticales con la flecha apuntando hacia arriba. Asimismo, los números negativos bajan y están representados por vectores verticales apuntando hacia abajo. A la derecha se muestra un ejemplo de una recta numérica vertical.
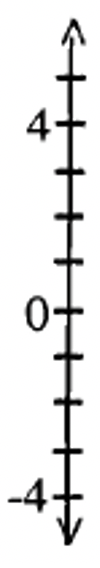
Existe un uso común de usar una línea numérica vertical. ¿Se te ocurre uno? A ver si se le ocurre alguna y anote alguna aquí abajo.
Si necesitas una pista para el Ejercicio 11, piensa en el clima.
Seguiremos pensando en las acciones a medida que usamos vectores para hacer problemas de resta.
Definición: Para restar un número, m, DESHACES la acción, m lo que significa HACER LO OPUESTO de la acción m.
Ya sea que esté o no haciendo un problema de resta, un problema de suma, o ambos en el mismo problema, la respuesta al problema es la acción única que se podría haber hecho para lograr el mismo resultado que hacer las acciones separadas en sucesión.
Se puede pensar en la resta como deshacer algún error.
Considera una variación del ejemplo original dado para la adición. Para refrescar tu memoria, aquí estaba ese problema: Piense en caminar hacia el este como representar un número positivo y caminar hacia el oeste como representar un número negativo. Si caminabas 5 cuadras al este, luego 7 cuadras al oeste, luego 3 cuadras al este, estarías una cuadra al este de tu punto de partida original. Esta puede ser una forma de pensar sobre el problema: 5 + (-7) + 3 = 1.
Imagina que caminaste 5 cuadras al este, luego 2 cuadras al oeste, y luego te diste cuenta de que habías cometido un error No se suponía que caminaras 2 cuadras al oeste. Tendrías que deshacer ese error. ¿Qué harías para deshacer ese error y volver a donde estabas antes de caminar 2 cuadras al oeste en accidente?
En el ejercicio 12, espero que te hayas dado cuenta de que necesitabas caminar 2 cuadras al este para deshacer tu error. Para traducir los pasos dados en #12, podríamos escribir 5 + (-2) — (-2) = 5. Así es como explicaríamos y mostraríamos las acciones usando vectores en la recta numérica.
5 + (-2) — (-2): Comenzando en cero, HACER la acción 5 (mostrada dibujando el vector que representa 5), luego HACER la acción -2 (mostrada dibujando el vector que representa -2), luego DESHACER la acción de -2 (que significa HACER EL OPUESTO de la acción -2, que es HACER la acción +2, mostrada dibujando el vector que representa +2).
La respuesta es 5 ya que el punto terminal del último vector aterrizó en 5.

Procedimiento para usar vectores para sumar o restar dos números:
- Si el primer número es m, elija un punto de partida y dibuje el vector m (que es una forma de representar la acción m) con su punto inicial en el punto de partida designado.
- Si el siguiente signo es suma, HACER la siguiente acción dibujando el vector que representa el siguiente número, colocando el punto inicial de este vector en el punto terminal del vector anterior. Si, por otro lado, el siguiente signo es la resta, DESHACER la siguiente acción. Entonces, dibuja el vector que representa lo opuesto del siguiente número, colocando el punto inicial de este vector en el punto terminal del vector anterior.
- Si hay otra señal de suma o resta, regrese al paso 2. De lo contrario, en este punto, podemos encontrar la respuesta. La respuesta es el mismo número que estaría representado por un vector con su punto inicial colocado en el punto de partida original y su punto terminal en el punto terminal final después de que tuvo lugar la última acción.
Nuevamente, usar cero como punto de partida es CONVENIENTE porque la respuesta al problema será dondequiera que el punto terminal de la última acción aterrice en la recta numérica.
Utilizaremos el procedimiento anterior para calcular los siguientes problemas. Para estos ejemplos y para los ejercicios, comience en cero por conveniencia. Dibuja el primer vector. Después muévete un poco hacia arriba para dibujar el segundo vector por lo que es obvio qué vector se dibujó primero y cuál se dibujó el último. Debe mostrarse un vector por cada número en el problema. Ya que estamos colocando el punto inicial del primer vector en cero, podemos afirmar la respuesta señalando dónde aterrizó el punto terminal del último vector en la línea numérica.
4 — (-2).
Solución
Comenzando en cero, HACER la acción 4 (que se muestra dibujando el vector que representa 4), luego DESHACER la acción -2 (lo que significa HACER EL OPUESTO de la acción -2, que es HACER la acción +2, mostrada dibujando el vector que representa +2).
La respuesta es 6 ya que el punto terminal del último vector aterrizó en 6.
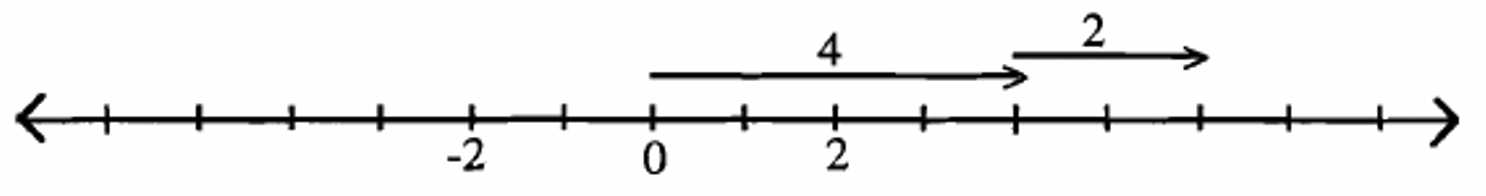
-5 — (-3).
Solución
Comenzando en cero, HACER la acción -5 (mostrada dibujando el vector que representa -5), luego DESHACER la acción -3 (lo que significa HACER el OPUESTO de la acción -3, que es HACER la acción +3, mostrada dibujando el vector que representa +3).
La respuesta es -2 ya que el punto terminal del último vector aterrizó en -2.
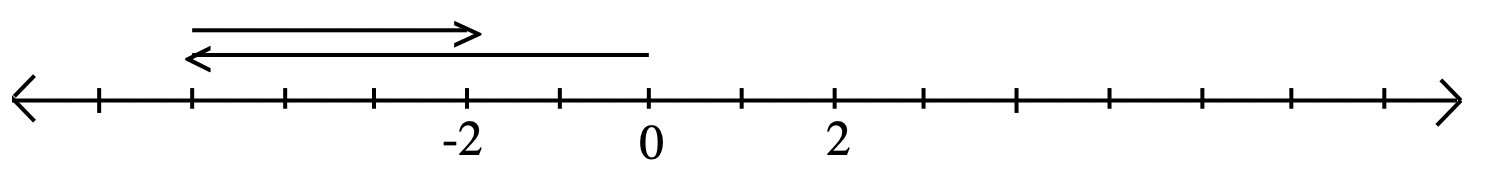
-3 — (+4).
Solución
Comenzando en cero, HACER la acción -3 (que se muestra dibujando el vector que representa -3), luego DESHACER la acción +4 (lo que significa HACER el OPUESTO de la acción +4, que es HACER la acción -4, que se muestra dibujando el vector que representa -4).
La respuesta es -7 ya que el punto terminal del último vector aterrizó en -7.

-4 — (-8).
Solución
Comenzando en cero, HACER la acción -4 (que se muestra dibujando el vector que representa -4), luego DESHACER la acción -8 (lo que significa HACER el OPUESTO de la acción -8, que es HACER la acción +8, mostrada dibujando el vector que representa +8).
La respuesta es 4 ya que el punto terminal del último vector aterrizó en 4.

50 + (-35).
Solución
Comenzando en cero, HACER la acción 50 (se muestra dibujando el vector que representa 50), luego HACER la acción -35 (mostrada dibujando el vector que representa -35).
La respuesta es 15 ya que el punto terminal del último vector aterrizó en 15.
Es IMPERATIVO que ETIQUES tu línea numérica. De lo contrario, no está claro qué representa cada vector. No asuma que cada marca representa 1 unidad. Sin la etiqueta de al menos un número a cada lado del cero en el último ejemplo, se podría suponer que el último ejemplo mostrado representaba 10 + (-7) y que la respuesta era 3.
Utilice vectores en la recta numérica para sumar los siguientes números juntos. Marque y ETIQUE su línea numérica con al menos cero y un punto a cada lado.
Aquí hay un ejemplo de cómo hacer los siguientes problemas:
-4 + 8 + (-5) = -1 ya que el punto terminal del último vector aterrizó en -1.

|
a. 5 — (+8) = _____ desde __________________________________________.  |
|
b. -7 — (+2) = _____ desde __________________________________________.  |
|
c. -5 — (-9) = _____ desde _____________________________________________.  |
|
d. 7 — (+6) = _____ desde __________________________________________.  |
|
e. -7 — (-5) = _____ desde __________________________________________.  |
|
f. -100 — (-40) = _____ desde __________________________________________.  |
|
g. -3 — (+2) — (-4) = _____ desde __________________________________________.  |
|
h. 4 — (+12) + 5 = _____ desde __________________________________________.  |
En este punto, sería beneficioso si volvieras a mirar los ejemplos de las páginas 4 y 5 y compararlos con los ejemplos recientes que se muestran en las páginas 8 y 9. Los ejemplos de las páginas 8 y 9 incluyen la resta, mientras que los ejemplos de las páginas 4 y 5 son problemas de suma. Usando la idea de sumar y restar usando vectores y el enfoque de acción (ya sea DO o DESHACER una acción), los problemas cuando se hace con vectores en la recta numérica se ven exactamente iguales. Lo mismo es cierto si nos fijamos en los problemas en los Ejercicios 10 y 13. De alguna manera, entonces, parece haber una conexión entre la resta y la suma. Lo pondremos todo junto después de explorar una forma muy diferente de sumar y restar, esta vez usando manipuladores.
Otra forma de representar números positivos y negativos es mediante el uso de una colección de contadores positivos y negativos. Es necesario usar contadores de un color para representar números positivos (cada contador = +1) y contadores de otro color para representar números negativos. Si usas las tarjetas de material, cada cuadrado verde representará +1 y cada cuadrado rojo representará -1. Descubriremos que hay muchas formas de representar el mismo número usando estos contadores. Saca tus contadores para hacer los siguientes ejercicios.
La forma más sencilla de representar un número positivo, x, es tener una colección de x contadores verdes. La forma más sencilla de representar un número negativo, -y, es tener una colección de y contadores rojos. Por ejemplo, 4 contadores rojos representarán -4 y 3 contadores verdes representarán +3. En estos ejercicios, a veces representaré un contador positivo ya sea por un cuadrado o círculo con un signo positivo (+) o una “G” en su interior, o simplemente por una “G”. De igual manera, un contador negativo se representará ya sea por un cuadrado o círculo con un signo negativo (-) o una “R” en su interior, o simplemente por una “R”.
¿Qué número representa cada una de las siguientes colecciones?
|
a. 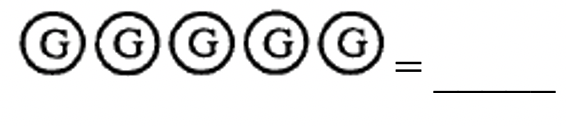 |
b. RRRRRRRRRR = ______ |
|
c. 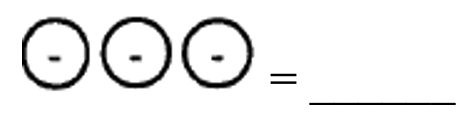 |
d. 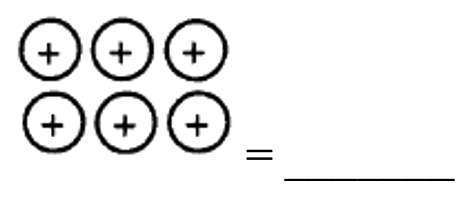 |
Debajo de cada número, representa el número mostrando una colección de contadores.
| b. 2 |
Ejercicio 16
¿Qué número crees que representa la colección a continuación? ______ Explique por qué.
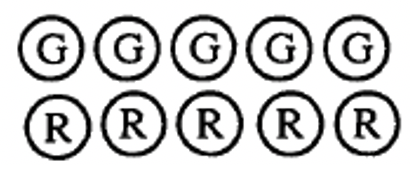
En el ejercicio 14, hubo 5 positivos y 5 negativos. ¿Se te ocurrió una respuesta de cero? Si es así, estás en el camino correcto. Básicamente, cuando un contador positivo se empareja con un contador negativo, se anulan entre sí. Cada vez que hay el mismo número de contadores positivos que los contadores negativos, se tiene una representación del número, cero.
Mediante el uso de contadores positivos y negativos, se muestran tres representaciones diferentes de cero.
| a. | b. | c. |
Veamos si puedes averiguar qué número representa cada colección.
Anotar el número representado por cada colección
|
a. La siguiente colección representa _____ 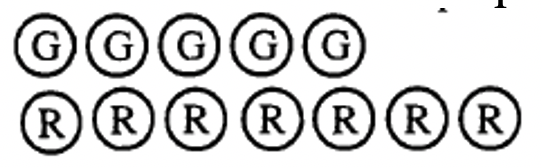 |
b. La siguiente colección representa _____ 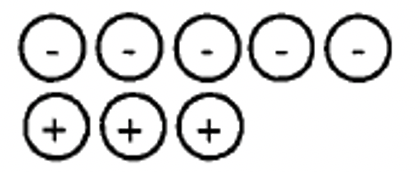 |
|
c. La siguiente colección representa _____ 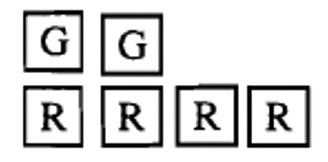 |
d. La siguiente colección representa _____ 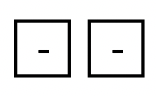 |
|
e. La siguiente colección representa _____ RRRRRRGGG |
f. La siguiente colección representa _____ GRRGRRGGGGG |
|
g. La siguiente colección representa _____ 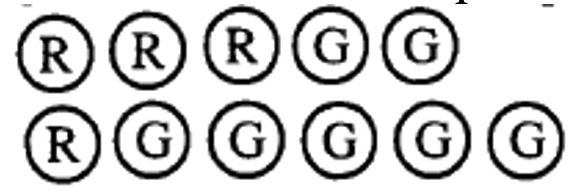 |
h. La siguiente colección representa _____ 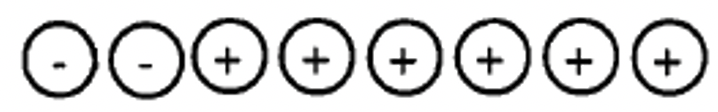 |
¿Cómo crees que lo hiciste? Ojalá se te ocurriera una respuesta de -2 para a-d. Si es así, debes estar convencido de que diferentes colecciones pueden representar el mismo número. Cada emparejamiento de un negativo con un positivo básicamente “se cancela entre sí”. Por lo tanto, para averiguar qué número representa una colección en particular, simplemente empareja tantos positivos con negativos como sea posible (pares rojo-verde), y elimine o ignore esos contadores. Después, cuente los contadores del “color” o “signo” que queda. Te habrás dado cuenta de que era más fácil calcular a-d porque los emparejamientos se veían más fácilmente.
Usando contadores positivos y negativos, encuentra 3 representaciones diferentes de 4. Hazlo primero con tus manipuladores positivos y negativos reales. Después, muéstralo en papel.
| a. | b. | c. |
Usando contadores positivos (verde) y negativos (rojos), se muestran 3 representaciones diferentes de -4. Entonces, muestra tus tres representaciones diferentes a continuación.
| a. | b. | c. |
Pasemos a cómo podemos usar los contadores para sumar enteros. Para agregar enteros, simplemente haga una colección de contadores que represente cada número a agregar y combine los contadores. Después, encuentra el número que representa la colección resultante. Haz esto primero emparejando cualquier positivo y negativo y eliminándolos de la pila.
Mostrar dos formas diferentes de usar los contadores para sumar los 4 + (-7).
Primera Vía:
Primero, combine una colección que represente 4 (4G) y una colección que represente -7 (7R):
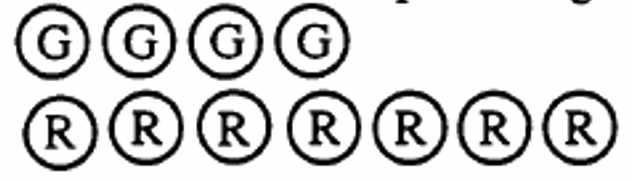
En segundo lugar, elimine cualquier par rojo-verde:
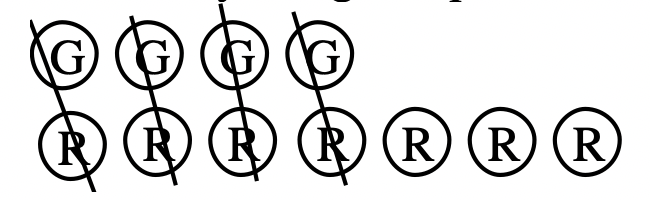
Tercero, contar los contadores restantes:
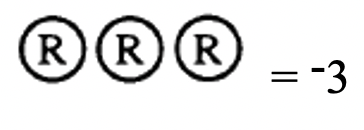
Por lo tanto, 4 + (-7) = -3.
Segunda Vía:
Primero, combine una colección que represente 4 (8G y 4R) y una colección que represente 7 (8R y 1G):
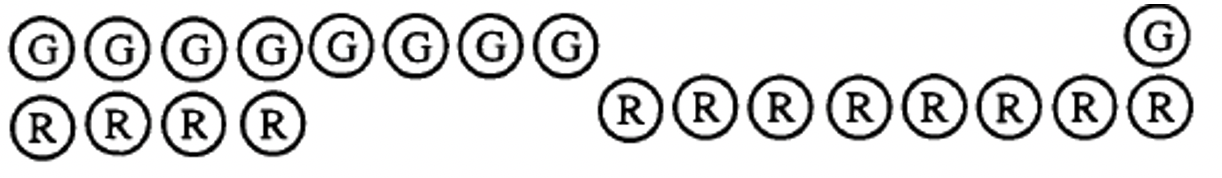
En segundo lugar, elimine cualquier par rojo-verde:
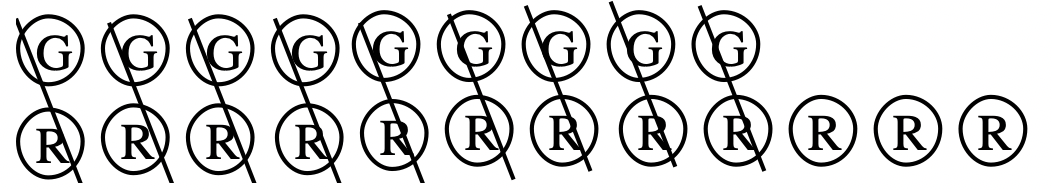
Tercero, cuente qué contadores quedan:

Por lo tanto, 4 + (-7) = -3.
Por supuesto, el método más simple y directo es la primera forma mostrada, pero el resultado es el mismo incluso cuando se utilizan representaciones complicadas de los números en el primer paso.
Utilice los contadores rojo y verde para agregar los siguientes números enteros. Haz estos problemas usando los manipuladores reales. Luego, explica y muestra los pasos a continuación
Aunque la resta es un poco más complicada usando contadores, proporcionan una manera realmente interesante de mostrar cómo restar números negativos.
Usando los contadores, m — n significa eliminar una colección de contadores que representan n de una colección de contadores que representan m. El número que representa la colección resultante es la diferencia (respuesta).
Esto significa que tenemos que comenzar con una colección de contadores que representen m. Para eliminar una colección que represente n, debe ser posible eliminar una colección que represente n de la colección utilizada para m. A veces, la colección original elegida para m no será suficiente, y la colección debe ser alterada agregando algunos pares rojo-verdes a la colección que representan m. Por lo general, comenzamos poniendo una representación simple de m contadores y vemos si es posible eliminar o quitar una representación de n contadores. Si es así, hacemos que y encontramos el número que representa la colección resultante. Probemos esto en algunos ejemplos usando los modelos físicos (manipulativos) y luego practiquemos mostrándolo en papel.
4 — 2
Esto significa eliminar una colección que representa 2 de una colección que representa 4.
Paso 1: Hacer una colección que represente 4 (4 contadores verdes):\(\not{GG}\) GG
Paso 2: Saca una colección que represente 2 (2 contadores verdes):
Paso 3: La colección restante (GG) representa 2. Entonces, 4 — 2 = 2.
-5 — (-3)
Esto significa eliminar una colección que representa -3 de una colección que representa -5.
Paso 1: Hacer una colección que represente -5 (5 contadores rojos): RRRRR
Paso 2: Saca una colección que represente -3 (3 contadores rojos):
Paso 3: La colección restante (RR) representa -2. Entonces, -5 — (-3) = -2.
3 — 5
Esto significa eliminar una colección que representa 5 de una colección que representa 3.
Paso 1: Hacer una colección que represente 3 (3 contadores verdes): GGG
¡OH NO! El siguiente paso sería sacar una representación de 5 (5 contadores verdes), pero fíjese que esto es imposible porque para empezar solo hay 3 contadores verdes. Aquí se debe insertar un paso extra. Necesitamos alterar la representación de 3 para que se puedan sacar 5 greens. Debe tener sentido que siempre podamos insertar algunos pares verde-rojo a la representación de 3 (cada par verde-rojo es el efecto de sumar cero) sin cambiar la representación de 3. En este ejemplo, tiene sentido agregar 2 pares rojo-verdes más, para que haya 5 verdes y 2 rojos en la colección. Seguirá siendo una colección que representa a 3. Este paso extra suele ser necesario a la hora de hacer problemas de resta con números enteros.
Paso 2: Agregar 2 pares rojo-verde a la colección que representan 3: GGGRGRG
Paso 3: Saca una colección que represente 5 (5 contadores verdes):\(\begin{aligned} & \fbox{GGGGG} \\ & \text{RR} \end{aligned}\)
Paso 4: La colección restante (RR) representa -2. Entonces, 3 — 5 = -2
Para cada problema, establezca lo que significa el problema (Por ejemplo, 4 — (- 9) significa eliminar una colección de contadores que representan -9 de una colección de contadores que representan 4), y luego explicar y mostrar cada paso que necesita tomar para encontrar la respuesta. Cada problema requiere de 3 o 4 pasos. Debes hacer estos problemas usando los manipuladores, y a medida que lo haces, explicar y mostrar los pasos en papel.
|
a. 6 — 3 Esto significa Mostrar todos los pasos a continuación. |
|
b. 4 — 6 Esto significa Mostrar todos los pasos a continuación. |
|
c. -7 — (- 6) Esto significa Mostrar todos los pasos a continuación. |
|
d. -3 — (- 7) Esto significa Mostrar todos los pasos a continuación. |
|
e. 4 — (- 3) Esto significa Mostrar todos los pasos a continuación. |
|
f. -2 — 5 Esto significa Mostrar todos los pasos a continuación. |
|
g. 5 — 5 Esto significa Mostrar todos los pasos a continuación. |
|
h. 5 — (- 5) Esto significa Mostrar todos los pasos a continuación. |
|
i. -4 — (- 4) Esto significa Mostrar todos los pasos a continuación. |
|
j. -6 — 6 Esto significa Mostrar todos los pasos a continuación. |
Indique qué significa el problema en términos de usar contadores positivos y negativos y mostrar todos los pasos para (a) restar 5 - 8, y luego (b) sumar 5 + (-8).
| a. 5 — 8 |
| c. ¿Qué notaste de tus respuestas a a y b? |
Esperemos que hayas notado que al eliminar una colección que representa 8 de una colección que representa 5 se obtiene el mismo resultado que combinar una colección que representa 5 y -8.
Es decir, restar 8 produjo el mismo resultado que sumar -8.
- Usa los manipuladores reales. Comienza con una colección de al menos 4 contadores rojos y algunos verdes y escribe lo que tienes a continuación:
- Elimina 4 contadores rojos de tu colección. Muestra este paso tachando o dando vueltas a 4 mostradores rojos en tu colección anterior. Después de eliminar esos contadores rojos, ¿qué número representa ahora la colección en la parte a? ______
- Empezar de nuevo. Comienza combinando la colección original que tenías en la parte a con 4 contadores verdes (agrega 4 contadores verdes a tu colección original). A continuación, muestra cómo se ve ahora la colección.
- ¿Qué número representa tu colección final? ______
Los ejercicios 21 y 22 ilustran un dato muy importante sobre la resta. Restar un número da el mismo resultado que sumar el número opuesto. Los ejercicios 10 y 13, y los ejemplos que precedieron a cada uno de esos ejercicios también ilustraron este hecho.
Tenga en cuenta que los contadores rojo y verde, o los contadores positivos y negativos son opuestos.
Explica lo que significa 7 — 4, y luego indica otra forma de obtener el mismo resultado.
Solución
7 — 4 significa eliminar una colección que representa 4 de una colección que representa 7. Esto da el mismo resultado que combinar una colección que representa 7 con una colección que representa lo contrario de 4, que es combinar una colección que representa 7 con una colección que representa -4 (lo que significa combinar 7G con 4R). Entonces, 7 — 4 = 7 + (- 4).
Explica lo que significa 2 — (- 6), y luego indica otra forma de obtener el mismo resultado.
Solución
2 — (- 6) significa eliminar una colección que representa -6 de una colección
representando 2. Esto da el mismo resultado que combinar una colección que representa 2 con una colección que representa lo contrario de -6, que es combinar una colección que representa 2 con una colección que representa 6 (lo que significa combinar 2G con 6G). Entonces, 2 — (- 6) = 2 + 6.
Explicar lo que significa cada problema y luego indicar otra forma de obtener el mismo resultado
| b. 4 — 8 |
Reescribir cada resta como un problema de suma equivalente.
| a. 4 — 5 = _____________ |
Reescribe cada problema para que sea sólo en términos de adición. En otras palabras, sólo cambiar cada parte de resta por una parte de suma equivalente. No compute la respuesta.
Rellene los espacios en blanco:
- Restar 6 es lo mismo que sumar _____.
- Restar -8 es lo mismo que sumar _____.
- Restar un número positivo es lo mismo que sumar un número ______________, donde ese número _____________ es lo opuesto al número positivo original.
- Restar un número negativo es lo mismo que sumar un número ______________, donde ese número _____________ es lo opuesto al número negativo original.
- Restar un número es lo mismo que sumar el _______________ de ese número.
Lo único a lo que debes prestar mucha atención es la diferencia entre el signo de resta y el número que se está restando. Cuando reescribes un problema de resta como un problema de suma equivalente, tienes que recordar cambiar el número que estaba siendo
restado a su opuesto. Ciertamente no es cierto que 6 — 3 sea lo mismo que 6 + 3. Pero es cierto que 6 menos (positivo 3) es igual a 6 más (negativo 3); o 6 — 3 = 6 + (- 3).
No es necesario cambiar los problemas de resta por problemas de suma equivalentes. Sin embargo, a veces es muy útil porque puede ser más fácil trabajar con el problema de la adición. Y si toda resta puede escribirse como suma, entonces uno solo necesita aprender reglas para sumar y aplicarlas a todos los problemas de suma o resta. Permítanme decir que aunque es una buena idea conocer las reglas de suma y resta, es aún más importante poder volver a los conceptos básicos y poder usar manipuladores para entender lo que realmente significan la suma y la resta.
Si rellenaste la respuesta correcta al 28e, entonces la tienes. La relación entre suma y resta radica en este hecho.
Cada problema de resta se puede reescribir como un problema de suma equivalente. En lugar de restar un número, puedes sumar lo contrario de ese número.
Definición: Sea m y n cualquier entero. Entonces, m — n = m + (- n). Esto se llama Agregar lo contrario. Recuerda: -n no es necesariamente negativo! Si n es positivo, -n es negativo pero si n resulta ser negativo (n es solo una variable), entonces -n sería positivo.
Volvamos a la línea numérica y usando vectores junto con el enfoque de addend faltante para calcular un problema de resta. Tenga en cuenta que este es un enfoque completamente diferente de la forma en que lo hicimos al inicio del conjunto de ejercicios, cuando lo hicimos con acciones de hacer y deshacer. Primero, revisemos la definición de resta utilizando el enfoque de addend faltante.
Definición: Resta (Missing Addend Approach) La diferencia de dos números, m y n, escritos m — n es el número c tal que n + c = m. En otras palabras, si se suma c al sustraendo, n, entonces la suma es el minuendo, m. A la respuesta, c, se le llama la adición faltante.
Considerar el problema 7 — 3. El enfoque de adición faltante establece que la respuesta a este problema de resta será el número que cuando se suma al número que se muestra después del signo de resta es igual al número que precede al signo de resta. Ya que 3 es el número después del signo de resta, tenemos que encontrar un número para sumar a 3 que dará una respuesta de 7. Usando una línea numérica, esto significa que si colocas el punto inicial de un vector en 3, ¿qué vector debe dibujarse (el agregado faltante todavía se puede considerar como qué acción debe tener lugar) para que el punto terminal aterrice en 7? Dibuja un vector con su punto inicial en 3 y su punto terminal en 7. Asegúrese de que la flecha al final del vector apunte a 7.
El número que representa el vector es la respuesta al problema. Estamos tratando de encontrar esa adición faltante, que es el vector que dibujamos. A continuación se muestra la ilustración para 7 — 3. El vector tiene longitud 4 y apunta a la derecha, por lo que la respuesta es 4, que he escrito encima del vector (etiquetado y marcado el addend faltante) para indicar la respuesta al problema.

Nuevamente, tenga en cuenta que este es un enfoque completamente diferente para la resta. No es en absoluto como la forma en que lo hicimos al inicio del conjunto de ejercicios, cuando lo hicimos haciendo una acción, y luego deshaciendo otra y luego viendo qué acción podría haber logrado el mismo resultado.
Usando el enfoque de addend faltante, solo se muestra un vector, y el número que representa el vector es la respuesta al problema. En otras palabras, el vector representa el addend faltante que estás buscando, que es la diferencia de los dos números. Puede encontrar la respuesta al problema de resta dibujando un vector, colocando el punto inicial del vector en el sustraendo (el número que se muestra justo después del signo de resta) y colocando el punto terminal en el minuendo (el número que precede al signo de resta). Tenga en cuenta que esta definición sólo tiene sentido al restar dos números, a diferencia de sumar y/o restar varios números.
Procedimiento para restar dos enteros usando vectores y el enfoque de addend faltante: Para encontrar la diferencia de m y n, dibuje un vector con su punto inicial en n y su punto terminal en m. El vector dibujado es el addend faltante, y es la respuesta al problema: m — n.
Es importante distinguir entre el signo de resta y el sustraendo (el número que se muestra después del signo de resta). También es importante recordar poner el punto inicial del vector que representará la suma faltante en el sustraendo (el número DESPUÉS del signo de resta, y el punto terminal en el minuendo (el número que se muestra PRECEDENTE al signo de resta). Un método que a veces uso es rodear el minuendo y restar y luego dibujar una flecha desde el sustraendo hasta el minuendo así recuerdo dibujar el vector con su punto inicial en el sustraendo y su punto terminal en el minuendo.
Probemos el problema 2 — 9. Entonces, 9 + ____ = 2. Circula el minuendo y restando y dibuja una flecha desde el sustraendo hasta el minuendo antes de dibujar el vector.
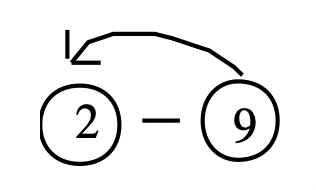
En la recta numérica, dibuje un vector con su punto inicial en 9 y su punto terminal en 2. El vector dirigido dibujado representa la respuesta: -7.
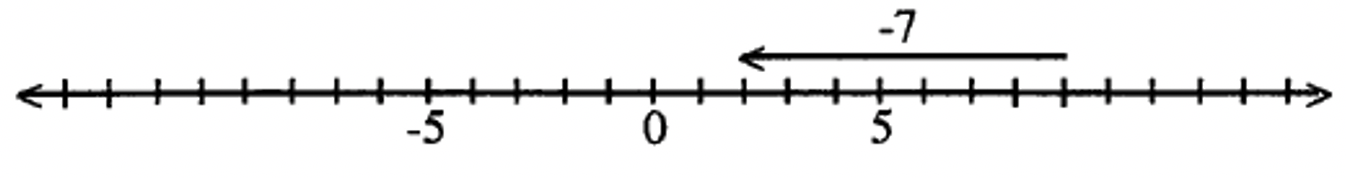
12 — (- 8). Entonces, -8 + ____ = 12.
Circula el minuendo y restando y dibuja una flecha desde el sustraendo hasta el minuendo antes de dibujar el vector.
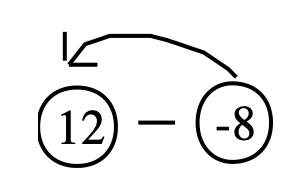
Tenga en cuenta que cuando dibuja una flecha desde el sustraendo hasta el minuendo, la flecha apunta a la izquierda en el problema de resta real. Pero eso NADA tiene que ver con si la flecha en el vector que dibujas en la recta numérica apuntará o no a la izquierda o a la derecha. Señala al minuendo. Para este ejemplo, tenga en cuenta que en el vector addend faltante dibujado a continuación, apunta a la derecha, y que la respuesta a este problema es un número positivo.
Coloque el punto inicial del vector en -8 y el punto terminal en 12. El vector dibujado a continuación muestra la respuesta: 20.
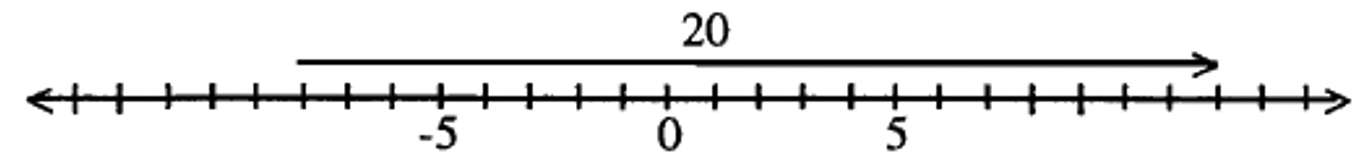
Antes de continuar, piense en la posibilidad de usar el enfoque de addend faltante y ni siquiera obtener un vector.
- En otras palabras, ¿y si el punto inicial y terminal del vector estuviera en el mismo número? Parecería un punto, no un vector. ¿Cuándo sucedería esto?
- ¿Cuál sería la respuesta a un problema donde ocurrió esto?
Encuentre la respuesta a los siguientes problemas de resta usando vectores en la línea numérica junto con el enfoque de adición faltante. Dibuja una flecha desde el sustraendo hasta el minuendo como se muestra en los dos últimos ejemplos. Antes de dibujar el agregado faltante que representa la respuesta al problema, etiquete y marque su línea numérica con al menos 0 y un punto a cada lado de cero. Después, dibuja el vector que represente la respuesta a cada problema y etiquete el vector con ese número.
|
a. 10 — 4 = ______  |
|
b. -7 — 5 = ______  |
|
c. 8 — (- 3) = ______  |
|
d. -9 — (- 1) = ______  |
|
e. 3 — 10 = ______  |
|
f. -5 — (- 8) = ______  |
|
g. 6 — (- 6) = ______  |
|
h. 9-9 = ______  |
Al observar los vectores a - c a continuación, averigüe qué problema de resta se estaba realizando, y luego indique la respuesta. Por ejemplo, el vector d vino de hacer el problema -1 — 5 ya que el punto inicial de ese vector está en 5 y el punto terminal está en -1. Dado que el vector d tiene 6 unidades de largo y va a la izquierda, representa el número -6. Por lo tanto, el vector d sería: -1 — 5 = -6.
| a. Vector a: | b. Vector b: | c. Vector c: |

Una cosa que me encanta de usar el modelo de addend faltante para mostrar la resta es que funciona igualmente bien al restar con enteros más grandes. Apenas aproximado donde están los enteros en la recta numérica en relación con ellos mismos y cero. La respuesta tiene sentido usando el modelo.
Los siguientes ejemplos muestran cómo usar vectores en la recta numérica junto con el enfoque de addend faltante para encontrar estas diferencias: 58 — 87, -130 — 55 y -130 — -55.
58 — 87.
Solución
Dibuja un vector del 87 al 58. Dado que el vector apunta hacia la izquierda, la respuesta es negativa y la longitud del vector es de 29 unidades de largo, 87 — 58. Entonces, 58 — 87 = -29.

-130 — 55.
Solución
Dibuja un vector de 55 a -130. Dado que el vector está apuntando a la izquierda, la respuesta es negativa y la longitud del vector es de 185 unidades de largo, ya que es de 130 unidades de -130 a 0 más otras 55 unidades de 0 a 55. Entonces, -130 — 55 = -185.
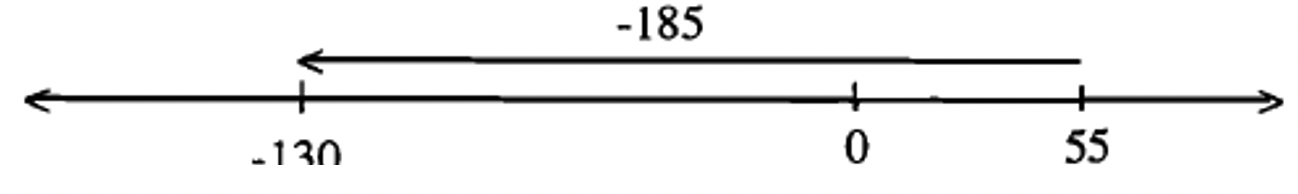
-55 — (-130).
Dibuja un vector de -130 a -55. Dado que el vector apunta hacia la derecha, la respuesta es positiva y la longitud del vector es de 130 — 55, o 75 unidades de largo. Entonces, -55 — (-130) = 75.

Marcar y etiquetar una recta numérica con al menos cero, el minuendo (el número delante del signo de resta) y el sustraendo (el número que se resta). Entonces, usa un vector para encontrar la respuesta al problema. Etiquetar el vector que es la respuesta
|
a. -92 — (-71) = _______  |
|
b. 92 — (- 81) = _______  |
|
c. -110 — (- 200) = _______  |
|
d. -122 — 76 = _______  |
|
e. 208 — 389 = _______  |
Por último, aquí hay un conjunto de reglas que siempre se pueden utilizar para sumar y restar enteros sin el uso de manipuladores. Si bien estas reglas siempre funcionarán, es mejor entender primero de dónde provienen estas reglas y por qué funcionan. De hacer los ejercicios en este conjunto de ejercicios, ahora deberías tener una mejor comprensión de lo que significa sumar y restar con números positivos y negativos.
- Cualquier problema de resta se puede reescribir como un problema de suma equivalente usando la definición de agregar lo contrario. Una vez que todos los problemas de resta se reescriben como problemas de suma equivalente, solo hay que sumar, y por lo tanto, solo necesitamos reglas para sumar, que siguen.
- Para sumar números que tengan signos similares (ya sea todos positivos o todos negativos), agregue los valores absolutos de los números. El signo de la respuesta será el signo de los números originales.
- Para sumar dos números con signos distintos (uno positivo y otro negativo), tomar la diferencia de los valores absolutos de los dos números. El signo de la respuesta será el mismo que el signo del número con el mayor valor absoluto. Si los valores absolutos de los números son los mismos, la respuesta es cero.
Nunca me gustó mucho la forma en que estaban redactadas estas definiciones, pero esta es la forma matemática de expresar exactamente cómo obtener la respuesta. Así es como pienso acerca de las reglas.
Primero, generalmente reescribo cada resta como un problema de suma equivalente, a menos que se estén restando dos números enteros. En ese caso, si el primer número entero es mayor que el segundo número entero, hago una resta regular de números enteros. Si el número entero mayor se está restando del número entero menor, sé que la respuesta es negativa y simplemente poner un número negativo delante de la respuesta.
Así es como pienso en sumar números que tengan signos similares:
- Digamos que estabas sumando 8 + 9. Ambos son positivos. Así que solo se suman los dos números enteros como de costumbre, y la respuesta sigue siendo positiva. Es como tener 8 dólares en el banco, y depositar 9 dólares más. Ahora tienes 17 dólares en el banco. Entonces, espero que no sea de sorprender que 8 + 9 = 17.
- Digamos que estabas sumando -8 + (- 9). Ambos son negativos. Esto es como estar endeudado, e ir más profundo en el departamento Así que solo se suman los dos números enteros como de costumbre, pero la respuesta es negativa. Es como adeudarle 8 dólares a alguien, y luego pedir prestados 9 dólares más. Ahora le debes a esa persona 17 dólares. Entonces, -8 + (- 9) = - 17.
Así es como pienso en sumar números que tengan signos distintos.
- Digamos que estabas sumando 24 + (-10). Ahora bien, este es un ejemplo de sumar dos números con signos distintos. Como los signos son DIFERENTES, ignoro sus signos y tomo su DIFERENCIA —eso es lo mismo que simplemente restar sus valores absolutos. Cuando hago caso omiso de sus signos, resto el número menor del número mayor. Entonces, para determinar si el signo de la respuesta es positivo o negativo, veo cuál supera al otro (¿hay más negativos o positivos?) — eso es lo mismo que tomar el signo del que tiene el valor absoluto. 24 + (-10) podría pensarse como tener 24 dólares en el banco y escribir un cheque por 10 dólares. Aún te quedan 14 dólares en el banco. Entonces, 24 + (-10) = 14.
- Si estuvieras agregando -24 + 10, el problema se haría igual que el anterior excepto que en este caso, los negativos superan a los positivos, por lo que la respuesta final es negativa. Es como adeudarle 24 dólares a alguien y pagarle 10 dólares. Ahora, sólo les debes 14 dólares. Entonces, -24 + 10 = -14.
- Digamos que estabas sumando 14 + -14 o sumando -83 + 83. En ambos ejemplos, estoy agregando opuestos. En cierto modo, uno deshace al otro. Entonces ambos son iguales a cero. Esto también se podría hacer pensando en qué signo supera al otro. Pero ninguno supera al otro, y esa es otra razón por la que la respuesta no es ni negativa ni positiva, sino que es cero.
Usando las reglas al inicio de la página anterior, o la forma en que pienso al respecto, o tal vez alguna otra forma en que lo pienses que estás seguro funciona y tiene sentido, deberías poder sumar y restar enteros con confianza. Debes ser capaz de explicar el significado de las operaciones, y poder usar manipulativos y líneas numéricos para ayudar a otros a aprender a sumar y restar con enteros y entender
Realice los siguientes problemas aritméticos cambiando primero la resta para sumar lo contrario. Después suma dos números a la vez, trabajando de izquierda a derecha. Muestra tus pasos.
Realice los siguientes problemas aritméticos cambiando primero la resta para sumar lo contrario. Después suma números con signos similares para que tengas la suma de un número positivo y otro negativo. Después sumar esos dos números juntos. Muestra tus pasos.
Recuerde que para que un conjunto se cierre bajo suma, la suma de dos elementos cualesquiera en el conjunto siempre estará en el conjunto. Para que un conjunto se cierre bajo resta, la diferencia de dos elementos cualesquiera en el conjunto siempre estará en el conjunto. Para probar que un conjunto no está cerrado bajo suma o resta, es necesario proporcionar un contraejemplo.
Para cada uno de los siguientes conjuntos, determine si el conjunto está cerrado bajo la operación dada. Proporcionar un contraejemplo si no está cerrado
| a. ¿Enteros en adición? | b. ¿Enteros bajo sustracción? |
| c. ¿Enteros positivos en suma? | d. ¿Enteros positivos bajo resta? |
| e. ¿Enteros negativos en suma? | f. ¿Números enteros negativos bajo resta? |
| g. {-1, 0, 1} bajo adición? | h. {-1, 0, 1} bajo resta? |


