7.2: algoritmos de división
- Page ID
- 113237
Como hemos visto, la división puede ser vista como lo opuesto a la multiplicación.
Otra forma de pensarlo es como SUTRACCIÓN REPETIDA.
¡Hagamos DIVISIÓN de la Manera Fácil!
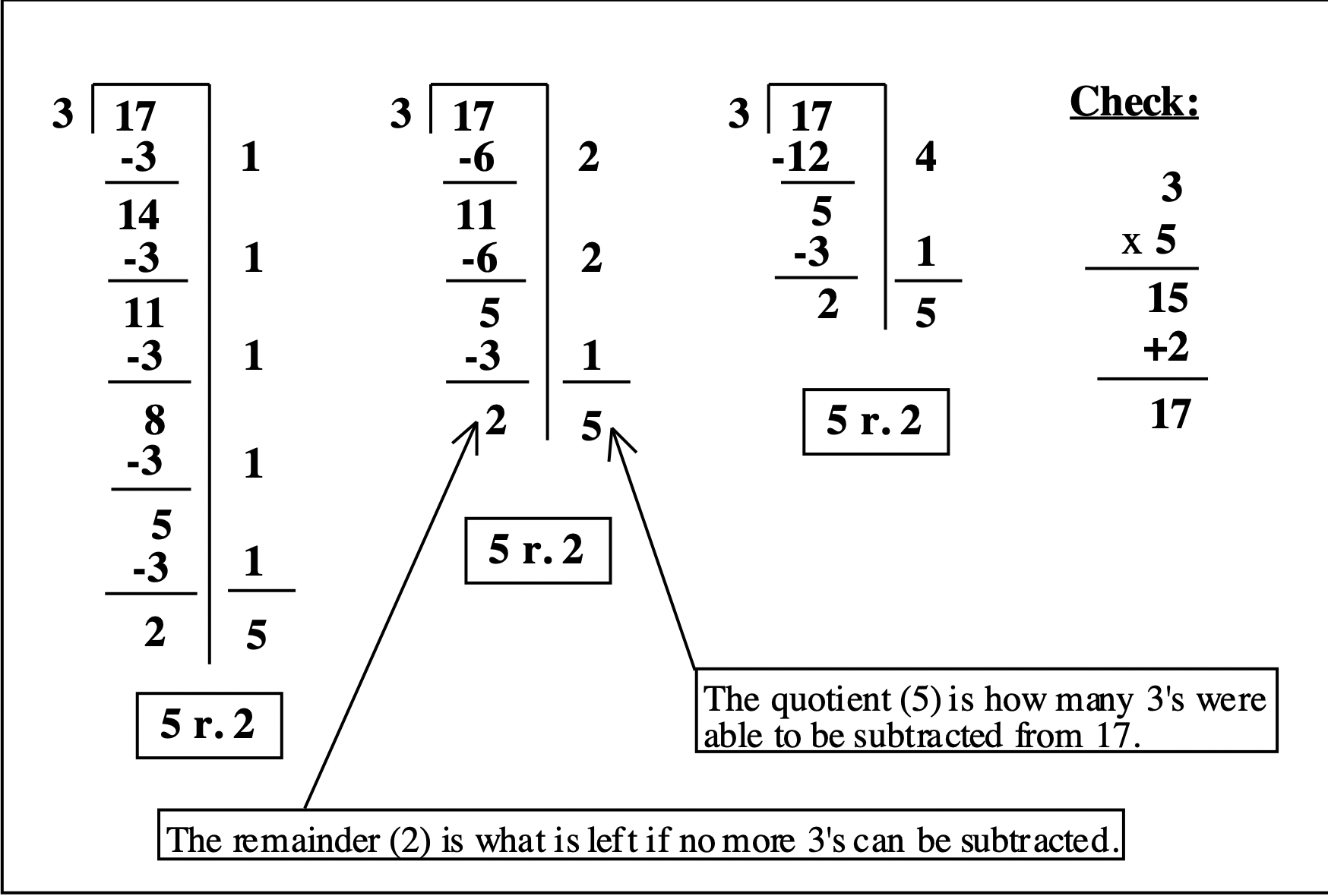
Así es. La división es realmente solo “resta repetida”. Si se te pide dividir 17 por 3, que está escrito\(17 \div 3\), tienes que averiguar cuántos 3 se pueden restar de 17. Probablemente ya sepas que la respuesta es 5 r. 2, pero veamos cómo funciona esto contando cuántas veces se puede restar 3 de 17. Mira el trabajo a continuación. Se muestran tres formas diferentes. Haces un andamio (parece un ahorcado) y haces un seguimiento de cuántos 3 restas en cada paso a la derecha del andamio. En el primero, 3 se resta uno a la vez, y se restaron un total de cinco 3's. En la segunda se restan los dos primeros 3, luego se restan 1 más, luego 2 más, para restar un total de cinco 3's. En el tercero, se restan cuatro 3's, y luego 1 más, nuevamente para restar un total de cinco 3's. Cada vez que restes, mira para ver qué número queda. Si es 3 o más, puedes restar algunos más 3's Pero cuando obtienes un número menor que 3, sabes que 3 ya no se puede restar, así que ese es tu resto. Para este problema, 2 fue el resto. Necesitas contar cuántos 3 has restado. A la derecha del andamio, escribes cuántos 3 estás restando a medida que avanzas. Simplemente agrega esos números para averiguar cuántos 3 has restado. La respuesta al problema es cuántos 3 le restaste, y luego necesitas escribir también el resto. En este caso,\(17 \div 3 = 5\) r. 2. Siempre revisa tu respuesta mi multiplicando el divisor (3) por el cociente (5) y sumando el resto (2):\(3 \times 5 + 2 = 15 + 2 = 17\). ¡Comproba!
Hacer división larga con grandes números suele ser difícil porque tienes que multiplicar en tu cabeza, y es fácil cometer errores. Pero, al usar este nuevo método de resta repetida, junto con una multiplicación parcial te inventas antes de tiempo usando suma repetida, nunca tienes que multiplicar en tu cabeza (ni multiplicar en absoluto), y nunca tienes que adivinar cuántas veces un número “entra” en otro número. Este método toma un poco más de papel, pero facilita el problema y es prácticamente infalible. A mucha gente no le gusta hacer división larga, porque es difícil adivinar siempre el número exacto correcto y a veces les duele la cabeza por pensar demasiado. Vamos a eliminar ese problema. Lo importante es que sepas lo que significa división (resta repetida), sabes cómo obtener la respuesta correcta usando un método que tenga sentido para ti, y sepas cómo verificar tu respuesta para asegurarte de que sea correcta.
Bien, entonces digamos que tuviste que hacer este problema de división:\(361 \div 53\).
¡YUK! Esto no parece divertido. En realidad, todo esto que se pregunta es cuántos 53 se pueden restar de 361. Podemos restar 53 uno a la vez, pero podría llevar mucho tiempo. Podríamos decidir restar más de un 53 a la vez.
Antes de hacer la división, hagamos una tabla de multiplicación parcial rápida para 53, ¡usando ADICIÓN REPETIDA! Esta mesa es tu trabajo de preparación para la división. Una forma sencilla de componer una tabla de multiplicación parcial para 53 sin multiplicar nunca implica duplicar números. Eso lo sabemos\(1 \times 53 = 53\). Para averiguarlo\(2 \times 53\), basta con sumar dos 53's juntos. Dos 53 agregados a dos 53 más equivaldrían a cuatro 53's, o\(4 \times 53\). Cuatro 53 sumadas a cuatro 53 más equivaldrían a ocho 53's, o\(8 \times 53\). Bien, entonces, ¿cómo muestras esto? Comienza con un 53 y duplica para encontrar dos 53's. Duplica ese número para encontrar cuatro 53's. Duplica ese número para encontrar ocho 53's. Mira en la parte izquierda del cuadro que se muestra a continuación. Mira como hay un 1 apuntando al 53 eso significa\(1 \times 53\). Si duplicas el 53, (53 + 53), entonces ya lo sabes\(2 \times 53 = 106\), así que un 2 puntos a 106. Si se duplica eso (106 + 106), ya lo sabe\(4 \times 53 = 212\), así que un 4 puntos a 212. Y si duplicas este número (212 + 212), entonces ya lo sabes\(8 \times 53 = 424\), así que un 8 puntos al 424. ¿No es esa una manera fácil de encontrar\(8 \times 53\)? Pero lo genial es que tú también sabes\(8 \times 53\) ¡\(1 \times 53, 2 \times 53, 4 \times 53,\)Y! Esto es útil para saber hacer la división larga. En lugar de adivinar cuántas veces 53 “entra” 361, notamos cuántas 53 se pueden restar de 361 (subestimar está bien). ¡Tampoco hay que hacer multiplicación en tu cabeza! El cuadro de la derecha muestra cómo usar la resta repetida para hacer el problema de división:\(361 \div 53\). Primero, conforman una tabla de multiplicación parcial. Después, escribe el problema de división usando un andamio. Mira la tabla de multiplicar y elige el número más grande que puedas restar del 361, que es el 212. Resta 212 de 361 y escribe 4 a la derecha porque acabas de restar 4 53's El número más grande que puedes restar de 149 es 106. Si haces eso, has restado 2 53 más, así que escribe un 2 a la derecha. Después de restar, quedan 43 y no se pueden restar más 53's. Por lo tanto, 43 es el resto. Agrega los números de la derecha para ver cuántos 53 has restado. La respuesta es 6 r. 43. Para verificar, multiplicar\(53 \times 6\) y sumar 43. La respuesta es 361.
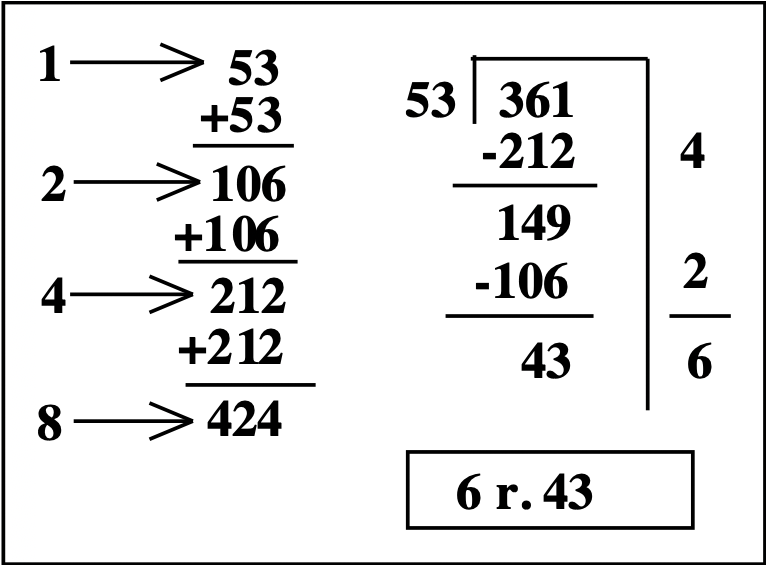
P.S. Puedes multiplicar 53 veces 6 sumando 106 + 106 + 106, ya que eso es dos 53's sumadas 3 veces, que es seis 53's!!!
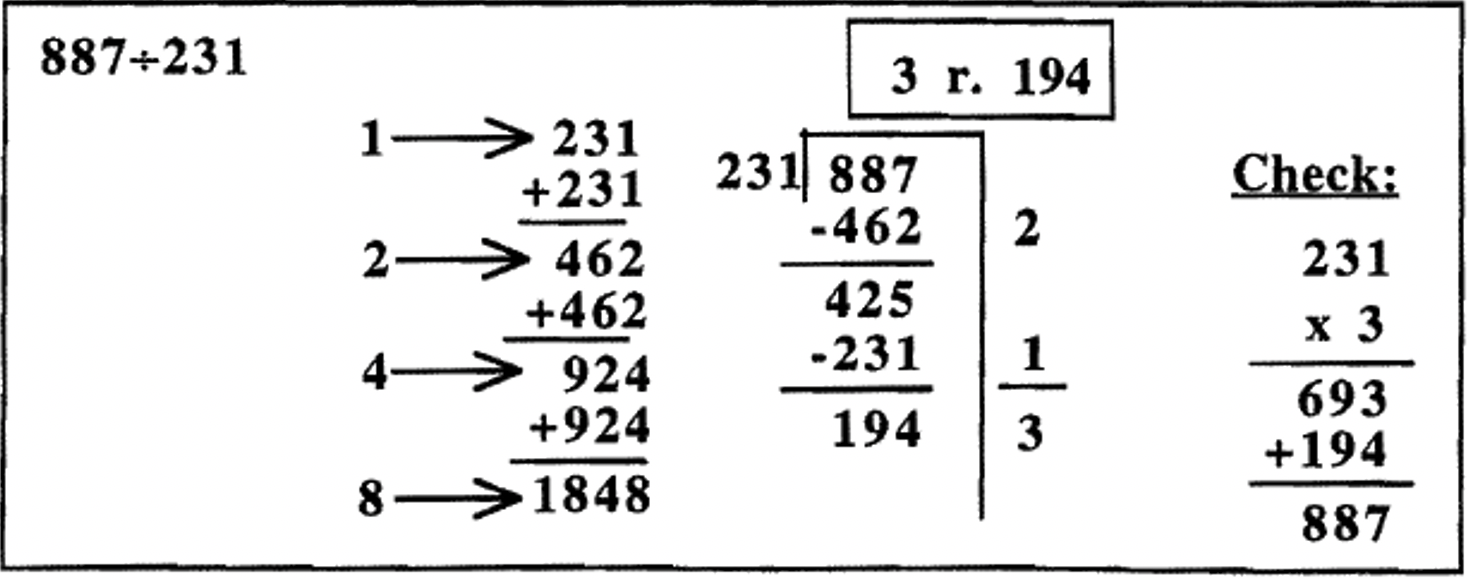
A continuación te presentamos algunos ejemplos más para que los estudies. Primero se compone una tabla de multiplicación parcial. Este trabajo de preparación que implica algunas adiciones hace que la división sea mucho más fácil. Entonces, el problema se hace usando resta repetida (con ayuda de la tabla de multiplicación parcial) usando un andamio. Después de sumar cuántas veces se restó el divisor del dividendo (los números a la derecha del andamio), la respuesta (cociente y resto) se escribe en una casilla arriba del problema. Por último, se muestra el cheque. También, verifique para asegurarse de que el resto sea menor que el divisor.
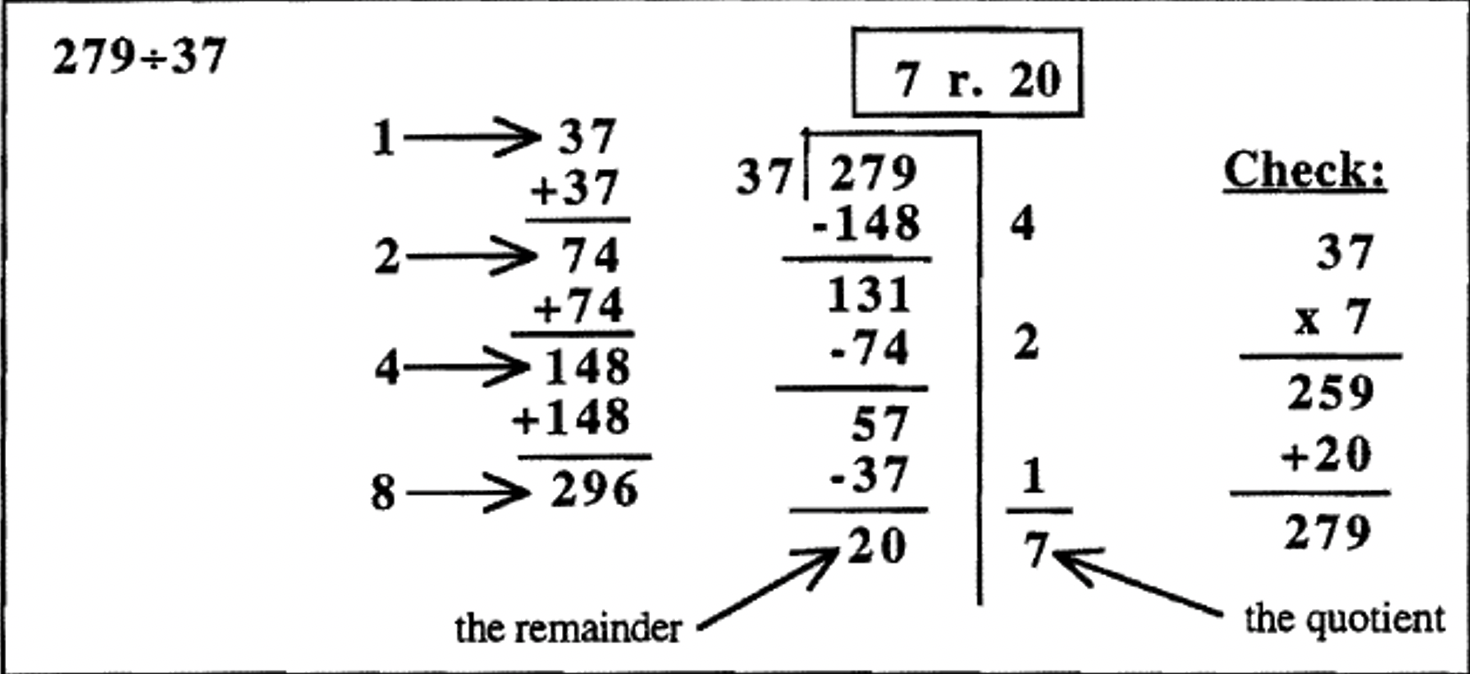
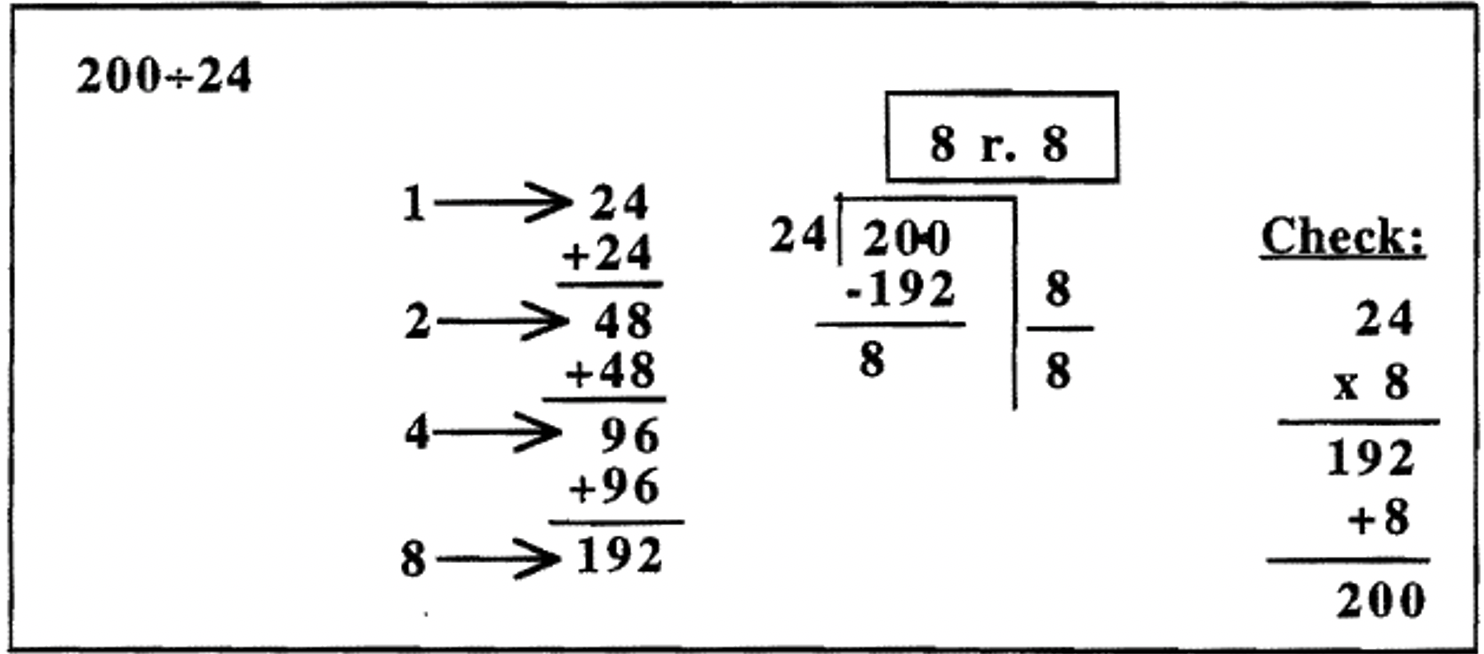
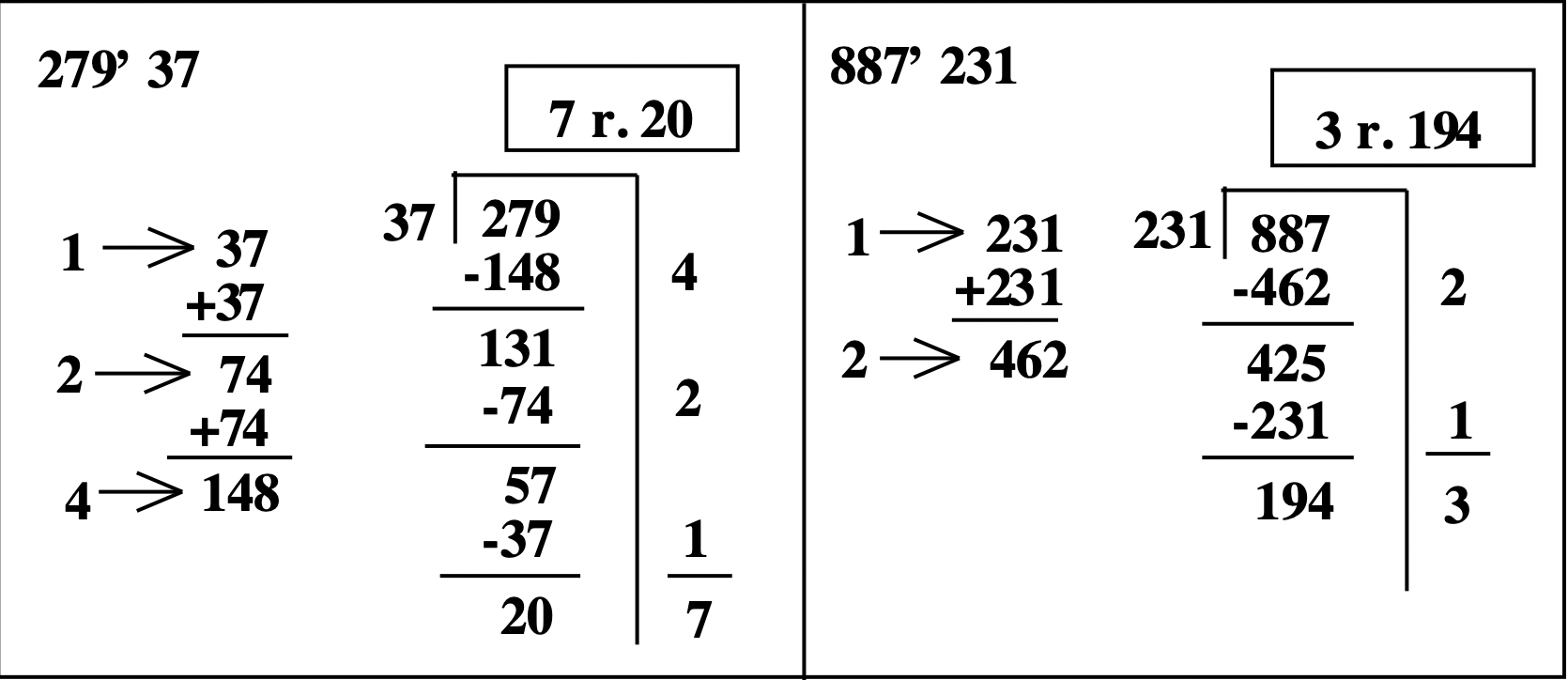
En los ejemplos hasta el momento, todos los cocientes fueron menores a 10. Es posible seguir duplicando el divisor en la tabla de multiplicación parcial, para que puedas encontrar el divisor por cualquier potencia de 2 — 1, 2, 4, 8, 16, 32, 64, etc. Dejarías de duplicar si notas que duplicar una vez más da un número mayor que el cociente. De hecho, en el primer ejemplo de la página anterior,\(279 \div 37\), realmente no tuve que duplicar 148 para averiguarlo\(8 \times 37\), ya que duplicar 148 me da un número mayor que 279. En el tercer ejemplo,\(887 \div 231\), no tuve que duplicar 462 para averiguarlo\(4 \times 231\), ya que duplicar 462 da un número mayor que 887. Los problemas podrían haberse acortado ligeramente si me hubiera dado cuenta de eso antes de tiempo. Se verían así (se omite el cheque).
Bien, ahora que has estudiado algunos ejemplos, es hora de que intentes usar este método. Los primeros cuatro problemas son exactamente los mismos que se hicieron en los ejemplos anteriores. Si te quedas atascado, mira hacia atrás en ellos y copia cómo los hice en otro trozo de papel. Entonces, inténtalo de nuevo.
Para cada problema de división, haz tu trabajo de preparación usando el método de duplicación (doble en la medida en que sea necesario) para hacer primero una tabla de multiplicación parcial. Luego, dibuja un andamio y usa resta repetida para hacer cada división. Cuando hayas terminado, asegúrate de que el resto sea menor que el divisor. Entonces, revisa la respuesta. Todo el trabajo debe mostrarse en el espacio provisto. Después de verificar, escriba la respuesta en el espacio proporcionado al inicio del problema.
|
a.\(361 \div 53\) = _______________
|
|||
|
b.\(279 \div 37\) = _______________
|
|||
|
c.\(200 \div 24\) = ___________________
|
|||
|
d.\(887 \div 231\) = ______________
|
|||
|
e.\(415 \div 72\) = _______________
|
|||
|
f.\(1235 \div 214\) = _____________
|
|||
|
g.\(3128 \div 321\) = _____________
|
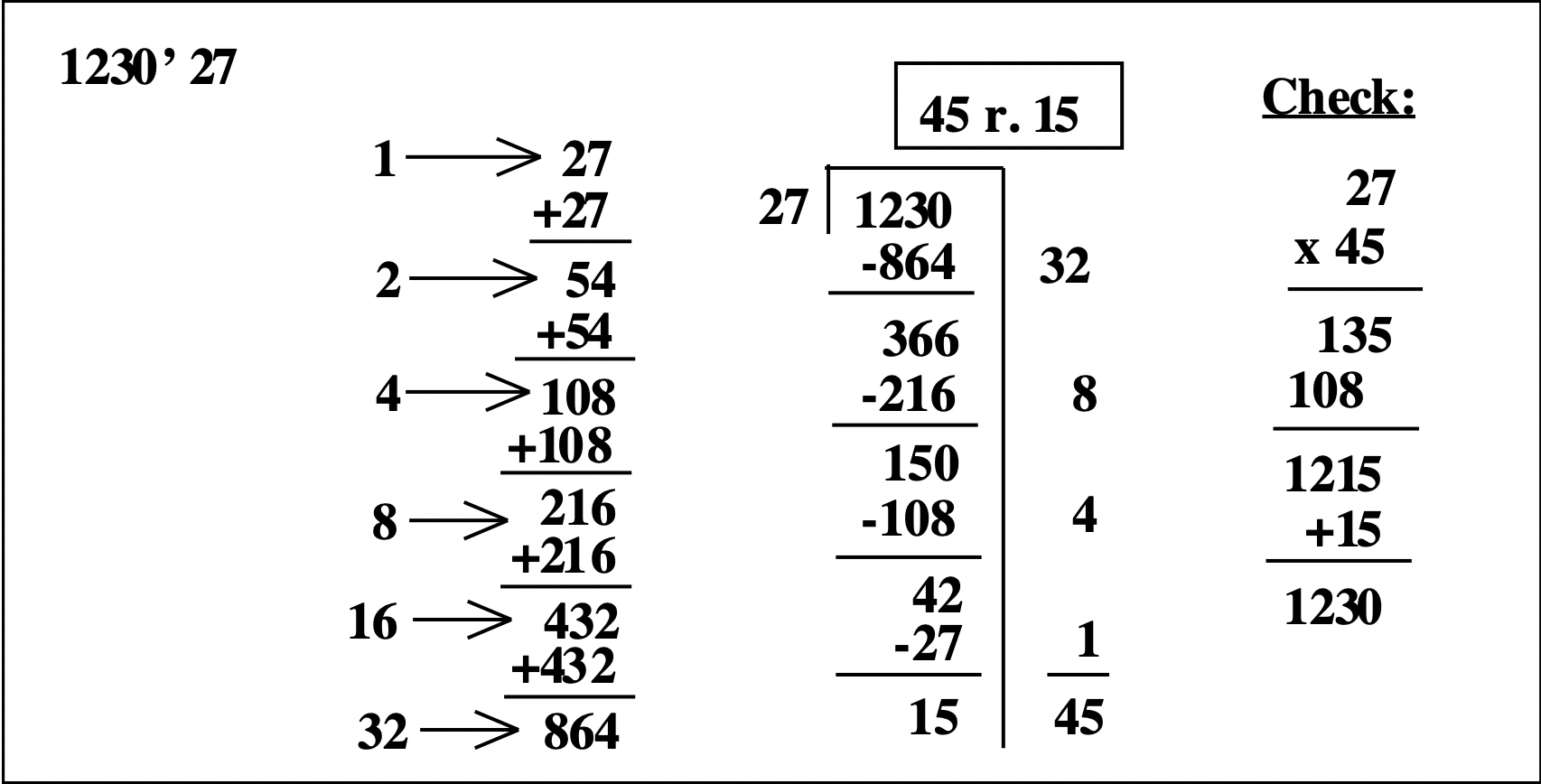
El siguiente es un ejemplo para mostrar que la duplicación puede continuar de esta manera. Se deja de duplicar si un doble más da un número mayor que el cociente. A continuación se muestra\(1230 \div 27\).
Agradezco y le doy crédito a mi hijo, Jakob, con este método de duplicar para averiguar más de ocho veces el divisor. Siempre había usado un método que empleaba el uso de valores posicionales y múltiplos de 10, a los que llegaremos después de hacer algunos de esta manera. Jakob, de nueve años y en cuarto grado, odiaba la división larga porque no tenía sentido para él, y tenía problemas con las “adivinanzas” involucradas. Antes era capaz de mostrarle mi método donde usas el método de duplicación para hacer una tabla de multiplicación parcial solo hasta 8 veces el divisor, hizo todos los problemas como la forma que se muestra arriba. Finalmente le dio sentido, ¡y los hizo todos correctamente!!! Me abrió una forma de pensar completamente nueva. ¡Los niños y los estudiantes pueden ser grandes innovadores! Es maravilloso cuando tienes la oportunidad de explorar y descubrir por tu cuenta, y encontrar tu propia solución que tenga sentido. Tenemos que recordar que no hay nada sagrado en ningún algoritmo para la división, ni en ninguna otra operación.
Bien, es hora de que pruebes algunos problemas más, usando el método de duplicación, donde el cociente es mayor que 10. El primer problema es exactamente el mismo que se hizo anteriormente. Si te quedas atascado, mira hacia atrás y copia como lo hice en otro trozo de papel. Entonces, inténtalo de nuevo.
Para cada problema de división (comenzando en la página siguiente), use el método de duplicación (doble en la medida en que sea necesario) para hacer una tabla de multiplicación parcial. Luego, dibuja un andamio y usa resta repetida para hacer cada división. Entonces, revisa la respuesta, y asegúrate de que el resto sea menor que el dividendo. Se debe mostrar todo el trabajo. Después de verificar, escriba la respuesta en el espacio proporcionado al inicio del problema.
Comprobar:\(\begin{aligned} 27 \\ \underline{\times 45} \\ 1215 \\ \underline{+ 15} \\ 1230 \end{aligned}\)
Se puede usar una calculadora para verificar la respuesta. Por ejemplo, para comprobar que 45 r. 15 es la respuesta correcta a\(1230 \div 27\), es necesario multiplicar 27 por 45 y sumar 15. La respuesta debe ser 1230. Puedes usar la calculadora para hacer la multiplicación y suma, pero anota los pasos.. Se vería de la manera en que se muestra a la derecha.
|
a.\(1230 \div 27\) = ______________
|
|||
|
b.\(603 \div 48\) = _______________
|
|||
|
c.\(1346 \div 41\) = ______________
|
|||
|
d.\(3512 \div 43\) = ______________
|
Es posible que hayas notado que la tabla de multiplicación parcial podría alargarse si tienes que seguir duplicando durante bastante tiempo. Además, no es tan fácil sumar los números a la derecha del andamio. Otro enfoque es aprovechar el hecho de que multiplicar un número entero por 10 o 100, etc., simplemente agrega ceros al final del número. Por ejemplo, si sabes 53 veces 2 es 106, entonces 53 veces 20 es 1060, y 53 veces 200 es 10600. Usaremos este hecho para dividir usando resta repetida cuando el cociente sea superior a 10.
Mira hacia atrás en el último problema que hiciste en el Ejercicio 2:\(3512 \div 43\). Tuviste que duplicar hasta que te diste cuenta de lo que era 64 veces 43. En el cuadro al final de esta página hay una manera diferente de hacer el mismo problema. La explicación y los pasos están en esta y en la página siguiente.
Paso 1: Usa la duplicación para componer una tabla de multiplicación parcial hasta 8 veces 43.
Paso 2: Dibuja el andamio.
Paso 3: Escanea 3512 comenzando con el dígito más a la izquierda hasta obtener un número mayor o igual a 43. Prueba 3, luego 35, luego 351. Tenga en cuenta cuántos dígitos más hay después de 351. En este caso sólo hay uno (el 2). Esto significa que puedes tomar un múltiplo de diez veces 43 a la vez. (En el antiguo algoritmo estándar, cuando adivina y pones el número por encima del 1 en 3512, lo estás poniendo en el valor posicional de las decenas). Entonces ponemos un cero debajo de los números extra en el dividendo (el 2) y el mismo número de ceros a la derecha del andamio. Deja un espacio para un dígito antes del 0 a la derecha del andamio.
Paso 4: Ahora, mira la tabla de multiplicación parcial para determinar el número más grande que puedes restar de 351. Es 344, que es 8 veces 43. Tenga en cuenta que si 8 veces 43 es 344, entonces 80 veces 43 es 3440. Ya has puesto el cero extra debajo del 2, así que solo pon el 344 frente al 0 que ya dejaste en el paso 3. Tenga en cuenta que 3440 es 80 veces 43, y debe realizar un seguimiento de eso a la derecha del andamio. Ya has escrito el cero abajo en el paso 3, así que simplemente pon un 8 delante de ese 0. Acabas de restar ochenta 43's del dividendo, ya que 80 veces 43 es 3440. Restar 3440 de 3512 para obtener 72.
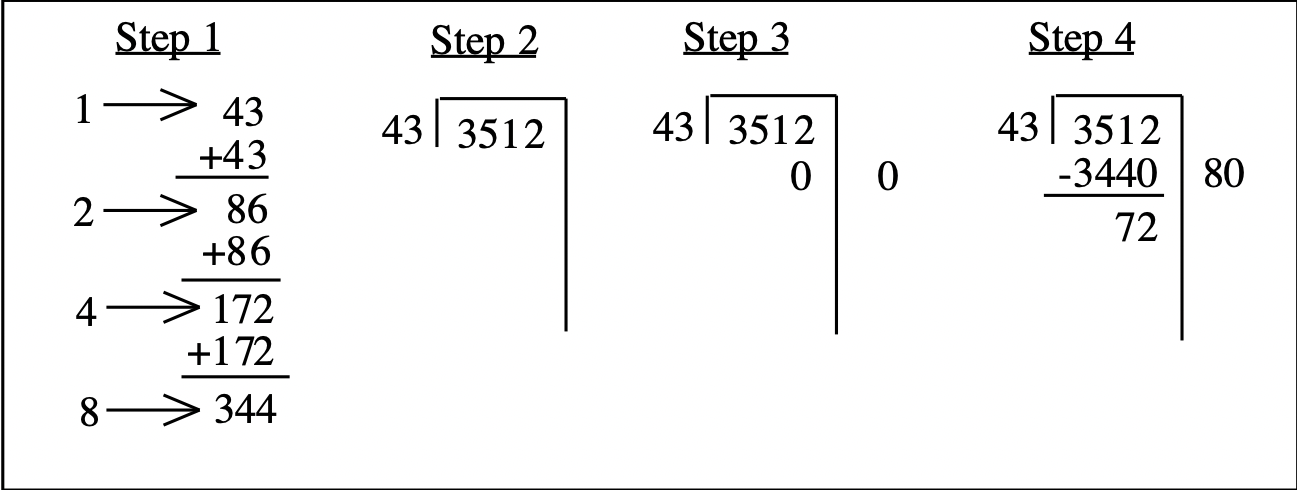
Paso 5: Ahora tenemos que ver cuántos 43 más se pueden restar de 72. No hay ceros adicionales para virar en este momento, como en el paso 4. Podemos restar 1 43 más de 72, así que escribe un 1 a la derecha del andamio, y restar 43 de 72 para obtener 29.
Pasos 6, 7 y 8: Ya que 29 es menor que 43, ese es el resto, así que suma los números a la derecha del andamio para obtener el cociente.Escribe la respuesta como cociente y resto en una caja arriba del problema. Consulta la respuesta. Se puede usar una calculadora para multiplicar 81 por 43, que es 3483, y luego agregar 29.
A continuación se muestran los últimos cuatro pasos.
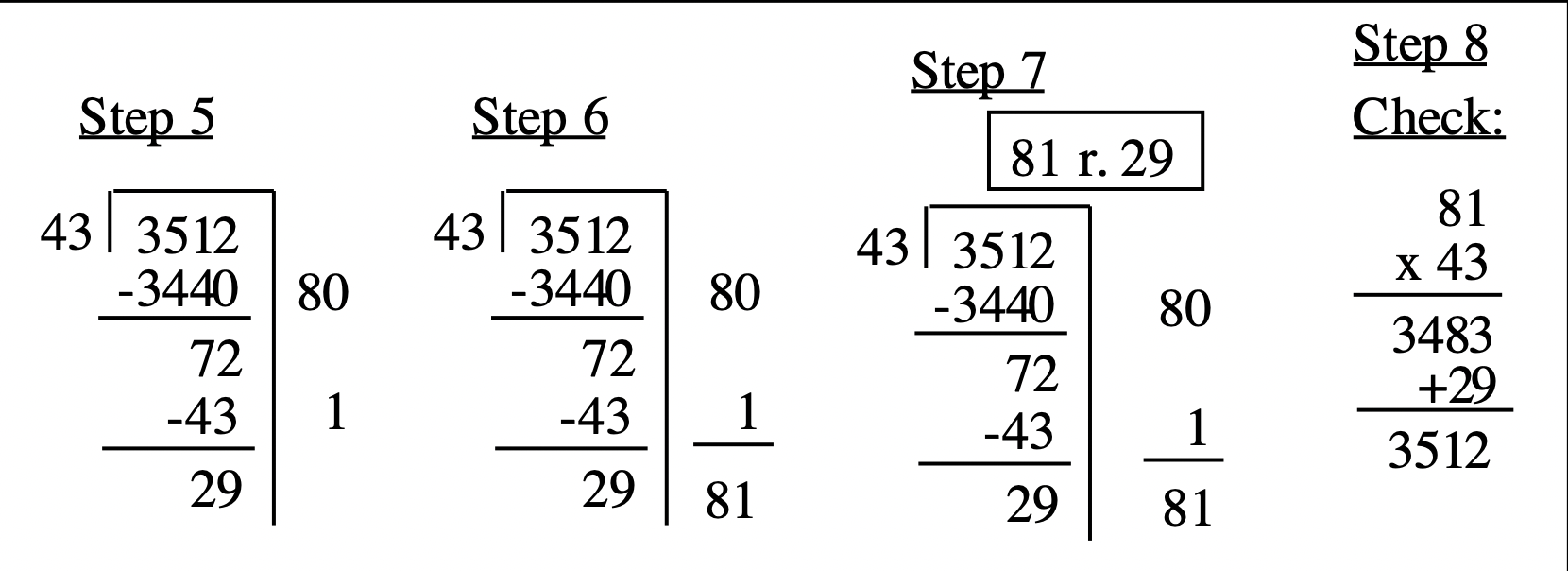
Si tuvieras que mostrar tu trabajo, así es como se vería todo el problema:
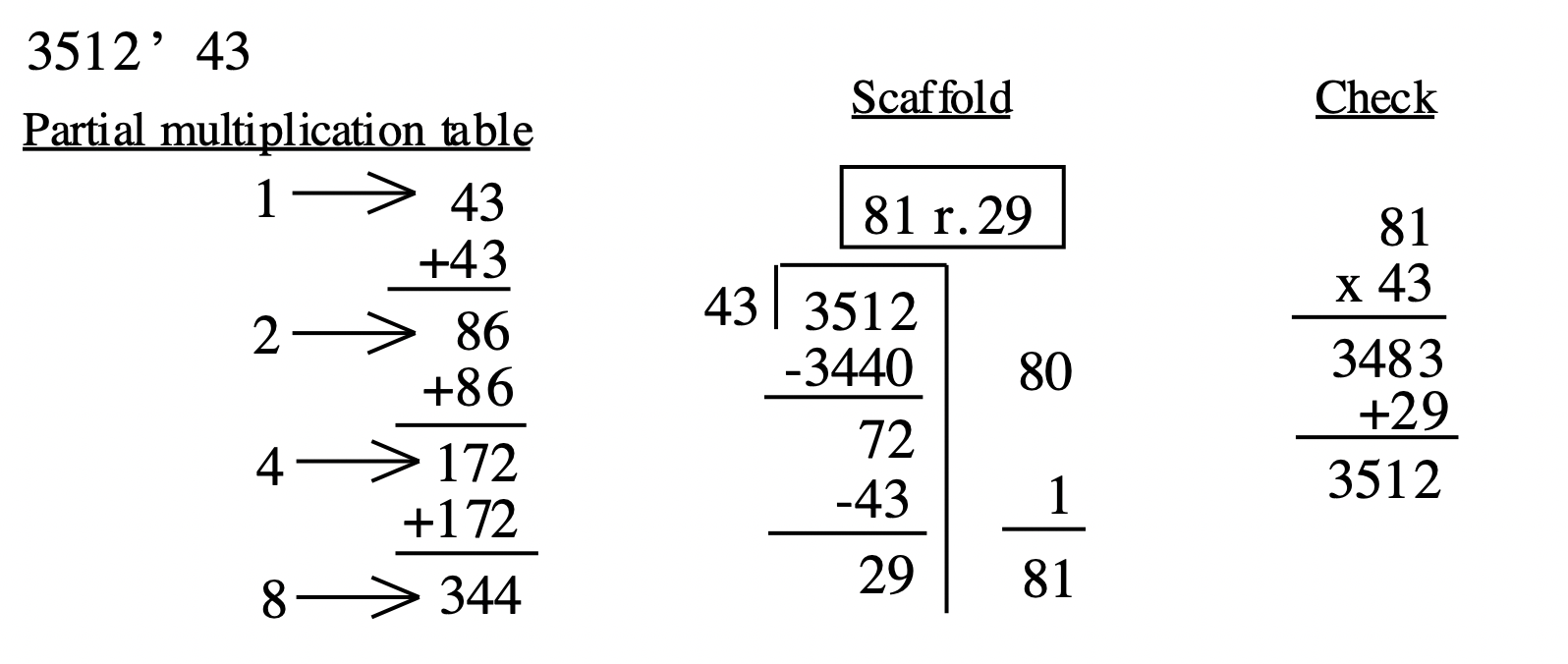
Así es como se vería hacerlo de la manera en que lo hiciste en el ejercicio 2:
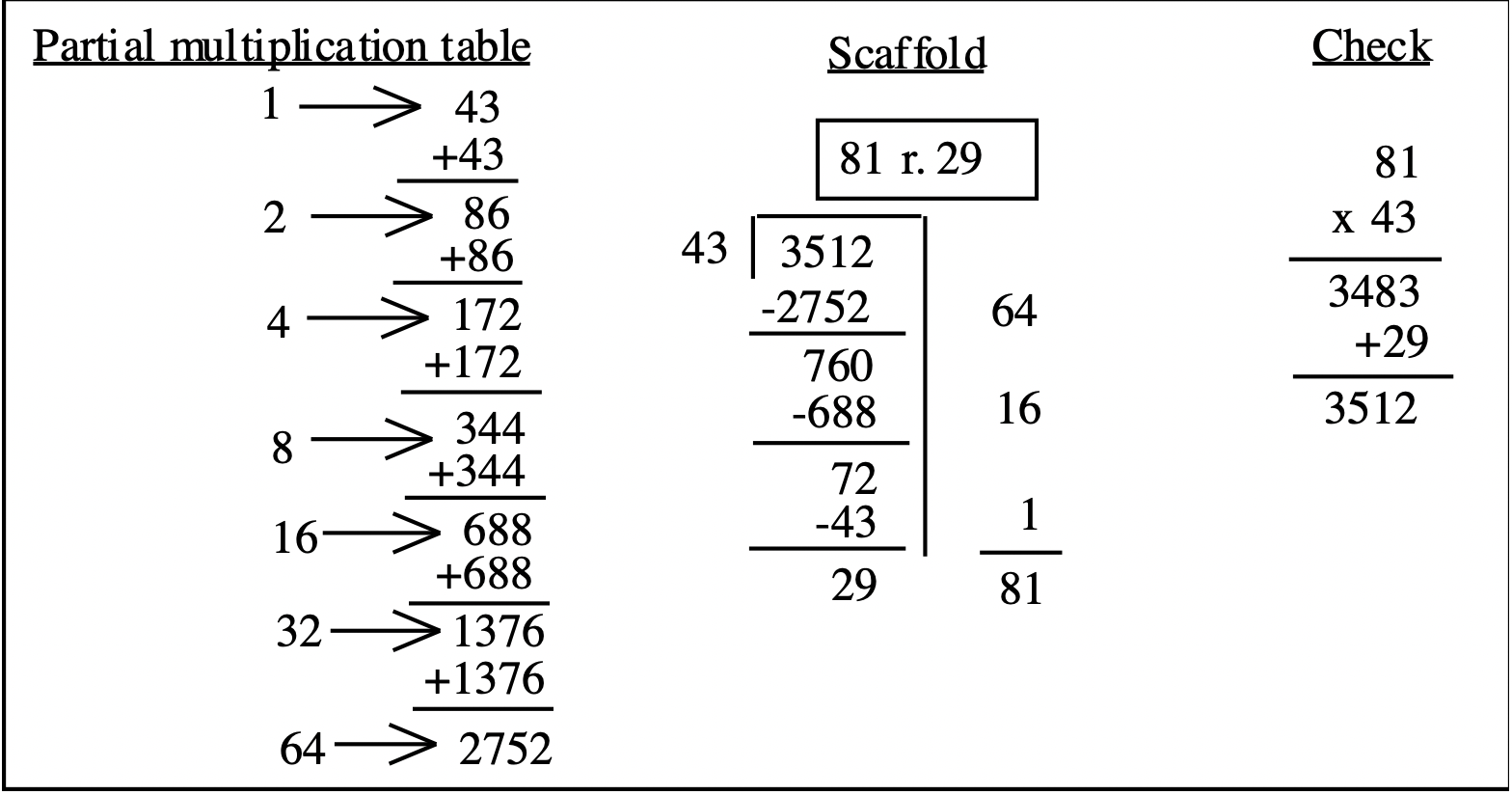
Para ambos métodos, cuando añades los números a la derecha del andamio para obtener el cociente, ¡ten cuidado de alinear los valores posicionales! Ambos métodos producen el mismo resultado y funcionan igual de bien. ¡Lo importante es que el procedimiento tenga sentido para ti!
A continuación se muestran dos ejemplos más usando múltiplos de decenas (poniendo los ceros adicionales).
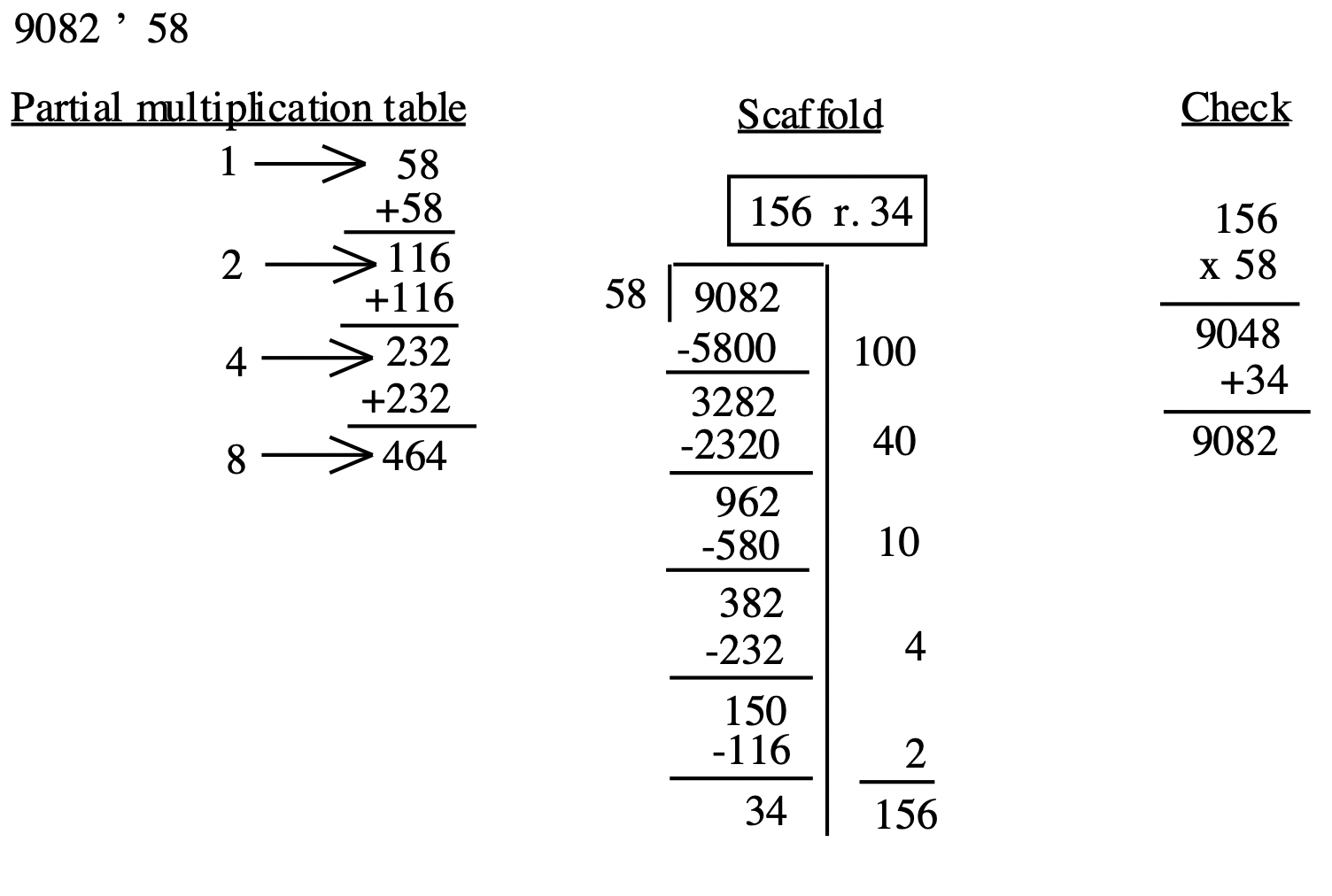
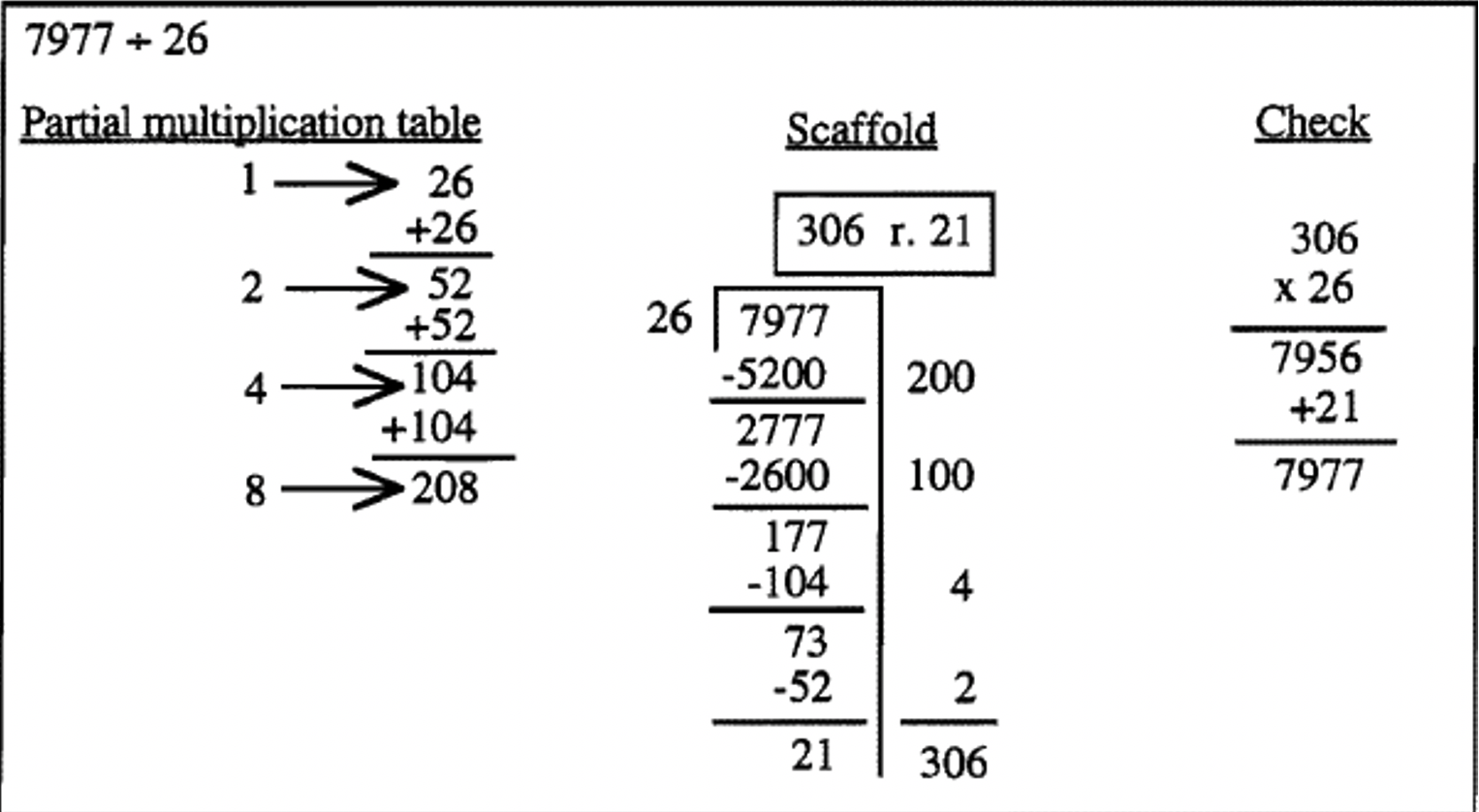
En el ejemplo anterior, muchas personas (niños y adultos) extrañan escribir el cero en el lugar de las decenas para la respuesta de 306 cuando lo hacen de la forma de división corta que suele enseñarse. Una respuesta muy común a este problema es 36 r. 21. En el primer paso anterior, escribir el número completo en el costado realmente enfatiza el hecho de que no solo estás multiplicando 26 por un 2 para obtener 52 estás multiplicando 26 por 200 para obtener 5200. Sabes que la respuesta al problema será de más de 200 ya que ya restaste 200 26's del 7977. Cuando te quedan 177, simplemente notas solo puedes restar unos cuantos 26's más Si uno escribe pulcramente los números de la derecha, no hay números en el lugar de las decenas para sumar. ¡Ni siquiera surge la confusión sobre el cero!
Para cada problema de división, haga una tabla de multiplicación parcial hasta 8 veces el divisor. Luego, dibuja un andamio y usa resta repetida para hacer cada división. Use múltiplos de decenas (poniendo ceros adicionales cuando sea necesario) para hacer estos problemas. Entonces, revisa la respuesta. Todo el trabajo debe mostrarse en el espacio provisto. Después de verificar, escriba la respuesta en el espacio proporcionado al inicio del problema. Se puede usar una calculadora para verificar la respuesta, pero anote los pasos.
|
a.\(1230 \div 27\) = ______________
|
|||
|
b.\(603 \div 48\) = _______________
|
|||
|
c.\(1346 \div 41\) = ______________
|
|||
|
d.\(3512 \div 43\) = ______________
|
|||
|
e.\(66289 \div 325\) = ____________
|
|||
|
f.\(5222 \div 21\) = ______________
|
Hacer la tabla de multiplicación parcial en el lateral, en conjunto con el método de resta repetida, es completamente opcional. Pero, si primero inventas la mesa, no necesitas hacer ninguna multiplicación o estimación en tu cabeza. Otra opción es omitir hacer la tabla de multiplicación parcial por completo y seguir usando el método de resta repetida. En este caso, si no estás seguro de cuántas veces se puede restar el divisor, subestima en cada paso que no estás absolutamente seguro de cuántas veces del divisor restar. En otras palabras, asegúrate de no multiplicar algo por el divisor y salir con un número demasiado grande para restar del dividendo. Subestimar está bien con el método de resta repetida porque solo restas un poco más en el siguiente paso. Por ejemplo, en el ejemplo anterior, podrías haber restado 200 26's (5200) en el primer paso y luego 100 26 más en el segundo paso, o podrías haber restado 300 26's en el primer paso multiplicando 26 por 3 en tu cabeza si estuvieras seguro de que 26 veces 3 no era demasiado grande. Me gusta la tabla de multiplicación parcial porque quita las conjeturas del problema. En el ejemplo en el cuadro de abajo, la división se realiza usando resta repetida sin componer una tabla En cambio, se estima cuántos de los divisor se pueden restar en cada paso. En este caso, la multiplicación debe hacerse en tu cabeza, o en el costado, a medida que avanzas.
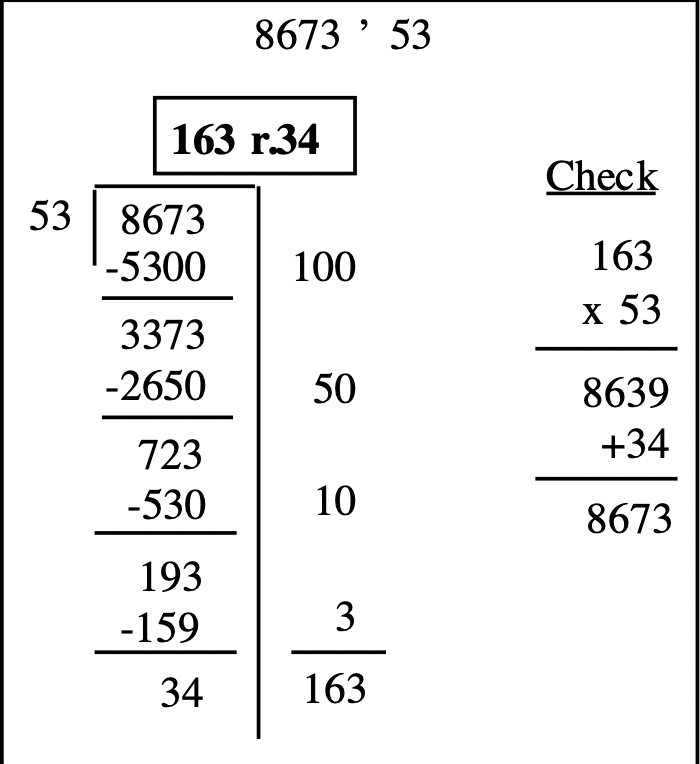
Aquí hay una manera de dividir\(8673 \div 53\) sin el habitual trabajo de preparación de componer primero una tabla de multiplicación parcial. Esto significa que la multiplicación debe hacerse en el camino. Es importante tener en cuenta que está bien subestimar cuando se usa el método de resta repetida (a diferencia del método de división tradicional), porque siempre se puede restar más en el siguiente paso. Por otro lado, sobreestimar hará que vuelvas atrás y rehagas el problema. Primero observo que 53 entra en 86 una vez, así que resto 100 53's, o 5300, de 8673. A continuación, estimación\(337 \div 53\). Ya que no estoy seguro si es 5 o 6 veces, juego a lo seguro y por lo tanto, estimo 5. Entonces, resto 50 veces 53, o 2650, de 3373. (Nota tengo que hacer la multiplicación en mi cabeza.) Bueno, veo otro 53 se puede restar de 72, así que resto 10 veces 53, o 530, de 723. Entonces, estimo 53 entra en 193 al menos 3 veces, así que resto 3 veces 53 de 193. Dado que 34 es menor que 53, 34 es el resto. Suma los números en el costado para obtener el cociente de 163. Verifica multiplicando\(53 \times 163\) y sumando el resto de 34 para obtener 8673.
En el algoritmo de división tradicional, no hay margen para subestimar o sobreestimar. Tienes que volver atrás y borrar si pones el dígito equivocado en un valor posicional determinado. Si estimas incorrectamente, la multiplicación que haces termina siendo una pérdida de tiempo y esfuerzo, y tienes que empezar de nuevo. Además, la mayoría de la gente no piensa en qué o por qué están poniendo dígitos en un lugar en particular. No piensan en los valores posicionales, o esa división es realmente sobre la resta repetida. Creo que el método del andamio, con o sin constituir una tabla de multiplicación parcial, promueve una mejor comprensión de la división, y es menos estresante que el método tradicional de “adivinar” donde no hay absolutamente margen de error. La única ventaja del algoritmo tradicional es que es un atajo al método del andamio, y utiliza menos espacio en papel.
Al final, realmente le toca al individuo que hace la división decidir de qué manera hacerlo.
Aquí hay un ejemplo de división\(27984 \div 37\) usando el método de duplicación.
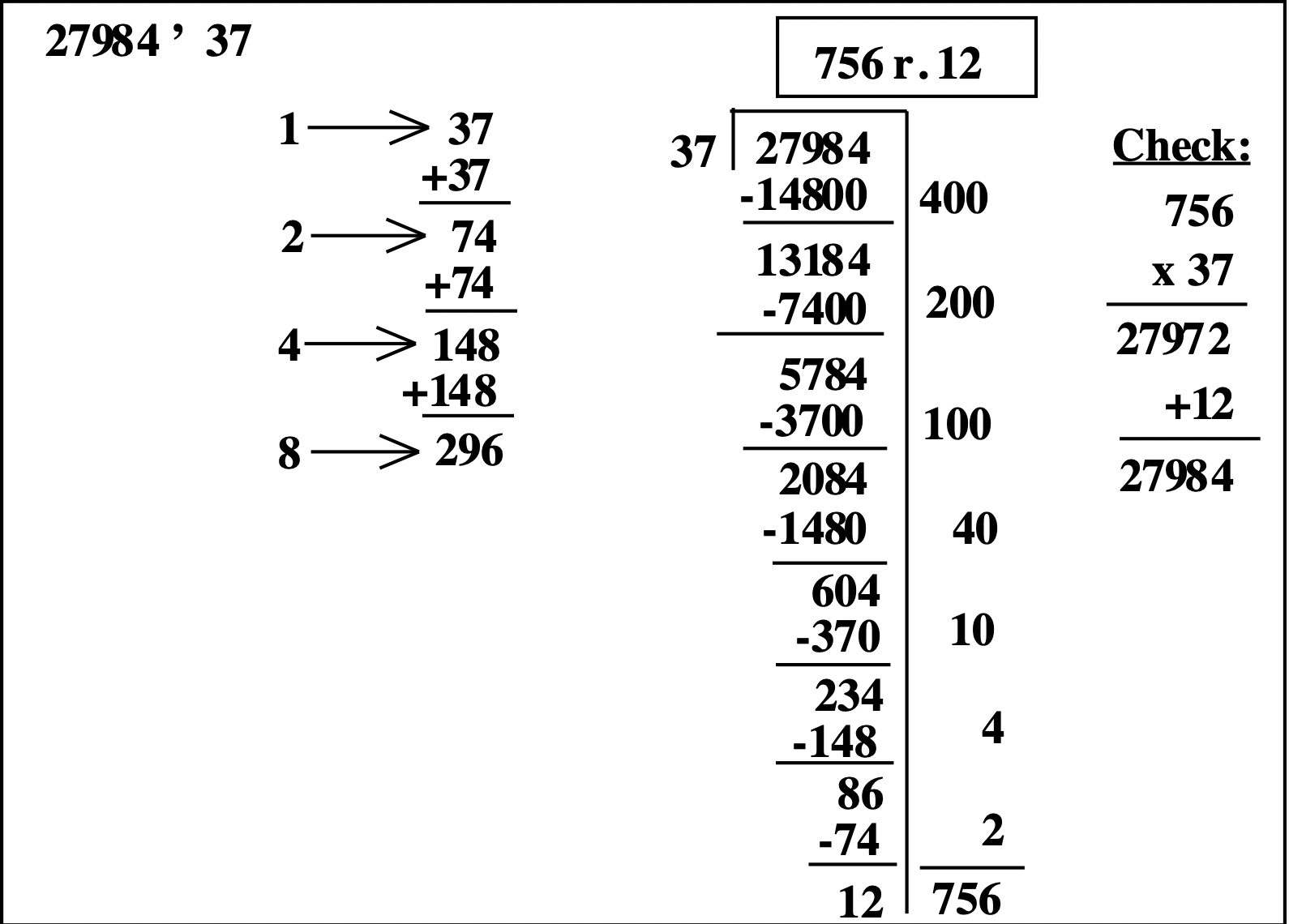
Al componer una tabla de multiplicar, no tiene que ser parcial. En base diez, duplicar para obtener el divisor por 1, 2, 4 u 8 nos da estimaciones lo suficientemente cercanas la mayor parte del tiempo. El peor caso posible es que 7 es el número correcto de veces que se puede restar algo, como en el ejemplo anterior. En ese caso, primero restaríamos 4, luego 2, luego 1. Eso no sucede con demasiada frecuencia, pero de vez en cuando sí. Otra estrategia es agregar una adición más a la tabla parcial para que también sepas qué 6 veces es el divisor. Para ello, después de calcular qué es 4 veces el divisor, agrega 2 más, como se muestra a continuación (agrega 74 en lugar de duplicar 148), luego agrega 2 más nuevamente (agrega 74 nuevamente) para obtener 8 veces el número. Mira la diferencia.
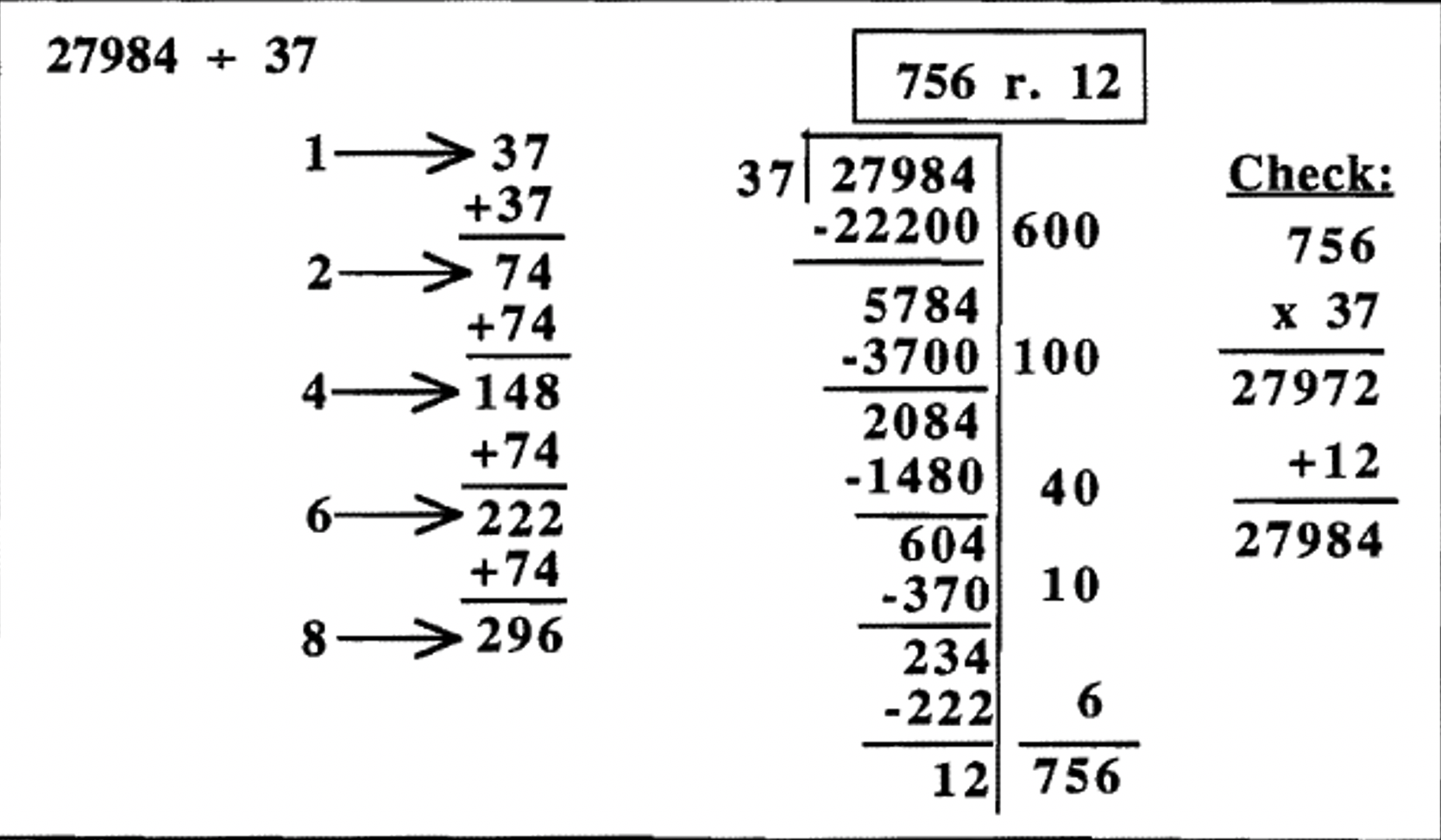
De hecho, podríamos haber utilizado la adición repetida para averiguar las respuestas al divisor que se multiplican por cada dígito del 1 al 9, en cuyo caso nunca ocurriría subestimar ni sobreestimar. Aunque esto no deja absolutamente ninguna conjetura en absoluto, es más trabajo del necesario en la mayoría de los casos. Aquí hay un ejemplo de cómo alguien podría hacer el mismo problema hecho en la página anterior haciendo primero una tabla de multiplicación completa. Es fácil hacer la división si haces esto primero, pero hay mucho trabajo de preparación al principio para hacer la mesa.
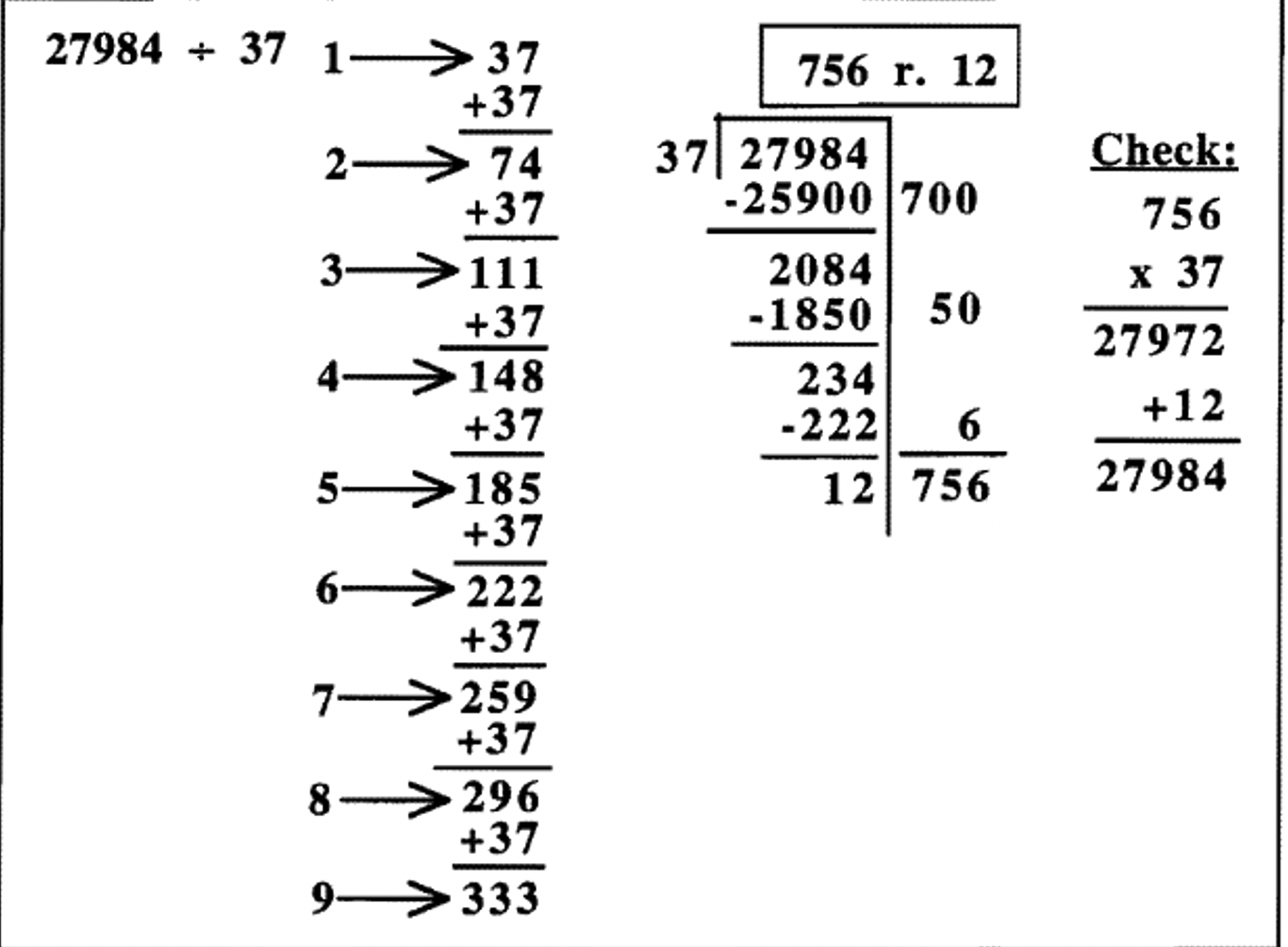
Mira hacia atrás en las tres formas diferentes en que\(27984 \div 37\) se hizo la división. La primera forma, mostrada en la página anterior, tenía una breve tabla de multiplicación parcial (sólo tres adiciones para el trabajo de preparación), pero el método de resta repetida tardó un poco más. Se requirieron siete restas para obtener la respuesta (mira a la derecha del andamio), porque el 700 dio tres pasos 400, 200, 100; el 50 dio dos pasos 40 y 10; y el 6 dio dos pasos 4 y 6. El segundo camino tuvo una suma más para la preparación de la tabla de multiplicación, y luego solo requirió cinco restas para obtener la respuesta (mira a la derecha del andamio), porque el 700 dio dos pasos 600, y 100; el 50 dio dos pasos 40 y 10; y el 6 dio un paso. La tercera vía, mostrada en la parte superior, requirió ocho adiciones de trabajo de preparación para hacer la tabla de multiplicar, pero la división fue muy sencilla, dando sólo tres pasos. Si lo haces de esta manera, también puedes escribir el 756 arriba en la parte superior, como lo haces cuando lo haces usando el algoritmo tradicional porque nunca puedes subestimar o sobreestimar.
Dependiendo del problema en particular, un método puede ser más rápido que otro, pero muchas veces no lo sabrías hasta que hayas completado el problema. Normalmente solo hago la duplicación a 8 para obtener estimaciones lo suficientemente buenas, pero si quieres hacer una tabla más completa, funciona igual de bien. Tienes que decidir si prefieres hacer más trabajo de preparación por adelantado para posiblemente hacer que la división sea más rápida.


