15.5: Secuencias Recursivas Complejas

Última actualización
Guardar como PDF

Page ID: 110502

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Ahora exploraremos secuencias definidas recursivamente de números complejos.

Secuencia Recursiva

Una relación recursiva es una fórmula que relaciona el siguiente valor,$z_{n+1},$ en una secuencia con el valor anterior,$z_{n} .$ Además de la fórmula, necesitamos un valor inicial,$z_{0}$.

La secuencia de valores producida es la secuencia recursiva.

Ejemplo 15

Dada la relación recursiva$z_{n+1}=z_{n}+2, \quad z_{0}=4,$ generar varios términos de la secuencia
recursiva.

Solución

Se nos da el valor inicial,$z_{0}=4 .$ La fórmula recursiva sostiene para cualquier valor de$n,$ así que
si$n=0,$ entonces nos$z_{n+1}=z_{n}+2$ diría$z_{0+1}=z_{0}+2,$ o más simplemente,$z_{1}=z_{0}+2$

Observe esto define$z_{1}$ en términos de$z_{0},$ lo conocido para que podamos calcular el valor:
$ z_{1}=z_{0}+2=4+2=6 $

Ahora dejando que$n=1,$ la fórmula nos diga$z_{1+1}=z_{1}+2,$ o$z_{2}=z_{1}+2 .$ Nuevamente, la fórmula da el siguiente valor en la secuencia en términos del valor anterior.

(z_ {2} =z_ {1} +2=6+2 = 8\)

Continuando,

$z_{3}=z_{2}+2=8+2=10$

$z_{4}=z_{3}+2=10+2=12$

El ejemplo anterior generó una secuencia lineal básica de números reales. El mismo proceso se puede utilizar con números complejos.

Ejemplo 16

Dada la relación recursiva$z_{n+1}=z_{n} \cdot i+(1-i), \quad z_{0}=4,$ generar varios términos de la secuencia
recursiva.

Solución

Se nos da$z_{0}=4 .$ Usando la fórmula recursiva:

$z_{1}=z_{0} \cdot i+(1-i)=4 \cdot i+(1-i)=1+3 i$

$z_{2}=z_{1} \cdot i+(1-i)=(1+3 i) \cdot i+(1-i)=i+3 i^{2}+(1-i)=i-3+(1-i)=-2$

$z_{3}=z_{2} \cdot i+(1-i)=(-2) \cdot i+(1-i)=-2 i+(1-i)=1-3 i$

$z_{4}=z_{3} \cdot i+(1-i)=(1-3 i) \cdot i+(1-i)=i-3 i^{2}+(1-i)=i+3+(1-i)=4$

$z_{5}=z_{4} \cdot i+(1-i)=4 \cdot i+(1-i)=1+3 i$

Observe que esta secuencia está exhibiendo un patrón interesante —empezó a repetirse.

Conjunto Mandelbrot

El Conjunto Mandelbrot es un conjunto de números definidos en base a secuencias recursivas

Conjunto Mandelbrot

Para cualquier número complejo$c,$ definir la secuencia$z_{n+1}=z_{n}^{2}+c, \quad z_{0}=0$

Si esta secuencia siempre permanece cerca del origen (dentro de 2 unidades), entonces el número$c$ es parte del Conjunto Mandelbrot. Si la secuencia se aleja del origen, entonces el número$c$ no forma parte del conjunto.

Ejemplo 17

$c=1+i$Determine si forma parte del conjunto Mandelbrot.

Solución

Empezamos con$z_{0}=0$. Seguimos omitiendo algún detalle de los cálculos

$z_{1}=z_{0}^{2}+1+i=0+1+i=1+i$

$z_{2}=z_{1}^{2}+1+i=(1+i)^{2}+1+i=1+3 i$

$z_{3}=z_{2}^{2}+1+i=(1+3 i)^{2}+1+i=-7+7 i$

$z_{4}=z_{3}^{2}+1+i=(-7+7 i)^{2}+1+i=1-97 i$

Ya podemos ver que estos valores se están volviendo bastante grandes. No parece que$c=1+i$ forme parte del conjunto de Mandelbrot.

Ejemplo 18

$c=0.5 i$Determine si forma parte del conjunto Mandelbrot.

Solución

Empezamos con$z_{0}=0$. Seguimos omitiendo algún detalle de los cálculos

$z_{1}=z_{0}^{2}+0.5 i=0+0.5 i=0.5 i$

$z_{2}=z_{1}^{2}+0.5 i=(0.5 i)^{2}+0.5 i=-0.25+0.5 i$

$z_{3}=z_{2}^{2}+0.5 i=(-0.25+0.5 i)^{2}+0.5 i=-0.1875+0.25 i$

$z_{4}=z_{3}^{2}+0.5 i=(-0.1875+0.25 i)^{2}+0.5 i=-0.02734+0.40625 i$

Si bien no es definitivo con estas pocas iteraciones, sí parece que este valor sigue siendo pequeño, lo que sugiere que$0.5 i$ es parte del conjunto de Mandelbrot.

Pruébalo ahora 5

$c=0.4+0.3 i$Determine si forma parte del conjunto Mandelbrot.

Responder

$z_{1}=z_{0}^{2}+0.4+0.3 i=0+0.4+0.3 i=0.4+0.3 i$

$z_{2}=z_{1}^{2}+0.4+0.3 i=(0.4+0.3 i)^{2}+0.4+0.3 i = 0.47+0.54 i$

$z_{3}=z_{2}^{2}+0.5 i=(-0.25+0.5 i)^{2}+0.5 i=-0.1875+0.25 i$

$z_{4}=z_{3}^{2}+0.5 i=(-0.1875+0.25 i)^{2}+0.5 i=-0.02734+0.40625 i$

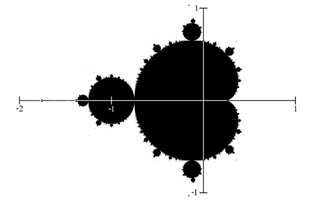$clipboard_ed4d262f8e62c4ae64b87e18c256770bc.png$ Si se prueban todos los números complejos, y trazamos cada número que está en el conjunto de Mandelbrot en el plano complejo, obtenemos la forma a la derecha [1].

El límite de esta forma exhibe cuasi-auto-similitud, en que las porciones se ven muy similares al conjunto.

Además de colorear el conjunto de Mandelbrot en negro, es común al color los puntos en el plano complejo que rodea al conjunto. Para crear una coloración significativa, a menudo las personas cuentan el número de iteraciones de la secuencia recursiva que se requieren para que un punto se aleje más de 2 unidades del origen. Por ejemplo, usando$c=1+i$ lo anterior, la secuencia estaba a la distancia 2 del origen después de sólo dos recursiones.

Para algunos otros números, puede tomar decenas o cientos de iteraciones para que la secuencia se aleje del origen. Los números que se hacen grandes rápidamente son coloreados de un tono, mientras que los colores que son lentos para crecer son coloreados de otro tono. Por ejemplo, en la imagen de abajo [2], el azul claro se utiliza para los números que se agrandan rápidamente, mientras que los tonos más oscuros se utilizan para los números que crecen más lentamente. Verdes, rojos y morados se pueden ver cuando acercamos el zoom, esos se utilizan para números que crecen muy lentamente.

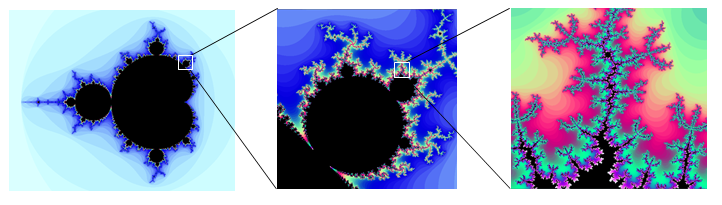
$clipboard_effebf3c2326419d73ecdad66e1b38474.png$

El conjunto Mandelbrot, por tener una definición tan simple, exhibe una inmensa complejidad. Acercar otras partes del conjunto produce fascinantes formas arremolinadas.

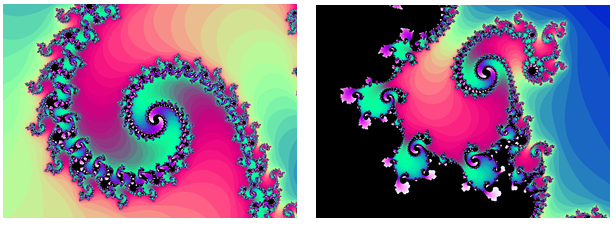
$clipboard_ef04205ce7af9e8e310324e0282465045.png$

[1] es.wikipedia.org/wiki/Archivo:Mandelset_Hires.png

[2] Esta serie se generó usando el Explorador de Conjuntos Mandelbrot de Scott