15.4: Números complejos

Última actualización
Guardar como PDF

Page ID: 110513

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Los números con los que está más familiarizado se llaman números reales. Estos incluyen números como 4, 275, -200, 10.7, ½, π, y así sucesivamente. Todos estos números reales se pueden trazar en una recta numérica. Por ejemplo, si quisiéramos mostrar el número 3, trazamos un punto:

$clipboard_ed293781d1b34e01063905160d3a6692c.png$

Para resolver ciertos problemas como$x^{2}=-4$, se hizo necesario introducir números imaginarios.

Número imaginario$i$

El número imaginario$i$ se define como$i=\sqrt{-1}$.

Cualquier múltiplo real de$i$, como$5i$, también es un número imaginario.

Ejemplo 6

Simplificar$\sqrt{-9}$.

Solución

Podemos separar$\sqrt{-9}$ como$\sqrt{9} \sqrt{-1} .$ Podemos tomar la raíz cuadrada de$9,$ y escribir la raíz cuadrada de -1 como$i$

\[\sqrt{-9}=\sqrt{9} \sqrt{-1}=3 i \nonumber \]

Número complejo

Un número complejo es un número$z=a+b i,$ donde$a$ y$b$ son números reales

$a$es la parte real del número complejo
$b$es la parte imaginaria del número complejo

Para trazar un número complejo como$3-4 i$, necesitamos algo más que una línea numérica ya que hay dos componentes al número. Para trazar este número, necesitamos dos líneas numéricas, cruzadas para formar un plano complejo.

Plano complejo

En el plano complejo, el eje horizontal es el eje real y el eje vertical es el eje imaginario.

Ejemplo 7

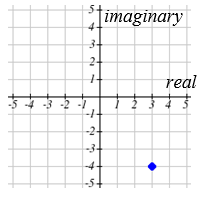
Trazar el número$3-4 i$ en el plano complejo.

Solución

La parte real de este número es 3, y la parte imaginaria es -4. Para trazar esto, dibujamos un punto 3 unidades a la derecha del origen en dirección horizontal y 4 unidades hacia abajo en dirección vertical.

Debido a que esto es análogo al sistema de coordenadas cartesianas para trazar puntos, podemos pensar en trazar nuestro número complejo$z=a+b i$ como si estuviéramos trazando el punto$(a, b)$ en coordenadas cartesianas. A veces la gente escribe números complejos como$z=x+y i$ para resaltar esta relación.

Aritmética en números complejos

Antes de sumergirnos en los usos más complicados de los números complejos, asegurémonos de recordar la aritmética básica involucrada. Para sumar o restar números complejos, simplemente sumamos los términos similares, combinando las partes reales y combinando las partes imaginarias.

Ejemplo 8

Agregar$3-4 i$ y$2+5 i$.

Solución

Añadiendo$(3-4 i)+(2+5 i),$ agregamos las partes reales y las partes imaginarias

$3+2-4 i+5 i$

$5+i$

Pruébalo ahora 3

Restar$2+5 i$ de$3-4 i$.

Contestar: $(3-4 i)-(2+5 i)=1-9 i$

Cuando sumamos números complejos, podemos visualizar la suma como un desplazamiento, o traslación, de un punto en el plano complejo.

Ejemplo 9

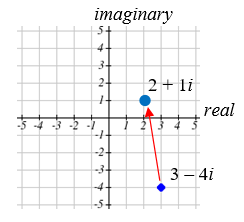
Visualice la adición$3-4 i$ y$-1+5 i$.

Solución

El punto inicial es$3-4 i$. Cuando agregamos$-1+3 i$, agregamos -1 a la parte real, moviendo el punto 1 unidades hacia la izquierda, y agregamos 5 a la parte imaginaria, moviendo el punto 5 unidades verticalmente. Esto desplaza el punto$3-4 i$ a$2+1 i$.

$clipboard_ea6efdc972c75055b1d2be426a4f8288b.png$

También podemos multiplicar números complejos por un número real, o multiplicar dos números complejos.

Ejemplo 10

Multiplicar:$4(2+5 i)$

Solución

Para multiplicar el número complejo por un número real, simplemente distribuimos como lo haríamos al multiplicar polinomios.

$\begin{array}{ll} 4(2+5 i) & \text{Distribute} \\ =4 \cdot 2+4 \cdot 5 i & \text{Simplify} \\ =8+20 i \end{array}$

Ejemplo 11

Multiplicar:$(2+5 i)(4+i)$

Solución

Para multiplicar el número complejo por un número complejo, simplemente distribuimos como lo haríamos al multiplicar polinomios.

$\begin{array}{ll} (2+5 i)(4+i) & \text{Expand} \\ =8+20 i+2 i+5 i^{2} & \text{Since }i=\sqrt{-1}, i^{2}=-1 \\ =8+20 i+2 i+5(-1) & \text{Simplify} \\ =3+22 i \end{array}$

Pruébalo ahora 4

Multiplicar$3-4 i$ y$2+3 i$.

Contestar: Multiplicar$(3-4 i)(2+3 i)=6+9 i-8 i-12 i^{2}=6+i-12(-1)=18+i$

Para entender visualmente el efecto de la multiplicación, exploraremos tres ejemplos.

Ejemplo 12

$clipboard_e05af910952ed538cabe1da2582f4c5a0.png$ Visualizar el producto$2(1+2 i)$

Solución

Multiplicando obtendríamos

$2 \cdot 1+2 \cdot 2 i = 2+4 i$

Observe que tanto las partes reales como las imaginarias han sido escaladas por 2. Visualmente, esto estirará el punto hacia afuera, lejos del origen.

Ejemplo 13

$clipboard_efde6c9009b12e2831a12499a39aaead0.png$ Visualizar el producto$i(1+2 i)$

Solución

Multiplicando, obtendríamos

$i \cdot 1+i \cdot 2 i = i+2 i^{2}=i+2(-1)=-2+i$

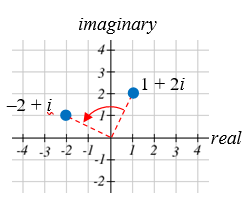
En este caso, la distancia desde el origen no ha cambiado, sino que el punto se ha girado alrededor del origen, 90° en sentido antihorario.

Ejemplo 14

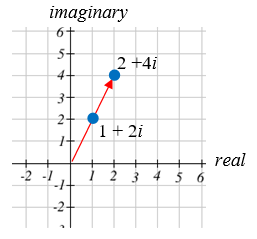
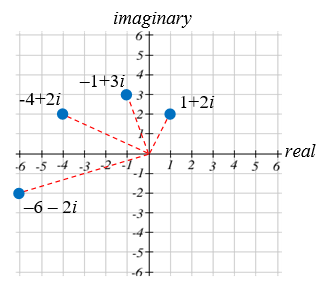$clipboard_e6bb92194b3f05d9193a2b2c8d15a95eb.png$ Visualizar el resultado de multiplicar$1+2 i$ por$1+i .$ Luego mostrar el resultado de multiplicar por$1+i$ otra vez.

Solución

Multiplicando$1+2 i$ por$1+i$,

$(1+2 i)(1+i)=1+i+2 i+2 i^{2}=1+3 i+2(-1)=-1+3 i$

Multiplicando por$1+i$ otra vez,

$(-1+3 i)(1+i) =-1-i+3 i+3 i^{2} =-1+2 i+3(-1) =-4+2 i$

Si$1+i$ volviéramos a multiplicar por, obtendríamos$–6–2i$. Al trazar estos números en el plano complejo, puede notar que cada punto se aleja tanto del origen, como gira en sentido antihorario, en este caso 45°.

En general, la multiplicación por un número complejo puede pensarse como una escala, cambiando la distancia desde el origen, combinada con una rotación alrededor del origen.