9.1: Fundamentos de Interés Compuesto

Última actualización
Guardar como PDF

Page ID: 110873

Jean-Paul Olivier
Red River College of Applied Arts, Science, & Technology

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Hace cinco años empezaste un GIC a largo plazo. El extracto bancario muestra que originalmente colocaste $15,000 en la cuenta ganando 5.95% en intereses compuestos anuales. Ahora tienes $20,026.09. En el primer año del GIC, ganaste 892.50 dólares en intereses. Los años posteriores obtuvieron intereses anuales de 945.60 dólares, $1,001.87, $1,061.48 y finalmente $1,124.64. Por supuesto, te gusta que el monto de los intereses aumentara cada año a pesar de que no hiciste más depósitos al GIC, pero ¿por qué sucedió esto?

El concepto de composición

Interés simple, interés compuesto: ¿cuál es la gran diferencia? Como puede ver en la siguiente figura, los cálculos de interés simples y compuestos comparten los mismos fundamentos de tiempo, tasa de interés y colocación de intereses en la cuenta. Pero la acumulación no es lo mismo, y con el tiempo el crecimiento del interés compuesto superará con creces al del interés simple.

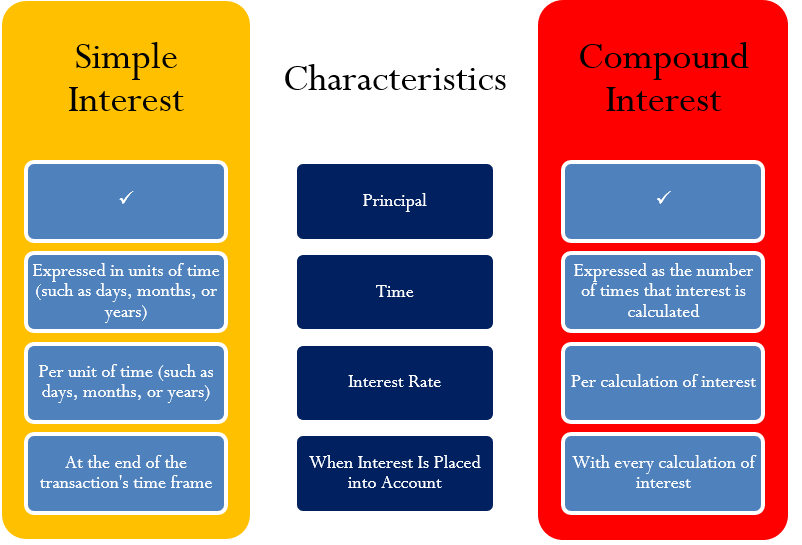
$clipboard_e57f2948544df00dee7f7c5caf9f08601.png$

En ambas formas de interés, el principal es el monto inicial que acumula intereses por un período de tiempo a una tasa de interés determinada. Pero se calcula el interés simple en proporción directa al monto inicial, la tasa de interés y el período de tiempo, mientras que el cálculo para el interés compuesto es, bueno, ¡no tan simple!

La diferencia crítica es la colocación de intereses en la cuenta. Bajo interés simple, convierte el interés en principal al final del período de tiempo de la transacción. Por ejemplo, en un GIC de interés simple de seis meses el saldo en su cuenta en cualquier momento anterior a la fecha de vencimiento es el principal original y nada más. Sólo al vencimiento aparece el interés. En contraste, un GIC de interés compuesto de cinco años como el discutido en la sección abridor recibe un depósito de intereses anualmente. Después de un año el principal aumenta de $15,000 a $15,892.50. Este principal superior en el segundo año explica por qué los intereses ganados en el segundo año también aumentan entonces.

Invierta $1,000 por 25 años tanto al 10% de interés simple como al 10% de interés compuesto anualmente. Como se demuestra en la figura y tabla a continuación, $1,000 invertidos al 10% anual de interés simple tiene un saldo de $3,500 después de 25 años. Esto consiste en el principal original de $1,000 más $2,500 en interés total ($100 por cada año que se invirtió el dinero). No obstante, $1,000 invertidos al 10% compuesto anualmente tiene un saldo de $10,834.71, ¡que es $7,334.71 más! Esta diferencia es el resultado de que los intereses se convierten en principal y por lo tanto ganan aún más interés para usted. Un examen minucioso de los dos primeros años revela lo siguiente:

En el primer año, ambas inversiones tienen un saldo de $1,100. Con intereses simples, los $100 de interés permanecen como intereses devengados y no se colocan en la cuenta mientras el principal se mantiene en $1,000. Con interés compuesto, los $100 de interés se convierten a principal, resultando en un principal de $1,100 para el segundo año.
En el segundo año, la cuenta de interés simple aún tiene un principal de $1,000, lo que gana otros $100 de interés ($1,000 × 10% = $100). La cuenta cuenta ahora tiene $1,000 de principal más $200 en intereses devengados. La cuenta de interés compuesto gana 10% sobre el nuevo principal de $1,100, o $110 de interés ($\$ 1,100 \times 10 \%=\$ 110$). Este interés se coloca en la cuenta al cierre del segundo año, haciendo el principal $1,210 para el tercer año.. y así sucesivamente.

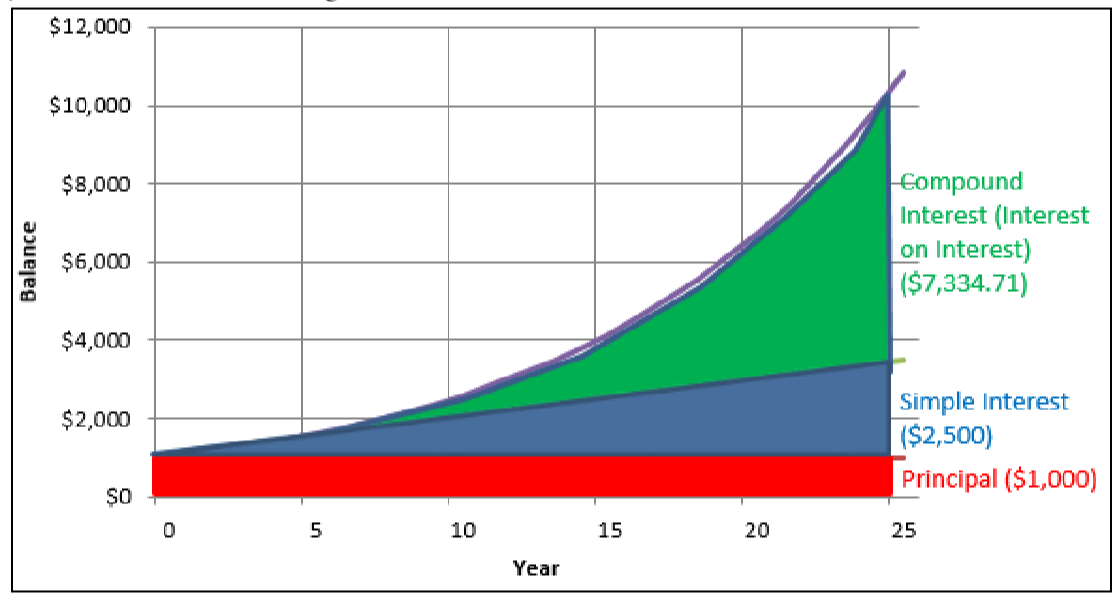
$clipboard_ea979fb9e1ec54ec38d3c444222ef8a15.png$

Figura$\PageIndex{1}$

	Al 10% de Interés Simple			Al 10% de Interés Compuesto
Fin de año	Principal	Intereses devengados	Saldo	Principal	Intereses devengados	Saldo
Inicio						$1,000.00
1	$1,000.00	$100.00	$1,100.00	$1,000.00	$100.00	$1,100.00
2	$1,000.00	$200.00	$1,200.00	$1,100.00	$110.00	$1,210.00
3	$1,000.00	$300.00	$1,300.00	$1,210.00	$121.00	1,331.00
4	$1,000.00	$400.00	$1,400.00	1,331.00	$133.10	1,464.10
5	$1,000.00	$500.00	$1,500.00	1,464.10	146.41	$1,610.51
	...	...	...	...	...	...
10	$1,000.00	$1,000.00	$2,000.00	2,357.95	235.79	2,593.74
	...	...	...	...	...	...
15	$1,000.00	$1500.00	$2,500.00	3,797.50	$379.75	$4,177.25
	...	...	...	...	...	...
20	$1,000.00	$2000.00	$3,000.00	$6,115.91	$611.59	$6,727.50
	...	...	...	...	...	...
25	$1,000.00	$2500.00	$3,500.00	$9.849.73	$984.98	10,834.71

En última instancia, a medida que aumenta el principal en la cuenta de intereses compuestos, también aumenta el monto de los intereses devengados. Observe que la diferencia en el equilibrio entre el interés simple y el interés compuesto en los primeros cinco años es leve, pero la brecha se amplía con el tiempo.

Tasas de interés compuestas

Si una cantidad igual de principal invertido durante 25 años gana una tasa de interés del 9% compuesto anual frente al 3% compuesto anualmente, ¿el interés acumulado por la inversión del 9% sería tres veces mayor?

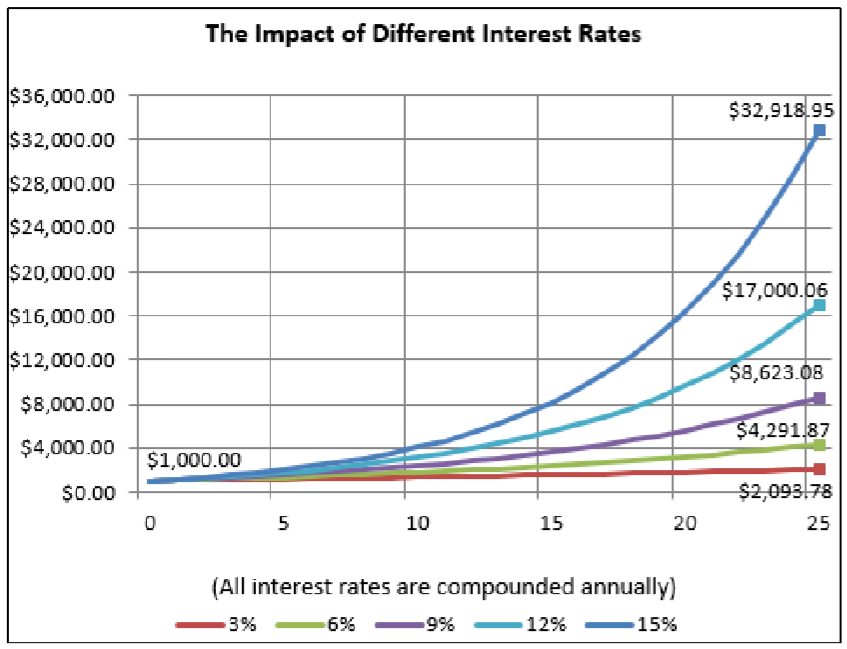
$clipboard_ea0163cbeda71ad09d20320fcfcc804b8.png$

Figura$\PageIndex{2}$

En un entorno de interés simple, esto sería cierto ya que el principal nunca cambia: en cada uno de los 25 años los montos de interés simple serían constantes, y el monto por la inversión del 9% sería tres veces mayor que para la inversión del 3%. Sin embargo, en interés compuesto, el interés de cada año subsiguiente se compone de un principal cada vez más grande. Este gráfico muestra $1,000 invertidos a cinco tasas compuestas anuales diferentes. Observar lo siguiente después de 25 años:

La inversión al 9% compuesta anualmente tiene un saldo de $8,623.08 en comparación con los $2,093.78 para el 3% compuesto anualmente. Por lo tanto, el interés devengado es de $7,623.08 frente a $1,093.78, reflejando una relación que se aproxima a 7:1.
Al comparar la tasa de interés del 15% frente a la tasa de interés del 6%, mucha gente imagina que los saldos finales estarían en la misma proporción que la relación de las tasas, 15%: 6%, lo que simplifica a 2½: 1. Sin embargo, en el gráfico, los saldos finales son $32.918.95 frente a $4,291.87, reflejando una relación que se aproxima a 7⅔: ¡1!

Estos ejemplos ilustran que en escenarios de interés compuesto, la relación de intereses devengados no es directamente proporcional a la relación numérica de las tasas de interés. Las tasas de interés más altas resultan en mayores cantidades de interés, por lo tanto, arrojan más capital sobre el que se devengan A lo largo de un largo periodo de tiempo, este crecimiento en la balanza es exponencial.

Con qué frecuencia los compuestos de interés

Los ejemplos hasta ahora han consistido en intereses compuestos que se han compuesto anualmente; los intereses devengados se están convirtiendo en principal al final de cada año. Pero esta no es la única opción. Los intereses se pueden convertir a principal con cualquier frecuencia, incluyendo diaria, semanal, mensual, trimestral (cada tres meses) o semestral (cada seis meses). Bajo cualquiera de estas opciones el principal aumenta con mayor frecuencia, lo que a su vez da como resultado que se ganen más intereses.

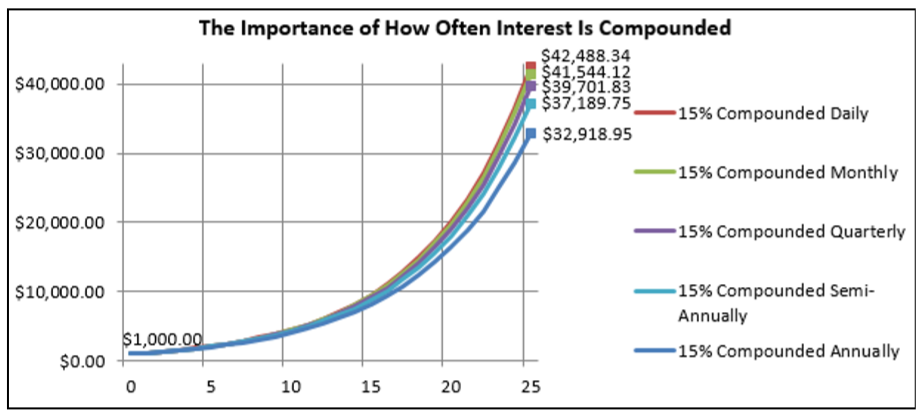
$clipboard_e7d316282c80bb1f2575e24c493a65679.png$

Figura e$\PageIndex{3}$

El gráfico de la figura anterior ilustra el impacto de diferentes frecuencias de composición. En el caso de la composición mensual versus anual, el compuesto mensual aumenta el saldo de la cuenta cada mes mientras que el compuesto anual aumenta el saldo una vez cada 12 meses. Para entender por qué el compuesto mensual gana más intereses, tenga en cuenta que después de cada mes el principal aumenta y por lo tanto gana más intereses. Cada uno de los 12 aumentos es pequeño por sí solo, pero el efecto acumulativo es grande: al tener los intereses depositados cada mes en lugar de cada año, en el transcurso de 25 años un adicional$\$ 41,544.12-\$ 32,918.95=\$ 8,625.17$ in interest is earned!

Caminos hacia el éxito

En la siguiente tabla se resumen las características deseables a la hora de invertir o pedir prestado.

Invertir	Característica	Préstamo
Compuesto	Tipo de Interés	Sencillo
Quieres que tus intereses te ganen más intereses.		No quieres que los intereses se conviertan en principal.
\[{\color {green} \Bigg \Uparrow} \nonumber \] Cuanto mayor sea la tasa, más ganarás.	Tasa de interés	\[{\color {red} \Bigg \Downarrow} \nonumber \] Cuanto menor sea la tasa, menos pagas.
\[{\color {green} \Bigg \Uparrow} \nonumber \] Cuanto más a menudo se agrava, más capital puede ganar intereses. ¡Un compuesto diario sería lo mejor!	Compounding	\[{\color {red} \Bigg \Downarrow} \nonumber \] Cuanto menos frecuentemente se agrava, menos capital puede ganar intereses. ¡Un compuesto anual sería lo mejor!
\[{\color {green} \Bigg \Uparrow} \nonumber \] A medida que el principal crece continuamente, ganas más intereses. Son deseables marcos de tiempo más largos.	Tiempo (o Término)	\[{\color {red} \Bigg \Downarrow} \nonumber \] No quieres que el director crezca y gane más intereses. Los plazos cortos son deseables.

Cálculo de la tasa de interés periódica

El primer paso para aprender sobre la inversión o el préstamo bajo interés compuesto es comprender la tasa de interés utilizada para convertir el interés en principal. Comúnmente necesita convertir la tasa de interés registrada para encontrar la tasa exacta de interés ganada o cobrada en un período de tiempo determinado.

La Fórmula

La Fórmula 9.1 involucra cuatro conceptos clave, los cuales se explican a continuación, que tienen que ver con la conversión de la tasa de interés.

$clipboard_e6b4e6fb412bf963e369fe1e2680c2fda.png$

Fórmula 9.1

Cómo funciona

Para resolver cualquier duda relacionada con la tasa de interés periódica, siga estos pasos:

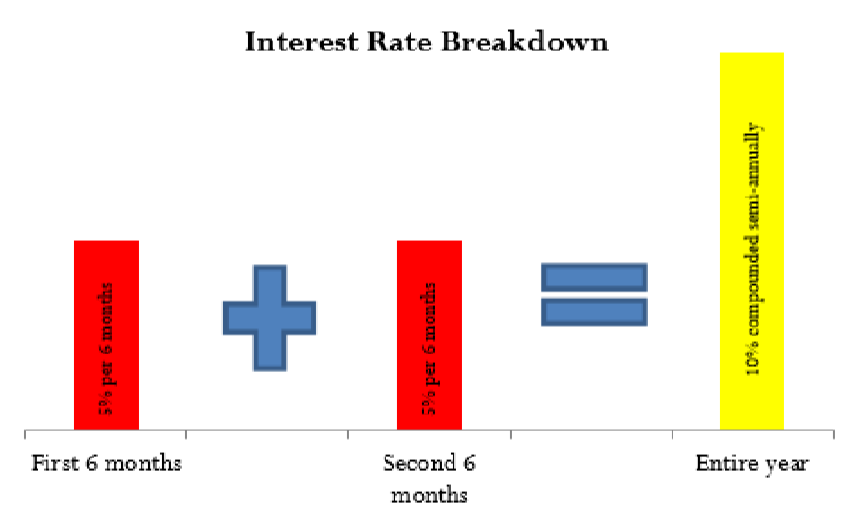
$clipboard_ecc60204a0ec83e900ae61e8a36bee40f.png$

Figura e$\PageIndex{4}$

Paso 1: Identificar dos de las tres variables clave: la tasa de interés nominal ($IY$), la frecuencia de capitalización ($CY$) o la tasa de interés periódica ($i$).

Paso 2: Sustituir a la Fórmula 9.1, reorganizar si es necesario, y resolver para la variable desconocida. Si calculas la frecuencia compuesta ($CY$), debes convertir el número de nuevo en las palabras compuestas asociadas a la frecuencia. Por ejemplo,$CY$ = 2 significa dos veces al año y se afirma como “semestral”.

Un ejemplo que implica el cálculo de la tasa de interés periódica para “10% compuesto semestral” ilustra estos pasos.

Paso 1: La redacción “semestral” significa que el periodo de composición es cada seis meses. Un año contiene dos de esos períodos compuestos, haciendo que la frecuencia de composición sea dos veces al año, o$CY$ = 2. La tasa de interés anual nominal es del 10%, o$IY$ = 10%.

Paso 2: Aplicando la Fórmula 9.1, calcule la tasa de interés periódica como$i=10 \% \div 2=5 \%$. La figura$\PageIndex{4}$ ilustra que cada seis meses el 5% de interés se convierte a principal. Se podría ver la tasa de interés nominal del año, 10%, como el total de las tasas de interés periódicas para cada uno de los dos periodos. Pero recuerde, a diferencia del simple interés, el monto real de interés aquí aumentará de un periodo a otro.

Notas Importantes

Cuando expresas una tasa de interés compuesta, siempre debes indicar las palabras para la frecuencia compuesta junto con el número nominal anual. Por ejemplo, hay que decir “10% compuesto semestralmente” y no sólo "10%”. En ausencia de una frecuencia de composición explícita, el número se interpreta por defecto en el sentido de “compuesto anualmente” excepto si un estándar de la industria dicta lo contrario. Por ejemplo, en el caso de las hipotecas en Canadá, el impago es la capitalización semestral, por lo que cuando escuche de una hipoteca del 10%, debe asumir que es un 10% compuesta semestral. Pero en la mayoría de las industrias “10%” sin palabras generalmente significa “10% compuesto anualmente”.

Cosas a tener en cuenta

Es común confundir el período de composición y la frecuencia de composición. La siguiente tabla muestra la relación entre periodos compuestos y frecuencias. Recuerda que para calcular la tasa de interés periódica necesitas la frecuencia de composición, no el periodo compuesto.

Compuestos Comunes	Periodo de composición	Frecuencia de composición ($CY$)
Anualmente	Todos los años	\ (CY\)) ">1
Semestral	Cada 6 meses	\ (CY\)) ">2
Trimestral	Cada 3 meses	\ (CY\)) ">4
Mensual	Cada 1 mes	\ (CY\)) ">12
Semanal	Cada 1 semana	\ (CY\)) ">52*
Diario	Todos los días	\ (CY\)) ">365*

*Tenga en cuenta que aunque no hay exactamente 52 semanas en un año y hay 366 días en un año bisiesto, es una práctica común utilizar estos valores para componer la frecuencia.

Caminos hacia el éxito

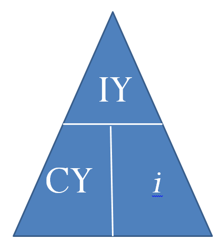
Para facilitar la manipulación, puedes recordar el reordenamiento de la Fórmula 9.1 usando una vez más la técnica tria ngle. Recuerda que mientras conozcas dos piezas cualesquiera del rompecabezas, podrás resolver para la tercera.

$clipboard_e111ef3c20ad04be7f6089ce506dacadd.png$

Ejercicio$\PageIndex{1}$: Give It Some Thought

Si estás invirtiendo dinero, ¿qué características de interés debes buscar?
Si estás pidiendo dinero prestado, ¿qué características de interés debes buscar?
De 10% compuesto semestral o 10% compuesto mensual, ¿cuál gana más intereses?
Si invirtió un principal a la misma tasa de interés compuesta durante 20 años, ¿el monto de los intereses ganados en los segundos 10 años sería menos del doble, exactamente el doble o más del doble del interés ganado durante los primeros 10 años?
John tiene una tasa de interés del 4% compuesta anualmente mientras que Dwayne está ganando 8% compuesto anualmente. Si ambas personas colocaran el mismo capital en sus inversiones durante 25 años, ¿Dwayne tendría el doble, menos del doble o más del doble de dinero que John?
De 10% interés simple o 10% interés compuesto anualmente, ¿cuál gana más interés con el tiempo?
De la tasa de interés periódica o la tasa de interés nominal, que siempre es al menos tan grande como la otra?

Responder

Alta tasa de interés, alta frecuencia de composición, marcos de tiempo largos, interés compuesto.
Baja tasa de interés, baja frecuencia de composición, plazos cortos, interés simple.
10% mensual, como se demuestra en la Figura$\PageIndex{3}$.
Más del doble, como se demuestra en la Figura$\PageIndex{2}$.
Más del doble, como se demuestra en la Figura$\PageIndex{2}$.
10% compuesto anualmente, como se demuestra en la Figura$\PageIndex{1}$.
La tasa de interés nominal.

Ejemplo$\PageIndex{1}$: The Periodic Interest Rate

Calcule la tasa de interés periódica para las siguientes tasas de interés nominales:

9% compuesto mensual
6% compuesto trimestral

Solución

Para cada pregunta, calcule la tasa de interés periódica ($i$).

Lo que ya sabes

Paso 1:

Para cada pregunta, utilice la siguiente tasa de interés nominal y frecuencia de composición:

$IY$= 9%;$CY$ = mensual = 12 veces al año
$IY$= 6%;$CY$ = trimestral = 4 veces al año

Cómo Llegarás

Paso 2:

Para cada pregunta aplica la Fórmula 9.1.

Realizar

$i=\dfrac{9 \%}{12}=0.75 \%$por mes
$i=\dfrac{6 \%}{4}=1.5 \%$por trimestre

Presente

El nueve por ciento compuesto mensual es igual a una tasa de interés periódica de 0.75% mensual. Esto significa que los intereses se convierten a principal 12 veces a lo largo del año a una tasa de 0.75% cada vez.
Seis por ciento compuesto trimestral es igual a una tasa de interés periódica de 1.5% por trimestre. Esto significa que los intereses se convierten a principal 4 veces (cada tres meses) a lo largo del año a una tasa de 1.5% cada vez.

Ejemplo$\PageIndex{2}$: The Nominal Interest Rate

Calcule la tasa de interés nominal para las siguientes tasas de interés periódicas:

$0.58 \overline{3} \%$por mes
$0.05 \%$por día

Solución

Para cada pregunta, calcule la tasa de interés nominal ($IY$).

Lo que ya sabes

Paso 1:

Para cada pregunta, utilice la siguiente tasa de interés periódica y frecuencia de composición:

$i=0.58 \overline{3} \%$;$CY$ = mensual = 12 veces al año
$i = 0.05 \% $;$CY$ = diario = 365 veces al año

Cómo Llegarás

Paso 2:

Para cada pregunta, aplique la Fórmula 9.1 y reorganice para$IY$.

Realizar

$0.58 \overline{3} \%=\dfrac{1 Y}{12}$;$IY=0.58 \overline{3} \% \times 12=7 \%$ compuesto mensual
$0.05 \%=\dfrac{I Y}{365}$;$IY = 0.05\% × 365 = 18.25\%$ compuesto diario

Presente

Una$0.58 \overline{3} \%$ tasa de interés periódica mensual es igual a una tasa de interés nominal de 7% compuesta mensual.
Una tasa de interés periódica de 0.05% por día es igual a una tasa de interés nominal de 18.25% compuesta diariamente.

Ejemplo$\PageIndex{3}$: Compounds per Year

Calcular la frecuencia de composición para las siguientes tasas de interés nominales y periódicas:

tasa de interés nominal = 6%, tasa de interés periódica = 3%
tasa de interés nominal = 9%, tasa de interés periódica = 2.25%

Solución

Para cada pregunta, calcule la frecuencia de composición ($CY$) y convierta el número calculado a palabras.

Lo que ya sabes

Paso 1:

Para cada pregunta, utilice las siguientes tasas de interés nominales y periódicas:

$IY$= 6%;$i$ = 3%
$IY$= 9%;$i$ = 2.25%

Cómo Llegarás

Paso 2:

Para cada pregunta, aplique la Fórmula 9.1 y reorganice para$CY$.

Realizar

$3 \%=\dfrac{6 \%}{CY}$;$CY=\dfrac{6 \%}{3 \%}=2$ compuestos por año = semestralmente
$2.25 \%=\dfrac{9 \%}{C Y}$;$CY=\dfrac{9 \%}{2.25 \%}=4$ compuestos por año = trimestralmente

Presente

Para que la tasa de interés nominal del 6% sea igual a una tasa de interés periódica del 3%, la frecuencia de capitalización debe ser dos veces al año, lo que significa un período compuesto de cada seis meses, o semestral.
Para que la tasa de interés nominal del 9% sea igual a una tasa de interés periódica de 2.25%, la frecuencia de capitalización debe ser cuatro veces al año, lo que significa un periodo compuesto de cada tres meses, o trimestral.

Colaboradores y Atribuciones

Template:ContribBusiMathOlivier

Search

Ejercicio\(\PageIndex{1}\): Give It Some Thought

Ejemplo\(\PageIndex{1}\): The Periodic Interest Rate

Ejemplo\(\PageIndex{2}\): The Nominal Interest Rate

Ejemplo\(\PageIndex{3}\): Compounds per Year