4.2: Maximización por el Método Simplex
- Page ID
- 113705
En esta sección, aprenderá a resolver problemas de maximización de programación lineal utilizando el Método Simplex:
- Identificar y configurar un programa lineal en forma de maximización estándar
- Convertir restricciones de desigualdad en ecuaciones usando variables de holgura
- Configurar el cuadro simplex inicial usando la función objetiva y ecuaciones de holgura
- Encuentre el cuadro simplex óptimo realizando operaciones de pivotamiento.
- Identificar la solución óptima a partir del cuadro simplex óptimo.
En el último capítulo, se utilizó el método geométrico para resolver problemas de programación lineal, pero el enfoque geométrico no funcionará para problemas que tengan más de dos variables. En situaciones de la vida real, los problemas de programación lineal consisten literalmente en miles de variables y son resueltos por computadoras. Podemos resolver estos problemas algebraicamente, pero eso no va a ser muy eficiente. Supongamos que nos dieron un problema con, digamos, 5 variables y 10 restricciones. Al elegir todas las combinaciones de cinco ecuaciones con cinco incógnitas, podríamos encontrar todos los puntos de esquina, probarlos para su viabilidad y llegar a la solución, si existe. Pero el problema es que incluso para un problema con tan pocas variables, obtendremos más de 250 puntos de esquina, y probar cada punto será muy tedioso. Entonces necesitamos un método que tenga un algoritmo sistemático y pueda programarse para una computadora. El método tiene que ser lo suficientemente eficiente para que no tengamos que evaluar la función objetiva en cada punto de esquina. Tenemos justamente tal método, y se llama el método simplex.
El método simplex fue desarrollado durante la Segunda Guerra Mundial por el Dr. George Dantzig. Sus modelos de programación lineal ayudaron a las fuerzas aliadas con problemas de transporte y programación. En 1979, un científico soviético llamado Leonid Khachian desarrolló un método llamado algoritmo elipsoide que se suponía que era revolucionario, pero resultó que no es mejor que el método simplex. En 1984, Narendra Karmarkar, un científico investigador de AT&T Bell Laboratories desarrolló el algoritmo de Karmarkar que ha demostrado ser cuatro veces más rápido que el método simplex para ciertos problemas. Pero el método simplex sigue funcionando mejor para la mayoría de los problemas.
El método simplex utiliza un enfoque que es muy eficiente. No calcula el valor de la función objetiva en cada punto; en cambio, comienza con un punto de esquina de la región de factibilidad donde todas las variables principales son cero y luego se mueve sistemáticamente de punto de esquina a punto de esquina, al tiempo que mejora el valor de la función objetivo en cada etapa. El proceso continúa hasta encontrar la solución óptima.
Para aprender el método simplex, intentamos un enfoque bastante poco convencional. Primero enumeramos el algoritmo, y luego trabajamos un problema. Justificamos el razonamiento detrás de cada paso durante el proceso. Una justificación minuciosa está más allá del alcance de este curso.
Comenzamos con un ejemplo que resolvimos en el último capítulo por el método gráfico. Esto nos proporcionará una idea del método simplex y al mismo tiempo nos dará la oportunidad de comparar algunas de las soluciones factibles que obtuvimos previamente por el método gráfico. Pero primero, enumeramos el algoritmo para el método simplex.
- Configura el problema. Es decir, escribir la función objetiva y las restricciones de desigualdad.
- Convertir las desigualdades en ecuaciones. Esto se hace agregando una variable de holgura por cada desigualdad.
- Construye el cuadro simplex inicial. Escribe la función objetivo como la fila inferior.
- La entrada más negativa en la fila inferior identifica la columna pivotante.
- Calcular los cocientes. El cociente más pequeño identifica una fila. El elemento en la intersección de la columna identificada en el paso 4 y la fila identificada en este paso se identifica como el elemento pivote. Los cocientes se calculan dividiendo la columna del extremo derecho por la columna identificada en el paso 4. Se ignora un cociente que sea un cero, o un número negativo, o que tenga un cero en el denominador.
- Realice el pivotamiento para que todas las demás entradas en esta columna sean cero. Esto se hace de la misma manera que lo hicimos con el método Gauss-Jordan.
- Cuando no hay más entradas negativas en la fila inferior, estamos terminados; de lo contrario, partimos de nuevo desde el paso 4.
- Lee tus respuestas. Obtener las variables usando las columnas con 1 y 0s. Todas las demás variables son cero. El valor máximo que buscas aparece en la esquina inferior derecha.
Ahora, utilizamos el método simplex para resolver el Ejemplo 3.1.1 resuelto geométricamente en la sección 3.1.
Niki tiene dos empleos de medio tiempo, Job I y Job II. Ella nunca quiere trabajar más de un total de 12 horas a la semana. Ella ha determinado que por cada hora que trabaja en el Trabajo I, necesita 2 horas de tiempo de preparación, y por cada hora que trabaja en el Job II, necesita una hora de tiempo de preparación, y no puede gastar más de 16 horas en preparación. Si gana $40 la hora en el Trabajo I, y $30 la hora en el Trabajo II, ¿cuántas horas debe trabajar a la semana en cada trabajo para maximizar sus ingresos?
Solución
Para resolver este problema, seguiremos el algoritmo enumerado anteriormente.
PASO 1. Configura el problema. Escribe la función objetiva y las restricciones.
Dado que el método simplex se utiliza para problemas que constan de muchas variables, no es práctico usar las variables\(x\)\(y\),\(z\) etc. usamos símbolos\(x_1\),\(x_2\),\(x_3\), y así sucesivamente.
Let
- \(x_1\)= El número de horas semanales Niki trabajará en el Job I y
- \(x_2\)= El número de horas semanales Niki trabajará en el Job II.
Se acostumbra elegir la variable que se va a maximizar como\(Z\).
El problema se formula de la misma manera que lo hicimos en el último capítulo.
\ [\ begin {array} {ll}
\ textbf {Maximizar} &\ mathrm {Z} =40\ mathrm {x} _ {1} +30\ mathrm {x} _ {2}\
\ textbf {Sujeto a:} &\ mathrm {x} _ {1} +\ mathrm {x} _ {2}\ leq 12\\
& 2\ mathrm {x} _ {1} +\ mathrm {x} _ {2}\ leq 16\\
&\ mathrm {x} _ {1}\ geq 0;\ mathrm {x} _ {2}\ geq 0
\ end {array}\ nonumber\]
PASO 2. Convertir las desigualdades en ecuaciones. Esto se hace agregando una variable de holgura por cada desigualdad.
Por ejemplo, para convertir la desigualdad\(x_1 + x_2 ≤ 12\) en una ecuación, agregamos una variable no negativa\(y_1\), y obtenemos
\[x_1 + x_2 + y_1 = 12 \nonumber \]
Aquí la variable\(y_1\) recoge la holgura, y representa la cantidad por la cual\(x_1 + x_2\) queda por debajo de 12. En este problema, si Niki trabaja menos de 12 horas, digamos 10, entonces\(y_1\) es 2. Posteriormente, cuando leemos la solución final de la tabla simplex, los valores de las variables de holgura identificarán las cantidades no utilizadas.
Reescribimos la función objetiva\(Z = 40x_1 + 30x_2\) como\(- 40x_1 - 30x_2 + Z = 0\).
Después de agregar las variables de holgura, nuestro problema dice
\ [\ begin {array} {ll}
\ text {Función objetiva} & - 40x_1 - 30x_2 + Z = 0\\
\ text {Sujeto a restricciones:} & x_1 + x_2 + y_1 = 12\\
& 2x_1 + x_2 + y_2 = 16\\
& x1 ≥ 0; x2 ≥ 0
\ end {array}\ nonumber\]
PASO 3. Construye el cuadro simplex inicial. Cada restricción de desigualdad aparece en su propia fila. (Las restricciones de no negatividad no aparecen como filas en el cuadro simplex). Escribe la función objetivo como la fila inferior.
Ahora que las desigualdades se convierten en ecuaciones, podemos representar el problema en una matriz aumentada llamada el cuadro simplex inicial de la siguiente manera.
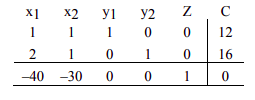
Aquí la línea vertical separa el lado izquierdo de las ecuaciones del lado derecho. La línea horizontal separa las restricciones de la función objetiva. El lado derecho de la ecuación está representado por la columna C.
El lector necesita observar que las últimas cuatro columnas de esta matriz parecen la matriz final para la solución de un sistema de ecuaciones. Si elegimos arbitrariamente\(x_1 = 0\) y\(x_2 = 0\), obtenemos
\ [\ left [\ begin {array} {ccccc}
y_ {1} & y_ {2} & Z & | & C\\
1 & 0 & 0 & | & 12\\
0 & 1 & 0 & | & 16\\ 0 &
0 & 0 & 0 & | & 0 & | & 0
\ end {array}\ derecha]\ nonumber\]
que dice
\[y_1 = 12 \quad y_2 = 16 \quad Z = 0 \nonumber \]
La solución obtenida asignando arbitrariamente valores a algunas variables y luego resolviendo para las variables restantes se llama la solución básica asociada al cuadro. Entonces, la solución anterior es la solución básica asociada con el cuadro simplex inicial. Podemos etiquetar la variable de solución básica a la derecha de la última columna como se muestra en la siguiente tabla.
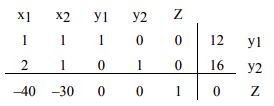
PASO 4. La entrada más negativa en la fila inferior identifica la columna pivotante.
La entrada más negativa en la fila inferior es -40; por lo tanto, se identifica la columna 1.
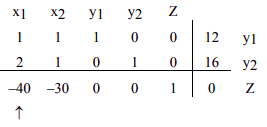
Pregunta ¿Por qué elegimos la entrada más negativa en la fila inferior?
Respuesta La entrada más negativa en la fila inferior representa el coeficiente más grande en la función objetiva - el coeficiente cuya entrada aumentará el valor de la función objetivo más rápido.
El método simplex comienza en un punto de esquina donde todas las variables principales, las variables que tienen símbolos como\(x_1\)\(x_2\),,\(x_3\) etc., son cero. Luego se mueve de un punto de esquina al punto de esquina adyacente aumentando siempre el valor de la función objetivo. En el caso de la función objetiva\(Z = 40x_1+ 30x_2\), tendrá más sentido aumentar el valor de\(x_1\) en lugar de\(x_2\). La variable\(x_1\) representa el número de horas semanales Niki trabaja en el Job I. Dado que el Trabajo I paga $40 por hora a diferencia de Job II que paga solo $30, la variable\(x_1\) incrementará la función objetiva en $40 por una unidad de incremento en la variable\(x_1\).
PASO 5. Calcular los cocientes. El cociente más pequeño identifica una fila. El elemento en la intersección de la columna identificada en el paso 4 y la fila identificada en este paso se identifica como el elemento pivote.
Siguiendo el algoritmo, para calcular el cociente, dividimos las entradas en la columna del extremo derecho por las entradas de la columna 1, excluyendo la entrada en la fila inferior.
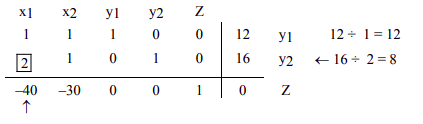
El menor de los dos cocientes, 12 y 8, es 8. Por lo tanto, se identifica la fila 2. La intersección de la columna 1 y la fila 2 es la entrada 2, la cual ha sido resaltada. Este es nuestro elemento pivote.
Pregunta ¿Por qué encontramos cocientes y por qué el cociente más pequeño identifica una fila?
Respuesta Cuando elegimos la entrada más negativa en la fila inferior, estamos tratando de aumentar el valor de la función objetiva incorporando la variable\(x_1\). Pero no podemos elegir ningún valor para\(x_1\). ¿Podemos dejar\(x_1 = 100\)? ¡Definitivamente no! Eso es porque Niki nunca quiere trabajar más de 12 horas en ambos trabajos combinados:\(x_1 + x_2 ≤ 12\). ¿Podemos dejar\(x_1 = 12\)? Nuevamente, la respuesta es no porque el tiempo de preparación para Job I es el doble del tiempo dedicado al trabajo. Como Niki nunca quiere dedicar más de 16 horas a la preparación, el tiempo máximo que puede trabajar es de 16 ÷ 2 = 8.
Ahora ve el propósito de computar los cocientes; usar los cocientes para identificar el elemento pivote garantiza que no violamos las restricciones.
Pregunta ¿Por qué identificamos el elemento pivote?
Respuesta Como hemos mencionado anteriormente, el método simplex comienza con un punto de esquina y luego se mueve al siguiente punto de esquina mejorando siempre el valor de la función objetiva. El valor de la función objetiva se mejora cambiando el número de unidades de las variables. Podemos sumar el número de unidades de una variable, mientras tiramos a la basura las unidades de otra. El pivotar nos permite hacer precisamente eso.
La variable cuyas unidades se están agregando se llama la variable de entrada, y la variable cuyas unidades se están reemplazando se llama la variable de salida. La variable de ingreso en la tabla anterior es\(x_1\), y fue identificada por la entrada más negativa en la fila inferior. La variable de salida\(y_2\) se identificó por el menor de todos los cocientes.
PASO 6. Realice el pivotamiento para que todas las demás entradas en esta columna sean cero.
En el capítulo 2, se utilizó el pivotamiento para obtener la forma de escalón de fila de una matriz aumentada. Pivotar es un proceso de obtener un 1 en la ubicación del elemento pivote, y luego hacer todas las demás entradas ceros en esa columna. Entonces ahora nuestro trabajo es hacer de nuestro elemento pivote un 1 dividiendo toda la segunda fila por 2. El resultado sigue.
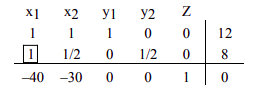
Para obtener un cero en la entrada primero por encima del elemento pivote, multiplicamos la segunda fila por -1 y la agregamos a la fila 1. Obtenemos

Para obtener un cero en el elemento debajo del pivote, multiplicamos la segunda fila por 40 y la agregamos a la última fila.
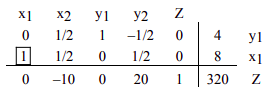
Ahora determinamos la solución básica asociada a este cuadro. Al elegir arbitrariamente\(x_2 = 0\) y\(y_2 = 0\), obtenemos\(x_1 = 8\),\(y_1 = 4\), y\(z = 320\). Si escribimos la matriz aumentada, cuyo lado izquierdo es una matriz con columnas que tienen uno 1 y todas las demás entradas ceros, obtenemos la siguiente matriz que indica lo mismo.
\ [\ left [\ begin {array} {ccccc}
\ mathrm {x} _ {1} &\ mathrm {y} _1 &\ mathrm {Z} & | &\ mathrm {C}\\ 0 &\
0 & 1 & 0 & | & 4\\
1 & 0 & 0 & 0 & | & 8\ 0 &
0 & 0 & 0 & 0 & 0 & | & 320
\ end {array}\ derecha]\ nonumber\]
Podemos reafirmar la solución asociada a esta matriz como\(x_1 = 8\),\(x_2 = 0\),\(y_1 = 4\),\(y_2 = 0\) y\(z = 320\). En esta etapa del juego, se lee que si Niki trabaja 8 horas en el Job I, y ninguna hora en el Job II, su ganancia Z será de 320 dólares. Recordemos del Ejemplo 3.1.1 en la sección 3.1 que (8, 0) fue uno de nuestros puntos de esquina. Aquí\(y_1 = 4\) y\(y_2 = 0\) significa que se quedará con 4 horas de tiempo de trabajo y sin tiempo de preparación.
PASO 7. Cuando no hay más entradas negativas en la fila inferior, estamos terminados; de lo contrario, partimos de nuevo desde el paso 4.
Dado que todavía hay una entrada negativa, -10, en la fila inferior, necesitamos comenzar, nuevamente, desde el paso 4. Esta vez no vamos a repetir los detalles de cada paso, en cambio, identificaremos la columna y fila que nos dan el elemento pivote, y resaltaremos el elemento pivote. El resultado es el siguiente.
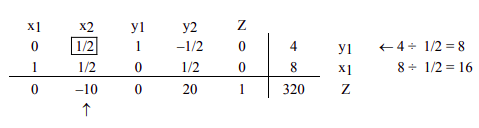
Hacemos el elemento pivote 1 multiplicando la fila 1 por 2, y obtenemos
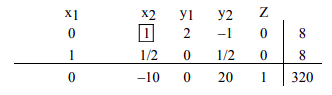
Ahora para hacer todas las demás entradas como ceros en esta columna, primero multiplicamos la fila 1 por -1/2 y la agregamos a la fila 2, y luego multiplicamos la fila 1 por 10 y la agregamos a la fila inferior.
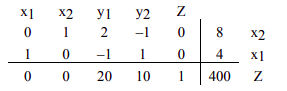
Ya no tenemos entradas negativas en la fila inferior, por lo tanto estamos terminados.
Pregunta ¿Por qué terminamos cuando no hay entradas negativas en la fila inferior?
Respuesta La respuesta se encuentra en la fila inferior. La fila inferior corresponde a la ecuación:
\ [\ begin {array} {l}
0 x_ {1} +0 x_ {2} +20 y_ {1} +10 y_ {2} +Z=400\ quad\ text {o}\\
z=400-20 y 1-10 y 2
\ end {array}\ nonumber\]
Dado que todas las variables son no negativas, el valor más alto que jamás se\(Z\) puede lograr es 400, y eso ocurrirá sólo cuando\(y_1\) y\(y_2\) sean cero.
PASO 8. Lee tus respuestas.
Ahora leemos nuestras respuestas, es decir, determinamos la solución básica asociada al cuadro simplex final. Nuevamente, miramos las columnas que tienen un 1 y todas las demás entradas ceros. Como las columnas etiquetadas\(y_1\) y no\(y_2\) son tales columnas, elegimos arbitrariamente\(y_1 = 0\), y\(y_2 = 0\), y obtenemos
\ [\ left [\ begin {array} {ccccc}
\ mathrm {x} _ {1} &\ mathrm {x} _ {2} &\ mathrm {Z} & | &\ mathrm {C}\\ 0 &\ 0 & 1 & 0 & | & 8\\ 1 &
0 & 0 & | & 4\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 &
0 & 0 & 0 & 0 & 0 & 1 & | & 400
\ end {array}\ derecha] \ nonumber\]
La matriz lee\(x_1 = 4\),\(x_2= 8\) y\(z = 400\).
La solución final dice que si Niki trabaja 4 horas en el Job I y 8 horas en el Job II, maximizará sus ingresos a $400. Dado que ambas variables de holgura son cero, significa que ella habría gastado todo el tiempo de trabajo, así como el tiempo de preparación, y no quedará ninguna.


