8.2: Sucesos mutuamente excluyentes y la regla de adición

Última actualización
Guardar como PDF

Page ID: 113747

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

En esta sección, aprenderás a:

Defina eventos compuestos usando unión, intersección y complemento.
Identificar eventos mutuamente excluyentes
Utilice la Regla de Adición para calcular la probabilidad de uniones de eventos.

En el último capítulo aprendimos a encontrar la unión, intersección y complemento de un conjunto. Ahora usaremos estas operaciones de conjunto para describir eventos.

La unión de dos eventos E y F, E$\cup$ F, es el conjunto de resultados que están en E o en F o en ambos.
La intersección de dos eventos E y F, E$\cap$ F, es el conjunto de resultados que se encuentran tanto en E como en F.
El complemento de un evento E, denotado por E ^c, es el conjunto de resultados en el espacio muestral S que no están en E.

Es de destacar que P (E ^c) = 1 - P (E). Esto se deduce del hecho de que si el espacio muestral tiene$n$ elementos y E tiene$k$ elementos, entonces E ^c tiene$n - k$ elementos. Por lo tanto,

\[P\left(E^{c}\right)=\frac{n-k}{n}=1-\frac{k}{n}=1-P(E) \nonumber \]

De particular interés para nosotros son los eventos cuyos resultados no se superponen. A estos eventos los llamamos mutuamente excluyentes.

Se dice que dos eventos E y F son mutuamente excluyentes si no se cruzan: E$\cap$ F =$\varnothing$.

A continuación determinaremos si un par determinado de eventos son mutuamente excluyentes.

Ejemplo$\PageIndex{1}$

Una carta es extraída de una baraja estándar. Determinar si el par de eventos que se indican a continuación es mutuamente excluyente.

E = {La carta extraída es un As}

F = {La carta extraída es un corazón}

Solución

Claramente el as de corazones pertenece a ambos conjuntos. Eso es

\[\mathrm{E} \cap \mathrm{F}=\{\text { Ace of hearts }\} \neq \varnothing \nonumber \]

Por lo tanto, los eventos E y F no son mutuamente excluyentes.

Ejemplo$\PageIndex{2}$

Se rotan dos dados. Determinar si el par de eventos que se indican a continuación es mutuamente excluyente.

G = {La suma de las caras es seis}

H = {Un dado muestra un cuatro}

Solución

Para mayor claridad, enumeramos los elementos de ambos conjuntos.

G = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)} y H = {(2, 4), (4, 2)}

Claramente, G$\cap$ H = {(2, 4), (4, 2)}$\neq \varnothing$.

Por lo tanto, los dos conjuntos no son mutuamente excluyentes.

Ejemplo$\PageIndex{3}$

Una familia tiene tres hijos. Determinar si el siguiente par de eventos son mutuamente excluyentes.

M = {La familia tiene al menos un niño}

N = {La familia tiene todas las niñas}

Solución

Aunque la respuesta puede ser clara, enumeramos ambos conjuntos.

M = {BBB, BBG, BGB, BGG, GBB, GBG, GGB} y N = {GGG}

Claramente, M$\cap$ N =$\varnothing$

Por lo tanto, los eventos M y N son mutuamente excluyentes.

Ahora vamos a considerar problemas que involucran la unión de dos hechos.

Dados dos eventos, E, F, entonces encontrar la probabilidad de E$\cup$ F, es lo mismo que encontrar la probabilidad de que E suceda, o F sucederá, o ambos sucederán.

Ejemplo$\PageIndex{4}$

Si se enrolla un dado, ¿cuál es la probabilidad de obtener un número par o un número mayor a cuatro?

Solución

Sea E el evento de que el número mostrado en el dado sea un número par, y que F sea el evento de que el número mostrado sea mayor que cuatro.

El espacio muestral S = {1, 2, 3, 4, 5, 6}. El evento E = {2, 4, 6} y el evento F = {5, 6}

Tenemos que encontrar P (E$\cup$ F).

Dado que P (E) = 3/6, y P (F) = 2/6, un estudiante puede decir P (E$\cup$ F) = 3/6 + 2/6. Esto será incorrecto porque el elemento 6, que está tanto en E como en F se ha contado dos veces, una como elemento de E y una vez como elemento de F. En otras palabras, el conjunto E$\cup$ F tiene sólo cuatro elementos y no cinco: conjunto E$\cup$ F = {2,4,5,6}

Por lo tanto, P (E$\cup$ F) = 4/6 y no 5/6.

Esto se puede ilustrar mediante un diagrama de Venn. Usaremos el Diagrama de Venn para reexaminar Ejemplo$\PageIndex{4}$ y derivar una regla de probabilidad que podemos usar para calcular probabilidades para uniones de eventos.

A continuación se enumeran el espacio muestral S, los eventos E y$\cap$ F y E F.

\[\mathrm{S}=\{1,2,3,4,5,6\}, \mathrm{E}=\{2,4,6\}, \mathrm{F}=\{5,6\}, \text { and } \mathrm{E} \cap \mathrm{F}=\{6\} \nonumber. \nonumber \]

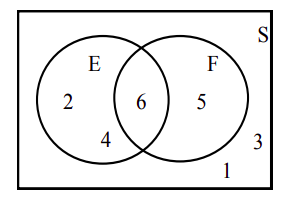
$Sección8.2.png$

La figura anterior muestra S, E, F y E$\cap$ F.

Encontrar la probabilidad de E$\cup$ F, es lo mismo que encontrar la probabilidad de que E suceda, o F sucederá, o ambas sucederán.

Si contamos el número de elementos n (E) en E, y le sumamos el número de elementos n (F) en F, los puntos tanto en E como en F se cuentan dos veces, una vez como elementos de E y una vez como elementos de F. Ahora si restamos de la suma, n (E) + n (F), el número n (E$\cap$ F), eliminamos la duplicidad y obtenemos la correcta respuesta. Entonces, por regla general,

\[\mathrm{n}(\mathrm{E} \cup \mathrm{F})=\mathrm{n}(\mathrm{E})+\mathrm{n}(\mathrm{F})-\mathrm{n}(\mathrm{E} \cap \mathrm{F}) \nonumber \]

Al dividir toda la ecuación por n (S), obtenemos

\[\frac{\mathrm{n}(\mathrm{E} \cup \mathrm{F})}{\mathrm{n}(\mathrm{S})}=\frac{\mathrm{n}(\mathrm{E})}{\mathrm{n}(\mathrm{S})}+\frac{\mathrm{n}(\mathrm{F})}{\mathrm{n}(\mathrm{S})}-\frac{\mathrm{n}(\mathrm{E} \cap \mathrm{F})}{\mathrm{n}(\mathrm{S})} \nonumber \]

Dado que la probabilidad de un evento es el número de elementos en ese evento dividido por el número de todos los resultados posibles, tenemos

\[\mathrm{P}(\mathrm{E} \cup \mathrm{F})=\mathrm{P}(\mathrm{E})+\mathrm{P}(\mathrm{F})-\mathrm{P}(\mathrm{E} \cap \mathrm{F}) \nonumber \]

Aplicando lo anterior por Ejemplo$\PageIndex{4}$, obtenemos

\[\mathrm{P}(\mathrm{E} \cup \mathrm{F})=3 / 6+2 / 6-1 / 6=4 / 6 \nonumber \]

Esto se debe a que, cuando sumamos P (E) y P (F), hemos agregado P (E$\cap$ F) dos veces. Por lo tanto, debemos restar P (E$\cap$ F), una vez.

Esto nos da la fórmula general, llamada Regla de Adición, para encontrar la probabilidad de la unión de dos eventos. Debido a que el evento E$\cup$ F es el evento que E va a suceder, O F sucederá, O ambos sucederán, a veces llamamos a esto la Regla de Adición para Eventos OR. Afirma

Regla de Adición

\[\mathbf{P}(\mathbf{E} \cup \mathbf{F})=\mathbf{P}(\mathbf{E})+\mathbf{P}(\mathbf{F})-\mathbf{P}(\mathbf{E} \cap \mathbf{F}) \nonumber \]

Si, y solo si, dos eventos$\mathrm{E}$ y$\mathrm{F}$ son mutuamente excluyentes, entonces$\mathrm{E} \cap \mathrm{F}=\varnothing$ y$\mathrm{P}(\mathrm{E} \cap \mathrm{F})=0$, y obtenemos$\mathrm{P}(\mathrm{E} \cup \mathrm{F})=\mathrm{P}(\mathrm{E})+\mathrm{P}(\mathrm{F})$

Ejemplo$\PageIndex{5}$

Si se saca una carta de un mazo, usa la regla de adición para encontrar la probabilidad de obtener un as o un corazón.

Solución

Que A sea el evento de que la carta sea un as, y H el evento de que sea un corazón.

Como hay cuatro ases, y trece corazones en la baraja,

P (A) = 4/52 y P (H) = 13/52.

Además, dado que la intersección de dos eventos consiste en una sola carta, el as de corazones, ahora tenemos:

P (A$\cap$ H) = 1/52

Necesitamos encontrar P (A$\cup$ H):

\ begin {alineado}
\ mathrm {P} (\ mathrm {A}\ copa\ mathrm {H}) &=\ mathrm {P} (\ mathrm {A}) +\ mathrm {P} (\ mathrm {H}) -\ mathrm {P} (\ mathrm {A}\ cap\ mathrm {H})\\
&=4/52+13/52-1/52=16/52
\ final {alineado}

Ejemplo$\PageIndex{6}$

Se tiran dos dados, y los eventos F y T son los siguientes:

F = {La suma de los dados es cuatro} y T = {Al menos un dado muestra un tres}

Encuentra P (F$\cup$ T).

Solución

Enumeramos F y T, y F$\cap$ T de la siguiente manera:

F = {(1, 3), (2, 2), (3, 1)}

T = {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (1, 3), (2, 3), (4, 3), (5, 3), (6, 3)}

F$\cap$ T = {(1, 3), (3, 1)}

Puesto que P (F$\cup$ T) = P (F) + P (T) - P (F$\cap$ T)

Tenemos P (F$\cup$ T) = 3/36 + 11/36 - 2/36 = 12/36.

Ejemplo$\PageIndex{7}$

El señor Washington está buscando un puesto de instructor de matemáticas en su colegio comunitario favorito en Cupertino. Su empleo depende de dos condiciones: si la junta aprueba el puesto, y si el comité de contratación lo selecciona. Hay un 80% de posibilidades de que la junta apruebe el puesto, y hay un 70% de posibilidades de que el comité de contratación lo seleccione. Si hay un 90% de posibilidades de que se cumpla al menos una de las dos condiciones, la aprobación de la junta directiva o su selección, ¿cuál es la probabilidad de que se contrate al señor Washington?

Solución

Que A sea el evento en el que la junta apruebe la posición, y S sea el evento que el señor Washington sea seleccionado. Tenemos,

P (A) = .80, P (S) = .70 y P (A$\cup$ S) = .90.

Tenemos que encontrar, P (A$\cap$ S).

La fórmula de adición establece que,

\[P(A \cup S)=P(A)+P(S)-P(A \cap S) \nonumber \]

Sustituyendo los valores conocidos, obtenemos

\[.90=.80+.70-P(\mathrm{A} \cap \mathrm{S}) \nonumber \]

Por lo tanto, P (A$\cap$ S) = .60.

Ejemplo$\PageIndex{8}$

La probabilidad de que este fin de semana sea frío es de .6, la probabilidad de que sea lluvioso es de .7, y la probabilidad de que sea tanto frío como lluvioso es de .5. ¿Cuál es la probabilidad de que no sea ni frío ni lluvioso?

Solución

Que C sea el evento de que el fin de semana sea frío, y R sea evento que va a ser lluvioso. Se nos da que

\[\mathrm{P}(\mathrm{C})=.6, \quad \mathrm{P}(\mathrm{R})=.7, \quad \mathrm{P}(\mathrm{C} \cap \mathrm{R})=.5 \nonumber \]

Primero encontramos P (C$\cup$ R) usando la Regla de Adición.

\[P(C \cup R) = P(C) + P(R) - P(C \cap R) = .6 + .7 - .5 = .8 \nonumber \]

Entonces encontramos P ((C$\cup$ R) ^c) usando la Regla Complemento.

\[P\left((C \cup R)^{c}\right)=1-P(C \cup R)=1-.8=.2 \nonumber \]

Resumimos esta sección enumerando las reglas importantes.

Resumen

La regla de adición

Para Dos Eventos$\mathrm{E}$ y$\mathrm{F}$,$\mathrm{P}(\mathrm{E} \cup \mathrm{F})=\mathrm{P}(\mathrm{E})+\mathrm{P}(\mathrm{F})-\mathrm{P}(\mathrm{E} \cap \mathrm{F})$

La regla de adición para eventos mutuamente excluyentes

Si Dos Eventos$\mathrm{E}$ y$\mathrm{F}$ son Mutuamente Exclusivos, entonces$\mathrm{P}(\mathrm{E} \cup \mathrm{F})=\mathrm{P}(\mathrm{E})+\mathrm{P}(\mathrm{F})$

La regla del complemento

Si$\mathrm{E}^c$ es el Complemento del Evento$\mathrm{E}$, entonces$\mathrm{P}(\mathrm{E}^c) = 1 - \mathrm{P}(\mathrm{E})$

Objetivos de aprendizaje

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Ejemplo\(\PageIndex{3}\)

Ejemplo\(\PageIndex{4}\)

Regla de Adición

Ejemplo\(\PageIndex{5}\)

Ejemplo\(\PageIndex{6}\)

Ejemplo\(\PageIndex{7}\)

Ejemplo\(\PageIndex{8}\)

Resumen