10.5: REVISIÓN DEL CAP

Última actualización
Guardar como PDF

Page ID: 113829

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

SECCIÓN 10.5 CONJUNTO DE PROBLEMAS: REVISIÓN DEL CAPÍTULO

¿La matriz que se da a continuación es una matriz de transición para una cadena de Markov? Explique.
1. \ (\ left [\ begin {array} {ccc}
  .1 & .4 & .5\\
  .5 & -.3 & .8\\
  .3 & .4 & .3
  \ end {array}\ right]\)
2. \ (\ left [\ begin {array} {ccc}
  .2 & .6 & .2\\
  0 & 0 & 0\\
  .3 & .4 & .5
  \ end {array}\ right]\)
Una encuesta a compradores de computadoras indica que si una persona compra una computadora Apple, hay un 80% de posibilidades de que su próxima compra sea una Apple, mientras que los propietarios de una computadora con Windows volverán a comprar una computadora con Windows con una probabilidad de .70. Los hábitos de compra de estos consumidores están representados en la matriz de transición a continuación.

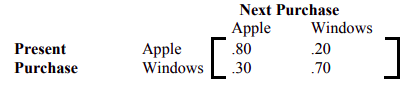
$Sección10.5.5-2.png$

Encuentra la probabilidad de que un actual propietario de una computadora Apple compre una computadora con Windows como su siguiente computadora.
Encuentra la probabilidad de que un actual propietario de una computadora Apple compre una computadora con Windows como su tercera computadora.
Encuentra la probabilidad de que un propietario actual de una computadora con Windows compre una computadora con Windows como su cuarta computadora.

El profesor Trayer enseña Matemáticas Finitas o Estadística cada trimestre. Nunca enseña Matemáticas Finitas dos trimestres consecutivos, pero si enseña Estadística un cuarto, entonces el siguiente trimestre enseñará Estadística con una probabilidad de 1/3.
1. Escribir una matriz de transición para este problema.
2. Si la profesora Trayer enseña Matemáticas Finitas en el trimestre de Otoño, cuál es la probabilidad de que enseñe Estadística en el trimestre de Invierno.
3. Si la profesora Trayer enseña Matemáticas Finitas en el trimestre de Otoño, cuál es la probabilidad de que enseñe Estadística en el trimestre de Primavera.
Determinar si las siguientes matrices son cadenas regulares de Markov.
1. \ (\ left [\ begin {array} {ll}
  1 & 0\\
  .3 & .7
  \ end {array}\ right]\)
2. \ (\ left [\ begin {array} {lll}
  .2 & .4 & .4\\
  .6 & .4 & 0\\
  .3 & .2 & .5
  \ end {array}\ right]\)
La matriz de transición para cambiar las carreras académicas cada trimestre por parte de los estudiantes de una universidad se da a continuación, donde las carreras de Ciencias, Negocios y Artes Liberales se denotan con S, B y A, respectivamente.

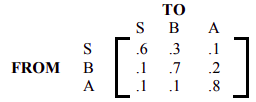
$Sección10.5.5-5.png$

Encuentre la probabilidad de que un estudiante de ciencias pase a una especialización en negocios durante su primer trimestre.
Encuentra la probabilidad de que un estudiante de negocios pase a un Artes Liberales durante su segundo trimestre.
Encuentra la probabilidad de que un estudiante de ciencias pase a Liberal Artsr durante su tercer trimestre.

John Elway, el mariscal de campo de fútbol de los Broncos de Denver, calificó sus propias jugadas. En cada jugada tenía que decidir ya sea pasar la pelota o entregarla. La matriz de transición para sus jugadas se da en la siguiente tabla, donde P representa un pase y H un traspaso.

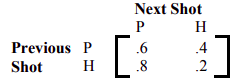
$Sección10.5.5-6.png$

Si John Elway lanzó un pase en la jugada inicial, ¿cuál es la probabilidad de que entregara traspaso en las dos jugadas después?
Determinar la distribución del juego a largo plazo.

La Compañía I, la Compañía II y la Compañía III compiten entre sí, y la matriz de transición para las personas que pasan de empresa a empresa cada año se da a continuación.

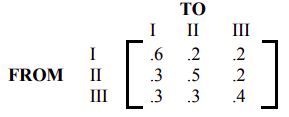
$Sección10.5.5-7.png$

Si la cuota de mercado inicial es de 20% para la Compañía I, 30% para la Compañía II y 50% para la Compañía III, ¿cuál será la participación de mercado después del próximo año?
Si esta tendencia continúa, ¿cuál es la expectativa de largo alcance para el mercado?

Dada la siguiente cadena absorbente de Markov.

$Sección10.5.5-8.png$

Identificar los estados absorbentes.
Escriba la matriz de soluciones.
Partiendo del estado 4, ¿cuál es la probabilidad de absorción eventual en el estado 1?
Partiendo del estado 3, ¿cuál es la probabilidad de absorción eventual en el estado 2?

Un ratón colocado en el laberinto se mueve de una habitación a otra al azar. De cualquier habitación, el ratón elegirá una puerta a la habitación contigua con iguales probabilidades. Una vez que llega a la habitación 1, encuentra comida y nunca sale de esa habitación. Y cuando llega a la habitación 6, queda atrapada y no puede salir de esa habitación. ¿Cuál es la probabilidad de que el ratón termine en la habitación 1 si inicialmente se colocó en la habitación 3?

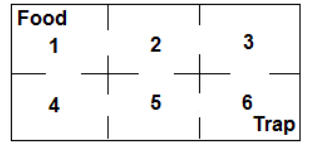
$Sección10.5.5-9.png$

¿Cuál es la probabilidad de que el ratón termine en la habitación 6 si inicialmente estaba en la habitación 2?