11.2: Juegos No Estrictamente Determinados
- Page ID
- 113779
En esta sección, estudiamos juegos que no tienen puntos de silla de montar. Esto quiere decir que estos juegos no poseen una estrategia pura. A estos juegos los llamamos juegos no estrictamente determinados. Si el juego se juega solo una vez, no hará ninguna diferencia qué movimiento se haga. Sin embargo, si el juego se juega repetidamente, se puede elaborar una estrategia mixta que consiste en alternar movimientos aleatorios.
Consideramos el siguiente ejemplo.
Supongamos que Robert y Carol deciden jugar un juego usando un centavo y un cuarto. A una señal dada, muestran simultáneamente una de las dos monedas. Si las monedas coinciden, Robert obtiene ambas monedas, pero si no coinciden, Carol obtiene ambas monedas. Determinar si el juego está estrictamente determinado.
Solución
Escribimos la matriz de pago para Robert de la siguiente manera:
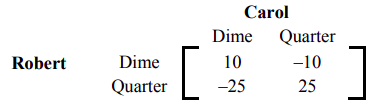
Para determinar si el juego está estrictamente determinado, buscamos un punto de silla de montar. Nuevamente, colocamos un asterisco junto al valor mínimo en cada fila, y una caja alrededor del valor máximo en cada columna. Obtenemos
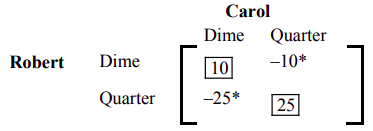
Dado que no hay entrada que tenga tanto un asterisco como una caja, el juego no tiene un punto de silla de montar, y por lo tanto no está estrictamente determinado.
Deseamos idear una estrategia para Robert. Si Robert muestra consistentemente un centavo, por ejemplo, Carol verá el patrón y comenzará a mostrar un cuarto, y Robert perderá. Por el contrario, si Carol muestra repetidamente un cuarto, Robert comenzará a mostrar un cuarto, resultando así en la pérdida de Carol. Entonces una buena estrategia es echar a tu oponente mostrando un centavo algunas de las veces y mostrando un cuarto otras veces. Antes de desarrollar una estrategia óptima para cada jugador, consideraremos una estrategia arbitraria para cada uno y determinaremos los beneficios correspondientes.
Supongamos en Ejemplo\(\PageIndex{1}\), Robert decide mostrar una moneda de diez centavos con .20 de probabilidad y un cuarto con .80 de probabilidad, y Carol decide mostrar una moneda de diez centavos con una probabilidad de.70 y un cuarto con una probabilidad de.30. ¿Cuál es el pago esperado para Robert?
Solución
Que R denote la estrategia de Robert y C denote la estrategia de Carol.
Como Robert es jugador de fila y Carol es jugador de columna, sus estrategias están escritas de la siguiente manera:
\ [\ mathrm {R} =\ left [\ begin {array} {ll}
.20 & .80
\ end {array}\ right]\ text {y} C=\ left [\ begin {array} {l}
.70\\
.30
\ end {array}\ right]\ nonumber. \ nonumber\]
Para encontrar el beneficio esperado, utilizamos el siguiente razonamiento.
Ya que Robert elige jugar la fila 1 con probabilidad de.20 y Carol elige jugar la columna 1 con una probabilidad de.70, el movimiento fila 1, columna 1 se elegirá con (.20) (.70) = .14 probabilidad. El hecho de que esta jugada tenga un pago de 10 centavos para Robert, la ganancia esperada de Robert para esta jugada es de (.14) (.10) = .014 centavos. De igual manera, calculamos los beneficios esperados de Robert para los otros casos. La siguiente tabla enumera los resultados esperados para los cuatro casos.
| Mover | Probabilidad | Reembolso | Reembolso esperado |
|---|---|---|---|
| Fila 1, Columna 1 | (.20) (.70) = .14 | 10 centavos | 1.4 centavos |
| Fila 1, Columna 2 | (.20) (.30) = .06 | -10 centavos | -.6 centavos |
| Fila 2, Columna 1 | (.80) (.70) = .56 | -25 centavos | -14 centavos |
| Fila 2, Columna 2 | (.80) (.30) = .24 | 25 centavos | 6.0 centavos |
| Totales | 1 | -7.2 centavos |
La tabla anterior muestra que si Robert juega el juego con la estrategia\ (\ mathrm {R} =\ left [\ begin {array} {ll}
.20 & .80
\ end {array}\ right]\) y Carol juega con la estrategia\ (\ mathrm {C} =\ left [\ begin {array} {l}
.70\\
.30
\ end {array}\ derecha]\), Robert puede esperar perder 7.2 centavos por cada partido.
Alternativamente, si llamamos a la matriz de juego G, entonces el beneficio esperado para el jugador de fila se puede determinar multiplicando las matrices R, G y C. Así, el pago esperado P para Robert es el siguiente:
\ [\ begin {array} {l}
\ mathrm {P} =\ mathrm {RGC}\
\ mathrm {P} =\ left [\ begin {array} {cc}
.20 & .80
\ end {array}\ derecha]\ left [\ begin {array} {cc}
10 & -10\\
-25 & 25
\ end {array}\ derecha]\ izquierda [\ begin {array} {c}
.70\\
.30
\ end {array}\ derecho]\\
\ mathrm {P} =-7.2\:\ mathrm {centavos}
\ end {array}\ nonumber\]
que es el mismo que el obtenido de la tabla.
Para la siguiente matriz de juego G, determine la estrategia óptima tanto para el jugador de fila como para el jugador de columna, y encuentre el valor del juego.
\ [G=\ left [\ begin {array} {cc}
1 & -2\\
-3 & 4
\ end {array}\ right]\ nonumber\]
Solución
Supongamos que el jugador de fila usa la estrategia\ (\ mathrm {R} =\ left [\ begin {array} {ll}
\ mathrm {r} & 1-\ mathrm {r}
\ end {array}\ right]\). Ahora bien, si el jugador de la columna juega la columna 1, el pago esperado P para el jugador de fila es
\[\mathrm{P}(r) = 1(r) + (-3)(1 - r) = 4r - 3. \nonumber \]
Esto también se puede calcular de la siguiente manera:
\ [\ mathrm {P} (r) =\ left [\ begin {array} {ll}
r & 1-r
\ end {array}\ right]\ left [\ begin {array} {c}
1\\
-3
\ end {array}\ right]\ text {o} 4 r-3\ nonumber\]
Si el jugador de fila juega la estrategia\ (\ left [\ begin {array} {ll}
\ mathrm {r} & 1-\ mathrm {r}
\ end {array}\ right]\) y el jugador de columna juega la columna 2, la ganancia esperada P para el jugador de fila es
\ [P (r) =\ left [\ begin {array} {ll}
r & 1-r
\ end {array}\ right]\ left [\ begin {array} {c}
-2\\
4
\ end {array}\ right] =-6 r+4\ nonumber\]
Tenemos dos ecuaciones:\(\mathrm{P}(r) = 4r - 3\) y\(\mathrm{P}(r) = -6r + 4\)
El jugador de fila está tratando de mejorar su peor escenario, y eso sólo sucede cuando las dos líneas se cruzan. Cualquier punto que no sea el punto de intersección no resultará en una estrategia óptima ya que una de las expectativas se quedará corta.
Resolviendo para\(r\) algebraicamente, obtenemos
\ [\ begin {array} {c}
4 r-3=-6 r+4\\
r=7/10
\ end {array}\ nonumber\]
Por lo tanto, la estrategia óptima para el jugador de fila es\ (\ left [\ begin {array} {ll}
.7 & .3
\ end {array}\ right]\).
Alternativamente, podemos encontrar la estrategia óptima para el jugador de fila, primero, multiplicando la matriz de filas con la matriz de juego como se muestra a continuación.
\ [\ left [\ begin {array} {ccc}
r & 1-r
\ end {array}\ right]\ left [\ begin {array} {cc}
1 & -2\\
-3 & 4
\ end {array}\ right] =\ left [\ begin {array} {cc}
4 r-3 & -6 r+4
\ end {array}\ right]\ nonumber\]
Y luego igualando las dos entradas en la matriz del producto. Nuevamente, obtenemos\(r = .7\), lo que nos da la estrategia óptima\ (\ left [\ begin {array} {ll}
.7 & .3
\ end {array}\ right]\).
Utilizamos la misma técnica para encontrar la estrategia óptima para el jugador de columna. Supongamos que la estrategia óptima del jugador de columnas está representada por\ (\ left [\ begin {array} {
c} c\\
1-c
\ end {array}\ right]\). Nosotros, primero, multiplicamos la matriz de juego por la matriz de columnas como se muestra a continuación.
\ [\ left [\ begin {array} {cc}
1 & -2\\
-3 & 4
\ end {array}\ right]\ left [\ begin {array} {c}
c\\
1-c
\ end {array}\ right] =\ left [\ begin {array} {c}
3 c-2\
-7 c+4
\ end {array}\ right]\ nonumber\]
Y luego equiparar las entradas en la matriz del producto. Obtenemos
\ [\ begin {array} {l}
3 c-2=-7 c+4\\
c=.6
\ end {array}\ nonumber\]
Por lo tanto, la estrategia óptima del jugador de columnas es\ (\ left [\ begin {array} {l}
.6\\
.4
\ end {array}\ right]\).
Para encontrar el valor esperado, V, del juego, encontramos el producto de las matrices R, G y C.
\ [\ begin {array} {l}
\ mathrm {V} =\ left [\ begin {array} {ll}
.7 & .3
\ end {array}\ right]\ left [\ begin {array} {cc}
1 & -2\\
-3 & 4
\ end {array}\ right]\ left [\ begin {array} {l}
.6\\
.4
\ end {array}\ derecha]\\
\ mathrm {V} =-.2
\ end {array}\ nonumber\]
Es decir, si ambos jugadores juegan sus estrategias óptimas, el jugador de fila puede esperar perder .2 unidades por cada juego.
Para el juego en Ejemplo\(\PageIndex{1}\), determina la estrategia óptima tanto para Robert como para Carol, y encuentra el valor del juego.
Solución
Como ya hemos determinado que el juego no está estrictamente determinado, se procede a determinar la estrategia óptima para el juego. Reescribimos la matriz del juego.
\ [G=\ left [\ begin {array} {cc}
10 & -10\\
-25 & 25
\ end {array}\ derecha]\ nonumber\]
Que\ (\ mathrm {R} =\ left [\ begin {array} {ll}
\ mathrm {r} & 1-\ mathrm {r}
\ end {array}\ right]\) sea la estrategia de Robert, y\ (C=\ left [\ begin {array} {c}
c\\
1-c
\ end {array}\ right]\) sea la estrategia de Carol.
Para encontrar la estrategia óptima para Robert, nosotros, primero, encontramos el producto RG de la siguiente manera.
\ [\ left [\ begin {array} {ccc}
\ mathrm {r} & 1-\ mathrm {r}
\ end {array}\ right]\ left [\ begin {array} {cc}
10 & -10\\
-25 & 25
\ end {array}\ right] =\ left [\ begin {array} {cc}
35\ mathrm {r} -25 & -35\ mathrm {r} +25
\ end {array}\ derecha]\ nonumber\]
Al establecer las entradas iguales, obtenemos
\[35r - 25 = -35r + 25 \nonumber \]
o\[ r = 5/7. \nonumber \]
Por lo tanto, la estrategia óptima para Robert es\ [\ left [\ begin {array} {ll}
5/7 & 2/7
\ end {array}\ right]. \ nonumber\]
Para encontrar la estrategia óptima para Carol, primero, encontramos el siguiente producto.
\ [\ left [\ begin {array} {cc}
10 & -10\\
-25 & 25
\ end {array}\ right]\ left [\ begin {array} {c}
c\\
1-c
\ end {array}\ right] =\ left [\ begin {array} {c}
20 c-10\\
-50 c+25
\ end {array}\ derecha]\ nonumber\]
Ahora establecemos las entradas iguales entre sí, y obtenemos,
\[20c - 10 = -50c + 25 \nonumber \]
o\[c = 1/2 \nonumber \]
Por lo tanto, la estrategia óptima para Carol es\ [\ left [\ begin {array} {l}
1/2\\
1/2
\ end {array}\ right]\ nonumber\].
Para encontrar el valor esperado, V, del juego, encontramos el producto RGC.
\ [\ begin {aligned}
\ mathrm {V} &=\ left [\ begin {array} {cc}
5/7 & 2/7
\ end {array}\ right]\ left [\ begin {array} {cc}
10 & -10\\
-25 & 25
\ end {array}\ right]\ left [\ begin {array} {c}
1/2\\
1/2
\ end {array}\ right]\\
&=\ left [\ begin {array} {c}
0
\ end {array}\ right]
\ end {aligned}\ nonumber\]
Si ambos jugadores juegan su estrategia óptima, el valor del juego es cero. En tal caso, el juego se llama justo.


