2.4: Mecánica de fluidos- Arrastre
- Page ID
- 112482
Los ejemplos anteriores mostraron que los casos fáciles pueden verificar y construir fórmulas, pero los ejemplos se pueden hacer sin casos fáciles (por ejemplo, con cálculo). Para las siguientes ecuaciones, a partir de la mecánica de fluidos, no se conocen soluciones exactas en general, por lo que los casos fáciles y otras herramientas de lucha en la calle son casi la única forma de avanzar.
Aquí están las ecuaciones Navier—Stokes de la mecánica de fluidos:
\[\frac{\partial \mathbf{v}}{\partial t}+(\mathbf{v} \cdot \boldsymbol{\nabla}) \mathbf{v}=-\frac{1}{\rho} \boldsymbol{\nabla} p+v \boldsymbol{\nabla}^{2} \mathbf{v}\label{2.13} \]
donde v es la velocidad del fluido (en función de la posición y el tiempo),\(ρ\) es su densidad,\(p\) es la presión, y\(ν\) es la viscosidad cinemática. Estas ecuaciones describen una increíble variedad de fenómenos que incluyen vuelo, tornados y rápidos fluviales.
Nuestro ejemplo es el siguiente experimento casero sobre drag. Fotocopia esta página mientras la magnifica por un factor de 2; luego corta las siguientes dos plantillas:
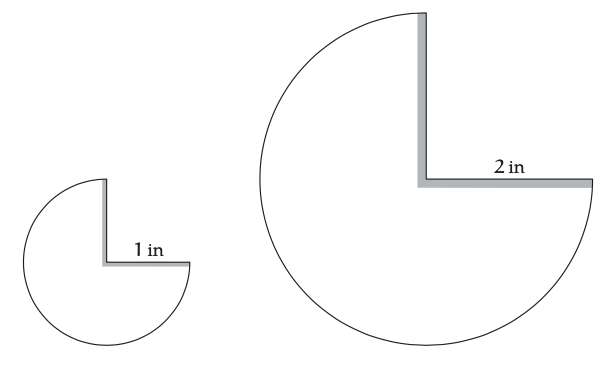
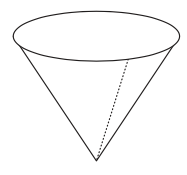
Con cada plantilla, pegue las áreas sombreadas para hacer un cono. Los dos conos resultantes tienen la misma forma, pero el cono grande tiene el doble de altura y ancho del cono pequeño.
Cuando los conos se dejan caer apuntan hacia abajo, ¿cuál es la relación aproximada de sus velocidades terminales (las velocidades a las que el arrastre equilibra el peso)?
Las ecuaciones Navier-Stokes contienen la respuesta a esta pregunta. Encontrar la velocidad del terminal implica cuatro pasos.
Paso 1. Imponer condiciones de contorno. Las condiciones incluyen el movimiento del cono y el requisito de que no ingrese fluido al papel.
Paso 2. Resolver las ecuaciones, junto con la ecuación de continuidad\(∇·v = 0\), para encontrar la presión y velocidad en la superficie del cono.
Paso 3. Use la presión y la velocidad para encontrar el gradiente de presión y velocidad en la superficie del cono; luego integre las fuerzas resultantes para encontrar la fuerza neta y el par en el cono.
Paso 4. Utilice la fuerza neta y el par para encontrar el movimiento del cono. Este paso es difícil porque el movimiento resultante debe ser consistente con el movimiento asumido en el paso 1. Si no es consistente, volver al paso 1, asumir una moción diferente, y esperar mejor suerte al llegar a este paso.
Desafortunadamente, las ecuaciones Navier-Stokes son ecuaciones acopladas y no lineales parcial-diferenciales. Sus soluciones se conocen sólo en casos muy simples: por ejemplo, una esfera que se mueve muy lentamente en un fluido viscoso, o una esfera que se mueve a cualquier velocidad en un fluido de viscosidad cero. Hay pocas esperanzas de resolver el complicado flujo alrededor de una forma irregular y temible como un cono de papel flexible.
Problema 2.12 Comprobación de dimensiones en las ecuaciones Navier—Stokes
Verifique que los tres primeros términos de las ecuaciones Navier-Stokes tengan dimensiones idénticas.
Problema 2.13 Dimensiones de la viscosidad cinemática
De las ecuaciones Navier-Stokes, encuentre las dimensiones de la viscosidad cinemática\(ν\).
Uso de cotas
Debido a que una solución directa de las ecuaciones Navier-Stokes está fuera de discusión, usemos los métodos de análisis dimensional y casos fáciles. Un enfoque directo es utilizarlos para deducir la propia velocidad terminal. Un enfoque indirecto es deducir la fuerza de arrastre en función de la velocidad de caída y luego encontrar la velocidad a la que el arrastre equilibra el peso de los conos. Este enfoque de dos pasos simplifica el problema. Introduce solo una nueva cantidad (la fuerza de arrastre) pero elimina dos cantidades: la aceleración gravitacional y la masa del cono.
¿Por qué la fuerza de arrastre es independiente de la aceleración gravitacional\(g\) y de la masa del cono\(m\) (pero la fuerza depende de la forma y tamaño del cono)?
El principio de dimensiones es que todos los términos en una ecuación válida tienen dimensiones idénticas.
Aplicada a la fuerza de arrastre\(F\), significa que en la ecuación\(F = f\) (cantidades que afectan a F) ambos lados tienen dimensiones de fuerza. Por lo tanto, la estrategia es encontrar las cantidades que afectan\(F\), encontrar sus dimensiones, y luego combinar las cantidades en una cantidad con dimensiones de fuerza.
¿De qué cantidades depende el arrastre y cuáles son sus dimensiones?
La fuerza de arrastre depende de cuatro cantidades: dos parámetros del cono y dos parámetros del fluido (aire). (Para las dimensiones de ν, ver Problema 2.13.)
| V | velocidad del cono | LT\(^{-1}\) |
| r | tamaño del cono | L |
| p | densidad del aire | ML\(^{-3}\) |
| v | viscosidad del aire | L\(^{2}\) T\(^{-1}\) |
¿Alguna combinación de los cuatro parámetros\(v\)\(r\),\(ρ\), y\(ν\) tiene dimensiones de fuerza?
El siguiente paso es combinar\(v\),,\(r\)\(ρ\), y\(ν\) en una cantidad con dimensiones de fuerza. Desafortunadamente, las posibilidades son numerosas, por ejemplo,
\[F_{1} = ρv^{2}r^{2}, F_{2} = ρνvr, \label{2.14} \]
o las combinaciones de productos\(\sqrt{F_{1}F_{2}} \text{ and } F_{1}^{2}/F_{2}\). Cualquier suma de estos\(1 \sqrt{2}\) productos feos también es una fuerza, por lo que la fuerza de arrastre\(F\) podría ser\(\sqrt{F1F2}\) +\(F_{1}^{2}/F_{2}\), 3\(\sqrt{F1F2} − 2F_{1}^{2}/F_{2}\), o mucho peor.
Reducir las posibilidades requiere un método más sofisticado que simplemente adivinar combinaciones con dimensiones correctas. Para desarrollar el enfoque sofisticado, regrese al primer principio de dimensiones: Todos los términos en una ecuación tienen dimensiones idénticas. Este principio se aplica a cualquier declaración sobre arrastre como
\[A + B = C \label{2.15} \]
donde las blobs\(A, B, \text{ and } C\) son funciones de\(F, v, r, ρ, \text{ and } ν\). Aunque las manchas pueden ser funciones absurdamente complejas, tienen dimensiones idénticas. Por lo tanto, dividiendo cada término por\(A\), lo que produce la ecuación
\[\frac{A}{A} + \frac{B}{A} = \frac{C}{A}, \label{2.16} \]
hace que cada término sea adimensional. El mismo método convierte cualquier ecuación válida en una ecuación adimensional. Así, cualquier ecuación (verdadera) que describa el mundo puede escribirse en una forma adimensional.
Cualquier forma adimensional se puede construir a partir de grupos adimensionales: a partir de productos adimensionales de las variables. Debido a que cualquier ecuación que describa el mundo se puede escribir en una forma adimensional, y cualquier forma adimensional se puede escribir usando grupos adimensionales, cualquier ecuación que describa el mundo se puede escribir usando grupos adimensionales.
¿El ejemplo de caída libre (Sección 1.2) es consistente con este principio?
Antes de aplicar este principio al complicado problema del arrastre, pruébelo en el sencillo ejemplo de caída libre (Sección 1.2). La velocidad exacta de impacto de un objeto caído desde una altura h es\(v = \sqrt{2gh}\), donde g es la aceleración gravitacional. De hecho, este resultado puede escribirse en la forma adimensional\(v/\sqrt{gh}\) =\(\sqrt{2}\), que a su vez usa solo el grupo adimensional\(v/\sqrt{gh}\). El nuevo principio pasa su primera prueba.
Este análisis de fórmulas adimensionales, cuando se invierte, se convierte en un método de síntesis. Vamos a calentar sintetizando la velocidad de impacto v. Primero, enumere las cantidades en el problema; aquí, son v, g y h. Segundo, combine estas cantidades en grupos adimensionales. Aquí, todos los grupos adimensionales se pueden construir solo a partir de un grupo. Para ese grupo, vamos a elegir\(v^{2}/gh\) (la elección particular no afecta la conclusión). Entonces la única declaración adimensional posible es
\[\frac{v^{2}}{gh} = \text{ dimensionless constant }\label{2.17} \]
(El lado derecho es una constante adimensional porque no hay un segundo grupo disponible para usar allí). En otras palabras,\(v^{2}/gh ∼ 1\) o\(v ∼ \sqrt{gh}\).
Este resultado reproduce el resultado del análisis dimensional menos sofisticado en la Sección 1.2. En efecto, con un solo grupo adimensional, cualquiera de los análisis lleva a la misma conclusión. Sin embargo, en problemas difíciles por ejemplo, encontrar la fuerza de arrastre el método menos sofisticado no proporciona su restricción en una forma útil; entonces el método de grupos adimensionales es esencial.
Problema 2.15 Tiempo de caída
Sintetizar una fórmula aproximada para el tiempo de caída libre\(t \text{ from } g \text{ and } h\).
Problema 2.16 Tercera ley de Kepler
Sintetizar la tercera ley de Kepler que conecta el período orbital de un planeta con su radio orbital. (Ver también Problema 1.15.)
¿Qué grupos adimensionales se pueden construir para el problema de arrastre?
Un grupo adimensional podría ser\(F/ρv^{2}r^{2}\); un segundo grupo podría ser rv/ν. Cualquier otro grupo puede ser construido a partir de estos grupos (Problema 2.17), por lo que el problema es descrito por dos grupos adimensionales independientes. La declaración adimensional más general es entonces
\[\text{ one group = f(second group) }, \label{2.18} \]
donde\(f\) es una función aún desconocida (pero adimensional).
¿Qué grupo adimensional pertenece en el lado izquierdo?
El objetivo es sintetizar una fórmula para\(F, \text{ and } F\) aparece sólo en el primer grupo\(F/ρv^{2}r^{2}\). Con esa restricción en mente, coloque el primer grupo en el lado izquierdo en lugar de envolverlo en la aún misteriosa función\(f\). Con esta elección, la afirmación más general sobre la fuerza de arrastre es
\[\frac{F}{pv^{2}r^{2}} = f\frac{rv}{v}. \label{2.19} \]
La física de la fuerza de arrastre (en estado estacionario) sobre el cono está contenida en la función adimensional\(f\).
Problema 2.17 Solo dos grupos
Mostrar que\(F, v, r, ρ, \text{ and } ν\) producen sólo dos grupos adimensionales independientes.
Problema 2.18 ¿Cuántos grupos en general?
¿Existe un método general para predecir el número de grupos adimensionales independientes? (La respuesta fue dada en 1914 por Buckingham [9].)
El procedimiento puede parecer inútil, habiendo producido una fuerza de arrastre que depende de la función desconocida f. Pero ha mejorado enormemente nuestras posibilidades de encontrar\(f\). La formulación original del problema requirió adivinar la función de cuatro variables h in\(F = h(v, r, ρ, ν)\), mientras que el análisis dimensional redujo el problema a adivinar una función de una sola variable (la relación\(vr/ν\)). El valor de esta simplificación fue elocuentemente descrito por el estadístico y físico Harold Jeffreys (citado en [34, p. 82]):
Una buena tabla de funciones de una variable puede requerir una página; la de una función de dos variables un volumen; la de una función de tres variables una librería; y la de una función de cuatro variables una biblioteca.
La pirámide truncada de la Sección 2.3 tiene volumen
\[V = \frac{1}{3}h (a^{2} + ab + b^{2}). \label{2.20} \]
Haga grupos adimensionales a partir de\(V, h, a, \text{ and } b\), y reescriba el volumen usando estos grupos. (Hay muchas maneras de hacerlo).
Uso de estuches fáciles
Aunque mejoradas, nuestras posibilidades no parecen altas: Incluso el problema de arrastre de una variable no tiene una solución exacta. Pero podría tener soluciones exactas en sus casos fáciles. Debido a que los casos más fáciles suelen ser casos extremos, mira primero los casos extremos.
¿Casos extremos de qué?
La función desconocida\(f\) depende únicamente de\(rv/ν\),
\[\frac{F}{pv^{2}r^{2}} = f \frac{rv}{v}, \label{2.21} \]
así que prueba extremos de\(rv/ν\). Sin embargo, para evitar caer en el empuje de símbolos sin sentido, primero determinar el significado de\(rv/ν\). Esta combinación\(rv/ν\), a menudo denotada Re, es el famoso número de Reynolds. (Su interpretación física requiere la técnica de agrupamiento y se explica en la Sección 3.4.3.) El número de Reynolds afecta la fuerza de arrastre a través de la función desconocida\(f\):
\[\frac{F}{pv^{2}r^{2}} = f(Re). \label{2.22} \]
Con suerte, se\(f\) puede deducir en extremos del número de Reynolds; con más suerte, los conos que caen son ejemplo de un extremo.
¿Los conos que caen son un extremo del número de Reynolds?
El número de Reynolds depende de\(r, v, \text{ and } ν\). Para la velocidad v, la experiencia cotidiana sugiere que los conos caen aproximadamente a 1 m\(s^{-1}\) (dentro de, digamos, un factor de 2). El tamaño\(r\) es aproximadamente 0.1 m (nuevamente dentro de un factor de 2). Y la viscosidad cinemática del aire es\(ν ∼ 10^{-5}m^{2}s^{-1}\). El número de Reynolds es
\[\frac{\overbrace{0.1 \mathrm{~m}}^{\mathrm{r}} \times \overbrace{1 \mathrm{~m} \mathrm{~s}^{-1}}^{v}}{\underbrace{10^{-5} \mathrm{~m}^{2} \mathrm{~s}^{-1}}_{\mathrm{v}}} \sim 10^{4}\label{2.23} \]
Es significativamente mayor que 1, por lo que los conos que caen son un caso extremo de alto número de Reynolds. (Para un número bajo de Reynolds, intente Problema 2.27 y vea [38].)
Estimación Re para un submarino que navega bajo el agua, un grano de polen que cae, una gota de lluvia que cae y un 747 que cruza el Atlántico.
El límite de número de Reynolds-alto se puede alcanzar de muchas maneras. Una forma es reducir la viscosidad\(ν \text{ to } 0\), porque ν vive en el denominador del número de Reynolds. Por lo tanto, en el límite de alto número de Reynolds, la viscosidad desaparece del problema y la fuerza de arrastre no debe depender de la viscosidad. Este razonamiento contiene varias falsedades sutiles, sin embargo su conclusión es mayormente correcta. (Aclarar las sutilezas requirió dos siglos de progreso en matemáticas, culminando en perturbaciones singulares y la teoría de las capas límite [12, 46].)
La viscosidad afecta la fuerza de arrastre solo a través del número de Reynolds:
\[\frac{F}{pv^{2}r^{2}} = f(\frac{rv}{v}). \label{2.34} \]
Para hacer\(F\) independiente de la viscosidad,\(F\) debe ser independiente del número de Reynolds! El problema entonces contiene solo un grupo adimensional independiente\(F/ρv^{2}r^{2}\), por lo que la declaración más general sobre el arrastre es
\[\frac{F}{pv^{2}r^{2}} = \text{ dimensional constant } \label{2.25} \]
La fuerza de arrastre en sí es entonces\(F ∼ ρv^{2}r^{2}\). Debido a que r es proporcional al área de la sección transversal del cono\(A\), la fuerza de arrastre se escribe comúnmente
\[F ∼ ρv^{2}A. \label{2.26} \]
Si bien la derivación fue para conos que caen, el resultado se aplica a cualquier objeto siempre y cuando el número de Reynolds sea alto. La forma afecta solo a la constante adimensional faltante. Para una esfera, es aproximadamente 1/4; para un cilindro largo que se mueve perpendicular a su eje, es aproximadamente 1/2; y para una placa plana que se mueve perpendicular a su cara, es aproximadamente
Velocidades terminales
El resultado\(F ∼ ρv^{2}A\) es suficiente para predecir las velocidades terminales de los conos. Velocidad terminal significa aceleración cero, por lo que la fuerza de arrastre debe equilibrar el peso. El peso es\(W = σ_{paper}A_{\text{paper}}g\), donde\(σ_{\text{paper}}\) está la densidad de área del papel (masa por área) y\(A_{\text{paper}}\) es el área de la plantilla después de cortar el cuarto de sección. Debido a que\(A_{\text{paper}}\) es comparable al área de la sección transversal\(A\), el peso se da aproximadamente por
\[W ∼ σ_{\text{paper}}Ag. \label{2.27} \]
Por lo tanto,
\[\underbrace{ρv^{2}A} \underbrace{∼ σ_{paper}Ag}.\label{2.28} \]
El área se divide y la velocidad terminal se convierte en
\[v \sim \sqrt{\frac{g \sigma_{\text {paper }}}{\rho}} \label{2.29} \]
¡Todos los conos construidos a partir del mismo papel y que tienen la misma forma, cualquiera que sea su tamaño, caen a la misma velocidad!
Para probar esta predicción, construí los conos pequeños y grandes descritos en la página 21, sostuve uno en cada mano sobre mi cabeza y los dejé caer. Su caída de 2m duró aproximadamente 2s, y aterrizaron dentro de 0.1s el uno del otro. ¡Experimento barato y teoría barata de acuerdo!
Problema 2.21 Experimento casero de un cono pequeño versus un cono grande
Prueba el experimento de cono casero tú mismo (página 21).
Problema 2.22 Experimento casero de cuatro conos apilados versus un cono
Predecir la relación
\[\frac{\text{ terminal velocity of four small cones stacked inside each other } }{ \text{ terminal velocity of one small cone }}. \label{2.30} \]
Pon a prueba tu predicción. ¿Puede encontrar un método que no requiera equipo de cronometraje?
Problema 2.23 Estimando la velocidad del terminal
Estimar o buscar la densidad de área del papel; predecir la velocidad terminal de los conos; y luego comparar esa predicción con el resultado del experimento doméstico.


