3.3: Estimación de Derivados
- Page ID
- 112614
En los ejemplos anteriores, la aglutinación ayudó a estimar integrales. Debido a que la integración y diferenciación están estrechamente relacionadas, la formación de grumos también proporciona un método para estimar derivados. El método comienza con una observación dimensional sobre derivados. Un derivado es una relación de diferenciales; por ejemplo,\(df/dx\) es la relación de\(df\) a\(dx\). Debido a que\(d\) es adimensional (Sección 1.3.2), las dimensiones de\(df/dx\) son las dimensiones de\(f/x\).
Esta conclusión útil y sorprendente vale la pena probar con un ejemplo familiar: Diferenciar la altura\(y\) con respecto al tiempo\(t\) produce velocidad\(dy/dt\), cuyas dimensiones de\(LT^{−1}\) son efectivamente las dimensiones de\(y/t\).
¿Cuáles son las dimensiones de\(d^{2}f/dx^{2}\)?
Aproximación Secante
Como\(df/dx\) y\(f/x\) tienen dimensiones idénticas, quizás sus magnitudes son similares:
\[\frac{df}{dx} ∼ \frac{f}{x}. \label{3.13} \]
Geométricamente, la derivada\(df/dx\) es la pendiente de la línea tangente, mientras que la aproximación\(f/x\) es la pendiente de la línea secante. Al reemplazar la curva por la línea secante, hacemos una aproximación de agrupamiento.
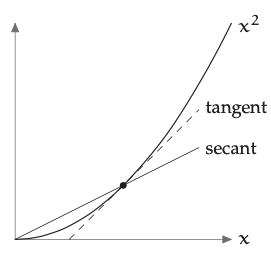
Probemos la aproximación en una función fácil como\(f(x) = x\). Buenas noticias las pendientes secante y tangente difieren solo por un factor de 2:
\[\frac{df}{dx} = 2x \text{ and } \frac{f(x)}{x} = x \label{3.14} \]
Investigar la aproximación secante para\(f(x) = x^{n}\).
Utilice la aproximación secante para estimar\(d^{2}f/dx^{2}\) con\(f(x) = x^{2}\). ¿Cómo se compara la aproximación con la segunda derivada exacta?
¿Qué tan precisa es la aproximación secante\(f(x) = x^{2} + 100\)?
La aproximación secante es rápida y útil pero puede cometer grandes errores. Cuando\(f(x) = x^{2} + 100\), por ejemplo, la secante y la tangente en\(x = 1\) tienen pendientes dramáticamente diferentes. La pendiente tangente df/dx es 2, mientras que la pendiente secante f (1) /1 es 101. La relación de estas dos pendientes, aunque adimensional, es angustiosamente grande.
Con\(f(x) = x^{2} + 100\), bosquejar la relación
\[\frac{ \text{ secant slope }}{\text{ tangent slope } } \label{3.15} \]
en función de\(x\). ¡La relación no es constante! ¿Por qué el factor adimensional no es constante? (Esa pregunta es complicada.)
La gran discrepancia en la sustitución del derivado\(df/dx\), que es
\[lim_{Δx \rightarrow 0} \frac{f(x) − f(x − Δx)}{Δx}, \label{3.16} \]
con la pendiente secante\(f(x)/x\) se debe a dos aproximaciones. La primera aproximación es tomar\(Δx = x\) más que\(Δx = 0\). Entonces\(df/dx ≈ (f(x) − f(0))/x\). Esta primera aproximación produce la pendiente de la línea de (0, f (0)) a (x, f (x)). La segunda aproximación reemplaza f (0) por 0, lo que produce\(df/dx ≈ f/x\); esa relación es la pendiente de la secante de (0, 0) a (x, f (x)).
Aproximación Secante Mejorada
La segunda aproximación se fija iniciando la secante en (0, f (0)) en lugar de (0, 0).
Con ese cambio, ¿cuáles son las laderas secantes y tangentes cuando\(f(x) = x^{2} + C\)?
Llamar a la secante comenzando en (0,0) la secante de origen; llamar a la nueva secante la\(x = 0\) secante. Entonces la\(x = 0\) secante siempre tiene la mitad de la pendiente de la tangente, sin importar la constante\(C\). La aproximación\(x = 0\) secante es robusta contra no se ve afectada por la traslación vertical.
¿Qué tan robusta es la aproximación\(x = 0\) secante frente a la traslación horizontal?
Para investigar cómo maneja la\(x = 0\) secante la traslación horizontal, traduzca\(f(x) = x^{2}\) hacia la derecha por 100 para hacer\(f(x) = (x − 100)^{2}\). En el vértice de la parábola\(x = 100\), la\(x = 0\) secante, de (0, 104) a (100, 0), tiene pendiente −100; sin embargo, la tangente tiene pendiente cero. Así, la\(x = 0\) secante, aunque mejora la secante de origen, se ve afectada por la traslación horizontal.
Aproximación de cambio significativo
La derivada en sí misma no se ve afectada por la traslación horizontal y vertical, por lo que una derivada adecuadamente aproximada podría ser invariante de la traducción. Una derivada aproximada es
\[\frac{df}{dx} ≈ \frac{f(x+ Δx) - f(x)}{Δx}, \label{3.17} \]
donde no\(Δx\) es cero pero sigue siendo pequeño.
¿Qué tan pequeño debería\(Δx\) ser? ¿Es lo suficientemente\(Δx = 0.01\) pequeño?
La elección\(Δx = 0.01\) tiene dos defectos. Primero, no puede funcionar cuando x tiene dimensiones. Si x es una longitud, ¿qué longitud es lo suficientemente pequeña? \(Δx = 1 mm\)La elección es probablemente lo suficientemente pequeña para calcular derivados relacionados con el sistema solar, pero probablemente sea demasiado grande para calcular derivados relacionados con la caída de gotas de niebla. En segundo lugar, ninguna elección fija puede ser invariante a escala. Aunque\(Δx = 0.01\) produce derivados precisos cuando\(f(x) = \sin x\), falla cuando\(f(x) = \sin 1000x\), el resultado de simplemente reescalar\(x\) a\(1000x\).
Estos problemas sugieren intentar la siguiente aproximación de cambio significativo:
\[\frac{df}{dx} ∼ \frac{\text{ significant }Δf \text{ (change in f) } at x}{\text{ Δx that produces a significant Δf }} \label{3.18} \]
Debido a que el\(Δx\) aquí se define por las propiedades de la curva en el punto de interés, sin favorecer valores de coordenadas particulares o valores de\(Δx\), la aproximación es la escala y la traducción invariante.
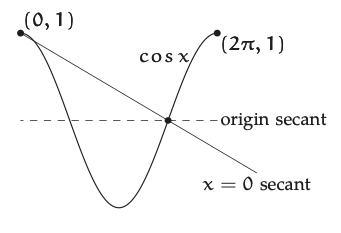
Para ilustrar esta aproximación,\(f(x) = \cos x\) intentemos estimar\(x = 3\pi/2\) con\(df/dx\) las tres aproximaciones: la secante de origen, la\(x = 0\) secante y la aproximación de cambio significativo. La secante de origen va de (0, 0) a (3\ pi/2, 0), por lo que tiene pendiente cero. Es una mala aproximación a la pendiente exacta de 1. El\(x = 0\) secante va de (0, 1) a (3\ pi/2, 0), por lo que tiene una pendiente de\(−2/3 \pi\), que es peor que predecir pendiente cero porque incluso el signo está equivocado!
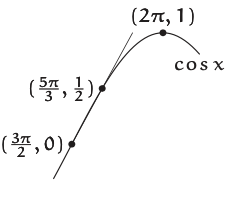
La aproximación de cambio significativo podría proporcionar más precisión. ¿En qué consiste un cambio significativo\(f(x) = \cos x\)? Debido a que el coseno cambia en 2 (de −1 a 1), llame a 1/2 un cambio significativo en\(f(x)\). Ese cambio ocurre cuando\(x\) cambia de\(3\pi/2\), dónde\(f(x) = 0\), a\(3\pi/2 + \pi/6\), dónde\(f(x) = 1/2\). En otras palabras,\(Δx\) es\(\pi/6\). Por lo tanto, la derivada aproximada es
\[\frac{df}{dx} ∼ \frac{\text{ significant Δf near x }}{Δx} ∼ \frac{1/2}{\pi/6} = \frac{3}{\pi}. \label{3.19} \]
Esta estimación es aproximadamente 0.955 sorprendentemente cercana a la verdadera derivada de 1.
Problema 3.14 Derivada de una cuadrática
Con\(f(x) = x^{2}\), estime df/dx en\(x = 5\) usando tres aproximaciones: la secante de origen, la\(x = 0\) secante y la aproximación de cambio significativo. Compara estas estimaciones con la verdadera pendiente.
Problema 3.15 Derivada del logaritmo
Utilice la aproximación de cambio significativo para estimar la derivada de\(lnx\) at\(x = 10\). Comparar la estimación con la pendiente verdadera.
Problema 3.16 Potencial Lennard—Jones
El potencial Lennard—Jones es un modelo de la energía de interacción entre dos moléculas no polares como\(N_{2}\) o\(CH_{4}\). Tiene la forma
\[V(r) = 4\mathcal{E} [ (\frac{\sigma}{r}^{12}) - (\frac{\sigma}{r}^{6})], \label{3.20} \]
donde r es la distancia entre las moléculas, y ε y σ son constantes que dependen de las moléculas. Utilizar la secante de origen para estimar\(r_{0}\), la separación\(r\) a la que\(V(r)\) es mínima. Comparar la estimación con la verdadera\(r_{0}\) encontrada usando cálculo.
Problema 3.17 Máximos y mínimos aproximados
Dejar\(f(x)\) ser una función creciente y\(g(x)\) una función decreciente. Utilizar la secante de origen para mostrar, aproximadamente, que\(h(x) = f(x) + g(x)\) tiene un mínimo donde\(f(x) = g(x)\). Esta útil regla empírica, que generaliza el Problema 3.16, a menudo se llama la heurística de equilibrio.


