7.1.1: Figuras en 1 y 2 Dimensiones

Objetivos de aprendizaje

• Identificar y definir puntos, líneas, segmentos de línea, rayos y planos.
• Clasifica los ángulos como agudos, rectos, obtusos o rectos.

Introducción

Utilizas términos geométricos en el lenguaje cotidiano, muchas veces sin pensarlo. Por ejemplo, cada vez que dices “caminar por esta línea” o “cuidado, este camino rápidamente se ángulo hacia la izquierda” estás usando términos geométricos para darle sentido al entorno que te rodea. Utiliza estos términos de manera flexible, y la gente generalmente sabe de lo que estás hablando.

En el mundo de las matemáticas, cada uno de estos términos geométricos tiene una definición específica. Es importante conocer estas definiciones, así como cómo se construyen diferentes figuras, para familiarizarse con el lenguaje de la geometría. Empecemos con una figura geométrica básica: el plano.

Figuras en un plano

Un plano es una superficie plana que continúa para siempre (o, en términos matemáticos, infinitamente) en todas las direcciones. Tiene dos dimensiones: largo y ancho.

Se puede visualizar un plano colocando un trozo de papel sobre una mesa. Ahora imagina que la hoja de papel permanece perfectamente plana y se extiende hasta donde puedes ver en dos direcciones, de izquierda a derecha y de adelante a atrás. Este gigantesco trozo de papel te da una idea de cómo es un plano geométrico: continúa infinitamente en dos direcciones. (Sin embargo, a diferencia del ejemplo de la hoja de papel, un plano geométrico no tiene altura.)

Un plano puede contener varias figuras geométricas. La idea geométrica más básica es un punto, que no tiene dimensiones. Un punto es simplemente una ubicación en el avión. Está representado por un punto. Tres puntos que no se encuentran en línea recta determinarán un plano.

La siguiente imagen muestra cuatro puntos, etiquetados A, B, C y D.

Dos puntos en un plano determinan una línea. Una línea es una figura unidimensional que se compone de un número infinito de puntos individuales colocados uno al lado del otro. En geometría, se supone que todas las líneas son rectas; si se doblan, se llaman curvas. Una línea continúa infinitamente en dos direcciones.

Abajo está la línea\(\ A B\) o, en notación geométrica,\(\ \overleftrightarrow{A B}\). Las flechas indican que la línea sigue yendo para siempre en las dos direcciones. Esta línea también podría llamarse línea\(\ BA\). Si bien el orden de los puntos no importa para una línea, es costumbre nombrar los dos puntos en orden alfabético.

La imagen de abajo muestra los puntos\(\ A\) y\(\ B\) y la línea\(\ \overleftrightarrow{A B}\).

Ejemplo

Nombra la línea que se muestra en rojo.

Solución

La línea roja pasa por los puntos\(\ C\) y\(\ F\), así es la línea\(\ \overleftrightarrow{C F}\).

\(\ \overleftrightarrow{C F}\)

Hay dos cifras más a considerar. La sección entre dos puntos cualesquiera de una línea se denomina segmento de línea. Un segmento de línea puede ser muy largo, muy corto o en algún punto intermedio. La diferencia entre una línea y un segmento de línea es que el segmento de línea tiene dos puntos finales y una línea continúa para siempre. Un segmento de línea se denota por sus dos puntos finales, como en\(\ \overline{C D}\).

Un rayo tiene un punto final y continúa para siempre en una dirección. Los matemáticos nombran un rayo con notación como\(\ \overrightarrow{E F}\), donde punto\(\ E\) es el punto final y\(\ F\) es un punto en el rayo. Al nombrar un rayo, siempre decimos primero el punto final. Tenga en cuenta que\(\ \overrightarrow{F E}\) tendría el punto final en\(\ F\), y continuar a través\(\ E\), que es un rayo diferente al\(\ \overrightarrow{E F}\), que tendría un punto final en\(\ E\), y continuar a través\(\ F\).

El término “ray” puede ser familiar porque es una palabra común en inglés. A menudo se usa “Ray” cuando se habla de luz. Si bien un rayo de luz se asemeja al término geométrico “rayo”, no continúa para siempre, y tiene algo de ancho. Un rayo geométrico no tiene ancho; solo largo.

A continuación se muestra una imagen de rayo\(\ E F\) o\(\ \overrightarrow{E F}\). Observe que el punto final es\(\ E\).

Ejemplo

Identifique cada línea y segmento de línea en la imagen de abajo.

Solución

Dos puntos definen una línea, y una línea se denota con flechas. Hay dos líneas en esta imagen:\(\ \overleftrightarrow{C E}\) y\(\ \overleftrightarrow{B G}\). Un segmento de línea es una sección entre dos puntos. \(\ \overline{D F}\)es un segmento de línea. Pero también hay dos segmentos de línea más en las propias líneas:\(\ \overline{C E}\) y\(\ \overline{B G}\).

Líneas:\(\ \overleftrightarrow{C E}, \overleftrightarrow{B G}\)

Segmentos de línea:\(\ \overline{D F}, \overline{C E}, \overline{B G}\)

Ejemplo

Identifica cada punto y rayo en la imagen de abajo.

Solución

Hay cuatro puntos:\(\ A, B, C \text{ and } D\). También hay tres rayos, aunque sólo uno puede ser obvio. Ray\(\ \overrightarrow{B C}\) comienza en el punto\( B\) y pasa por\(\ C\). Dos rayos más existen en línea\(\ \overrightarrow{A D}\): son\(\ \overrightarrow{D A}\) y\(\ \overrightarrow{A D}\).

Puntos:\(\ A, B, C, D\)

Rayos:\(\ \overrightarrow{B C}, \overrightarrow{A D}, \overrightarrow{D A}\)

Ejercicio

¿Cuál de los siguientes no está representado en la imagen de abajo?

1. \(\ \overleftrightarrow{B G}\)
2. \(\ \overrightarrow{B A}\)
3. \(\ \overline{D F}\)
4. \(\ \overrightarrow{A C}\)

Contestar

1. Incorrecto. Una línea pasa por puntos\(\ B\) y\(\ G\), así\(\ \overleftrightarrow{B G}\) se muestra. \(\ \overleftrightarrow{B A}\), no se muestra en esta imagen.
2. Correcto. Esta imagen no muestra ningún rayo que comience en el punto\(\ B\) y pase por el punto\(\ A\).
3. Incorrecto. Hay un segmento de línea que conecta puntos\(\ D\) y\(\ F\), así\(\ \overleftrightarrow{D F}\) se muestra. \(\ \overleftrightarrow{B A}\), no se muestra en esta imagen.
4. Incorrecto. Hay un rayo comenzando en punto\(\ A\) y pasando por punto\(\ C\), así\(\ \overrightarrow{A C}\) se muestra. \(\ \overrightarrow{B A}\), no se muestra en esta imagen.

Ángulos

Las líneas, los segmentos de línea, los puntos y los rayos son los bloques de construcción de otras figuras. Por ejemplo, dos rayos con un punto final común conforman un ángulo. El punto final común del ángulo se llama vértice.

El ángulo\(\ A B C\) se muestra a continuación. Este ángulo también se puede llamar\(\ \angle A B C\),\(\ \angle C B A\), o simplemente\(\ \angle B\). Cuando esté nombrando ángulos, tenga cuidado de incluir el vértice (aquí, apunte\(\ B\) como la letra media.

La imagen de abajo muestra algunos ángulos en un plano. Observe que la etiqueta de cada ángulo está escrita “punto-vértice-punto”, y la notación geométrica está en la forma\(\ \angle A B C\).

A veces los ángulos son muy estrechos; a veces son muy anchos. Cuando la gente habla del “tamaño” de un ángulo, se refiere al arco entre los dos rayos. La longitud de los rayos no tiene nada que ver con el tamaño del propio ángulo. Los dibujos de ángulos a menudo incluirán un arco (como se muestra arriba) para ayudar al lector a identificar el 'lado' correcto del ángulo.

Piensa en una cara de reloj analógico. Las manecillas de minutos y horas están ambas fijas en un punto en la mitad del reloj. A medida que pasa el tiempo, las manecillas giran alrededor del punto fijo, haciendo ángulos cada vez más grandes a medida que avanzan. La longitud de las manecillas no impacta en el ángulo que hacen las manos.

Un ángulo se mide en grados, representado por el símbolo de grado, que es un círculo pequeño en la parte superior derecha de un número. Por ejemplo, un círculo se define como tener 360 ^o. (En skateboarding y básquetbol, “hacer un 360" se refiere a saltar y hacer una rotación completa del cuerpo).

Un ángulo recto es cualquier grado que mida exactamente 90 ^o. Esto representa exactamente una cuarta parte del recorrido alrededor de un círculo. Los rectángulos contienen exactamente cuatro ángulos rectos. A menudo se usa una marca de esquina para denotar un ángulo recto, como se muestra en ángulo recto\(\ D C B\) a continuación.

Los ángulos que están entre 0 ^o y 90 ^o (más pequeños que los ángulos rectos) se denominan ángulos agudos. Los ángulos que están entre 90 ^o y 180 ^o (mayores que los ángulos rectos y menores de 180 ^o) se denominan ángulos obtusos. Y un ángulo que mide exactamente 180 ^o se llama ángulo recto porque forma una línea recta!

Ejemplo

Etiquete cada ángulo de abajo como agudo, derecho u obtuso.

Solución

Puedes comenzar identificando cualquier ángulo recto. \(\ \angle G F I\)es un ángulo recto, como lo indica la marca de esquina en el vértice\(\ F\). Los ángulos agudos serán menores que\(\ \angle G F I\) (o menores a 90 ^o). Esto significa que\(\ \angle D A B\) y\(\ \angle M L N\) son agudos. \(\ \angle T Q S\)es mayor que \(\ \angle G F I\), por lo que es un ángulo obtuso.

\(\ \angle D A B\)y\(\ \angle M L N\) son ángulos agudos.

\(\ \angle G F I\)es un ángulo recto.

\(\ \angle T Q S\)es un ángulo obtuso.

Ejemplo

Identifica cada punto, rayo y ángulo en la siguiente figura.

Solución

	Comience por identificar cada punto de la figura. Hay 4:\(\ E, F, G, \text { and } J\).
	Ahora encuentra rayos. Un rayo comienza en un punto, y luego continúa por otro punto hacia el infinito (indicado por una flecha). Tres rayos comienzan en el punto\(\ J\):\(\ \overrightarrow{J E}\),\(\ \overrightarrow{J F}\), y\(\ \overrightarrow{J G}\). Pero también fíjense que un rayo podría comenzar en el punto\(\ F\) y pasar por\(\ J\) y\(\ G\), y otro podría comenzar en el punto\(\ G\) y pasar por\(\ J\) y\(\ F\). Estos rayos pueden ser representados por\(\ \overrightarrow{G F}\) y\(\ \overrightarrow{F G}\)
	Por último, busca ángulos. \(\ \angle E J G\)es obtuso,\(\ \angle E J F\) agudo y\(\ \angle F J G\) recto. (¡No olvides esos ángulos rectos!)
Puntos:\(\ E, F, G, J\) Rayos:\(\ \overrightarrow{J E}, \overrightarrow{J G}, \overrightarrow{J F}, \overrightarrow{G F}, \overrightarrow{F G}\) Ángulos:\(\ \angle E J G, \angle E J F, \angle F J G\)

Ejercicio

Identifica los ángulos agudos en la imagen de abajo.

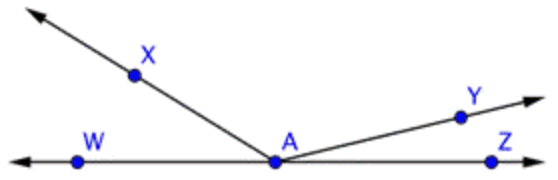
1. \(\ \angle W A X, \angle X A Y, \text { and } \angle Y A Z\)
2. \(\ \angle W A Y \text { and } \angle Y A Z\)
3. \(\ \angle W A X \text { and } \angle Y A Z\)
4. \(\ \angle W A Z \text { and } \angle X A Y\)

Contestar

1. Incorrecto. \(\ \angle W A X\)y ambos\(\ \angle Y A Z\) son ángulos agudos, pero\(\ \angle X A Y\) es un ángulo obtuso. Entonces solo\(\ \angle W A X\) y\(\ \angle Y A Z\) son ángulos agudos.
2. Incorrecto. \(\ \angle Y A Z\)es un ángulo agudo, pero\(\ \angle W A Y\) es un ángulo obtuso. Ambos\(\ \angle W A X\) y\(\ \angle Y A Z\) son ángulos agudos.
3. Correcto. Ambos\(\ \angle W A X\) y\(\ \angle Y A Z\) son ángulos agudos.
4. Incorrecto. \(\ \angle W A Z\)es un ángulo recto, y\(\ \angle X A Y\) es un ángulo obtuso. Ambos\(\ \angle W A X\) y\(\ \angle Y A Z\) son ángulos agudos.

Medición de ángulos con un Protractor

Aprender a medir ángulos puede ayudarle a sentirse más cómodo identificando la diferencia entre las mediciones de ángulo. Por ejemplo, ¿en qué se diferencia un ángulo de 135 ^o de un ángulo de 45 ^o?

La medición de ángulos requiere un transportador, que es una herramienta semicircular que contiene 180 marcas de hash individuales. Cada marca hash representa 1 ^o. (Piénsalo así: un círculo es 360 ^o, entonces un semicírculo es 180 ^o.) Para utilizar el prolongador, realice los siguientes tres pasos:

1. alinear el vértice del ángulo con el punto en el medio del lado plano (parte inferior) del transportador,
2. alinear un lado del ángulo con la línea en el transportador que está en la marca de cero grados, y
3. mira la sección curva del prolongador para leer la medición.

Actividad interactiva suplementaria

Para practicar usando un prolongador, prueba la siguiente actividad:

El siguiente ejemplo te muestra cómo usar un transportador para medir el tamaño de un ángulo.

Ejemplo

Use un prolongador para medir el ángulo que se muestra a continuación.

Solución

Usa un dispositivo de arrastre para medir el ángulo.

Alinee el punto azul del transportador con el vértice del ángulo que desea medir.

Gire el transportador alrededor del vértice del ángulo hasta que el lado del ángulo esté alineado con la marca de 0 grados del transportador.

Lee la medición, en grados, del ángulo. Comience con el lado del ángulo que esté alineado con la marca 0 ^o del transportador y cuente hacia arriba desde 0 ^o. Este ángulo mide 38 ^o.

El ángulo mide 38 ^o.

Ejercicio

¿Cuál es la medida del ángulo que se muestra a continuación?

1. 45 ^o
2. 135 ^o
3. 145 ^o
4. 180 ^o

Contestar

Resumen

Las formas geométricas y las figuras están a nuestro alrededor. Un punto es un objeto de dimensión cero que define una ubicación específica en un plano. Una línea se compone de un número infinito de puntos, todos dispuestos uno al lado del otro en un patrón recto, y continuando para siempre. Un rayo comienza en un punto y continúa hacia el infinito en una sola dirección. Un plano puede describirse como un lienzo bidimensional que dura para siempre.

Cuando dos rayos comparten un punto final, se forma un ángulo. Los ángulos pueden describirse como agudos, rectos, obtusos o rectos, y se miden en grados. Puedes usar un transportador (una herramienta matemática especial) para medir de cerca el tamaño de cualquier ángulo.