7.1.2: Propiedades de los ángulos

Objetivos de aprendizaje

• Identificar líneas paralelas y perpendiculares.
• Encuentra medidas de ángulos.
• Identificar ángulos complementarios y suplementarios.

Introducción

Imagina dos líneas separadas y distintas en un plano. Hay dos posibilidades para estas líneas: o se cruzarán en un punto, o nunca se cruzarán. Cuando dos líneas se cruzan, se forman cuatro ángulos. Entender cómo estos ángulos se relacionan entre sí puede ayudarte a averiguar cómo medirlos, incluso si solo tienes información sobre el tamaño de un ángulo.

Paralelo y perpendicular

Las líneas paralelas son dos o más líneas que nunca se cruzan. Asimismo, los segmentos de línea paralelos son dos segmentos de línea que nunca se cruzan aunque los segmentos de línea se convirtieran en líneas que continuaron para siempre. Ejemplos de segmentos de líneas paralelas están a tu alrededor, en los dos lados de esta página y en los estantes de una estantería. Cuando ves líneas o estructuras que parecen correr en la misma dirección, nunca se cruzan entre sí, y siempre están a la misma distancia, es muy probable que sean paralelas.

Las líneas perpendiculares son dos líneas que se cruzan en un ángulo de 90 ^o (recto). Y los segmentos de línea perpendiculares también se cruzan en un ángulo de 90 ^o (recto). También se pueden ver ejemplos de líneas perpendiculares en todas partes: en papel cuadriculado, en el patrón de cruce de carreteras en una intersección, hasta las líneas de colores de una camisa a cuadros. En nuestra vida cotidiana, puede estar feliz de llamar a dos líneas perpendiculares si simplemente parecen estar en ángulo recto entre sí. Sin embargo, al estudiar geometría, debe asegurarse de que dos líneas se crucen en un ángulo de 90 ^o antes de declararlas perpendiculares.

La imagen de abajo muestra algunas líneas paralelas y perpendiculares. El símbolo geométrico para paralelo es ||, así que puedes mostrarlo\(\ \overleftrightarrow{A B} \| \overleftrightarrow{C D}\). Las líneas paralelas también se indican a menudo con la marca >> en cada línea (o solo una > en cada línea). Las líneas perpendiculares se indican con el símbolo\(\ \perp\), para que puedas escribir\(\ \overleftrightarrow{W X} \perp \overleftrightarrow{Y Z}\).

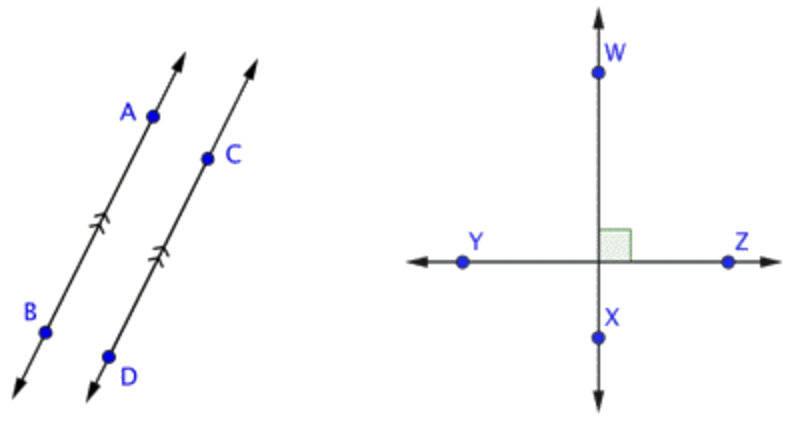
Si dos líneas son paralelas, entonces cualquier línea que sea perpendicular a una línea también será perpendicular a la otra línea. Del mismo modo, si dos líneas son ambas perpendiculares a la misma línea, entonces esas dos líneas son paralelas entre sí. Echemos un vistazo a un ejemplo e identifiquemos algunos de estos tipos de líneas.

Ejemplo

Identifica un conjunto de líneas paralelas y un conjunto de líneas perpendiculares en la imagen de abajo.

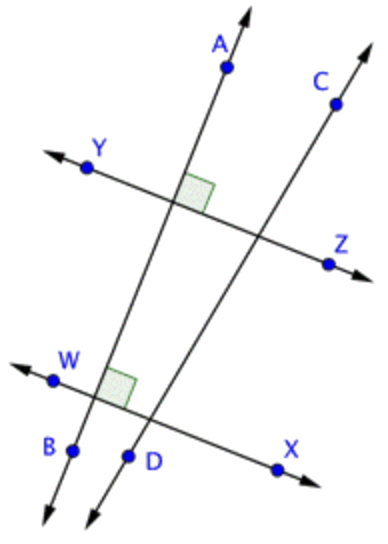
Solución

	Las líneas paralelas nunca se encuentran y las líneas perpendiculares se cruzan en ángulo recto. \(\ \overleftrightarrow{A B}\)y\(\ \overleftrightarrow{C D}\) no se crucen en esta imagen, pero si imaginas extender ambas líneas, pronto se cruzarán. Entonces, no son ni paralelos ni perpendiculares.
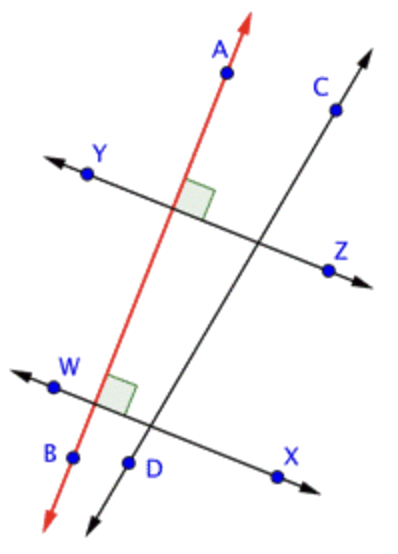	\(\ \overleftrightarrow{A B}\)es perpendicular a ambos\(\ \overleftrightarrow{W X}\) y\(\ \overleftrightarrow{Y Z}\), como lo indican las marcas de ángulo recto en la intersección de esas líneas.
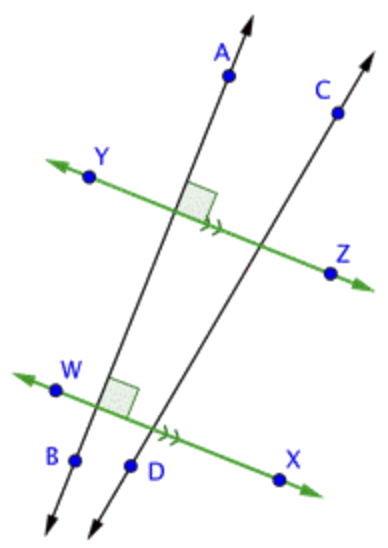	Ya que\(\ \overleftrightarrow{A B}\) es perpendicular a ambas líneas, entonces\(\ \overleftrightarrow{W X}\) y\(\ \overleftrightarrow{Y Z}\) son paralelas.

\(\ \overleftrightarrow{W X} \| \overleftrightarrow{Y Z}\)

\(\ \overleftrightarrow{A B} \perp \overleftrightarrow{W X}, \overleftrightarrow{A B} \perp \overleftrightarrow{Y Z}\)

Ejercicio

¿Qué declaración representa con mayor precisión la imagen de abajo?

1. \(\ \overleftrightarrow{E F} \| \overleftrightarrow{G H}\)
2. \(\ \overleftrightarrow{A B} \perp \overleftrightarrow{E G}\)
3. \(\ \overleftrightarrow{F H} \| \overleftrightarrow{E G}\)
4. \(\ \overleftrightarrow{A B} \| \overleftrightarrow{F H}\)

Contestar

1. Incorrecto. Esta imagen muestra las líneas\(\ \overleftrightarrow{E G}\) y\(\ \overleftrightarrow{F H}\), no\(\ \overleftrightarrow{E F}\) y\(\ \overleftrightarrow{G H}\). Ambos\(\ \overleftrightarrow{E G}\) y\(\ \overleftrightarrow{F H}\) están marcados con >> en cada línea, y esas marcas significan que son paralelas. La respuesta correcta es\(\ \overleftrightarrow{F H} \| \overleftrightarrow{E G}\).
2. Incorrecto. \(\ \overleftrightarrow{A B}\)se cruzan\(\ \overleftrightarrow{E G}\), pero la intersección no forma un ángulo recto. Esto quiere decir que no pueden ser perpendiculares. La respuesta correcta es\(\ \overleftrightarrow{F H} \| \overleftrightarrow{E G}\).
3. Correcto. Ambos\(\ \overleftrightarrow{E G}\) y\(\ \overleftrightarrow{F H}\) están marcados con >> en cada línea, y esas marcas significan que son paralelas.
4. Incorrecto. \(\ \overleftrightarrow{A B}\)y se\(\ \overleftrightarrow{F H}\) cruzan, por lo que no pueden ser paralelos. Ambos\(\ \overleftrightarrow{E G}\) y\(\ \overleftrightarrow{F H}\) están marcados con >> en cada línea, y esas marcas significan que son paralelas. La respuesta correcta es\(\ \overleftrightarrow{F H} \| \overleftrightarrow{E G}\).

Encontrar mediciones de ángulo

Entender cómo se relacionan las líneas paralelas y perpendiculares puede ayudarte a determinar las medidas de algunos ángulos desconocidos. Para comenzar, lo único que debes recordar es que las líneas perpendiculares se cruzan en un ángulo de 90 ^o, y que un ángulo recto mide 180 ^o.

La medida de un ángulo tal como\(\ \angle A\) se escribe como\(\ m \angle A\). Mira el ejemplo a continuación. ¿Cómo se pueden encontrar las medidas de los ángulos sin marcar?

Ejemplo

Encuentra la medición de\(\ \angle I J F\).

Solución

	Sólo un ángulo,\(\ \angle H J M\), está marcado en la imagen. Observe que es un ángulo recto, por lo que mide 90 ^o. \(\ \angle H J M\)está formado por la intersección de líneas\(\ \overleftrightarrow{I M}\) y\(\ \overleftrightarrow{H F}\). Ya que\(\ \overleftrightarrow{I M}\) es una línea,\(\ \angle I J M\) es un ángulo recto que mide 180 ^o.
	Puede utilizar esta información para encontrar la medición de\(\ \angle H J I\): \ (\\ comenzar {matriz} {c} m\ ángulo H J m+m\ ángulo H J I=m\ ángulo I J M\\ 90^ {\ circ} +m\ ángulo H J I=180^ {\ circ}\\ m\ ángulo H J I=90^ {\ circ} \ final {matriz}\)
	Ahora usa la misma lógica para encontrar la medición de\(\ \angle I J F\). \(\ \angle I J F\)está formado por la intersección de líneas\(\ \overleftrightarrow{I M}\) y\(\ \overleftrightarrow{H F}\). Ya que\(\ \overleftrightarrow{H F}\) es una línea,\(\ \angle H J F\) será un ángulo recto que mide 180 ^o.
	Sabes que\(\ \angle H J I\) mide 90 ^o. Utilice esta información para encontrar la medición de\(\ \angle I J F\): \ (\\ comenzar {matriz} {c} m\ ángulo H J i+m\ ángulo I J f=m\ ángulo H J F\\ 90^ {\ circ} +m\ ángulo I J F = 180^ {\ circ}\\ m\ ángulo I J F = 90^ {\ circ} \ end {array}\)

\(\ m \angle I J F=90^{\circ}\)

En este ejemplo, es posible que hayas notado que los ángulos\(\ \angle H J I, \angle I J F, \text { and } \angle H J M\) son todos ángulos rectos. (Si te pidieran encontrar la medida de\(\ \angle F J M\), encontrarías que ese ángulo es de 90 ^o, también). Esto es lo que sucede cuando dos líneas son perpendiculares: los cuatro ángulos creados por la intersección son todos ángulos rectos.

Sin embargo, no todas las intersecciones ocurren en ángulo recto. En el siguiente ejemplo, observe cómo puede usar la misma técnica que se muestra arriba (usando ángulos rectos) para encontrar la medición de un ángulo faltante.

Ejemplo

Encuentra la medición de\(\ \angle D A C\).

Solución

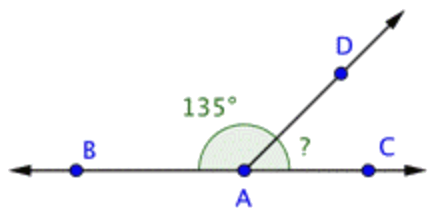	Esta imagen muestra la línea\(\ \overleftrightarrow{B C}\) y el rayo que se\(\ \overrightarrow{A D}\) cruzan en el punto\(\ A\). La medición de\(\ \angle B A D\) es de 135 ^o. Puedes usar ángulos rectos para encontrar la medición de\(\ \angle D A C\).
	\(\ \angle B A C\)es un ángulo recto, por lo que mide 180 ^o.
	Utilice esta información para encontrar la medición de\(\ \angle D A C\). \ (\\ comenzar {matriz} {c} m\ ángulo B A D+m\ ángulo D A C=m\ ángulo B A C\\ 135^ {\ circ} +m\ ángulo D A C=180^ {\ circ}\\ m\ ángulo D A C=45^ {\ circ} \ end {array}\)

\(\ m \angle D A C=45^{\circ}\)

Ejercicio

Encuentra la medición de\(\ \angle C A D\).

1. 43 ^o
2. 137 ^o
3. 147 ^o
4. 317 ^o

Contestar

Complementario y Complement

En el ejemplo anterior,\(\ m \angle B A C\) y\(\ m \angle D A C\) sumar hasta 180 ^o. Dos ángulos cuyas medidas suman 180 ^o se denominan ángulos suplementarios. También hay un término para dos ángulos cuyas medidas suman 90 ^o; se llaman ángulos complementarios.

Una forma de recordar la diferencia entre los dos términos es que “esquina” y “complementario” comienzan cada uno con c (un ángulo de 90 ^o parece una esquina), mientras que recto y “suplementario” comienzan cada uno con s (un ángulo recto mide 180 ^o).

Si puede identificar ángulos suplementarios o complementarios dentro de un problema, encontrar mediciones de ángulo faltantes suele ser simplemente una cuestión de sumar o restar.

Ejemplo

Dos ángulos son suplementarios. Si uno de los ángulos mide 48 ^o, ¿cuál es la medida del otro ángulo?

Solución

\(\ m \angle A+m \angle B=180^{\circ}\)	Dos ángulos suplementarios conforman un ángulo recto, por lo que las medidas de los dos ángulos serán de 180 ^o.
\ (\\ begin {array} {l} 48^ {\ circ} +m\ ángulo B=180^ {\ circ}\\ m\ ángulo B=180^ {\ circ} -48^ {\ circ}\\ m\ ángulo B=132^ {\ circ} \ end {array}\)	Conoces la medición de un ángulo. Para encontrar la medición del segundo ángulo, restar 48 ^o de 180 ^o.

La medida del otro ángulo es de 132 ^o.

Ejemplo

Encuentra la medición de\(\ \angle A X Z\).

Solución

	Esta imagen muestra dos líneas que se cruzan,\(\ \overleftrightarrow{A B}\) y\(\ \overleftrightarrow{Y Z}\). Se cruzan en el punto\(\ X\), formando cuatro ángulos. Los ángulos\(\ \angle A X Y\) y\(\ \angle A X Z\) son suplementarios porque juntos conforman el ángulo recto\(\ \angle Y X Z\).
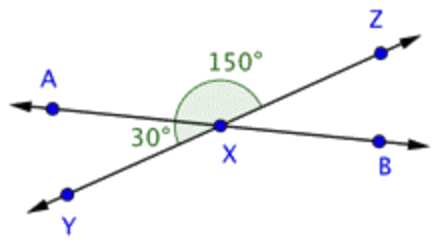	Utilice esta información para encontrar la medición de\(\ \angle A X Z\). \ (\\ comenzar {matriz} {c} m\ ángulo A X y+m\ ángulo A X z=m\ ángulo Y X Z\\ 30^ {\ circ} +m\ ángulo A X Z=180^ {\ circ}\\ m\ ángulo A X Z=150^ {\ circ} \ final {matriz}\)

\(\ m \angle A X Z=150^{\circ}\)

Ejemplo

Encuentra la medición de\(\ \angle B A C\).

Solución

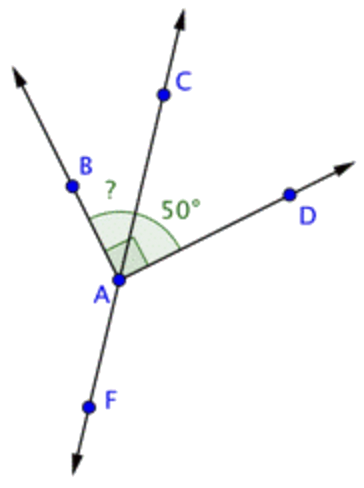	Esta imagen muestra la línea\(\ \overleftrightarrow{C F}\) y los rayos\(\ \overrightarrow{A B}\) y\(\ \overrightarrow{A D}\), todos intersectándose en el punto\(\ A\). \(\ \angle B A D\)El ángulo es un ángulo recto. Los ángulos\(\ \angle B A C\) y\(\ \angle C A D\) son complementarios, porque juntos crean\(\ \angle B A D\).
	Utilice esta información para encontrar la medición de\(\ \angle B A C\). \ (\\ comenzar {matriz} {c} m\ ángulo B A C+m\ ángulo C A D=m\ ángulo B A D\\ m\ ángulo B A C+50^ {\ circ} =90^ {\ circ}\\ m\ ángulo B A C=40^ {\ circ} \ final {matriz}\)

\(\ m \angle B A C=40^{\circ}\)

Ejemplo

Encuentra la medición de\(\ \angle C A D\).

Solución

	Ya conoces las medidas de dos ángulos aquí:\(\ \angle C A B\) y\(\ \angle D A E\). Eso también lo sabes\(\ m \angle B A E=180^{\circ}\).
	Utilice esta información para encontrar la medición de\(\ \angle C A D\). \ (\\ comenzar {matriz} {c} m\ ángulo B A C+m\ ángulo C A D+m\ ángulo D A E=m\ ángulo B A E\\ 25^ {\ circ} +m\ ángulo C A D+75^ {\ circ} =180^ {\ circ}\\ m\ ángulo C A D+100^ {\ circ} =180^ {\ circ}\\ m\ ángulo C A D=80^ {\ circ} \ end {array}\)

\(\ m \angle C A D=80^{\circ}\)

Ejercicio\(\PageIndex{1}\)

¿Qué par de ángulos es complementario?

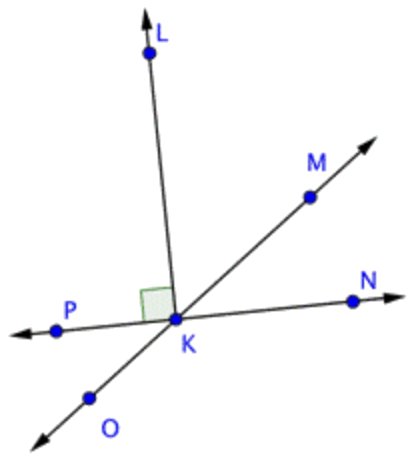
1. \(\ \angle P K O \text { and } \angle M K N\)
2. \(\ \angle P K O \text { and } \angle P K M\)
3. \(\ \angle L K P \text { and } \angle L K N\)
4. \(\ \angle L K M \text { and } \angle M K N\)

Contestar

1. Incorrecto. Las medidas de los ángulos complementarios suman 90 ^o. Parece que las medidas de estos ángulos pueden sumar hasta 90 ^o, pero no hay forma de estar seguro, por lo que no se puede decir que son complementarios. La respuesta correcta es\(\ \angle L K M \text { and } \angle M K N\).
2. Incorrecto. \(\ \angle P K O \text { and } \angle P K M\)son ángulos suplementarios (no ángulos complementarios) porque juntos comprenden el ángulo recto\(\ \angle O K M\). La respuesta correcta es\(\ \angle L K M \text { and } \angle M K N\).
3. Incorrecto. \(\ \angle L K P \text { and } \angle L K N\)son ángulos suplementarios (no ángulos complementarios) porque juntos comprenden el ángulo recto\(\ \angle P K N\). La respuesta correcta es\(\ \angle L K M \text { and } \angle M K N\).
4. Correcto. Las medidas de dos ángulos complementarios sumarán hasta 90 ^o. \(\ \angle L K P\)es un ángulo recto, por lo que también\(\ \angle L K N\) debe ser un ángulo recto. \(\ \angle L K M+\angle M K N=\angle L K N\), por lo que\(\ \angle L K M \text { and } \angle M K N\) son complementarios.

Resumen

Las líneas paralelas no se cruzan, mientras que las líneas perpendiculares se cruzan en un ángulo de 90 ^o. Se dice que dos ángulos cuyas medidas suman 180 ^o son complementarios, y dos ángulos cuyas medidas suman 90 ^o se dice que son complementarios. Para la mayoría de los pares de líneas que se cruzan, todo lo que necesita es la medición de un ángulo para encontrar las medidas de todos los demás ángulos formados por la intersección.