7.1.3: Triángulos

Objetivos de aprendizaje

• Identificar triángulos equiláteros, isósceles, escalenos, agudos, derechos y obtusos.
• Identificar si los triángulos son similares, congruentes o ninguno.
• Identificar los lados correspondientes de triángulos congruentes y similares.
• Encuentra las medidas faltantes en un par de triángulos similares.
• Resolver problemas de aplicación que involucran triángulos similares.

Introducción

Las formas geométricas, también llamadas figuras, son una parte importante del estudio de la geometría. El triángulo es una de las formas básicas en geometría. Es la forma más simple dentro de una clasificación de formas llamadas polígonos. Todos los triángulos tienen tres lados y tres ángulos, pero vienen en muchas formas y tamaños diferentes. Dentro del grupo de todos los triángulos, se utilizan las características de los lados y ángulos de un triángulo para clasificarlo aún más. Los triángulos tienen algunas características importantes, y comprender estas características permite aplicar las ideas en problemas del mundo real.

Clasificación y Nombramiento de Triángulos

Un polígono es una figura plana cerrada con tres o más lados rectos. Los polígonos tienen cada uno un nombre especial basado en el número de lados que tienen. Por ejemplo, al polígono con tres lados se le llama triángulo porque “tri” es un prefijo que significa “tres”. Su nombre también indica que este polígono tiene tres ángulos. El prefijo “poli” significa muchos.

La siguiente tabla muestra y describe tres clasificaciones de triángulos. Observe cómo se utilizan los tipos de ángulos en el triángulo para clasificar el triángulo.

Nombre del Triángulo	Imagen de Triángulo	Descripción
Triángulo Agudo		Un triángulo con 3 ángulos agudos (3 ángulos que miden entre 0 ^o y 90 ^o).
Triángulo Obtuso		Un triángulo con 1 ángulo obtuso (1 ángulo que mide entre 90 ^o y 180 ^o)
Triángulo Recto		Un triángulo que contiene un ángulo recto (1 ángulo que mide 90 ^o). Tenga en cuenta que el ángulo recto se muestra con una marca de esquina y no necesita ser etiquetado 90 ^o.

La suma de las medidas de los tres ángulos interiores de un triángulo es siempre de 180 ^o. Este hecho se puede aplicar para encontrar la medida del tercer ángulo de un triángulo, si se le dan los otros dos. Considera los ejemplos a continuación.

Ejemplo

Un triángulo tiene dos ángulos que miden 35 ^o y 75 ^o. Encuentra la medida del tercer ángulo.

Solución

\(\ 35^{\circ}+75^{\circ}+x=180^{\circ}\)	La suma de los tres ángulos interiores de un triángulo es de 180 ^o.
\ (\\ begin {array} {l} 110^ {\ circ} +x=180^ {\ circ}\ x=180^ {\ circ} -110^ {\ circ}\ x=70^ {\ circ} \ end {array}\)	Encuentra el valor de\(\ x\).

El tercer ángulo del triángulo mide 70 ^o.

Ejemplo

Uno de los ángulos en un triángulo rectángulo mide 57 ^o. Encuentra la medida del tercer ángulo.

Solución

\(\ 57^{\circ}+90^{\circ}+x=180^{\circ}\)	La suma de los tres ángulos de un triángulo es siempre de 180 ^o. Uno de los ángulos tiene una medida de 90 ^o ya que es un triángulo rectángulo.
\ (\\ begin {array} {l} 147^ {\ circ} +x=180^ {\ circ}\\ x=180^ {\ circ} -147^ {\ circ}\ x=33^ {\ circ} \ end {array}\)	Simplificar. Encuentra el valor de\(\ x\).

El tercer ángulo del triángulo rectángulo mide 33 ^o.

Existe una convención establecida para nombrar triángulos. Las etiquetas de los vértices del triángulo, que generalmente son letras mayúsculas, se utilizan para nombrar un triángulo.

Se puede llamar a este triángulo\(\ A B C\) o\(\ \triangle A B C\) desde\(\ A\)\(\ B\),, y\(\ C\) son vértices del triángulo. Al nombrar el triángulo, puede comenzar con cualquier vértice. Entonces mantén las letras en orden a medida que recorres el polígono. El triángulo de arriba podría nombrarse de varias maneras:\(\ \triangle A B C\), o\(\ \triangle C B A\). Los lados del triángulo son segmentos de línea\(\ A B\),\(\ AC\), y\(\ CB\).

Así como los triángulos pueden clasificarse como agudos, obtusos o rectos en función de sus ángulos, también pueden clasificarse por la longitud de sus lados. Los lados de igual longitud se denominan lados congruentes. Si bien designamos un segmento que une puntos\(\ A\) y\(\ B\) por la notación\(\ \overline{A B}\), designamos la longitud de un segmento que une puntos\(\ A\) y\(\ B\) por la notación\(\ AB\) sin una barra de segmento sobre él. La longitud\(\ AB\) es un número, y el segmento\(\ \overline{A B}\) es la colección de puntos que conforman el segmento.

Los matemáticos muestran congruencia al poner un símbolo de marca hash a través de la mitad de lados de igual longitud. Si la marca hash es la misma en uno o más lados, entonces esos lados son congruentes. Si los lados tienen diferentes marcas de hash, no son congruentes. En la siguiente tabla se muestra la clasificación de los triángulos por sus longitudes laterales.

Nombre del Triángulo	Imagen de Triángulo	Descripción
Triángulo Equilátero		Un triángulo cuyos tres lados tienen la misma longitud. Estos lados de igual longitud se denominan lados congruentes.
Triángulo Isósceles		Un triángulo con exactamente dos lados congruentes.
Triángulo Escaleno		Un triángulo en el que los tres lados tienen una longitud diferente.

Para describir un triángulo aún más específicamente, se puede utilizar información tanto sobre sus lados como sobre sus ángulos. Considera este ejemplo.

Ejemplo

Clasifica el triángulo a continuación.

Solución

	Observe qué tipo de ángulos tiene el triángulo. Dado que un ángulo es un ángulo recto, este es un triángulo recto.
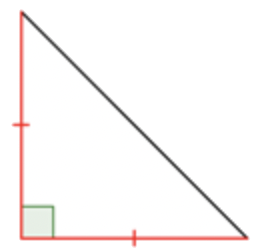	Observe las longitudes de los lados. ¿Hay marcas de congruencia u otras etiquetas? Las marcas de congruencia nos dicen que hay dos lados de igual longitud. Entonces, este es un triángulo isósceles.

Se trata de un triángulo rectángulo isósceles.

Ejercicio

Clasifica el triángulo que se muestra a continuación.

1. escaleno agudo
2. isósceles derechos
3. escaleno obtuso
4. isósceles obtusos

Contestar

1. Incorrecto. Este triángulo tiene un ángulo (ángulo\(\ Q\)) que está entre 90 ^o y 180 ^o, por lo que es un triángulo obtuso. También es escaleno porque todos los lados tienen diferentes longitudes. La respuesta correcta es obtusa escalena.
2. Incorrecto. Este triángulo no contiene un ángulo recto. Tiene un ángulo (ángulo\(\ Q\)) que está en algún lugar entre 90 ^o y 180 ^o, por lo que es un triángulo obtuso. También es escaleno porque todos los lados tienen diferentes longitudes. La respuesta correcta es obtusa escalena.
3. Correcto. Este triángulo tiene vértices\(\ P\),\(\ Q\), y\(\ R\), un ángulo (ángulo\(\ Q\)) que está entre 90 ^o y 180 ^o, y lados de tres longitudes diferentes.
4. Incorrecto. Si bien este triángulo es obtuso, no tiene dos lados de igual longitud. Sus tres lados son todos de diferentes longitudes, por lo que es escaleno. La respuesta correcta es obtusa escalena.

Identificación de triángulos congruentes y similares

Dos triángulos son congruentes si son exactamente del mismo tamaño y forma. En triángulos congruentes, las medidas de los ángulos correspondientes y las longitudes de los lados correspondientes son iguales. Considera los dos triángulos que se muestran a continuación:

Dado que ambos\(\ \angle B\) y\(\ \angle E\) son ángulos rectos, estos triángulos son triángulos rectos. Llamemos a estos dos triángulos\(\ \triangle A B C\) y\(\ \triangle D E F\). Estos triángulos son congruentes si cada par de lados correspondientes tiene longitudes iguales y cada par de ángulos correspondientes tiene la misma medida.

Los lados correspondientes son opuestos a los ángulos correspondientes.

Una flecha de doble punta significa “corresponde a”

\ (\\ comenzar {matriz} {l}
\ ángulo B\ trightarrow izquierda\ ángulo E\
\ ángulo A\ trightarrow izquierda\ ángulo D\
\ ángulo C\ triángulo izquierdo\ ángulo F\\ overline {A B}
\ izquierdafila\ overline {D E}\ overline {D E}\
\ overline {A C}\ trightarrow izquierda\ overline D F}\\
\ overline {B C}\ left trightarrow\ overline {E F}
\ end {array}\)

\(\ \triangle A B C\)y\(\ \triangle D E F\) son triángulos congruentes ya que los lados correspondientes y los ángulos correspondientes son iguales.

Echemos un vistazo a otro par de triángulos. A continuación se presentan los triángulos\(\ \triangle A B C\) y\(\ \triangle R S T\).

Estos dos triángulos seguramente no son congruentes porque\(\ \triangle R S T\) es claramente más pequeño en tamaño que\(\ \triangle A B C\). Pero, a pesar de que no son del mismo tamaño, sí se parecen entre sí. Tienen la misma forma. Los ángulos correspondientes de estos triángulos parecen tener la misma medida exacta, y si lo hicieran serían ángulos congruentes y llamaríamos a los triángulos triángulos similares.

Los ángulos congruentes están marcados con marcas hash, al igual que los lados congruentes.

También podemos mostrar ángulos congruentes usando múltiples bandas dentro del ángulo, en lugar de múltiples marcas hash en una banda. A continuación se muestra una imagen usando múltiples bandas dentro del ángulo.

Imagen que muestra triángulos\(\ A B C\) y\(\ R S T\) usando bandas para mostrar congruencia angular.

Si los ángulos correspondientes de dos triángulos tienen las mismas medidas, se les llama triángulos similares. Este nombre tiene sentido porque tienen la misma forma, pero no necesariamente el mismo tamaño. Cuando un par de triángulos es similar, los lados correspondientes son proporcionales entre sí. Eso significa que existe un factor de escala consistente que se puede utilizar para comparar los lados correspondientes. En el ejemplo anterior, las longitudes laterales del triángulo más grande son 1.4 veces la longitud del triángulo más pequeño. Entonces, triángulos similares son proporcionales entre sí.

El hecho de que dos triángulos se vean similares no significa que sean triángulos similares en el sentido matemático de la palabra. Comprobando que los ángulos correspondientes tengan igual medida es una forma de asegurarse que los triángulos son similares.

Lados correspondientes de triángulos similares

Existe otro método para determinar la similitud de triángulos que implica comparar las proporciones de las longitudes de los lados correspondientes.

Si las relaciones de los pares de lados correspondientes son iguales, los triángulos son similares.

Considera los dos triángulos a continuación.

\(\ \triangle A B C\)no es congruente con\(\ \triangle D E F\) porque las longitudes laterales de\(\ \triangle D E F\) son más largas que las de\(\ \triangle A B C\). Entonces, ¿estos triángulos son similares? Si lo son, los lados correspondientes deben ser proporcionales.

Dado que estos triángulos están orientados de la misma manera, puedes emparejar los lados izquierdo, derecho e inferior:\(\ \overline{A B}\) y\(\ \overline{D E}\),\(\ \overline{B C}\) y\(\ \overline{E F}\),\(\ \overline{A C}\) y\(\ \overline{D E}\). (Podría haber llamado a estos los dos lados más cortos, los dos lados más largos, y los dos lados sobrantes y llegaron a las mismas proporciones). Ahora veremos las proporciones de sus longitudes.

\(\ \frac{A B}{D E}=\frac{B C}{E F}=\frac{A C}{D F}\)

Sustituyendo los valores de longitud lateral en la proporción, se ve que es cierto:

\(\ \frac{3}{9}=\frac{4}{12}=\frac{6}{18}\)

Si los lados correspondientes son proporcionales, entonces los triángulos son similares. Los triángulos\(\ A B C\) y\(\ D E F\) son similares, pero no congruentes.

Usemos esta idea de lados proporcionales correspondientes para determinar si dos triángulos más son similares.

Ejemplo

Determina si los triángulos de abajo son similares viendo si sus lados correspondientes son proporcionales.

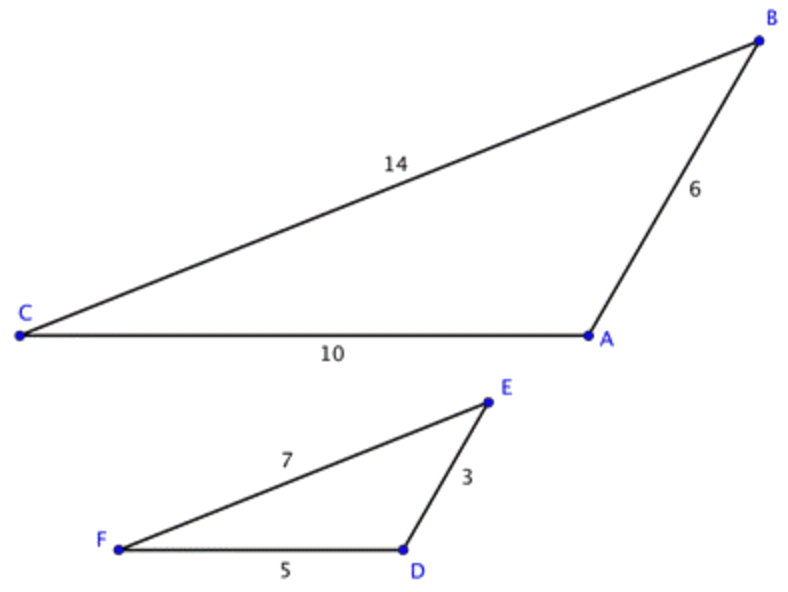
Solución

\ (\\ begin {array} {l} \ overline {C A}\ left trightarrow\ overline {F D}\ \ overline {A B}\ left trightarrow\ overline {D E}\ \ overline {B C}\ overline\ overline\ overline {E F} \ end {array}\)	Primero determinar los lados correspondientes, que son ángulos correspondientes opuestos.
\(\ \frac{C A}{F D}=\frac{A B}{D E}=\frac{B C}{E F}\)	Escribe las longitudes de lado correspondientes como proporciones.
\ (\\ begin {array} {c} \ frac {10} {5} =\ frac {6} {3} =\ frac {14} {7}\ 2=2=2 \ end {array}\)	Sustituya las longitudes de los lados en las relaciones y determine si las proporciones de los lados correspondientes son equivalentes. Lo son, por lo que los triángulos son similares.

\(\ \triangle A B C\)y\(\ \triangle D E F\) son similares.

El símbolo matemático ~ significa “es similar a”. Entonces, se puede escribir\(\ \triangle A B C\) es similar a\(\ \triangle D E F\) como\(\ \triangle A B C \sim \triangle D E F\).

Ejercicio

Determinar si los dos triángulos son similares, congruentes o ninguno.

1. \(\ \triangle A B C \text { and } \triangle D E F\)son congruentes.
2. \(\ \triangle A B C \text { and } \triangle D E F\)son similares.
3. \(\ \triangle A B C \text { and } \triangle D E F\)son similares y congruentes.
4. \(\ \triangle A B C \text { and } \triangle D E F\)no son similares ni congruentes.

Contestar

1. Incorrecto. Los triángulos congruentes tienen lados correspondientes de igual longitud y ángulos correspondientes de igual medida. Tienen el mismo tamaño y forma exactos. \(\ \triangle A B C\)es equilátero y\(\ \triangle D E F\) es isósceles, por lo que no tienen la misma forma exacta. La respuesta correcta es\(\ \triangle A B C\) y no\(\ \triangle D E F\) son similares ni congruentes.
2. Incorrecto. Las proporciones de los lados correspondientes no son iguales, por lo que los triángulos no pueden ser similares:\(\ \frac{6.5}{5}=\frac{6.5}{5} \neq \frac{5}{5}\). La respuesta correcta es\(\ \triangle A B C\) y no\(\ \triangle D E F\) son similares ni congruentes.
3. Incorrecto. Todos los triángulos congruentes son similares, pero estos triángulos no son congruentes. Los triángulos congruentes tienen lados correspondientes de igual longitud y ángulos correspondientes de igual medida. \(\ \triangle A B C\)es equilátero y\(\ \triangle D E F\) es isósceles, por lo que no tienen la misma forma exacta. La respuesta correcta es\(\ \triangle A B C\) y no\(\ \triangle D E F\) son similares ni congruentes.
4. Correcto. No se sabe que las medidas de ángulo correspondientes sean iguales como lo demuestra la ausencia de marcas de congruencia en los ángulos. Además, las proporciones de los lados correspondientes no son iguales:\(\ \frac{6.5}{5}=\frac{6.5}{5} \neq \frac{5}{5}\).

Encontrar mediciones faltantes en triángulos similares

Puedes encontrar las medidas faltantes en un triángulo si conoces algunas medidas de un triángulo similar. Veamos un ejemplo.

Ejemplo

\(\ \triangle A B C\)y\(\ \triangle X Y Z\) son triángulos similares. ¿Cuál es la longitud del lado\(\ B C\)?

Solución

\(\ \frac{B C}{Y Z}=\frac{A B}{X Y}\)	En triángulos similares, las proporciones de los lados correspondientes son proporcionales. Establecer una proporción de dos proporciones, una que incluya el lado faltante.
\(\ \frac{n}{2}=\frac{6}{1.5}\)	Sustituir en las longitudes de lado conocidas por los nombres de lado en la proporción. Deja que la longitud del lado desconocido sea\(\ n\).
\ (\\ begin {array} {r} 2\ cdot 6=1.5\ cdot n\\ 12=1.5 n\\ 8=n \ end {array}\)	Resuelve por\(\ n\) usar multiplicación cruzada.

La longitud faltante del lado\(\ BC\) es de 8 unidades.

Este proceso es bastante sencillo, pero tenga cuidado de que sus proporciones representen lados correspondientes, recordando que los lados correspondientes son ángulos correspondientes opuestos.

Solución de problemas de aplicación que involucran triángulos similares

Aplicar conocimientos de triángulos, similitud y congruencia puede ser muy útil para resolver problemas en la vida real. Así como puedes resolver las longitudes faltantes de un triángulo dibujado en una página, puedes usar triángulos para encontrar distancias desconocidas entre ubicaciones u objetos.

Consideremos el ejemplo de dos árboles y sus sombras. Supongamos que el sol está brillando sobre dos árboles, uno que mide 6 pies de altura y el otro cuya altura es desconocida. Al medir la longitud de cada sombra en el suelo, puedes usar la similitud triangular para encontrar la altura desconocida del segundo árbol.

Primero, ¡descubramos dónde están los triángulos en esta situación! Los propios árboles crean un par de lados correspondientes. Las sombras proyectadas en el suelo son otro par de lados correspondientes. El tercer lado de estos triángulos similares imaginarios va desde la parte superior de cada árbol hasta la punta de su sombra en el suelo. Esta es la hipotenusa del triángulo.

Si sabes que los árboles y sus sombras forman triángulos similares, puedes establecer una proporción para encontrar la altura del árbol.

Ejemplo

Cuando el sol está en cierto ángulo en el cielo, un árbol de 6 pies proyectará una sombra de 4 pies. ¿Qué tan alto es un árbol que proyecta una sombra de 8 pies?

Solución

\(\ \frac{\text { Tree } 1}{\text { Tree } 2}=\frac{\text { Shadow } 1}{\text { Shadow } 2}\)	Las medidas de ángulo son las mismas, por lo que los triángulos son triángulos similares. Al ser triángulos similares, puedes usar proporciones para encontrar el tamaño del lado faltante.
	Establecer una proporción comparando las alturas de los árboles y la longitud de sus sombras.
\(\ \frac{6}{h}=\frac{4}{8}\)	Sustituto en las longitudes conocidas. Llama a la altura del árbol faltante\(\ h\).
\ (\\ begin {array} {r} 6\ cdot 8=4 h\\ 48=4 h\\ 12=h \ end {array}\)	Resuelve por\(\ h\) usar multiplicación cruzada.

El árbol mide 12 pies de altura.

Resumen

Los triángulos son una de las formas básicas en el mundo real. Los triángulos se pueden clasificar por las características de sus ángulos y lados, y los triángulos se pueden comparar en función de estas características. La suma de las medidas de los ángulos interiores de cualquier triángulo es de 180 ^o. Los triángulos congruentes son triángulos del mismo tamaño y forma. Tienen lados correspondientes de igual longitud y ángulos correspondientes de la misma medida. Triángulos similares tienen la misma forma, pero no necesariamente del mismo tamaño. Las longitudes de sus lados son proporcionales. El conocimiento de los triángulos puede ser útil para resolver problemas del mundo real.