9.2.3: Restar números reales
- Page ID
- 111347
- Restar dos o más números reales.
- Simplifica las combinaciones que requieren tanto la suma como la resta de números reales.
- Resolver problemas de aplicación que requieren sustracción de números reales.
Introducción
La resta y la suma están estrechamente relacionadas. Se les llama operaciones inversas, porque una “deshace” a la otra. Entonces, al igual que con los enteros, puedes reescribir la resta como suma para restar números reales.
Inversos Aditivos
Las operaciones inversas, como la suma y la resta, son una idea clave en álgebra. Supongamos que tienes $10 y le prestas $5 a un amigo. Una hora después, ella te devuelve los 5 dólares que pidió prestados. Has vuelto a tener $10. Podrías representar la transacción así:
10-5+5=10.
Esto funciona porque un número menos en sí mismo es 0.
\(\ 3-3=0 \quad 63.5-63.5=0 \quad 39,283-39,283=0\)
Entonces, sumar un número y luego restar el mismo número es como sumar 0.
Pensando en esta idea en términos de números opuestos, también se puede decir que un número más su opuesto también es 0. Observe que cada ejemplo a continuación consiste en un par de números positivo y uno negativo sumados.
\(\ 3+(-3)=0 \quad-63.5+63.5=0 \quad 39,283+(-39,283)=0\)
Dos números son inversos aditivos si su suma es 0. Dado que esto significa que los números son opuestos (mismo valor absoluto pero signos diferentes), “inversa aditiva” es otro término, más formal para lo contrario de un número. (Tenga en cuenta que 0 es su propio inverso aditivo.)
Restar números reales
Puede usar los inversos aditivos u opuestos para reescribir la resta como suma. Si estás sumando dos números con signos diferentes, encuentras la diferencia entre sus valores absolutos y mantienes el signo del número con el mayor valor absoluto.
Cuando el número mayor es positivo, es fácil ver la conexión.
\(\ 13+(-7)=13-7\)
Ambos iguales 6.
Veamos cómo funciona esto. Cuando agregas números positivos, estás avanzando, enfrentándote en una dirección positiva.
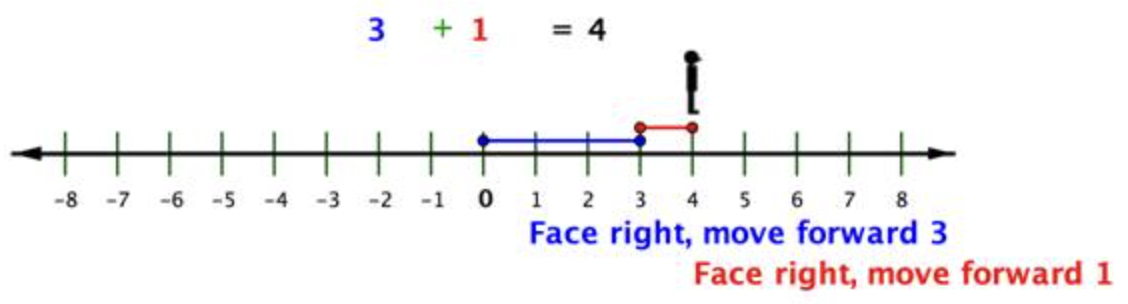
Cuando restas números positivos, puedes imaginarte moviéndote hacia atrás, pero aún enfrentándote en una dirección positiva.
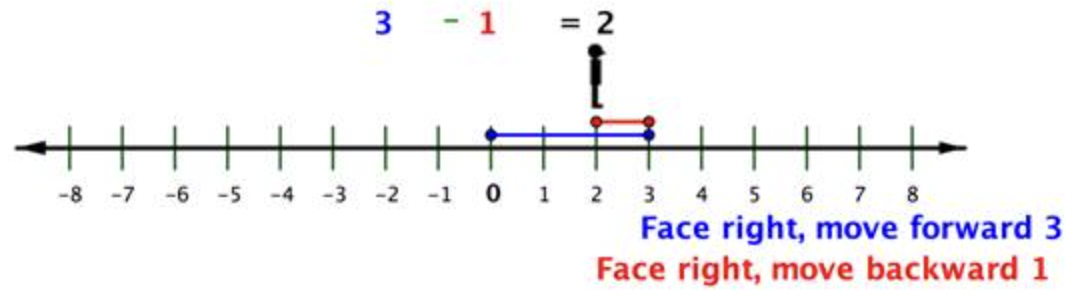
Ahora veamos qué significa esto cuando uno o más de los números son negativos.
Recordemos que cuando agregas un número negativo, avanzas, pero te enfrentas en dirección negativa (hacia la izquierda).
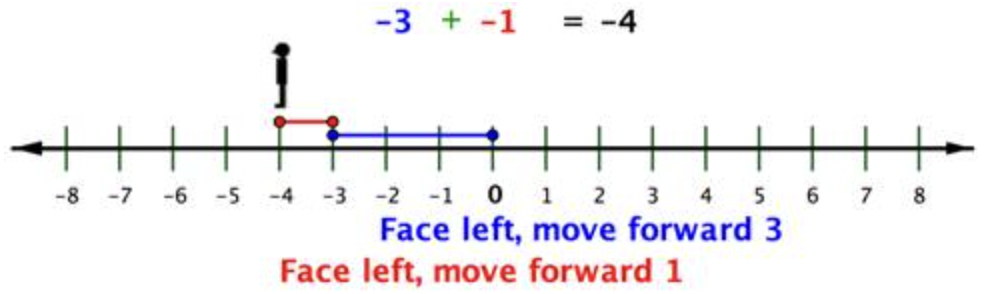
¿Cómo restas un número negativo? Primera cara y avanzar en dirección negativa al primer número, -2. Después continúe mirando en dirección negativa (hacia la izquierda), pero retroceda para restar -3.
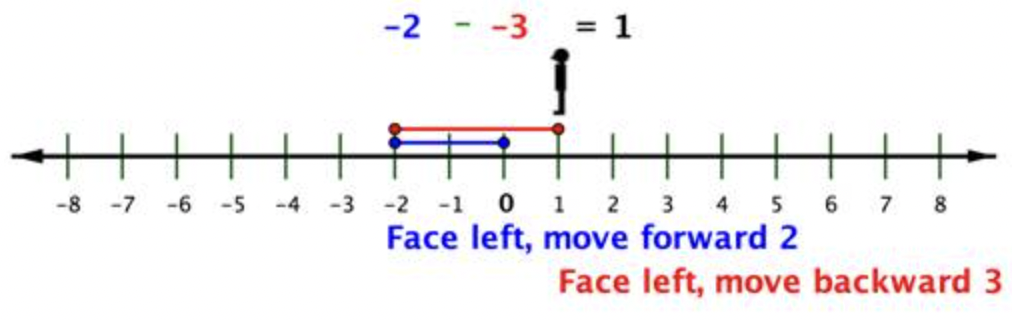
Pero, ¿no es este el mismo resultado que si hubieras sumado 3 a -2 positivos? -2+3=1.
Actividad interactiva suplementaria
Utilice la línea numérica interactiva a continuación para encontrar las respuestas a los siguientes pares de sumas y diferencias, y comparar las respuestas. Tendrás que especificar ambos números y si estás sumando o restando.
\(\ 3-4 \text { and } 3+(-4)\)
\(\ 2-(-3) \text { and } 2+3\)
\(\ -1-5 \text { and }-1+(-5)\)
\(\ -2-(-1) \text { and }-2+1\)
En cada problema de adición, te mueves en una dirección alguna distancia hacia adelante. En el problema de la resta emparejada, se mueve en dirección opuesta la misma distancia hacia atrás. ¡Observa cómo cada uno te da el mismo resultado!
Para restar un número real, se puede reescribir el problema como sumando lo contrario (inverso aditivo).
Tenga en cuenta, que si bien esto siempre funciona, la resta de números enteros sigue siendo la misma. Puedes restar 38-23 tal como siempre lo has hecho. O, también podrías reescribirlo como
38+ (-23). En ambos sentidos obtendrás la misma respuesta.
38-23=38+ (-23) =15.
Es tu elección en estos casos.
Encuentra 23-73.
Solución
| No puedes usar tu método habitual de resta, porque 73 es mayor que 23. | |
| \(\ 23+(-73)\) | Reescribe la resta como sumando lo contrario. |
| \ (\\ begin {array} {c} |23|=23\ text {y} |-73|=73\\ 73-23=50 \ end {array}\) |
Las adiciones tienen diferentes signos, así que encuentra la diferencia de sus valores absolutos. |
| \(\ 23-73=-50\) | Ya que\(\ |-73|>|23|\), la respuesta final es negativa. |
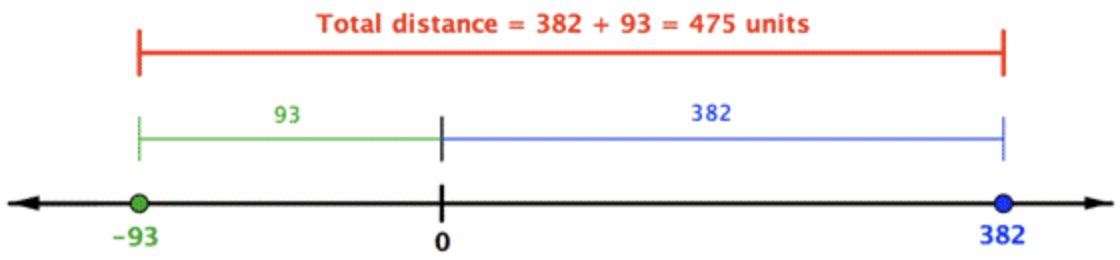
Encontrar\(\ 382-(-93)\).
Solución
|
\(\ 382+93\) \(\ 382+93=475\) |
Reescribe la resta como sumando lo contrario. Lo contrario de -93 es 93. Entonces, esto se convierte en un simple problema de adición. |
\(\ 382-(-93)=475\)
Otra forma de pensar en restar es pensar en la distancia entre los dos números en la recta numérica. En el ejemplo anterior, 382 está a la derecha de 0 por 382 unidades, y -93 está a la izquierda de 0 por 93 unidades. La distancia entre ellos es la suma de sus distancias a 0:382+93.
Encontrar\(\ 22 \frac{1}{3}-x\), cuando\(\ x=-\frac{3}{5}\).
Solución
| \(\ 22 \frac{1}{3}-\left(-\frac{3}{5}\right)\) | Sustituto\(\ -\frac{3}{5}\)\(\ x\) en la expresión. |
| \(\ 22 \frac{1}{3}+\frac{3}{5}\) | Reescribe la resta como sumando lo contrario. Lo contrario de\(\ -\frac{3}{5}\) es\(\ \frac{3}{5}\). |
|
\(\ 22 \frac{1 \cdot 5}{3 \cdot 5}+\frac{3 \cdot 3}{5 \cdot 3}=22 \frac{5}{15}+\frac{9}{15}\) \(\ 22 \frac{5}{15}+\frac{9}{15}=22 \frac{14}{15}\) |
Esto es ahora solo sumar dos números racionales. Recuerda encontrar un denominador común al sumar fracciones. 3 y 5 tienen un múltiplo común de 15; cambia los denominadores de ambas fracciones a 15 (¡y haz los cambios necesarios en el numerador!) antes de agregar. |
\(\ 22 \frac{14}{15}\)
Encontrar\(\ -32.3-(-16.3)\).
- -48.6
- -16
- 16
- 48.6
- Responder
-
- Incorrecto. Añadió -32.3 y -16.3. Para restar, cambie el problema a sumar lo contrario de -16.3, lo que da -32.3+16.3. Después usa las reglas para sumar dos números con signos diferentes. Dado que la diferencia entre 32.3 y 16.3 es 16, y |-32.3|>|16.3|, la respuesta correcta es -16.
- Correcto. Para restar, cambie el problema a sumar lo contrario de -16.3, lo que da -32.3+16.3. Después usa las reglas para sumar dos números con signos diferentes. Dado que la diferencia entre 32.3 y 16.3 es 16, y |-32.3|>|16.3|, la respuesta correcta es -16.
- Incorrecto. Usaste la señal equivocada. Para restar, cambie el problema a sumar lo contrario de -16.3, lo que da -32.3+16.3. Después usa las reglas para sumar dos números con signos diferentes. Dado que la diferencia entre 32.3 y 16.3 es 16, y |-32.3|>|16.3|, la respuesta correcta es -16.
- Incorrecto. Agregaste los opuestos de ambos números. Para restar, cambie el problema a sumar lo contrario de -16.3, lo que da -32.3+16.3. Después usa las reglas para sumar dos números con signos diferentes. Dado que la diferencia entre 32.3 y 16.3 es 16, y |-32.3|>|16.3|, la respuesta correcta es -16.
Sumando y restando más de dos números reales
Cuando tengas más de dos números reales para sumar o restar, trabaja de izquierda a derecha como lo harías al sumar más de dos números enteros. Asegúrese de cambiar la resta a la suma de lo contrario cuando sea necesario.
Encuentra -23+16- (-32) -4+6.
Solución
| \ (\\ begin {array} {r} {\ bf-23+16} - (-32) -4+6\\ {\ bf-7} - (-32) -4+6 \ end {array}\) |
Comienza con -23+16. Los agregados tienen signos diferentes, así que encuentra la diferencia y usa el signo de la adenda con el mayor valor absoluto. -23+16=-7. |
| \ (\\ begin {array} {r} {\ bf -7- (-32)} -4+6\\ {\ bf-7+32} -4+6 \ end {array}\) |
Ahora tienes -7- (-32). Reescribe esta resta como suma de lo contrario. Lo contrario de -32 es 32, por lo que esto se convierte en -7+32, lo que equivale a 25. |
| \(\ {\bf25-4}+6\) | Ahora tienes 25-4. Podrías reescribir esto como un problema de adición, pero no es necesario. |
| \(\ \bf{21}+6\) | Completar la suma final de 21+6. |
-23+16- (-32) -4+6=27
Encuentra 32- (-14) -2+ (-82).
- -66
- -38
- 98
- 126
- Responder
-
- Incorrecto. Probablemente restaste -14 incorrectamente. Para restar 32- (-14), escribe la resta como suma de lo contrario, dando 32+14=46. Después resta 2 para obtener 44, y suma -82 para obtener la respuesta correcta de -38.
- Correcto. Para restar 32- (-14), escribe la resta como suma de lo contrario, dando 32+14=46. Después resta 2 para obtener 44, y suma -82 para obtener -38.
- Incorrecto. Es posible que te hayas perdido los signos negativos en -14 y -82. Para restar 32- (-14), escribe la resta como suma de lo contrario, dando 32+14=46. Después resta 2 para obtener 44, y suma -82 para obtener la respuesta correcta de -38.
- Incorrecto. Probablemente restaste -14 correctamente, pero agregaste 82 en lugar de -82 como último paso. Para restar 32- (-14), escribe la resta como suma de lo contrario, dando 32+14=46. Después resta 2 para obtener 44, y suma -82 para obtener la respuesta correcta de -38.
Aplicaciones de la resta
Las situaciones que usan números negativos pueden requerir resta así como suma. Como viste anteriormente, a veces restar dos números positivos puede dar un resultado negativo. Debes estar seguro de que un número negativo tiene sentido en el problema.
Boston es, en promedio, 7 grados más cálido que Bangor, Maine. La baja temperatura en un día frío de invierno en Boston era de 3 o F. ¿Sobre qué baja temperatura esperarías que tuviera Bangor ese día?
Solución
| Si la temperatura en Boston es\(\ x\), la temperatura en Bangor es\(\ x-7\). | La frase “7 grados más cálidos” significa que puedes restar 7 grados de la temperatura de Boston para estimar la temperatura de Bangor. (Tenga en cuenta que también puede agregar 7 grados a la temperatura de Bangor para estimar la temperatura de Boston. ¡Ten cuidado con cuál debería tener el mayor número!) |
| \(\ x=3\) | Ese día, el mínimo de Boston fue de 3 o. |
| La temperatura de Bangor es\(\ 3-7\) | Sustituye 3 por\(\ x\) para obtener la temperatura de Bangor. |
| \(\ 3-7=3+(-7)\) | Desde 3<7, reescribe el problema de resta como suma de lo contrario. dd los números. Como uno es positivo y el otro negativo, encuentras la diferencia de |-7| y |3|, que es 4. Desde |-7|>|3|, la suma final es negativa. |
Se esperaría que la baja temperatura en Bangor, Maine sea -4 o F.
¡Everett pagó varias facturas sin balancear primero su chequera! Cuando el último cheque que escribió aún estaba por deducir de su saldo, la cuenta de Everett ya estaba sobregirada. El saldo fue de -201.35 dólares. El cheque final fue por $72.66, y otros $25 serán restados como cargo por sobregiro. ¿Cuál será el saldo de la cuenta de Everett después de ese último cheque y se deduce el cargo por sobregiro?
Solución
| \(\ -201.35-72.66-25\) | El nuevo saldo será el saldo existente de -201.35 dólares, menos el monto del cheque y el cargo por sobregiro. |
| \ (\\ begin {array} {r} -201.35-72.66-25\\ -201.35+ (-72.66) -25 \ end {array}\) |
Empezar con la primera resta,\(\ -201.35-72.66\). Reescribirlo como la adición de lo contrario de 72.66. |
| \(\ -274.01-25\) | Dado que las adiciones tienen los mismos signos, la suma es la suma de sus valores absolutos (201.35+72.66) con el mismo signo (negativo). |
| \(\ -274.01+(-25)\) | Nuevamente, reescribe la resta como la suma de lo contrario. |
| \(\ -274.01+(-25)=-299.01\) | Sumar, sumando la suma de sus valores absolutos y utilizar el mismo signo que ambas adiciones. |
El saldo de la cuenta de Everett será de -$299.01.
Un invierno, Phil voló de Siracusa, NY a Orlando, FL. La temperatura en Siracusa era de -20 o F. La temperatura en Orlando era de 75 o F. ¿Cuál fue la diferencia de temperaturas entre Siracusa y Orlando?
Solución
| \(\ 75-(-20)\) | Para encontrar la diferencia entre las temperaturas, es necesario restar. Restamos la temperatura final de la temperatura inicial para obtener el cambio de temperatura. |
| \(\ 75+20\) | Reescribe la resta como sumando lo contrario. Lo contrario de -20 es 20. |
| \(\ 75+20=95\) | Hay una diferencia de 95 grados entre 75 o y -20 o. |
La diferencia de temperaturas es de 95 grados.
Louise notó que su saldo bancario era de -$33.72 antes de que se depositara su cheque de pago. Después de que se había depositado el cheque, el saldo era de 822.98 dólares. No se realizaron otras deducciones o depósitos. ¿Cuánto dinero le pagaron?
- Responder
-
856.70$. El monto que le pagaron es la diferencia entre los dos saldos:\(\ 822.98-(-33.72)\). Esto es lo mismo que\(\ 822.98+33.72\), o 856.70.
Resumen
Restar un número es lo mismo que sumar su opuesto (también llamado su inverso aditivo). Para restar, puedes reescribir la resta como sumar lo contrario y luego usar las reglas para la suma de números reales.