9.2.4: Multiplicar y dividir números reales
- Page ID
- 111337
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Multiplica dos o más números reales.
- Simplificar mediante el uso de la propiedad de identidad de 1.
- Dividir números reales.
- Resolver problemas de aplicación que requieren multiplicación o división de números reales.
Introducción
Después de la suma y resta, las siguientes operaciones que aprendiste a hacer fueron la multiplicación y la división. Tal vez recuerdes que la multiplicación es una forma de calcular la “suma repetida”, y esto también es cierto para los números negativos.
La multiplicación y la división son operaciones inversas, así como lo son la suma y la resta. Tal vez recuerde que cuando divide fracciones, se multiplica por lo recíproco.
Multiplicar números reales
Multiplicar números reales no es tan diferente de multiplicar números enteros y fracciones positivas. Sin embargo, no has aprendido qué efecto tiene un signo negativo en el producto.
Con números enteros, se puede pensar en la multiplicación como suma repetida. Usando la línea numérica, puedes hacer múltiples saltos de un tamaño dado. Por ejemplo, la siguiente imagen muestra el producto\(\ 3 \cdot 4\) como 3 saltos de 4 unidades cada uno.
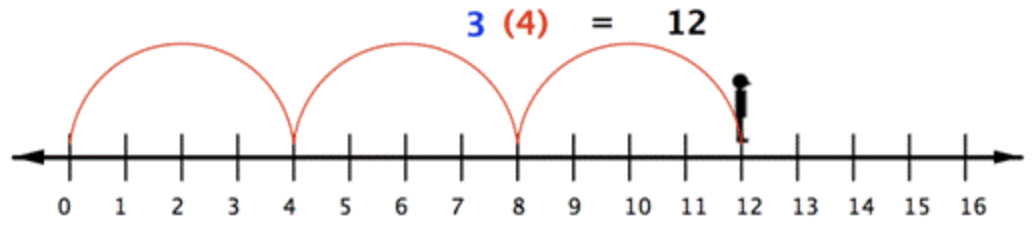
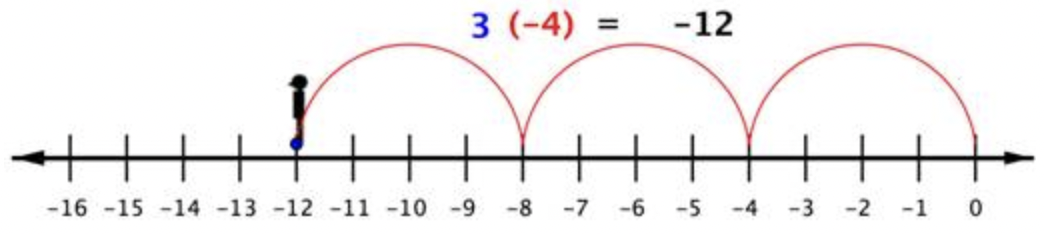
Entonces para multiplicar 3 (-4), puedes mirar hacia la izquierda (hacia el lado negativo) y hacer tres “saltos” hacia adelante (en dirección negativa).
Actividad interactiva suplementaria
Usa la línea numérica interactiva para ver cómo multiplicar enteros.
El producto de un número positivo y un número negativo (o un negativo y un positivo) es negativo. También se puede ver esto mediante el uso de patrones. En la siguiente lista de productos, el primer número es siempre 3. El segundo número disminuye en 1 con cada fila (3, 2, 1, 0, -1, -2). Busca un patrón en los productos de estos números. ¿Qué números se ajustarían al patrón de los dos últimos productos?
\ (\\ begin {array} {l}
3 (3) =9\\
3 (2) =6\\
3 (1) =3\\
3 (0) =0\\
3 (-1) =? \\
3 (-2) =?
\ end {array}\)
Observe que el patrón es el mismo si se cambia el orden de los factores:
\ (\\ begin {array} {l}
3 (3) =9\\
2 (3) =6\\
1 (3) =3\\
0 (3) =0\\
-1 (3) =? \\
-2 (3) =?
\ end {array}\)
Tómate un momento para pensar en ese patrón antes de seguir leyendo.
A medida que el factor disminuye en 1, el producto disminuye en 3. Entonces\(\ 3(-1)=-3\) y\(\ 3(-2)=-6\).
Si continúa el patrón más, verá que multiplicar 3 por un entero negativo da un número negativo. Esto es cierto en general.
Para multiplicar un número positivo y un número negativo, multiplique sus valores absolutos. El producto es negativo.
Puedes usar la idea de patrón para ver cómo multiplicar dos números negativos. Piense en cómo completaría esta lista de productos.
\ (\\ begin {array} {l}
-3 (3) =-9\\
-3 (2) =-6\\
-3 (1) =-3\\
-3 (0) =0\\
-3 (-1) =? \\
-3 (-2) =?
\ end {array}\)
A medida que el factor disminuye en 1, el producto aumenta en 3. Entonces\(\ -3(-1)=3,-3(-2)=6\).
Multiplicar -3 por un entero negativo da un número positivo. Esto es cierto en general.
Para multiplicar dos números positivos, multiplique sus valores absolutos. El producto es positivo.
Para multiplicar dos números negativos, multiplique sus valores absolutos. El producto es positivo.
Encuentra\(\ -3.8(0.6)\).
Solución
| \ (\\ begin {array} {r} 3.8\\ \ times\ quad 0.6\ \ hline 2.28 \ end {array}\) |
Multiplica los valores absolutos como lo harías normalmente. 3.8 veces 0.6. |
| Coloque el punto decimal contando los valores posicional. | |
| 3.8 tiene 1 lugar después del punto decimal, y 0.6 tiene 1 lugar después del punto decimal, por lo que el producto tiene 1+1 o 2 lugares después del punto decimal. | |
| \(\ -3.8(0.6)=-2.28\) | El producto de un negativo y un positivo es negativo. |
Encuentra\(\ \left(-\frac{3}{4}\right)\left(-\frac{2}{5}\right)\).
Solución
| \(\ \left(\frac{3}{4}\right)\left(\frac{2}{5}\right)=\frac{6}{20}=\frac{3}{10}\) |
Multiplicar los valores absolutos de los números. Primero, multiplique los numeradores juntos para obtener el numerador del producto. Después, multiplique los denominadores juntos para obtener el denominador del producto. Reescribir en los términos más bajos, si es necesario. |
| \(\ \left(-\frac{3}{4}\right)\left(-\frac{2}{5}\right)=\frac{3}{10}\) | El producto de dos números negativos es positivo. |
Encuentra\(\ 43 y\) cuándo\(\ y=-3\).
Solución
| \(\ 43(-3)\) | Sustituir -3 por\(\ y\) en la expresión. |
| \(\ 43(3)=129\) | Multiplica 43 y 3. |
| \(\ 43(-3)=-129\) | El producto de un número positivo y un número negativo es negativo. |
Para resumir:
\(\ {\bf{positive} \cdot \bf{positive}:} \text{ The product is } \bf{positive}.\)
\(\ {\bf{negative} \cdot \bf{negative}:} \text{ The product is } \bf{positive}.\)
\(\ {\bf{negative} \cdot \bf{positive}:} \text{ The product is } \bf{negative}.\)
\(\ {\bf{positive} \cdot \bf{negative}:} \text{ The product is } \bf{negative}.\)
Se puede ver que el producto de dos números negativos es un número positivo. Entonces, si estás multiplicando más de dos números, puedes contar el número de factores negativos.
Si hay un número par (0, 2, 4,...) Si hay un número par (1, 3, 5,...) de factores negativos, el producto es negativo.
Encuentra\(\ 3(-6)(2)(-3)(-1)\).
Solución
| \ (\\ begin {array} {l} {\ color {rojo} 3 (6)} (2) (3) (1)\\ {\ color {rojo} 18} {\ color {azul} (2)} (3) (1)\\ {\ color {rojo} 36} {\ color {azul} (3)} (1)\\ {\ color {rojo} 108} {\ color {azul} (1)}\\ \ color {rojo } 108 \ end {array}\) |
Multiplicar los valores absolutos de los números. |
| \(\ 3(-6)(2)(-3)(-1)\) | Contar el número de factores negativos. Hay tres (-6, -3, -1). |
| \(\ 3(-6)(2)(-3)(-1)=-108\) | Dado que hay un número impar de factores negativos, el producto es negativo. |
Encuentra\(\ (-30)(-0.5)\).
- -150
- -15
- 15
- 150
- Contestar
-
- Incorrecto. Multiplicaste 30 y 5 y olvidaste ajustar el punto decimal. También usaste el letrero equivocado. Para multiplicar 30 y 0.5, multiplicar 30 y 5 para obtener 150, luego colocar el decimal. Dado que 0.5 tiene un dígito a la derecha del punto decimal, el punto decimal en el producto necesita colocarse con un dígito a la derecha de éste para obtener 15.0, o 15. Los dos factores originales son ambos negativos. Dado que hay un número par de factores negativos, el producto es positivo. La respuesta correcta es 15.
- Incorrecto. Se multiplicó correctamente 30 y 0.5 para obtener 15, pero los dos factores originales son ambos negativos. Dado que hay un número par de factores negativos, el producto es positivo. La respuesta correcta es 15.
- Correcto. Primero, multiplica 30 y 0.5. Multiplica 30 y 5 para obtener 150, luego coloca el punto decimal. Dado que 0.5 tiene un dígito a la derecha del punto decimal, el punto decimal en el producto necesita colocarse con un dígito a la derecha de éste para obtener 15.0, o 15. Los dos factores originales son ambos negativos. Dado que hay un número par de factores negativos, el producto es positivo.
- Incorrecto. Primero, multiplica 30 y 0.5. Multiplica 30 y 5 para obtener 150, luego coloca el punto decimal. Dado que 0.5 tiene un dígito a la derecha del punto decimal, el punto decimal en el producto necesita colocarse con un dígito a la derecha de éste para obtener 15.0, o 15. Los dos factores originales son ambos negativos. Dado que hay un número par de factores negativos, el producto es positivo. La respuesta correcta es 15.
La Identidad Multiplicativa
Hay un número que se puede sumar, una y otra vez, sin cambiar nunca la suma. Ese número, 0, se llama la identidad aditiva.
También hay un número que se puede incluir como factor tantas veces como quieras, y nunca cambiará el valor del producto. Ese número, 1, se llama la identidad multiplicativa.
\ (\\ begin {array} {ll}
7 (1) =7\ quad\ quad& -7 (1) =-7\\
1 (3.6) =3.6\ quad\ quad& -\ frac {2} {23} (1) =-\ frac {2} {23}\
x (1) =x\ quad\ quad&\ text {(1)} x=x
\ end {array}\)
El patrimonio de identidad de 1 establece que\(\ x \cdot 1=x\) y\(\ 1 \cdot x=x\).
Se lo puede pensar de esta manera: Multiplicar por 1 permite que el otro número mantenga su identidad.
¿Qué es\(\ 1(y)\), cuándo\(\ y=-3\)?
- -3
- 1
- 3
- Contestar
-
- Correcto. Sustituyendo -3 por\(\ y\) da\(\ 1(-3)\), y\(\ 1(-3)=-3\).
- Incorrecto. El producto de un número y 1 es el otro número, no 1. Sustituyendo -3 por\(\ y\) da\(\ 1(-3)\), y\(\ 1(-3)=-3\).
- Incorrecto. Dice la propiedad de identidad\(\ 1 \text { . any number }=\text { that number }\). Sustituyendo -3 por\(\ y\) da\(\ 1(-3)\), y\(\ 1(-3)=-3\).
Inversaciones Multiplicativas
Se puede recordar que dos números son inversos aditivos si su suma es 0, la identidad aditiva.
3 y -3 son inversas aditivas porque\(\ 3+(-3)=0\).
Dos números son inversos multiplicativos si su producto es 1, la identidad multiplicativa.
\(\ \frac{2}{3}\)y\(\ \frac{3}{2}\) son inversos multiplicativos porque\(\ \frac{2}{3}\left(\frac{3}{2}\right)=\frac{6}{6}=1\).
Quizás recuerdes que cuando dividiste fracciones, multiplicabas por lo recíproco. Recíproco es otro nombre para el inverso multiplicativo (igual que opuesto es otro nombre para inverso aditivo).
Una manera fácil de encontrar el inverso multiplicativo es simplemente “voltear” el numerador y el denominador como lo hiciste para encontrar el recíproco. Aquí hay algunos ejemplos:
El recíproco de\(\ \frac{4}{9}\) es\(\ \frac{9}{4}\) porque\(\ \frac{4}{9}\left(\frac{9}{4}\right)=\frac{36}{36}=1\).
El recíproco de 3 es\(\ \frac{1}{3}\) porque\(\ \frac{3}{1}\left(\frac{1}{3}\right)=\frac{3}{3}=1\).
El recíproco de\(\ -\frac{5}{6}\) es\(\ -\frac{6}{5}\) porque\(\ -\frac{5}{6}\left(-\frac{6}{5}\right)=\frac{30}{30}=1\).
El recíproco de 1 es 1 as\(\ 1(1)=1\).
¿Cuál es el inverso recíproco, o multiplicativo, de -12?
- -12
- 1
- \(\ \frac{1}{12}\)
- 12
- \(\ -\frac{1}{12}\)
- Contestar
-
- Incorrecto. \(\ -12(-12)=144\), no 1. Desde\(\ -12=-\frac{12}{1}\) y\(\ -\frac{12}{1}\left(-\frac{1}{12}\right)=1\), la respuesta correcta es\(\ -\frac{1}{12}\).
- Incorrecto. El recíproco da un producto de 1; 1 es el recíproco de 1. Desde\(\ -12=-\frac{12}{1}\) y\(\ -\frac{12}{1}\left(-\frac{1}{12}\right)=1\), la respuesta correcta es\(\ -\frac{1}{12}\).
- Incorrecto. El numerador y el denominador están correctamente “volteados”, pero el signo es incorrecto. El producto necesita ser positivo 1, por lo que dado que -12 es negativo, su recíproco también debe ser negativo. Desde\(\ -12=-\frac{12}{1}\) y\(\ -\frac{12}{1}\left(-\frac{1}{12}\right)=1\), la respuesta correcta es\(\ -\frac{1}{12}\).
- Incorrecto. \(\ 12(-12)=-144\), no 1. Desde\(\ -12=-\frac{12}{1}\) y\(\ -\frac{12}{1}\left(-\frac{1}{12}\right)=1\), la respuesta correcta es\(\ -\frac{1}{12}\).
- Correcto. \(\ -12=-\frac{12}{1}\)y\(\ -\frac{12}{1}\left(-\frac{1}{12}\right)=1\).
Dividir números reales
Cuando dividiste por fracciones positivas, aprendiste a multiplicar por lo recíproco. También haces esto para dividir números reales.
Piensa en dividir una bolsa de 26 canicas en dos bolsas más pequeñas con el mismo número de canicas en cada una. También se puede decir que cada bolsa más pequeña tiene la mitad de las canicas.
\(\ 26 \div 2=26\left(\frac{1}{2}\right)=13\)
Observe que 2 y\(\ \frac{1}{2}\) son recíprocos.
Inténtalo de nuevo, dividiendo una bolsa de 36 canicas en bolsas más pequeñas.
| Cantidad de bolsas | Dividir por número de bolsas | Multiplicar por recíproco |
| \(\ 3\) | \(\ \frac{36}{3}=12\) | \(\ 36\left(\frac{1}{3}\right)=\frac{36}{3}=\frac{12(3)}{3}=12\) |
| \(\ 4\) | \(\ \frac{36}{4}=9\) | \(\ 36\left(\frac{1}{4}\right)=\frac{36}{4}=\frac{9(4)}{4}=9\) |
| \(\ 6\) | \(\ \frac{36}{6}=6\) | \(\ 36\left(\frac{1}{6}\right)=\frac{36}{6}=\frac{6(6)}{6}=6\) |
Dividir por un número es lo mismo que multiplicar por su recíproco. (Es decir, se usa el recíproco del divisor, el segundo número en el problema de división.)
Encuentra\(\ 28 \div \frac{4}{3}\).
Solución
| \(\ 28 \div \frac{4}{3}=28\left(\frac{3}{4}\right)\) | Reescribir la división como multiplicación por lo recíproco. El recíproco de\(\ \frac{4}{3}\) es\(\ \frac{3}{4}\). |
| \(\ \frac{28}{1}\left(\frac{3}{4}\right)=\frac{28(3)}{4}=\frac{4(7)(3)}{4}=7(3)=21\) | Multiplicar. |
\(\ 28 \div \frac{4}{3}=21\)
Encuentra\(\ \frac{6}{7} \div \frac{3}{10}\). Escribe la respuesta en los términos más bajos.
- \(\ \frac{9}{35}\)
- \(\ \frac{7}{20}\)
- \(\ \frac{27}{10}\)
- \(\ \frac{20}{7}\)
- Contestar
-
- Incorrecto. Multiplicaste sin antes reescribir el problema usando el recíproco. \(\ \frac{6}{7} \div \frac{3}{10}=\frac{6}{7}\left(\frac{10}{3}\right)=\frac{60}{7(3)}=\frac{20(3)}{7(3)}=\frac{20}{7}\).
- Incorrecto. Usaste el recíproco del primer número (el dividendo) en lugar del segundo número por el que estás dividiendo (el divisor). \(\ \frac{6}{7} \div \frac{3}{10}=\frac{6}{7}\left(\frac{10}{3}\right)=\frac{60}{7(3)}=\frac{20(3)}{7(3)}=\frac{20}{7}\).
- Incorrecto. Usted realizó el procedimiento de forma incorrecta. Reescribir el problema como multiplicación, utilizando el recíproco del divisor. Entonces multiplique y simplifique. \(\ \frac{6}{7} \div \frac{3}{10}=\frac{6}{7}\left(\frac{10}{3}\right)=\frac{60}{7(3)}=\frac{20(3)}{7(3)}=\frac{20}{7}\).
- Correcto. Reescribir el problema como multiplicación, utilizando el recíproco del divisor. Entonces multiplique y simplifique. \(\ \frac{6}{7} \div \frac{3}{10}=\frac{6}{7}\left(\frac{10}{3}\right)=\frac{60}{7(3)}=\frac{20(3)}{7(3)}=\frac{20}{7}\).
Ahora veamos qué significa esto cuando uno o más de los números son negativos. Un número y su recíproco tienen el mismo signo. Dado que la división se reescribe como multiplicación usando el recíproco del divisor, y tomar el recíproco no cambia ninguno de los signos, la división sigue las mismas reglas que la multiplicación.
Al dividir, reescribe el problema como multiplicación usando el recíproco del divisor como segundo factor.
Cuando un número es positivo y el otro es negativo, el cociente es negativo.
Cuando ambos números son negativos, el cociente es positivo.
Cuando ambos números son positivos, el cociente es positivo.
Encuentra\(\ 24 \div\left(-\frac{5}{6}\right)\).
Solución
| \(\ 24 \div\left(-\frac{5}{6}\right)=24\left(-\frac{6}{5}\right)\) | Reescribir la división como multiplicación por lo recíproco. |
| \(\ \frac{24}{1}\left(-\frac{6}{5}\right)=-\frac{144}{5}\) | Multiplicar. Dado que un número es positivo y uno es negativo, el producto es negativo. |
\(\ 24 \div\left(-\frac{5}{6}\right)=-\frac{144}{5}\)
Encuentra\(\ 4 x \div(-6)\) cuándo\(\ x=-\frac{2}{3}\).
Solución
| \(\ 4\left(-\frac{2}{3}\right) \div(-6)\) | Sustituto\(\ -\frac{2}{3}\)\(\ x\) en la expresión. |
| \(\ \frac{4}{1}\left(-\frac{2}{3}\right)\left(-\frac{1}{6}\right)\) | Reescribir la división como multiplicación por lo recíproco. |
| \(\ \frac{4(2)(1)}{3(6)}=\frac{8}{18}\) | Multiplicar. Hay un número par de números negativos, por lo que el producto es positivo. |
| \(\ 4 x \div(-6)=\frac{4}{9} \text { when } x=-\frac{2}{3}\) | Escribe la fracción en términos más bajos. |
Recuerda que una barra de fracción también indica división. Entonces, un signo negativo frente a una fracción va con el numerador, el denominador, o toda la fracción:\(\ -\frac{3}{4}=\frac{-3}{4}=\frac{3}{-4}\). En cada caso, la fracción general es negativa porque solo hay un negativo en la división.
Aplicaciones de Multiplicación y División
Las situaciones que requieren multiplicación o división pueden utilizar números negativos y números racionales.
Carl no sabía que su cuenta bancaria estaba exactamente a 0 cuando escribió una serie de cheques de 100 dólares. A medida que pasaba cada cheque, se cobraban 125 dólares contra su cuenta. (Además de los $100 para el cheque, hubo un cargo por sobregiro de $25). Después de 1 cheque, su cuenta era de -125 dólares. Después de 6 de estos cheques, ¿cuál era el saldo de su cuenta?
Solución
| \(\ -\$ 125(6)\) | Cada cheque reduce la cuenta en $125; esto está representado por -$125. Para encontrar la cantidad que reduce para múltiples cheques, multiplica el número de cheques por el monto cobrado. |
| \(\ -\$ 125(6)=-\$ 750\) | Multiplicar. Dado que hay un número negativo, el producto es negativo. |
El saldo de la cuenta de Carl es ahora de -750 dólares.
Brenda pensó que estaba llevando 3 barras de chocolate a un picnic con 5 amigas. Cuando sacó el chocolate, descubrió que su hermano había comido la mitad de una barra, por lo que sólo tenía\(\ 2 \frac{1}{2}\) barras para dividir entre las 6 personas (ella y sus 5 amigas). Si cada persona recibe la misma cantidad, ¿cuánto de una barra completa obtiene cada persona?
Solución
| \( 2 \frac{1}{2} \div 6\) | Dado que el caramelo se está repartido entre 6 personas, divida la cantidad de chocolate por 6. |
| \(\ 2 \frac{1}{2}\left(\frac{1}{6}\right)\) | Reescribir el problema como multiplicación, utilizando el recíproco del divisor. |
| \(\ \frac{5}{2}\left(\frac{1}{6}\right)\) | Cambiar el número mixto a una fracción impropia. Multiplicar. |
Cada persona obtiene\(\ \frac{5}{12}\) de un bar completo.
Durante una tormenta, la temperatura bajó por\(\ \frac{1}{2}\) grado cada minuto. Al inicio de la tormenta, la temperatura era de 83 o F. Una expresión que da la temperatura\(\ t\) minutos después de que comenzara la tormenta es\(\ -\frac{1}{2} t+83\). ¿Cuál era la temperatura después de 8 minutos?
Solución
| \(\ -\frac{1}{2}(8)+83\) | Sustituto 8 para\(\ t\) en la expresión. |
| \ (\\ begin {array} {l} -\ frac {1} {2}\ izquierda (\ frac {8} {1}\ derecha) +83=\\ -\ frac {8} {2} +83=-4+83 \ end {array}\) |
Primero, multiplicar. Puede resultarle útil reescribir 8 como\(\ \frac{8}{1}\) primero. Observe que ya que está multiplicando un número negativo y otro positivo, el producto es negativo. Por último, agregue. Usa las reglas para sumar números con diferentes signos. |
La temperatura fue de 79 o F después de 8 minutos.
En el transcurso de un proyecto de investigación de 18 años, la altura de un acantilado junto al mar cayó debido a la erosión del suelo. Al término de este periodo, su altura se midió como -3 pulgadas en comparación con lo que había sido al inicio del proyecto de investigación. ¿Cuál fue la cantidad promedio que la altura del acantilado cambiaba cada año?
- \(\ -6 \text { inches }\)
- \(\ -\frac{1}{6} \text { inches }\)
- \(\ \frac{1}{6} \text { inches }\)
- \(\ 6 \text { inches }\)
- Contestar
-
- Incorrecto. Dividiste el número de años por el cambio de estatura. La respuesta correcta es\(\ \frac{-3}{18}=\frac{-1}{6}=-\frac{1}{6}\) o\(\ -\frac{1}{6}\) en.
- Correcto. \(\ \frac{-3}{18}=\frac{-1}{6}=-\frac{1}{6}\)o\(\ -\frac{1}{6}\) en.
- Incorrecto. Dividiste la parte numérica correctamente, pero como estás dividiendo una altura negativa por un número positivo de años, la respuesta es negativa. La respuesta correcta es\(\ \frac{-3}{18}=\frac{-1}{6}=-\frac{1}{6}\) o\(\ -\frac{1}{6}\) en.
- Incorrecto. Dividiste el número de años por el cambio de altura y usaste el letrero equivocado. La respuesta correcta es\(\ \frac{-3}{18}=\frac{-1}{6}=-\frac{1}{6}\) o\(\ -\frac{1}{6}\) en.
Resumen
Con multiplicación y división, puedes encontrar el signo de la respuesta final contando cuántos números negativos se utilizan en el producto o cociente. Si hay un número par de negativos, el resultado es positivo. Si hay un número impar de negativos, el resultado es negativo. La división se puede reescribir como multiplicación usando el inverso recíproco o multiplicativo del divisor.