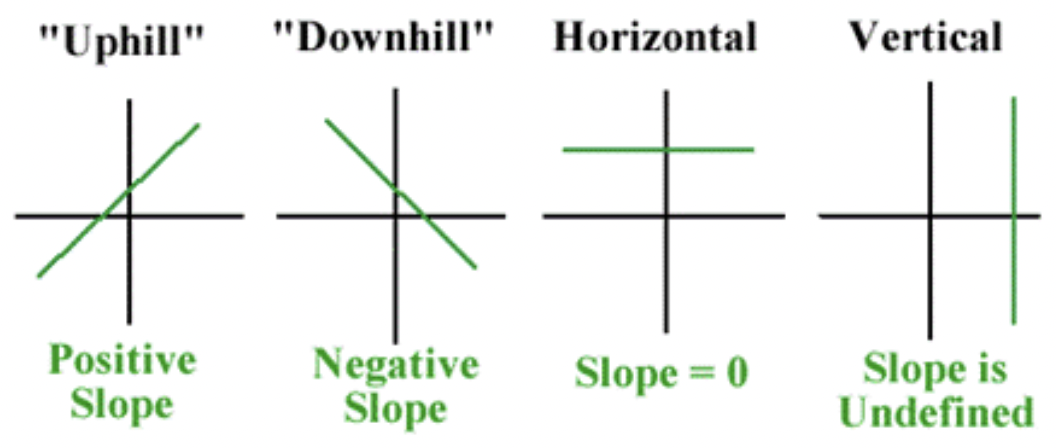
13.2.1: Encontrar la pendiente de una línea
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Encuentra la pendiente de una línea a partir de una gráfica.
- Encuentra la pendiente de una línea dada dos puntos.
- Encuentra la pendiente de las líneas x=a y y=b.
Introducción
La idea de pendiente es algo que encuentras a menudo en la vida cotidiana. Piense en rodar un carro por una rampa o subir un juego de escaleras. Tanto la rampa como las escaleras tienen pendiente. Se puede describir la pendiente, o inclinación, de la rampa y las escaleras considerando el movimiento horizontal y vertical a lo largo de ellas. En la conversación, usas palabras como “gradual” o “empinada” para describir pendiente. A lo largo de una pendiente gradual, la mayor parte del movimiento es horizontal. A lo largo de una pendiente pronunciada, el movimiento vertical es mayor.
Definición de Talud
La definición matemática de pendiente es muy similar a la nuestra cotidiana. En matemáticas, la pendiente se utiliza para describir la inclinación y dirección de las líneas. Con solo mirar la gráfica de una línea, puedes aprender algunas cosas sobre su pendiente, especialmente en relación con otras líneas gráficas en el mismo plano de coordenadas. Considere las gráficas de las tres líneas que se muestran a continuación:
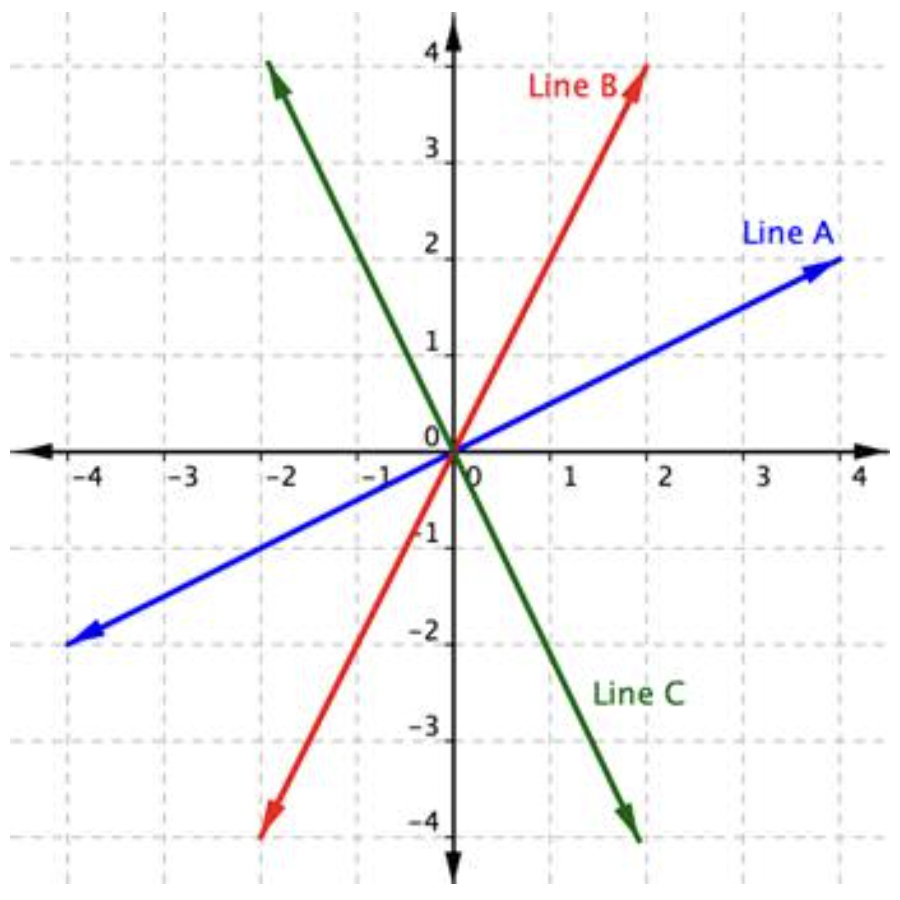
Primero, veamos las líneas A y B. Si imaginabas que estas líneas eran colinas, dirías que la línea B es más pronunciada que la línea A. La línea B tiene una pendiente mayor que la línea A.
A continuación, observe que las líneas A y B se inclinan hacia arriba a medida que se mueve de izquierda a derecha. Decimos que estas dos líneas tienen una pendiente positiva. La línea C se inclina hacia abajo de izquierda a derecha. La línea C tiene una pendiente negativa. Usando dos de los puntos de la línea, puedes encontrar la pendiente de la línea al encontrar la subida y la carrera. El cambio vertical entre dos puntos se llama subida, y el cambio horizontal se llama carrera. La pendiente es igual a la subida dividida por la carrera: Slope = rise run .
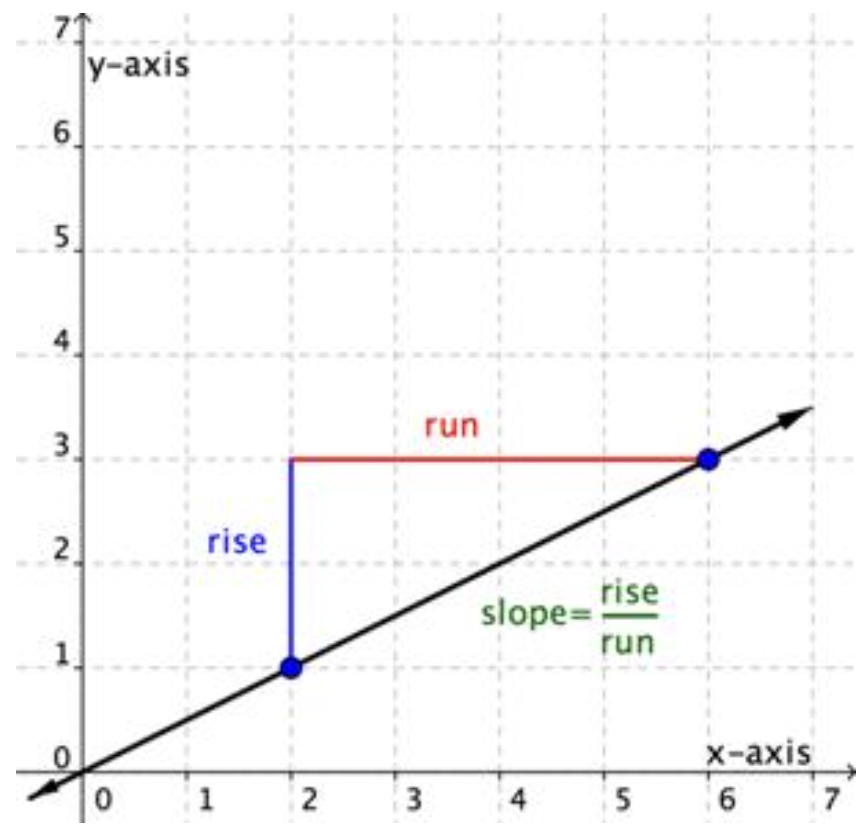
Encontrar la pendiente de una línea a partir de una gráfica
Se puede determinar la pendiente de una línea a partir de su gráfica observando el ascenso y la carrera. Una característica de una línea es que su pendiente es constante a lo largo de ella. Entonces, puedes elegir cualquier 2 puntos a lo largo de la gráfica de la línea para calcular la pendiente. Veamos un ejemplo.
Usa la gráfica para encontrar la pendiente de la línea.
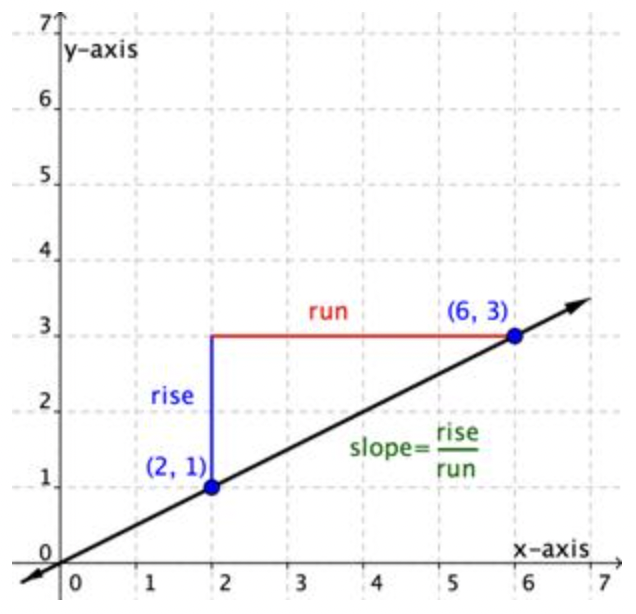
Solución
| rise =2 | Comience desde un punto de la línea, como (2, 1) y muévase verticalmente hasta que esté alineado con otro punto de la línea, como (6, 3). El ascenso es de 2 unidades. Es positivo a medida que avanzaste hacia arriba. |
| run =4 | A continuación, muévase horizontalmente hasta el punto (6, 3). Contar el número de unidades. La carrera es de 4 unidades. Es positivo ya que te mudaste a la derecha. |
| Slope =24=12 | Slope = rise run |
La pendiente es 12.
Esta línea tendrá una pendiente 12 sin importar qué dos puntos elija en la línea. Intente medir la pendiente desde el origen, (0, 0), hasta el punto (6, 3). Encontrarás que el rise =3 y el run =6. La pendiente es riserun=36=12. ¡Es lo mismo!
Veamos otro ejemplo.
Usa la gráfica para encontrar la pendiente de las dos líneas.
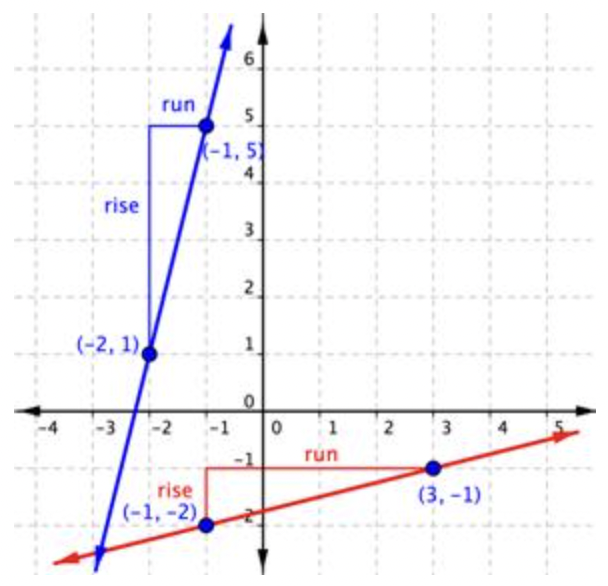
Solución
| Observe que ambas líneas tienen pendientes positivas, por lo que espera que sus respuestas sean positivas. | |
| rise =4 |
Línea azul Comienza con la línea azul, yendo del punto (-2, 1) al punto (-1, 5). Esta línea tiene una subida de 4 unidades hacia arriba, por lo que es positiva. |
| run=1 | Ejecutar es 1 unidad a la derecha, por lo que es positivo. |
| Slope =41=4 | Sustituir los valores por la subida y correr en la fórmula Slope = rise run . |
| rise =1 |
Línea roja La línea roja, que va del punto (-1, -2) al punto (3, -1) tiene una subida de 1 unidad. |
| run=4 | La línea roja tiene una tirada de 4 unidades. |
| Slope =14 | Sustituir los valores por la subida y correr hacia la fórmula Slope = rise run. |
La pendiente de la línea azul es 4 y la pendiente de la línea roja es 14.
Cuando miras las dos líneas, puedes ver que la línea azul es más pronunciada que la línea roja. Tiene sentido el valor de la pendiente de la línea azul, 4, es mayor que el valor de la pendiente de la línea roja, 14. Cuanto mayor es la pendiente, más pronunciada es la línea.
El siguiente ejemplo muestra una línea con pendiente negativa.
Encuentra la pendiente de la línea graficada a continuación.
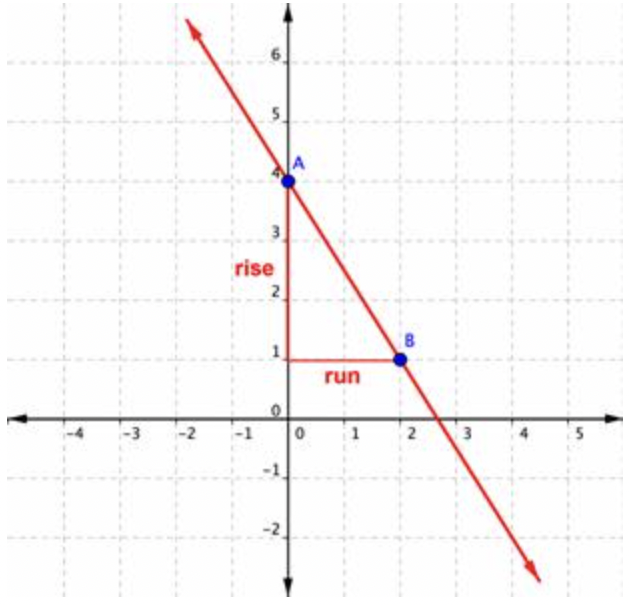
Solución
| rise =−3 | Comienza en el Punto A, (0, 4) y sube -3. Esto significa mover 3 unidades en una dirección negativa. |
| run=2 | A partir de ahí, corre 2 unidades en sentido positivo hasta el Punto B (2, 1). |
| Slope =−32 | Slope = rise run |
La pendiente de la línea es −32.
La dirección es importante a la hora de determinar pendiente. Es importante prestar atención a si se está moviendo hacia arriba, hacia abajo, hacia la izquierda o hacia la derecha; es decir, si se está moviendo en una dirección positiva o negativa. Si subes para llegar a tu segundo punto, la subida es positiva. Si bajas para llegar a tu segundo punto, la subida es negativa. Si vas a la derecha para llegar a tu segundo punto, la carrera es positiva. Si vas a la izquierda para llegar a tu segundo punto, la carrera es negativa. En el ejemplo anterior, podrías haber encontrado la pendiente iniciando en el punto B, corriendo -2, y luego subiendo +3 para llegar al punto A. El resultado sigue siendo una pendiente de riserun=+3−2=−32.
Encuentra la pendiente de la línea graficada a continuación.
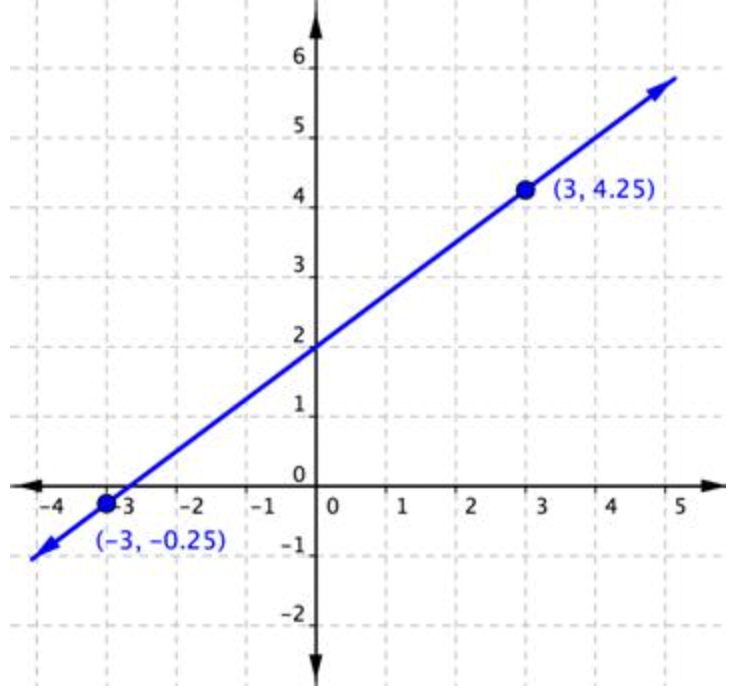
Solución
| rise=4.5 | Empezar en (-3, -0.25) y subir 4.5. Esto significa mover 4.5 unidades en una dirección positiva. |
| run=6 | De ahí, corre 6 unidades en sentido positivo a (3, 4.25). |
| Slope =4.56=0.75 | Slope = rise run |
La inclinación de la línea es 0.75.
Mirando Ecuaciones
La pendiente de una línea a veces se puede determinar rápidamente a partir de su ecuación. Consideremos la línea cuya ecuación es y=5x. Puede crear una tabla de valores para encontrar tres puntos en la línea.
| x | y |
| -1 | -5 |
| 0 | 0 |
| 2 | 10 |
Trazando estos puntos, crea la gráfica de la línea y determina la pendiente.
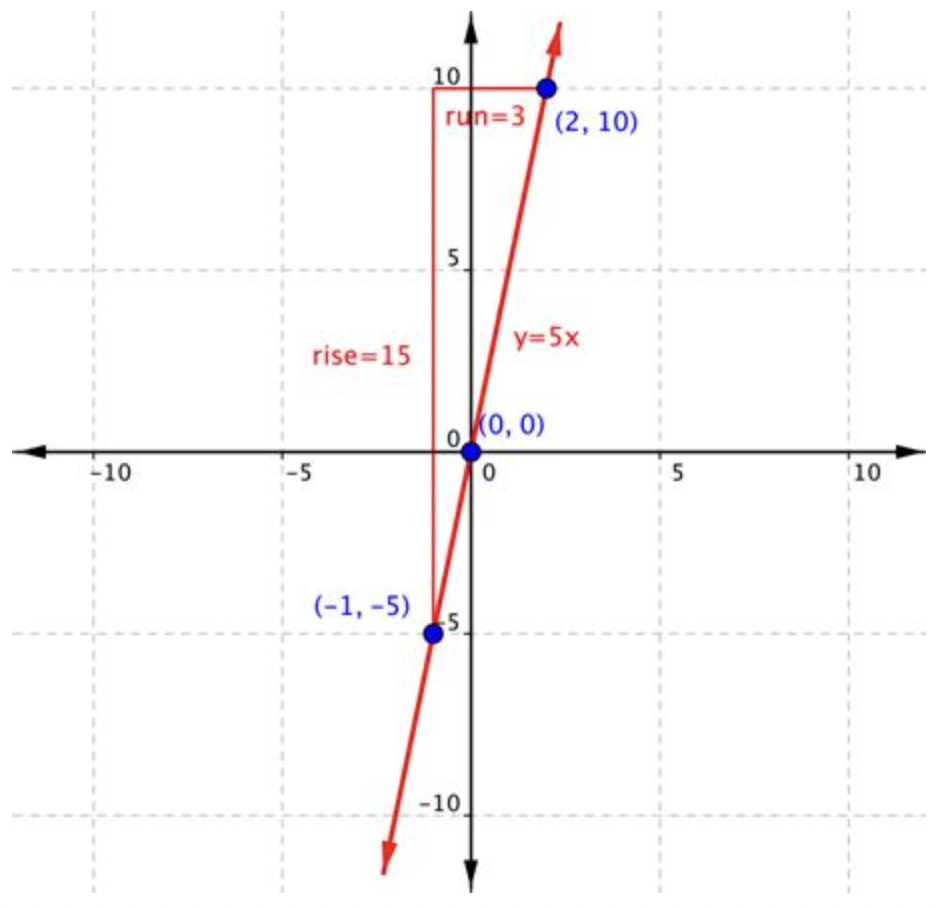
A medida que se mueve del punto (-1, -5) al punto (2, 10), la línea tiene una subida de 15 y una carrera de 3, por lo que la pendiente de la línea es 153=5. Observe que el número 5 también aparece en la ecuación: y=5x.
Siempre que la ecuación de una línea se escribe en la forma y=mx+b, se llama la forma pendiente-intercepción de la ecuación. El m es la pendiente de la línea. Y b es el b en el punto que es la intercepción y (0,b).
Por ejemplo, para la ecuación y=3x−7, la pendiente es 3, y la intercepción y es (0, -7).
¿Y si la ecuación se escribe como 2y=5x+1? Entonces debes reescribir la ecuación en la forma y=mx+b. Resolver para y.
2y=5x+1
y=52x+12dividir ambos lados de la ecuación por 2.
La pendiente es 52, y la intersección y es (0,12).
¿Cuál es la pendiente de la línea cuya ecuación es y=−2x+7?
- 7
- 2
- -2
- −72
- Contestar
-
- Incorrecto. La pendiente de una línea escrita en y=mx+b viene dada por el coeficiente de x. La respuesta correcta es -2.
- Incorrecto. La pendiente de una línea escrita en y=mx+b viene dada por el coeficiente de x. El coeficiente es -2. La respuesta correcta es -2.
- Correcto. La pendiente de una línea escrita en y=mx+b viene dada por el coeficiente de x. Para esta línea, el coeficiente, o m, la pendiente, es -2.
- Incorrecto. La pendiente de una línea escrita en y=mx+b viene dada por el coeficiente de x. El coeficiente es -2. La respuesta correcta es -2.
Encontrar la pendiente de una línea dada dos puntos
Has visto que puedes encontrar la pendiente de una línea en una gráfica midiendo la subida y la carrera. También puedes encontrar la pendiente de una línea recta sin su gráfica si conoces las coordenadas de dos puntos cualesquiera de esa línea. Cada punto tiene un conjunto de coordenadas: un valor x y un valor y, escritos como un par ordenado (x, y). El valor x te indica dónde está un punto horizontalmente. El valor y te indica dónde está el punto verticalmente.
Considera dos puntos en una línea: el punto 1 y el punto 2. El punto 1 tiene coordenadas (x1,y1) y el punto 2 tiene coordenadas (x2,y2).
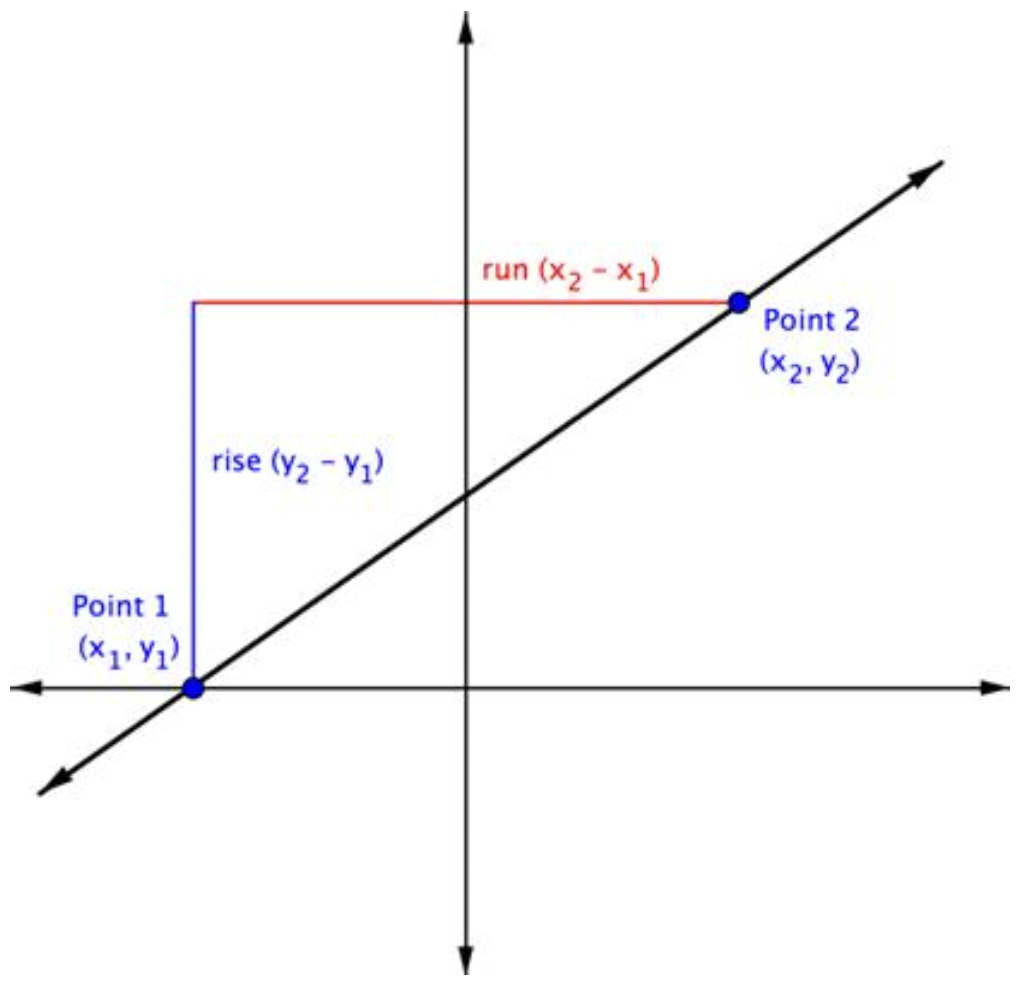
La subida es la distancia vertical entre los dos puntos, que es la diferencia entre sus coordenadas y. Eso hace que el ascenso y2−y1. La carrera entre estos dos puntos es la diferencia en las coordenadas x, o x2=x1.
Entonces, Slope = rise run o m=y2−y1x2−x1
En el siguiente ejemplo, verás que la línea tiene dos puntos cada uno indicados como un par ordenado. El punto (0, 2) se indica como Punto 1, y (-2, 6) como Punto 2. Entonces vas a moverte del Punto 1 al Punto 2. Se dibuja un triángulo encima de la línea para ayudar a ilustrar el ascenso y la carrera.
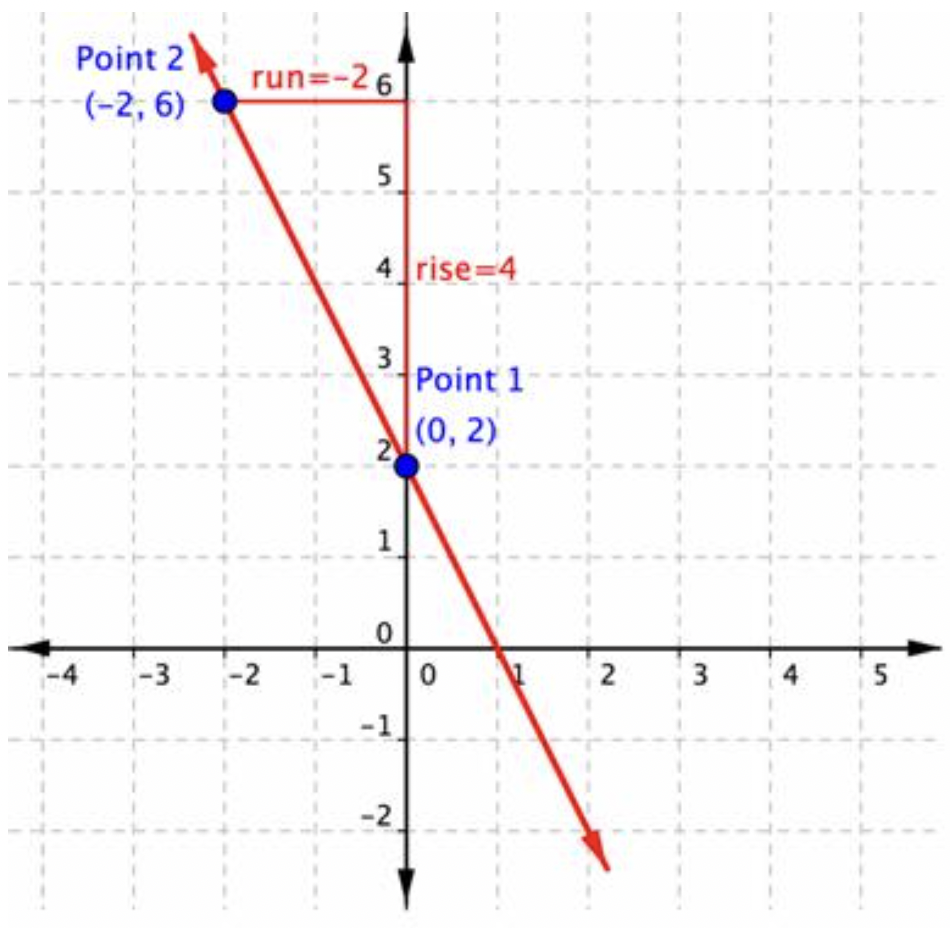
Se puede ver en la gráfica que la subida que va del Punto 1 al Punto 2 es 4, porque se están moviendo 4 unidades en una dirección positiva (hacia arriba). El recorrido es -2, porque entonces se está moviendo en dirección negativa (izquierda) 2 unidades. Usando la fórmula de pendiente, Slope =riserun=4−2=−2.
No necesitas la gráfica para encontrar la pendiente. Simplemente puedes usar las coordenadas, manteniendo un seguimiento cuidadoso de cuál es el Punto 1 y cuál es el Punto 2. Organicemos la información sobre los dos puntos:
| Nombre | Par Pedido | Coordenadas |
| Punto 1 | (0, 2) | \ (\\ begin {array} {r} x_ {1} =0\\ y_ {1} =2 \ end {array}\) |
| Punto 2 | (-2, 6) | \ (\\ comenzar {alineado} x_ {2} &=-2\\ y_ {2} &=6 \ final {alineado}\) |
La pendiente, m=y2−y1x2−x1=6−2−2−0=4−2=−2. La pendiente de la línea, m, es -2.
No importa qué punto se designe como Punto 1 y cuál es el Punto 2. Podrías haber llamado (-2, 6) Punto 1, y (0, 2) Punto 2. En ese caso, poner las coordenadas en la fórmula de pendiente produce la ecuación m=2−60−(−2)=−42=−2. Una vez más, la pendiente m=−2. Esa es la misma pendiente que antes. Lo importante es ser consistente cuando restas: siempre debes restar en el mismo orden y2−y1 y x2−x1.
¿Cuál es la pendiente de la línea que contiene los puntos (5, 5) y (4, 2)?
Solución
| \ (\\ comenzar {alineado} x_ {1} &=4\\ y_ {1} &=2 \ final {alineado}\) |
(4,2)= Point 1,(x1,y1) |
| \ (\\ comenzar {alineado} x_ {2} &=5\\ y_ {2} &=5 \ fin {alineado}\) |
(5,5)= Point 2,(x2,y2) |
| \ (\\ comenzar {alineado} m&=\ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}\\ m&=\ frac {5-2} {5-4} =\ frac {3} {1}\ m&=3 \ final {alineado}\) |
Sustituya los valores en la fórmula de pendiente y simplifique. |
El desnivel es 3.
El siguiente ejemplo muestra la solución cuando inviertes el orden de los puntos, llamando al (5, 5) al Punto 1 y al (4, 2) al Punto 2.
¿Cuál es la pendiente de la línea que contiene los puntos (5, 5) y (4, 2)?
Solución
| \ (\\ comenzar {alineado} x_ {1} &=5\\ y_ {1} &=5 \ fin {alineado}\) |
(5,5)= Point 1,(x1,y1) |
| \ (\\ comenzar {alineado} x_ {2} =4\\ y_ {2} =2 \ final {alineado}\) |
(4,2)= Point 2,(x2,y2) |
| \ (\\ comenzar {alineado} m&=\ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}\\ m&=\ frac {2-5} {4-5} =\ frac {-3} {-1} =3\\ m&=3 \ final {alineado}\) |
Sustituya los valores en la fórmula de pendiente y simplifique. |
El desnivel es 3.
Observe que independientemente de qué par ordenado se denomina Punto 1 y cuál se denomina Punto 2, la pendiente sigue siendo 3.
¿Cuál es la pendiente de la línea que contiene los puntos (3, -6.25) y (-1, 8.5)?
Solución
| \ (\\ comenzar {alineado} x_ {1} &=3\\ y_ {1} &=-6.25\\ x_ {2} &=-1\ y_ {2} &=8.5 \ end {alineado}\) |
(3,−6.25)= Point 1,(x1,y1) \ (\\ begin {array} {l} |
| \ (\\ begin {alineado} m&=\ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}\\ m&=\ frac {8.5- (-6.25)} {-1-3}\\ m&=\ frac {14.75} {-4}\ m&=-3.6875 \ end {alineado}\) |
Sustituya los valores en la fórmula de pendiente y simplifique. |
La pendiente es -3.6875.
Cuál es la pendiente de una línea que incluye los puntos (-5, 1) y (-2, 3)
- 23
- −27
- −23
- 32
- Contestar
-
- Correcto. m=3−1−2−(−5)=23
- Incorrecto. El denominador es −2−(−5), −2−5. La respuesta correcta es
- Incorrecto. Poner las coordenadas en la fórmula de pendiente consistentemente: y2−y1x2−x1. La respuesta correcta es m=3−1−2−(−5)=23.
- Incorrecto. Has intercambiado la subida y la carrera. La respuesta correcta es m=3−1−2−(−5)=23.
¿Cuál es la pendiente de una línea que incluye los puntos (5,−15) y (−3,35)?
- −10
- 825
- −120
- −110
- Contestar
-
- Incorrecto. Parece que invertiste la subida y la carrera. Usa la fórmula m=y2−y1x2−x1 para encontrar la pendiente. La respuesta correcta es −110.
- Incorrecto. Parece que restaste ya sea las x coordenadas y o en el orden equivocado. Asegúrese de restar y2=y1, entonces x2−x1, y luego calcular la pendiente. La respuesta correcta es −110.
- Incorrecto. Parece que restaste ya sea las x coordenadas y o en el orden equivocado. Asegúrese de restar y2=y1, entonces x2−x1, y luego calcular la pendiente. La respuesta correcta es −110.
- Correcto. Usando la fórmula para pendiente, m=y2−y1x2−x1, encontraste eso m=35−(−15)−3−5=45−8=45÷(−8)=45⋅1−8=−440=−110.
Encontrar las pendientes de las líneas horizontales y verticales
Hasta ahora, has considerado líneas que corren “cuesta arriba” o “cuesta abajo”. Sus pendientes pueden ser empinadas o graduales, pero siempre son números positivos o negativos. Pero hay otros dos tipos de líneas, la horizontal y la vertical. ¿Cuál es la pendiente de una línea plana o terreno nivelado? ¿De una pared o una línea vertical?
Consideremos una línea horizontal en una gráfica. No importa qué dos puntos elija en la línea, siempre tendrán la misma coordenada y. La ecuación para esta línea es y=3. La ecuación también se puede escribir como y=(0)x+3.
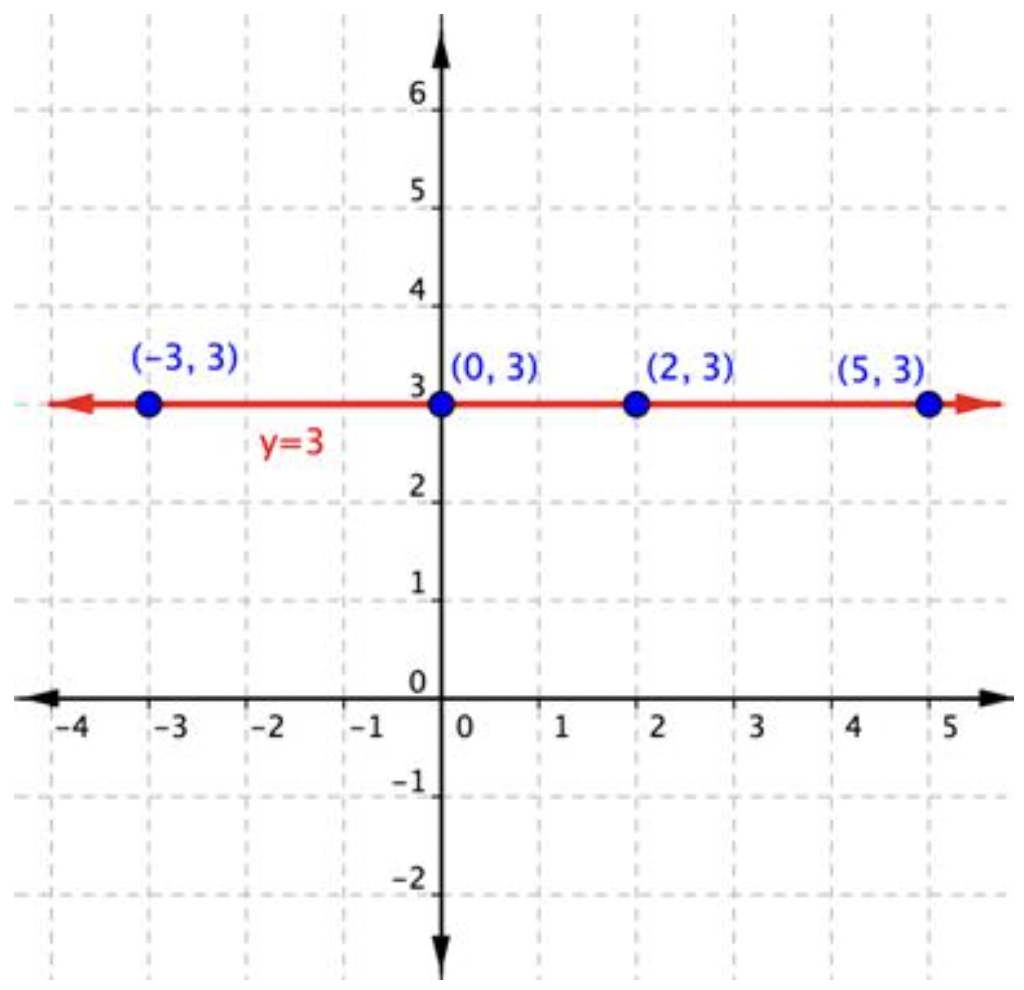
Usando el formulario y=0x+3, se puede ver que la pendiente es 0. También puede utilizar la fórmula de pendiente con dos puntos en esta línea horizontal para calcular la pendiente de esta línea horizontal. Usando (−3,3) como Punto 1 y (2,3) como Punto 2, obtienes:
\ (\\ begin {array} {c}
m=\ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}\\
m=\ frac {3-3} {2- (-3)} =\ frac {0} {5} =0
\ end {array}\)
La pendiente de esta línea horizontal es 0.
Consideremos cualquier línea horizontal. No importa qué dos puntos elija en la línea, siempre tendrán la misma coordenada y. Entonces, cuando aplicas la fórmula de pendiente, el numerador siempre será 0. El cero dividido por cualquier número distinto de cero es 0, por lo que la pendiente de cualquier línea horizontal siempre es 0.
La ecuación para la línea y=3 horizontal te dice que no importa qué dos puntos elijas en esta línea, la coordenada y siempre será 3.
¿Qué tal las líneas verticales? En su caso, no importa qué dos puntos elijas, siempre tendrán la misma coordenada x. La ecuación para esta línea es x=2.
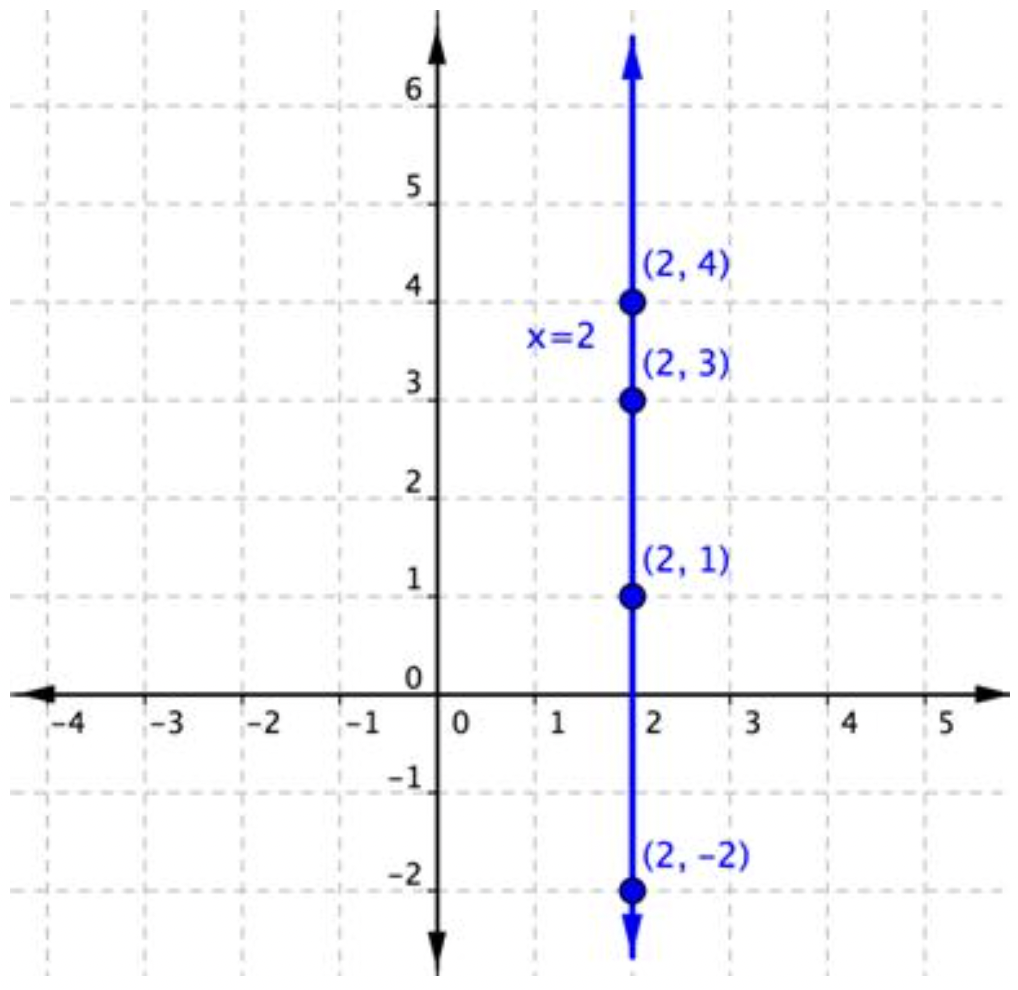
No hay manera de que esta ecuación se pueda poner en forma de pendiente-punto, ya que el coeficiente de y es 0 (x=0y+2).
Entonces, ¿qué sucede cuando se utiliza la fórmula de pendiente con dos puntos en esta línea vertical para calcular la pendiente? Usando (2,1) como Punto 1 y (2,3) como Punto 2, obtienes:
\ (\\ begin {array} {c}
m=\ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}\\
m=\ frac {3-1} {2-2} =\ frac {2} {0}
\ end {array}\)
Pero la división por cero no tiene sentido para el conjunto de números reales. Debido a este hecho, se dice que la pendiente de esta línea vertical es indefinida. Esto es cierto para todas las líneas verticales —todas tienen una pendiente que no está definida.
¿Cuál es la pendiente de la línea que contiene los puntos (3, 2) y (-8, 2)?
Solución
| \ (\\ begin {array} {l} x_ {1} =3\\ y_ {1} =2 \ end {array}\) |
(3,2)= Point 1,(x1,y1) |
| \ (\\ begin {array} {c} x_ {2} =-8\\ y_ {2} =2 \ end {array}\) |
(−8,2)= Point 2,(x2,y2) |
| \ (\\ begin {array} {r} \ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}\ \ frac {(2) - (2)} {(-8) - (3)} =\ frac {0} {-11} =0\\ m=0 \ end {array}\) |
Sustituya los valores en la fórmula de pendiente y simplifique. |
La pendiente es 0, por lo que la línea es horizontal.
¿Cuál de los siguientes puntos se ubicará en la línea creada por los puntos (−3.75,6.25) y (−3.75,0)?
- (0,−3.75)
- (−3.75,−14.55)
- (3.75,−6.25)
- (0,6.25)
- Contestar
-
- Incorrecto. Observe que ambos puntos de la línea tienen la misma coordenada x pero diferentes coordenadas y. Eso la convierte en una línea vertical, por lo que cualquier otro punto de la línea tendrá una coordenada x de -3.75. La respuesta correcta es (−3.75,−14.55).
- Correcto. Los puntos (−3.75,6.25) y (−3.75,0) forman una línea vertical, por lo que cualquier otro punto de esa línea tendrá que tener una coordenada x de -3.75.
- Incorrecto. Intenta dibujar un boceto rápido de los puntos (−3.75,6.25) y (−3.75,0). Forman una línea vertical, por lo que cualquier otro punto de la línea tendrá una coordenada x de -3.75. La respuesta correcta es (−3.75,−14.55).
- Incorrecto. Observe que ambos puntos de la línea tienen la misma coordenada x pero diferentes coordenadas y. Eso la convierte en una línea vertical, por lo que cualquier otro punto de la línea tendrá una coordenada x de -3.75. La respuesta correcta es (-3.75, -14.55).
Resumen
Pendiente describe la inclinación de una línea. La pendiente de cualquier línea permanece constante a lo largo de la línea. El talud también puede indicarle información sobre la dirección de la línea en el plano de coordenadas. La pendiente se puede calcular ya sea mirando la gráfica de una línea o usando las coordenadas de dos puntos cualesquiera en una línea. Hay dos fórmulas comunes para la pendiente: Slope = rise run y m=y2−y1x2−x1 dónde m= slope y (x1,y1) y (x2,y2) son dos puntos en la línea.
Las imágenes a continuación resumen las pendientes de diferentes tipos de líneas.