6.1: Conceptos geométricos básicos y figuras
- Page ID
- 112962
- Identificar y definir puntos, líneas, segmentos de línea, rayos y planos.
- Clasifica los ángulos como agudos, rectos, obtusos o rectos.
Introducción
Utilizas términos geométricos en el lenguaje cotidiano, muchas veces sin pensarlo. Por ejemplo, cada vez que dices “caminar por esta línea” o “cuidado, este camino rápidamente se orienta hacia la izquierda” estás usando términos geométricos para darle sentido al entorno que te rodea. Utiliza estos términos de manera flexible, y la gente generalmente sabe de lo que estás hablando.
En el mundo de las matemáticas, cada uno de estos términos geométricos tiene una definición específica. Es importante conocer estas definiciones —así como cómo se construyen diferentes figuras— para familiarizarse con el lenguaje de la geometría. Empecemos con una figura geométrica básica: el plano.
Figuras en un plano
Un plano es una superficie plana que continúa para siempre (o, en términos matemáticos, infinitamente) en todas las direcciones. Tiene dos dimensiones: largo y ancho.
Se puede visualizar un plano colocando un trozo de papel sobre una mesa. Ahora imagina que la hoja de papel permanece perfectamente plana y se extiende hasta donde puedes ver en dos direcciones, de izquierda a derecha y de adelante hacia atrás. Este gigantesco trozo de papel te da una idea de cómo es un plano geométrico: continúa infinitamente en dos direcciones. (Sin embargo, a diferencia del ejemplo de la hoja de papel, un plano geométrico no tiene altura.)
Un plano puede contener una serie de figuras geométricas. La idea geométrica más básica es un punto, que no tiene dimensiones. Un punto es simplemente una ubicación en el avión. Está representado por un punto. Tres puntos que no se encuentran en línea recta determinarán un plano.
La siguiente imagen muestra cuatro puntos, etiquetados A, B, C y D.
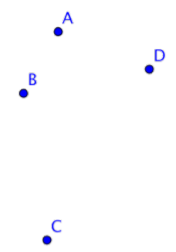
Dos puntos en un plano determinan una línea. Una línea es una figura unidimensional que se compone de un número infinito de puntos individuales colocados uno al lado del otro. En geometría, se supone que todas las líneas son rectas; si se doblan se llaman curva. Una línea continúa infinitamente en dos direcciones.
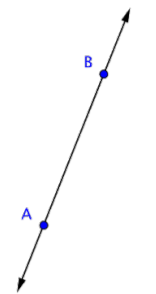
Abajo está la línea AB o, en notación geométrica,\(\overleftrightarrow{AB}\). Las flechas indican que la línea sigue yendo para siempre en las dos direcciones. Esta línea también podría llamarse línea BA. Si bien el orden de los puntos no importa para una línea, se acostumbra nombrar los dos puntos en orden alfabético.
La imagen de abajo muestra los puntos A y B y la línea\(\overleftrightarrow{AB}\).
Nombra la línea que se muestra en rojo.
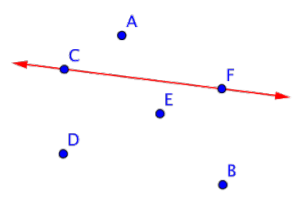
Solución
La línea roja pasa por los puntos C y F, por lo que la línea es\(\overleftrightarrow{CF}\).
Respuesta:\(\overleftrightarrow{CF}\)
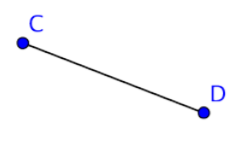
Hay dos cifras más a considerar. La sección entre dos puntos cualesquiera de una línea se denomina segmento de línea. Un segmento de línea puede ser muy largo, muy corto o en algún punto intermedio. La diferencia entre una línea y un segmento de línea es que el segmento de línea tiene dos puntos finales y una línea continúa para siempre. Un segmento de línea se denota por sus dos puntos finales, como en\(\overline{CD}\).
Un rayo tiene un punto final y continúa para siempre en una dirección. Los matemáticos nombran un rayo con notación como\(\overrightarrow{EF}\), donde el punto E es el punto final y F es un punto en el rayo. Al nombrar un rayo, siempre decimos primero el punto final. Obsérvese que\(\overrightarrow{FE}\) tendría el punto final en F, y continuaría a través de E, que es un rayo diferente al\(\overrightarrow{EF}\), que tendría un punto final en E, y continuaría a través de F.
El término “ray” puede ser familiar porque es una palabra común en inglés. A menudo se usa “Ray” cuando se habla de luz. Si bien un rayo de luz se asemeja al término geométrico “rayo”, no continúa para siempre, y tiene algo de ancho. Un rayo geométrico no tiene ancho; solo largo.
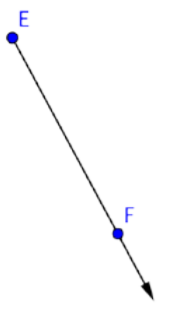
A continuación se muestra una imagen de ray EF o\(\overrightarrow{EF}\). Observe que el punto final es E.
Identifique cada línea y segmento de línea en la imagen de abajo.
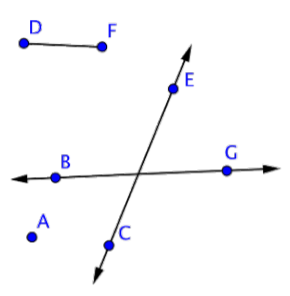
Solución
Dos puntos definen una línea, y una línea se denota con flechas. Hay dos líneas en esta imagen:\(\overleftrightarrow{CE}\) y\(\overleftrightarrow{BG}\).
Un segmento de línea es una sección entre dos puntos. \(\overline{DF}\)es un segmento de línea. Pero también hay dos segmentos de línea más en las propias líneas:\(\overline{CE}\) y\(\overline{BG}\).
Respuesta: Líneas:\(\overline{CE}\),\(\overline{BG}\)
Segmentos de línea:\(\overline{DF}\),\(\overline{CE}\),\(\overline{BG}\).
Identifica cada punto y rayo en la imagen de abajo.
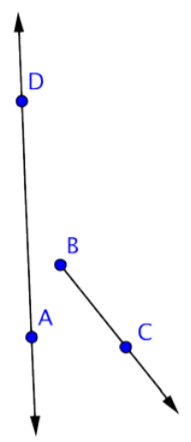
Solución
Hay cuatro puntos: A, B, C y D. También hay tres rayos, aunque sólo uno puede ser obvio.
\(\overrightarrow{BC}\)El rayo comienza en el punto B y pasa por C. Dos rayos más existen en línea\(\overleftrightarrow{AD}\): son\(\overrightarrow{DA}\) y\(\overrightarrow{AD}\).
Respuesta: Puntos: A, B, C, D
Rayos:\(\overrightarrow{BC}\),\(\overrightarrow{AD}\),\(\overrightarrow{DA}\)
¿Cuál de los siguientes no está representado en la imagen de abajo?
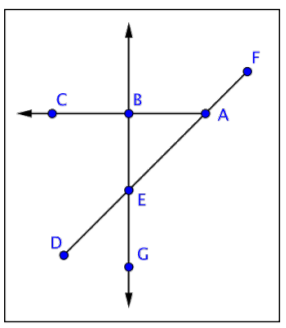
A) BG
B) BA
C)\(\overline{DF}\)
D) AC
Ángulos
Las líneas, los segmentos de línea, los puntos y los rayos son los bloques de construcción de otras figuras. Por ejemplo, dos rayos con un punto final común conforman un ángulo. El punto final común del ángulo se llama vértice.
A continuación se muestra el ángulo ABC. Este ángulo también se puede llamar ABC, CBA o simplemente B. Cuando esté nombrando ángulos, tenga cuidado de incluir el vértice (aquí, punto B) como la letra media.
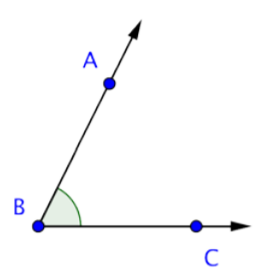
La imagen de abajo muestra algunos ángulos en un plano. Observe que la etiqueta de cada ángulo está escrita “punto-vértice-punto”, y la notación geométrica está en la forma ABC.
A veces los ángulos son muy estrechos; a veces son muy anchos. Cuando la gente habla del “tamaño” de un ángulo, se refiere al arco entre los dos rayos. La longitud de los rayos no tiene nada que ver con el tamaño del propio ángulo. Los dibujos de ángulos a menudo incluirán un arco (como se muestra arriba) para ayudar al lector a identificar el 'lado' correcto del ángulo.
Piensa en una cara de reloj analógico. Las manecillas de los minutos y las horas están ambas fijas en un punto en la mitad del reloj. A medida que pasa el tiempo, las manecillas giran alrededor del punto fijo, haciendo ángulos cada vez más grandes a medida que avanzan. La longitud de las manecillas no impacta en el ángulo que hacen las manos.
Un ángulo se mide en grados, representado por el símbolo º. Un círculo se define como tener 360º. (En skateboarding y básquetbol, “hacer un 360” se refiere a saltar y hacer una rotación completa del cuerpo.
Un ángulo recto es cualquier grado que mida exactamente 90º. Esto representa exactamente una cuarta parte del recorrido alrededor de un círculo. Los rectángulos contienen exactamente cuatro ángulos rectos. A menudo se usa una marca de esquina para denotar un ángulo recto, como se muestra en el DCB de ángulo recto a continuación.
Los ángulos que están entre 0º y 90º (menores que los ángulos rectos) se denominan ángulos agudos. Los ángulos que están entre 90º y 180º (mayores que los ángulos rectos y menores de 180º) se denominan ángulos obtusos. Y un ángulo que mide exactamente 180º se llama ángulo recto porque forma una línea recta.
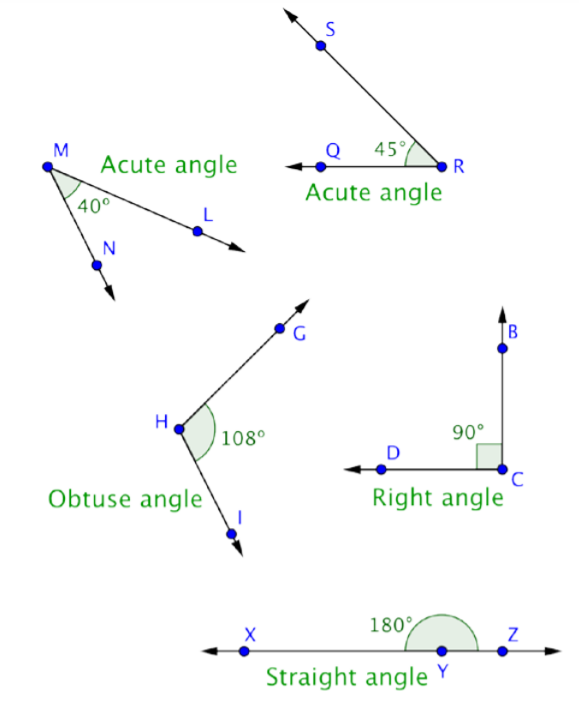
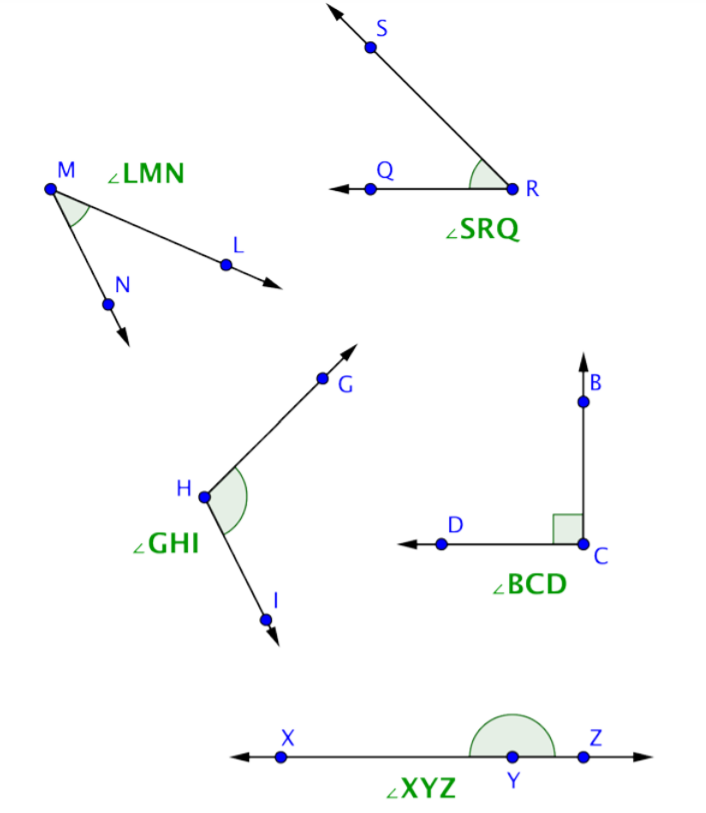
Etiquete cada ángulo de abajo como agudo, derecho u obtuso.
Solución
Puedes comenzar identificando cualquier ángulo recto.
GFI es un ángulo recto, como lo indica la marca de esquina en el vértice F.
Los ángulos agudos serán menores que GFI (o menores de 90º). Esto significa que DAB y MLN son agudos.
TQS es mayor que GFI, por lo que es un ángulo obtuso.
Respuesta: DAB y MLN son ángulos agudos. GFI es un ángulo recto. TQS es un ángulo obtuso.
Identifica cada punto, rayo y ángulo en la imagen de abajo.
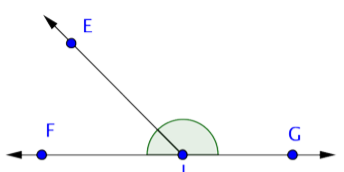
Solución
Comience por identificar cada punto de la figura. Hay 4: E, F, G y J.
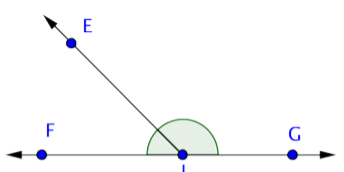
Ahora encuentra rayos. Un rayo comienza en un punto, y luego continúa por otro punto hacia el infinito (indicado por una flecha). Tres rayos comienzan en el punto J:\(\overrightarrow{JE}\),\(\overrightarrow{JF}\), y\(\overrightarrow{JG}\). Pero también fíjense que un rayo podría comenzar en el punto F y pasar por J y G, y otro podría comenzar en el punto G y pasar por J y F. Estos rayos pueden ser representados por\(\overrightarrow{GF}\) y\(\overrightarrow{FG}\).
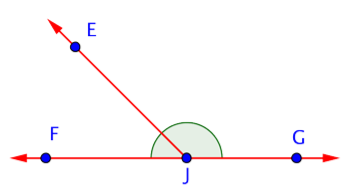
Por último, busca ángulos. EJG es obtuso, EJF es agudo y FJG es recto. (¡No olvides esos ángulos rectos!)
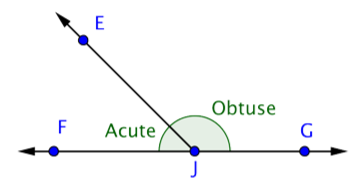
Respuesta: Puntos: E, F, G, J
Rayos:\(\overrightarrow{JE}\),\(\overrightarrow{JG}\),\(\overrightarrow{JF}\),\(\overrightarrow{GF}\),\(\overrightarrow{FG}\)
Ángulos: EJG, EJF, FJG
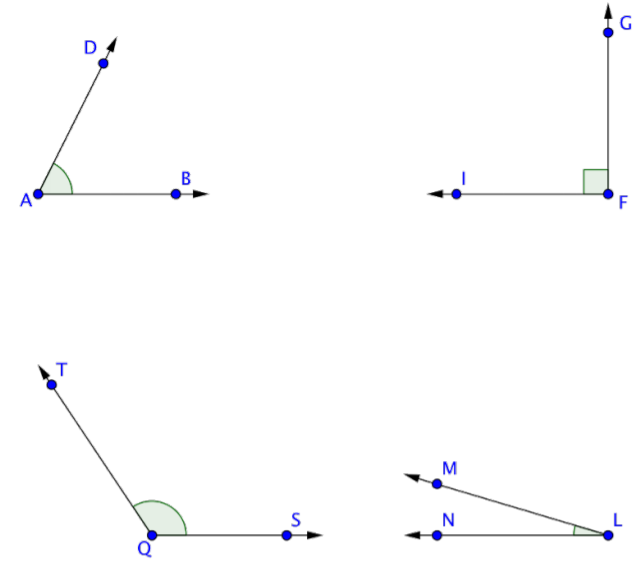
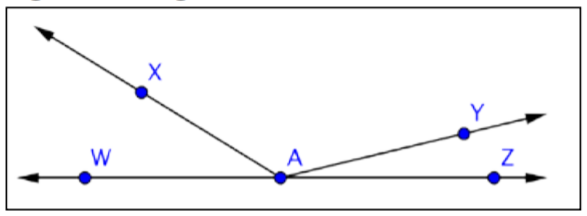
Identificar los ángulos agudos en la imagen dada:
Medición de ángulos con un Protractor
Aprender a medir ángulos puede ayudarle a sentirse más cómodo identificando la diferencia entre las mediciones de ángulo. Por ejemplo, ¿en qué se diferencia un ángulo de 135º de un ángulo de 45º?
La medición de ángulos requiere un transportador, que es una herramienta semicircular que contiene 180 marcas de hash individuales. Cada marca hash representa 1º. (Piénsalo así: un círculo es 360º, por lo que un semicírculo es 180º.) Para utilizar el transtractor, realice los siguientes tres pasos:
Paso 1. Alinee el vértice del ángulo con el punto en el medio del lado plano (parte inferior) del transportador,
Paso 2. Alinee un lado del ángulo con la línea en el transportador que está en la marca de cero grados, y
Paso 3. Mire la sección curva del prolongador para leer la medición.
El siguiente ejemplo te muestra cómo usar un prolongador para medir el tamaño de un ángulo.
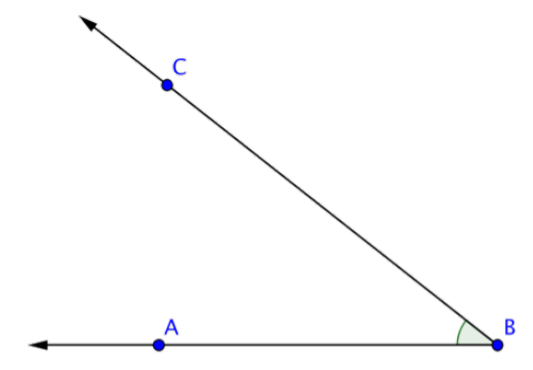
Use un traslador para medir el ángulo que se muestra a continuación.
Solución
Usa un transportadores para medir el ángulo.
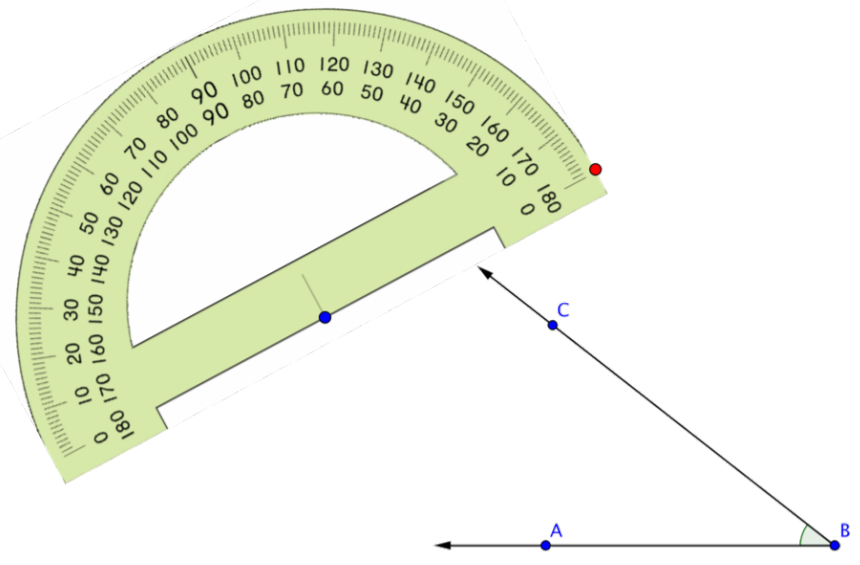
Alinee el punto azul en el traslador con el vértice del ángulo que desea medir.
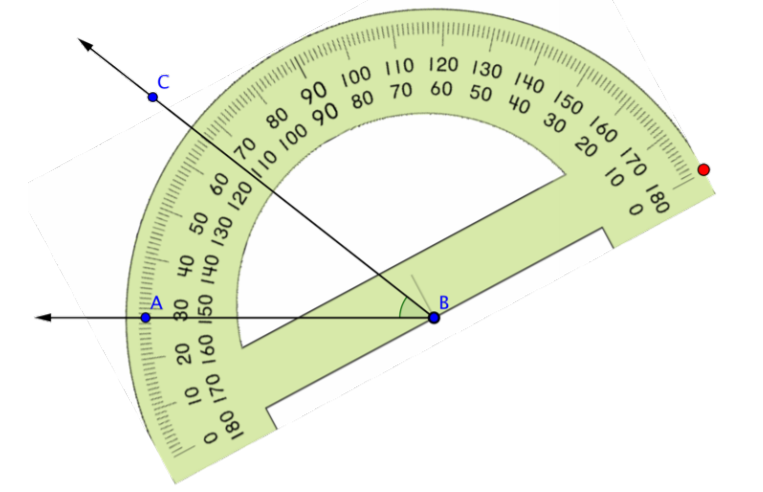
Gire el prolongador alrededor del vértice del ángulo hasta que el lado del ángulo esté alineado con la marca de 0 grados del prolongador.
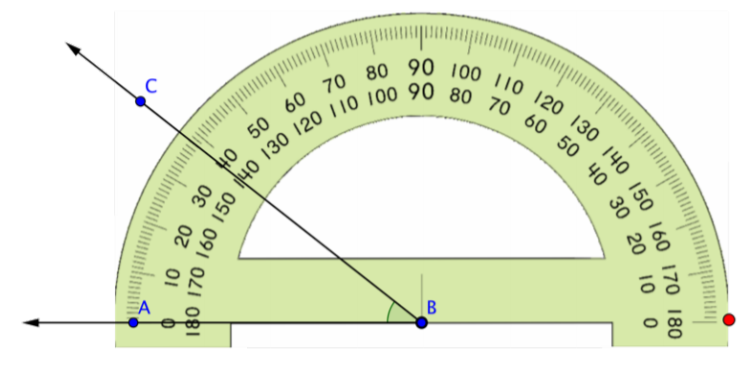
Lee la medición, en grados, del ángulo. Comience con el lado del ángulo que esté alineado con la marca 0º del transportador y cuente hacia arriba desde 0º. Este ángulo mide 38º.
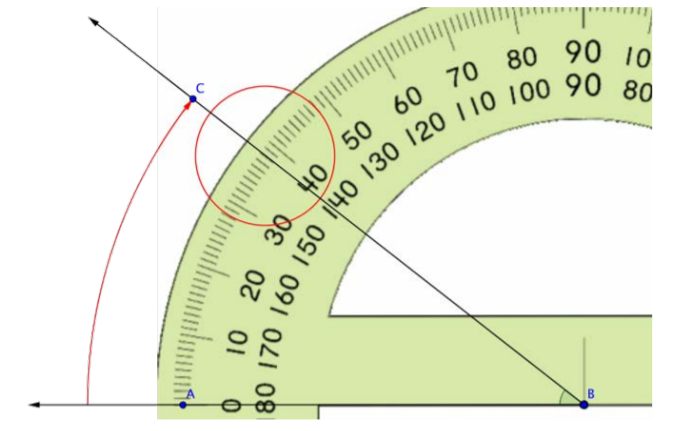
Respuesta: El ángulo mide 38º.
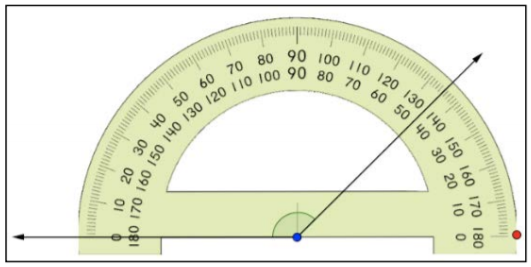
¿Cuál es la medida del ángulo que se muestra a continuación?
Resumen
La geometría comienza con conceptos simples como puntos, líneas, segmentos, rayos, etc. y se expande con ángulos. Como podemos ver en esta sección, existen múltiples tipos de ángulos y varias formas de medirlos. La forma más precisa de medir un ángulo es usar un prolongador. Cuando juntamos ángulos, obtenemos formas geométricas y sólidos, que discutimos en futuras secciones. A continuación, discutimos las líneas y el uso de propiedades para obtener medidas de ángulos.
- BA; esta imagen no muestra ningún rayo que comience en el punto B y pase por el punto A.
- WAX y YAZ x; ambos WAX y YAZ son ángulos agudos.
- 135º; este traslador está alineado correctamente, y la medición correcta es 135º.
6.1.1: Propiedades de los ángulos
- Identificar líneas paralelas y perpendiculares.
- Encuentra medidas de ángulos.
- Identificar ángulos complementarios y suplementarios.
Introducción
Imagina dos líneas separadas y distintas en un plano. Hay dos posibilidades para estas líneas: o se cruzarán en un punto, o nunca se cruzarán. Cuando dos líneas se cruzan, se forman cuatro ángulos. Entender cómo estos ángulos se relacionan entre sí puede ayudarte a averiguar cómo medirlos, incluso si solo tienes información sobre el tamaño de un ángulo.
Paralelo y perpendicular
Las líneas paralelas son dos o más líneas que nunca se cruzan. Asimismo, los segmentos de línea paralelos son dos segmentos de línea que nunca se cruzan aunque los segmentos de línea se convirtieran en líneas que continuaron para siempre. Ejemplos de segmentos de líneas paralelas están a tu alrededor, en los dos lados de esta página y en los estantes de una estantería. Cuando ves líneas o estructuras que parecen correr en la misma dirección, nunca se cruzan entre sí, y siempre están a la misma distancia, hay muchas posibilidades de que sean paralelas.
Las líneas perpendiculares son dos líneas que se cruzan en un ángulo de 90º (recto). Y los segmentos de línea perpendiculares también se cruzan en un ángulo de 90º (recto). También se pueden ver ejemplos de líneas perpendiculares en todas partes, en papel cuadriculado, en el patrón de cruce de carreteras en una intersección, hasta las líneas de colores de una camisa a cuadros. En nuestra vida cotidiana, puede estar feliz de llamar a dos líneas perpendiculares si simplemente parecen estar en ángulo recto entre sí. Sin embargo, al estudiar geometría, es necesario asegurarse de que dos líneas se crucen en un ángulo de 90º antes de declararlas perpendiculares.
La imagen de abajo muestra algunas líneas paralelas y perpendiculares. El símbolo geométrico para paralelo es ||, por lo que puedes mostrar ese AB || CD. Las líneas paralelas también se indican a menudo con la marca >> en cada línea (o solo una > en cada línea). Las líneas perpendiculares se indican con el símbolo, para que puedas escribir\(\overleftrightarrow{WX} ⊥ \overleftrightarrow{YZ}\).
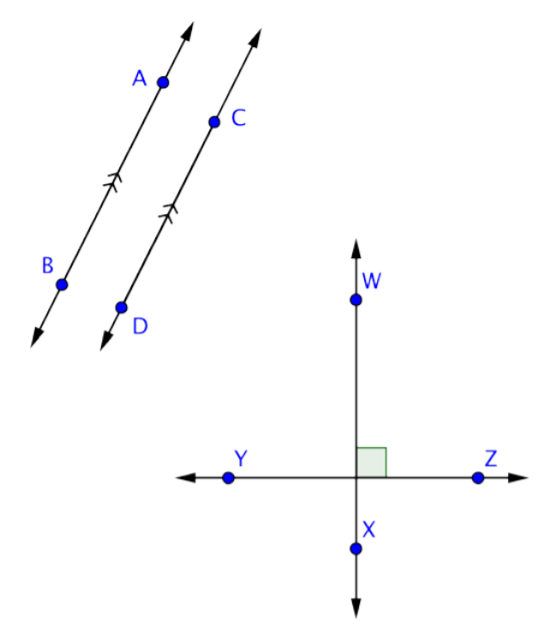
Si dos líneas son paralelas, entonces cualquier línea que sea perpendicular a una línea también será perpendicular a la otra línea. Del mismo modo, si dos líneas son ambas perpendiculares a la misma línea, entonces esas dos líneas son paralelas entre sí. Echemos un vistazo a un ejemplo e identifiquemos algunos de estos tipos de líneas.
Identifica un conjunto de líneas paralelas y un conjunto de líneas perpendiculares en la imagen de abajo.
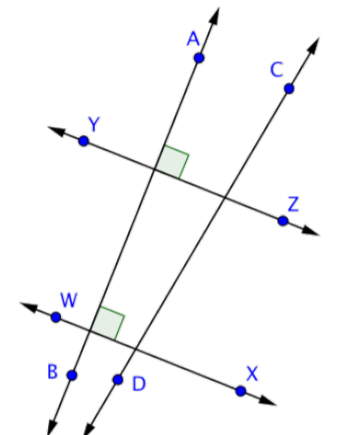
Solución
Las líneas paralelas nunca se encuentran, y las líneas perpendiculares se cruzan en ángulo recto. \(\overleftrightarrow{AB}\)y\(\overleftrightarrow{CD}\) no se crucen en esta imagen, pero si imaginas extender ambas líneas, pronto se cruzarán. Entonces, no son ni paralelos ni perpendiculares.
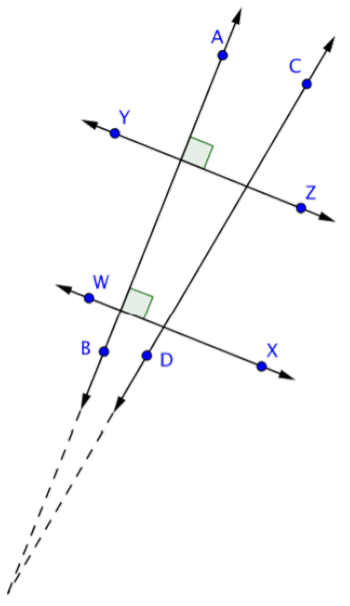
\(\overleftrightarrow{AB}\)es perpendicular a ambos\(\overleftrightarrow{WX}\) y\(\overleftrightarrow{YZ}\), como lo indican las marcas de ángulo recto en la intersección de esas líneas.
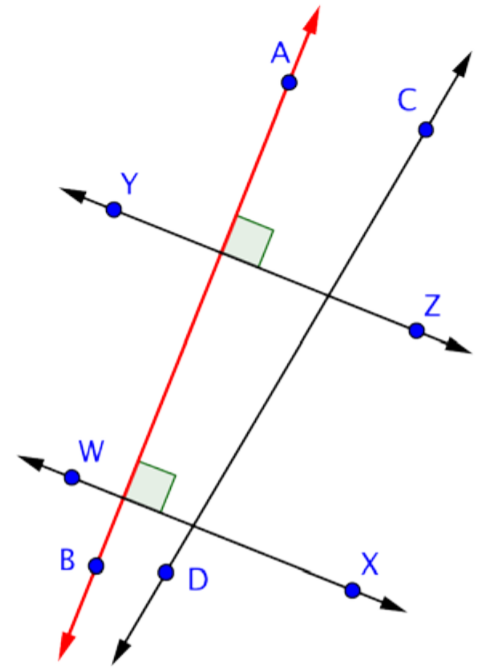
Ya que\(\overleftrightarrow{AB}\) es perpendicular a ambas líneas, entonces\(\overleftrightarrow{WX}\) y\(\overleftrightarrow{YZ}\) son paralelas.
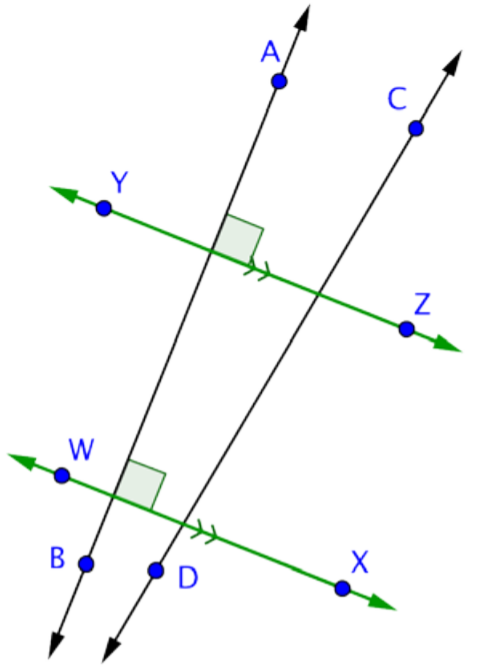
Respuesta:\(\overleftrightarrow{WX}\) ||\(\overleftrightarrow{YZ}\)
\(\overleftrightarrow{AB}\)\(\overleftrightarrow{WX}\)\(\overleftrightarrow{AB}\),\(\overleftrightarrow{YZ}\)
¿Qué declaración representa con mayor precisión la imagen de abajo?
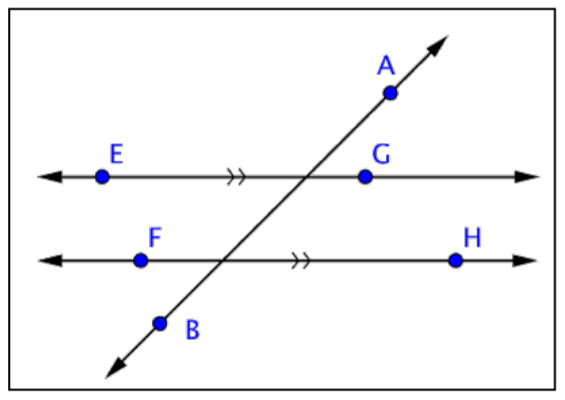
A) EF || GH
B) AB EG
C) FH || EG
D) AB || FH
Encontrar mediciones de ángulo
Entender cómo se relacionan las líneas paralelas y perpendiculares puede ayudarte a determinar las medidas de algunos ángulos desconocidos. Para comenzar, lo único que debes recordar es que las líneas perpendiculares se cruzan en un ángulo de 90º y que un ángulo recto mide 180º.
La medida de un ángulo como A se escribe como MA. Mira el siguiente ejemplo. ¿Cómo se pueden encontrar las medidas de los ángulos sin marcar?
Encuentra la medición de IJF.
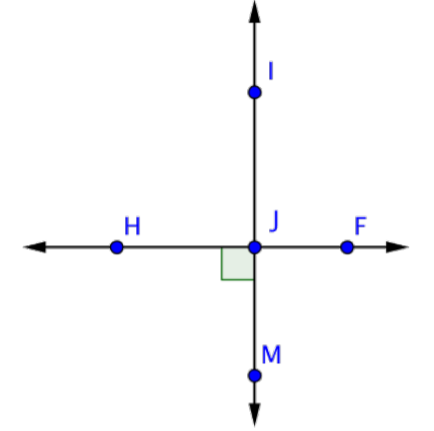
Solución
Solo un ángulo, HJM, está marcado en la imagen. Observe que es un ángulo recto, por lo que mide 90º. HJM está formado por la intersección de líneas\(\overleftrightarrow{IM}\) y\(\overleftrightarrow{HF}\). Ya que\(\overleftrightarrow{IM}\) es una línea, IJM es un ángulo recto que mide 180º.
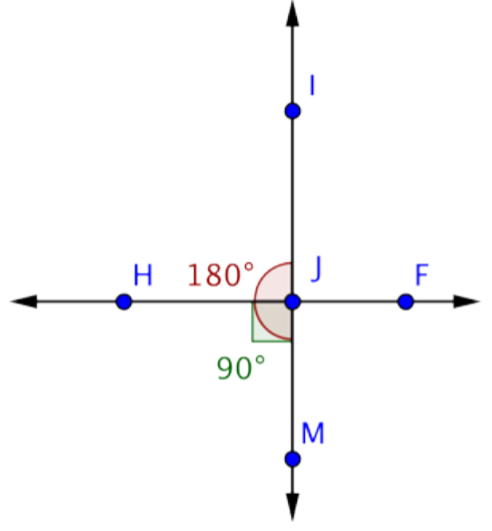
Puede utilizar esta información para encontrar la medición de HJI:
MhJM + MhJi = MiJM
90º + MHji = 180º
MHji = 90º
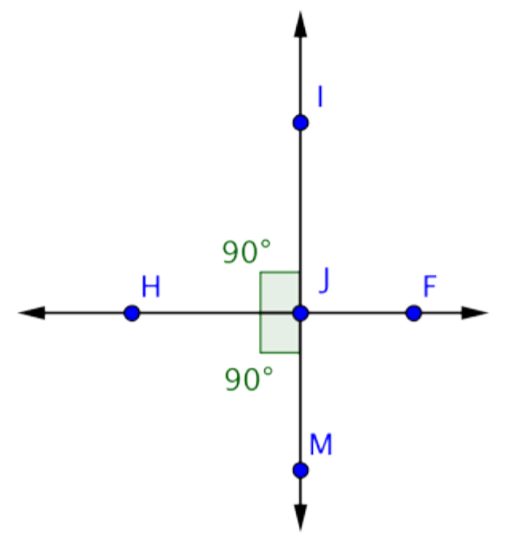
Ahora usa la misma lógica para encontrar la medición de IJF. IJF está formado por la intersección de líneas\(\overleftrightarrow{IM}\) y\(\overleftrightarrow{HF}\). Ya que\(\overleftrightarrow{HF}\) es una línea, HJF será un ángulo recto que mide 180º.
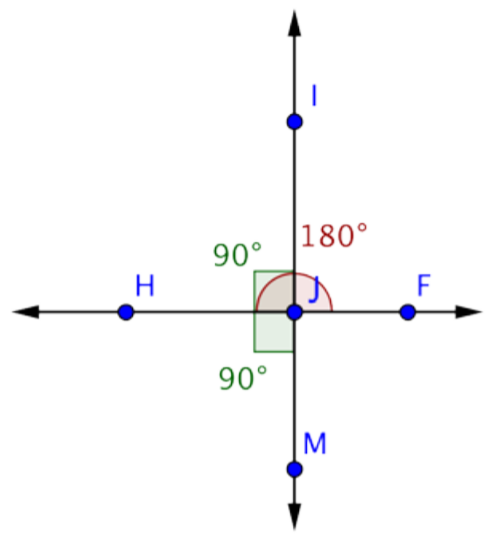
Sabes que HJI mide 90º. Usa esta información para encontrar la medida de IJF:
mhJM + MiJF = MhJF
90º + MIJF = 180º
MIJF = 90º
Respuesta: MIJF = 90º
En este ejemplo, es posible que hayas notado que los ángulos HJI, IJF y HJM son todos ángulos rectos. (Si te pidieran que encontraras la medición de FJM, también encontrarías que ese ángulo es de 90º). Esto es lo que sucede cuando dos líneas son perpendiculares: los cuatro ángulos creados por la intersección son todos ángulos rectos.
Sin embargo, no todas las intersecciones ocurren en ángulo recto. En el siguiente ejemplo, observe cómo puede usar la misma técnica que se muestra arriba (usando ángulos rectos) para encontrar la medición de un ángulo faltante.
Encuentra la medición de DAC.
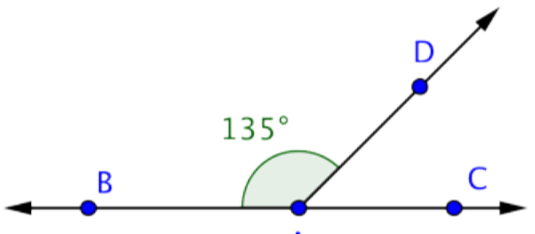
Solución
Esta imagen muestra la línea\(\overleftrightarrow{BC}\) y el rayo que se\(\overrightarrow{AD}\) cruzan en el punto A. La medición de BAD es 135º. Puede utilizar ángulos rectos para encontrar la medición de DAC.
BAC es un ángulo recto, por lo que mide 180º.
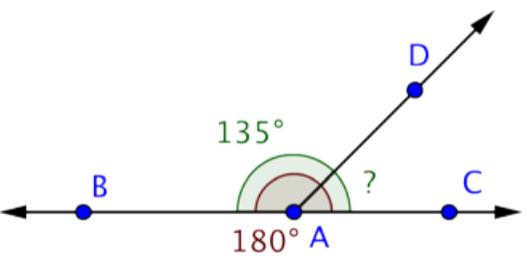
Utilice esta información para encontrar la medición de DAC.
MBad + Mdac = MBac
135º + MDAC = 180º
MDAC = 45º
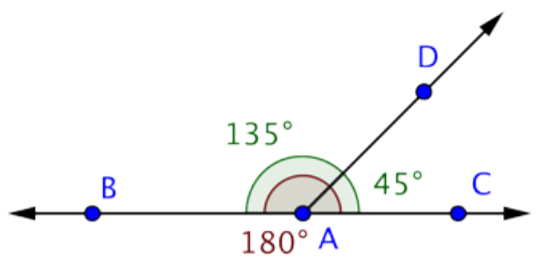
Respuesta: Mdac = 45º
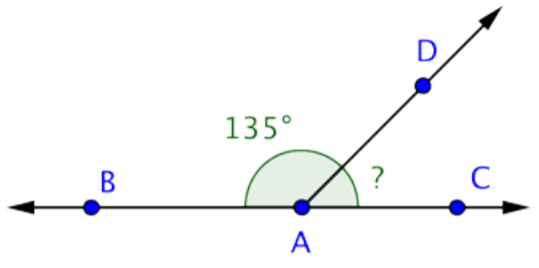
Encuentra la medición de CAD.
Complementario y Complement
En el ejemplo anterior, mbac y mdac suman 180º. Dos ángulos cuyas medidas suman 180º se denominan ángulos suplementarios. También hay un término para dos ángulos cuyas medidas suman 90º, se llaman ángulos complementarios.
Una forma de recordar la diferencia entre los dos términos es que “esquina” y “complementario” comienzan cada uno con c (un ángulo de 90º parece una esquina), mientras que recto y “suplementario” comienzan cada uno con s (un ángulo recto mide 180º).
Si puede identificar ángulos suplementarios o complementarios dentro de un problema, encontrar mediciones de ángulo faltantes suele ser simplemente una cuestión de sumar o restar.
Dos ángulos son suplementarios. Si uno de los ángulos mide 48º, ¿cuál es la medida del otro ángulo?
Solución
Dos ángulos suplementarios conforman un ángulo recto, por lo que las medidas de los dos ángulos serán de 180º.
Ma + Mb = 180º
Conoces la medición de un ángulo. Para encontrar la medición del segundo ángulo, restar 48º de 180º.
48º+ Mb = 180º
Mb = 180º - 48º
Mb = 132º
Respuesta: La medida del otro ángulo es de 132º
Encuentra la medición de AXZ.
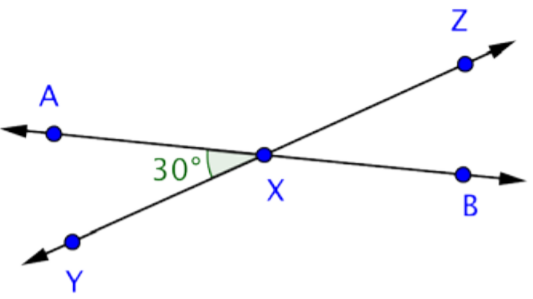
Solución
Esta imagen muestra dos líneas que se cruzan,\(\overleftrightarrow{AB}\) y\(\overleftrightarrow{YZ}\). Se cruzan en el punto X, formando cuatro ángulos. Los ángulos AXY y AXZ son suplementarios porque juntos forman el ángulo recto YXZ.
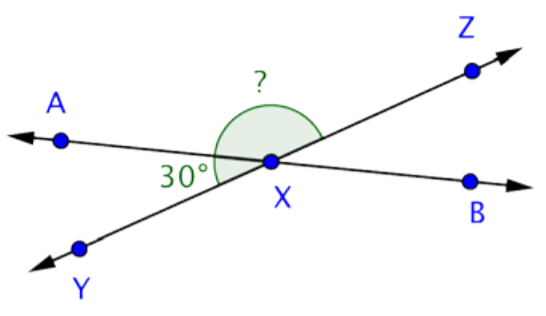
Usa esta información para encontrar la medición de AXZ.
Maxy + MaxZ = MyxZ
30º + MaxZ = 180º
maxZ = 150º
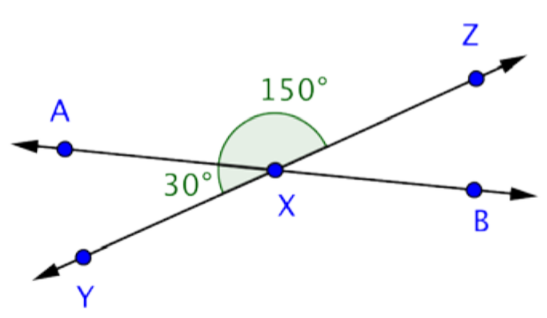
Respuesta: MaxZ = 150º
Encuentra la medición de BAC.
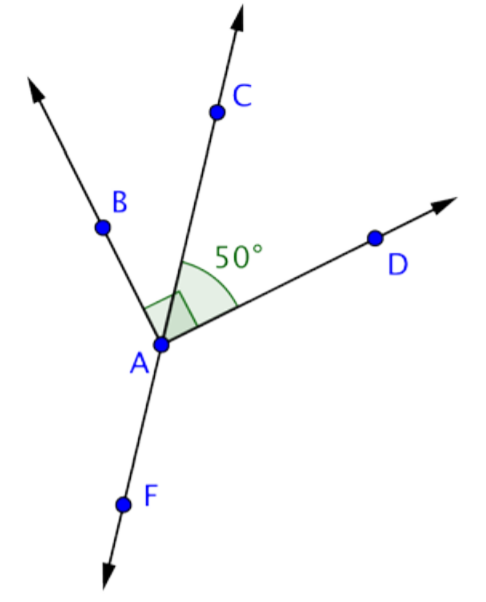
Solución
Esta imagen muestra la línea\(\overleftrightarrow{CF}\) y los rayos\(\overleftrightarrow{AB}\) y\(\overleftrightarrow{AD}\), todos intersectándose en el punto A. Ángulo BAD es un ángulo recto. Los ángulos BAC y CAD son complementarios porque juntos crean BAD.
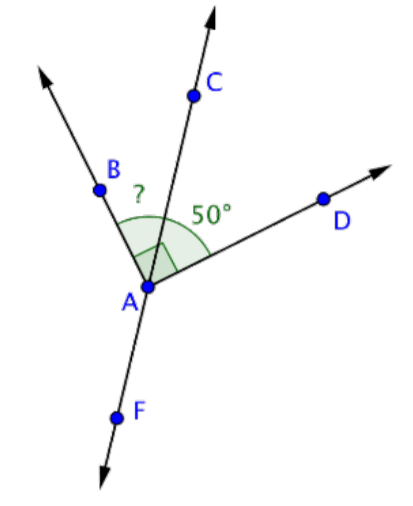
Usa esta información para encontrar la medición de BAC.
MBac + Mcad = MBad
MBac + 50º = 90º
MBac = 40º
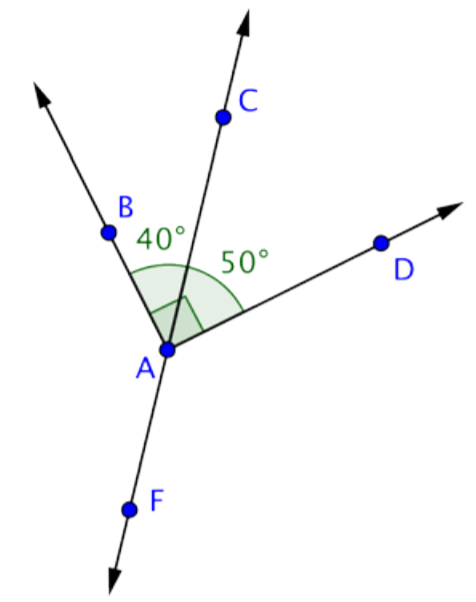
Respuesta: Mbac = 40º
Encuentra la medición de CAD.
Solución
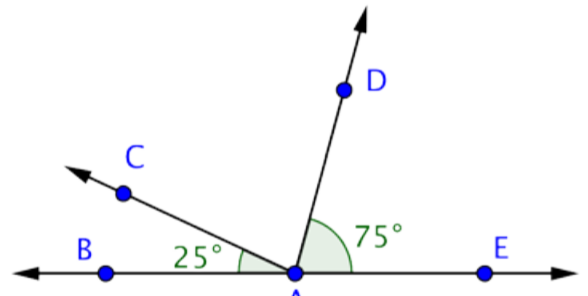
Conoce las medidas de dos ángulos aquí: CAB y DAE. También sabes que Mbae = 180º.
Utilice esta información para encontrar la medición de CAD.
mbac + mcad + mdae = mbaE
25º + Mcad + 75º = 180º
Mcad + 100º = 180º
MCAD = 80º
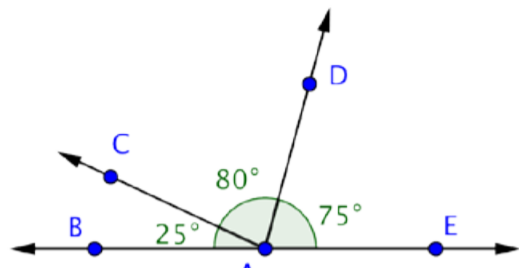
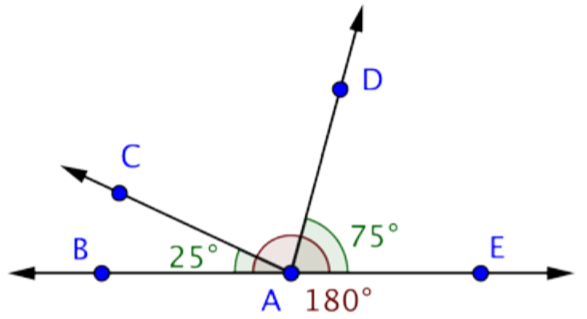
Respuesta: Mcad = 80º
¿Qué par de ángulos es complementario?
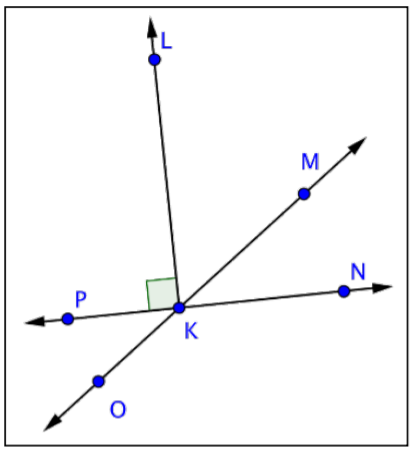
A) PKO y MKN
B) PKO y PKM
C) LKP y LKN
D) LKM y MKN
Resumen
Las líneas paralelas no se cruzan, mientras que las perpendiculares se cruzan en un ángulo de 90º. Se dice que dos ángulos cuyas medidas suman 180º son complementarios, y dos ángulos cuyas medidas suman 90º se dice que son complementarios. Para la mayoría de los pares de líneas que se cruzan, todo lo que necesita es la medición de un ángulo para encontrar las medidas de todos los demás ángulos formados por la intersección.
- C) FH || EG; tanto EG como FH están marcados con >> en cada línea, y esas marcas significan que son paralelas.
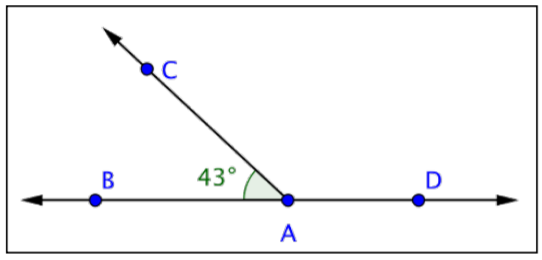
- 137º; BAD es un ángulo recto que mide 180º. Dado que BAC mide 43º, la medida de CAD debe ser 180º — 43º = 137º.
- D) LKM y MKN; las medidas de dos ángulos complementarios sumarán hasta 90º. LKP es un ángulo recto, por lo que LKN también debe ser un ángulo recto. LKM + MKN = LKN, por lo que LKM y MKN son complementarios.
6.1.2: Triángulos
- Identificar triángulos equiláteros, isósceles, escalenos, agudos, derechos y obtusos.
- Identificar si los triángulos son similares, congruentes, o ninguno.
- Identificar los lados correspondientes de triángulos congruentes y similares.
- Encuentra las medidas faltantes en un par de triángulos similares.
- Resolver problemas de aplicación que involucran triángulos similares
Introducción
Las formas geométricas, también llamadas figuras, son una parte importante del estudio de la geometría. El triángulo es una de las formas básicas en geometría. Es la forma más simple dentro de una clasificación de formas llamadas polígonos. Todos los triángulos tienen tres lados y tres ángulos, pero vienen en muchas formas y tamaños diferentes. Dentro del grupo de todos los triángulos, se utilizan las características de los lados y ángulos de un triángulo para clasificarlo aún más. Los triángulos tienen algunas características importantes, y comprender estas características permite aplicar las ideas en problemas del mundo real.
Clasificación y Nombramiento de Triángulos
Un polígono es una figura plana cerrada con tres o más lados rectos. Los polígonos tienen cada uno un nombre especial basado en el número de lados que tienen. Por ejemplo, al polígono con tres lados se le llama triángulo porque “tri” es un prefijo que significa “tres”. Su nombre también indica que este polígono tiene tres ángulos. El prefijo “poli” significa muchos.
La siguiente tabla muestra y describe tres clasificaciones de triángulos. Observe cómo se utilizan los tipos de ángulos en el triángulo para clasificar el triángulo.
| Nombre del Triángulo | Imagen de Triángulo | Descripción |
| Triángulo Agudo | 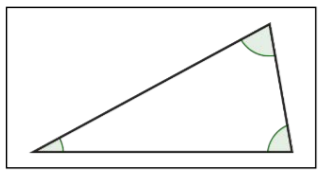 |
Un triángulo con 3 ángulos agudos (3 ángulos que miden entre 0° y 90°). |
| Triángulo Obtuso | 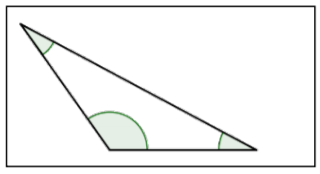 |
Un triángulo con 1 ángulo obtuso (1 ángulo que mide entre 90° y 180°). |
| Triángulo Recto | 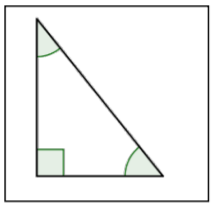 |
Un triángulo que contiene un ángulo recto (1 ángulo que mide 90°). Tenga en cuenta que el ángulo recto se muestra con una marca de esquina y no necesita etiquetarse 90°. |
La suma de las medidas de los tres ángulos interiores de un triángulo es siempre 180°. Este hecho se puede aplicar para encontrar la medida del tercer ángulo de un triángulo, si se le dan los otros dos. Considera los ejemplos a continuación.
Un triángulo tiene dos ángulos que miden 35° y 75°. Encuentra la medida del tercer ángulo.
Solución
La suma de los tres ángulos interiores de un triángulo es de 180°.
35° + 75° +\(x\) = 180°
Encuentra el valor de\(x\).
110º +\(x\) = 180º
\(x\)= 180° ‒ 110º
\(x\)= 70°
Respuesta: El tercer ángulo del triángulo mide 70°.
Uno de los ángulos en un triángulo rectángulo mide 57º. Encuentra la medida del tercer ángulo.
Solución
La suma de los tres ángulos de un triángulo es de 180°. Uno de los ángulos tiene una medida de 90° ya que es un triángulo rectángulo.
57° + 90° +\(x\) = 180°
Simplificar.
147º +\(x\) = 180°
Encuentra el valor de\(x\).
\(x\)= 180º - 147º
\(x\)= 33º
Respuesta: El tercer ángulo del triángulo rectángulo mide 33°.
Existe una convención establecida para nombrar triángulos. Las etiquetas de los vértices del triángulo, que generalmente son letras mayúsculas, se utilizan para nombrar a un triángulo.
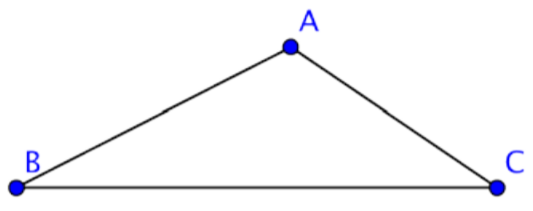
Se puede llamar a este triángulo ABC o ∆ABC ya que A, B y C son vértices del triángulo. Al nombrar el triángulo, puede comenzar con cualquier vértice. Entonces mantén las letras en orden a medida que recorres el polígono. El triángulo anterior podría ser nombrado de varias maneras: ∆ABC, o ∆CBA. Los lados del triángulo son segmentos de línea AB, AC y CB.
Así como los triángulos pueden clasificarse como agudos, obtusos o rectos en función de sus ángulos, también pueden clasificarse por la longitud de sus lados. Los lados de igual longitud se denominan lados congruentes. Si bien designamos un segmento que une los puntos A y B por la notación\(\overline{AB}\), designamos la longitud de un segmento que une los puntos A y B por la notación AB sin una barra de segmento sobre él. La longitud AB es un número, y el segmento\(\overline{AB}\) es la colección de puntos que conforman el segmento.
Los matemáticos muestran congruencia al poner un símbolo de marca hash a través de la mitad de lados de igual longitud. Si la marca hash es la misma en uno o más lados, entonces esos lados son congruentes. Si los lados tienen diferentes marcas de hash, no son congruentes. En la siguiente tabla se muestra la clasificación de los triángulos por sus longitudes laterales.
| Nombre del Triángulo | Imagen de Triángulo | Descripción |
| Triángulo Equilátero | 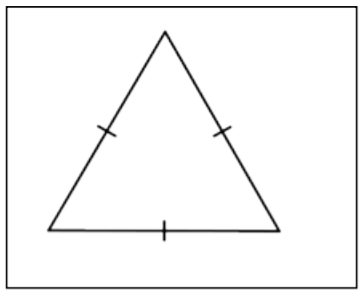 |
Un triángulo cuyos tres lados tienen la misma longitud. Estos lados de igual longitud se denominan lados congruentes. |
| Triángulo Isósceles | 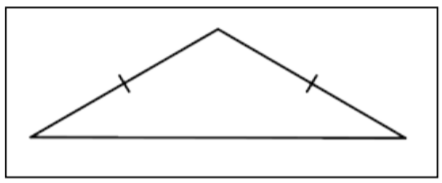 |
Un triángulo con exactamente dos lados congruentes. |
| Triángulo Escaleno |  |
Un triángulo en el que los tres lados tienen una longitud diferente. |
Para describir un triángulo aún más específicamente, se puede utilizar información tanto sobre sus lados como sobre sus ángulos. Considera este ejemplo.
Clasifica el triángulo a continuación.
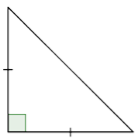
Solución
Observe qué tipo de ángulos tiene el triángulo. Dado que un ángulo es un ángulo recto, este es un triángulo recto.
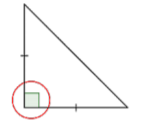
Observe las longitudes de los lados. ¿Hay marcas de congruencia u otras etiquetas?
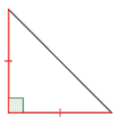
Las marcas de congruencia nos dicen que hay dos lados de igual longitud. Entonces, este es un triángulo isósceles.
Respuesta: Este es un triángulo rectángulo isósceles
Clasificar el triángulo dado.
Identificación de triángulos congruentes y similares
Dos triángulos son congruentes si son exactamente del mismo tamaño y forma. En triángulos congruentes, las medidas de los ángulos correspondientes y las longitudes de los lados correspondientes son iguales. Considera los dos triángulos que se muestran a continuación:
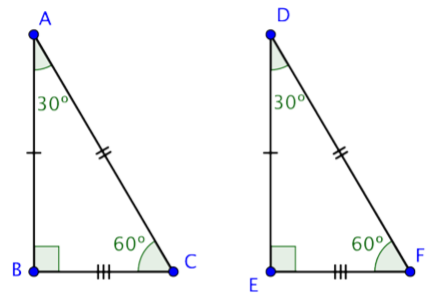
Dado que tanto B como E son ángulos rectos, estos triángulos son triángulos rectos. Llamemos a estos dos triángulos ∆ABC y ∆DEF. Estos triángulos son congruentes si cada par de lados correspondientes tiene longitudes iguales y cada par de ángulos correspondientes tiene la misma medida.
Los lados correspondientes son opuestos a los ángulos correspondientes.
↔ significa “corresponde a”
B ↔ E
A ↔ D
C ↔ F
\(\overline{AB}\)↔\(\overline{DE}\)
\(\overline{AC}\)↔\(\overline{DF}\)
\(\overline{BC}\)↔\(\overline{EF}\)
∆ABC y ∆DEF son triángulos congruentes ya que los lados correspondientes y los ángulos correspondientes son iguales.
Echemos un vistazo a otro par de triángulos. A continuación se presentan los triángulos ∆ABC y ∆RST.
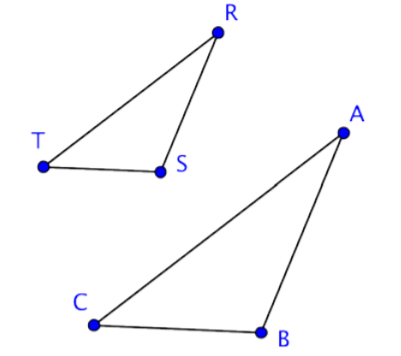
Estos dos triángulos seguramente no son congruentes porque ∆RST es claramente más pequeño en tamaño que ∆ABC. Pero, a pesar de que no son del mismo tamaño, sí se parecen entre sí. Tienen la misma forma. Los ángulos correspondientes de estos triángulos parecen tener la misma medida exacta, y si lo hicieran serían ángulos congruentes y llamaríamos a los triángulos triángulos similares.
Los ángulos congruentes están marcados con marcas hash, así como los lados congruentes lo están.
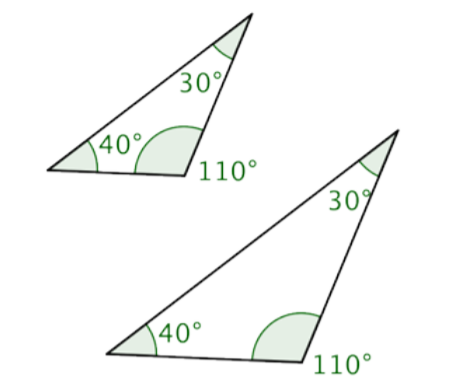
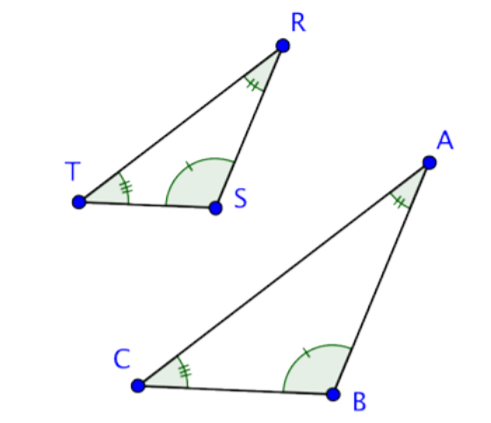
También podemos mostrar ángulos congruentes usando múltiples bandas dentro del ángulo, en lugar de múltiples marcas hash en una banda. A continuación se muestra una imagen usando múltiples bandas dentro del ángulo.
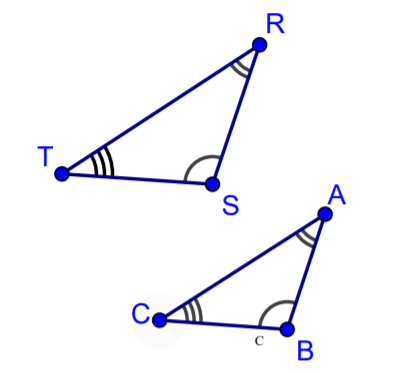
Si los ángulos correspondientes de dos triángulos tienen las mismas medidas se denominan triángulos similares. Este nombre tiene sentido porque tienen la misma forma, pero no necesariamente el mismo tamaño. Cuando un par de triángulos es similar, los lados correspondientes son proporcionales entre sí. Eso significa que existe un factor de escala consistente que se puede utilizar para comparar los lados correspondientes. En el ejemplo anterior, las longitudes laterales del triángulo más grande son 1.4 veces la longitud del triángulo más pequeño. Entonces, triángulos similares son proporcionales entre sí.
El hecho de que dos triángulos se vean similares no significa que sean triángulos similares en el sentido matemático de la palabra. Comprobando que los ángulos correspondientes tengan igual medida es una forma de asegurarse que los triángulos son similares.
Lados correspondientes de triángulos similares
Existe otro método para determinar la similitud de triángulos que implica comparar las proporciones de las longitudes de los lados correspondientes.
Si las relaciones de los pares de lados correspondientes son iguales, los triángulos son similares.
Considera los dos triángulos a continuación.
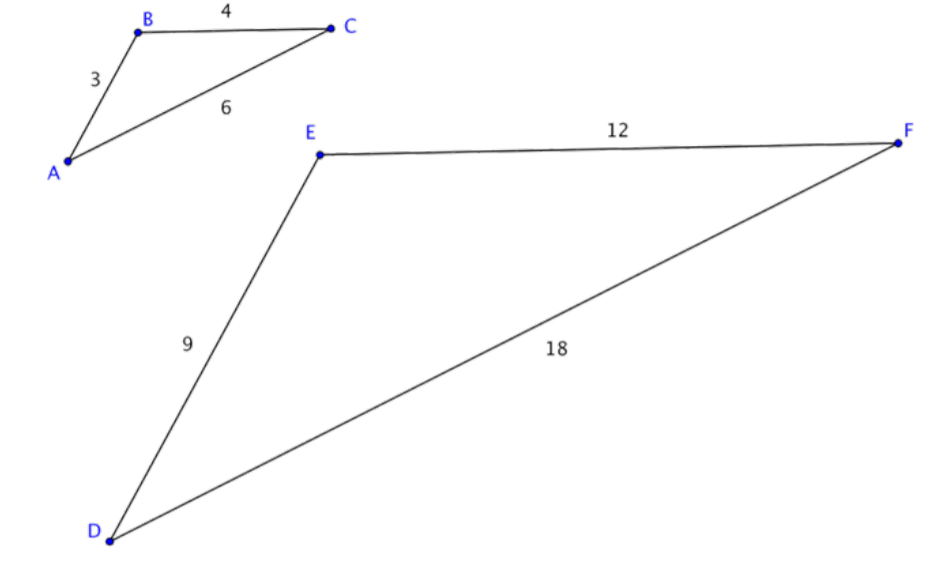
∆ABC no es congruente con ∆DEF porque las longitudes laterales de ∆DEF son más largas que las de ∆ABC. Entonces, ¿estos triángulos son similares? Si lo son, los lados correspondientes deben ser proporcionales.
Dado que estos triángulos están orientados de la misma manera, puedes emparejar los lados izquierdo, derecho e inferior:\(\overline{AB}\) y\(\overline{DE}\),\(\overline{BC}\) y\(\overline{EF}\),\(\overline{AC}\) y\(\overline{DF}\). (Podría llamarlos los dos lados más cortos, los dos lados más largos y los dos lados sobrantes y llegar a las mismas proporciones). Ahora veremos las proporciones de sus longitudes.
\( \dfrac{\overline{AB}}{\overline{DE}} = \dfrac{\overline{BC}}{\overline{EF}} = \dfrac{\overline{AC}}{\overline{DF}} \)
Sustituyendo los valores de longitud lateral en la proporción, se ve que es cierto:
\( \dfrac{3}{9} = \dfrac{4}{12} = \dfrac{6}{18} \)
Si los lados correspondientes son proporcionales, entonces los triángulos son similares. Los triángulos ABC y DEF son similares, pero no congruentes.
Usemos esta idea de lados proporcionales correspondientes para determinar si dos triángulos más son similares.
Determina si los triángulos de abajo son similares viendo si sus lados correspondientes son proporcionales.
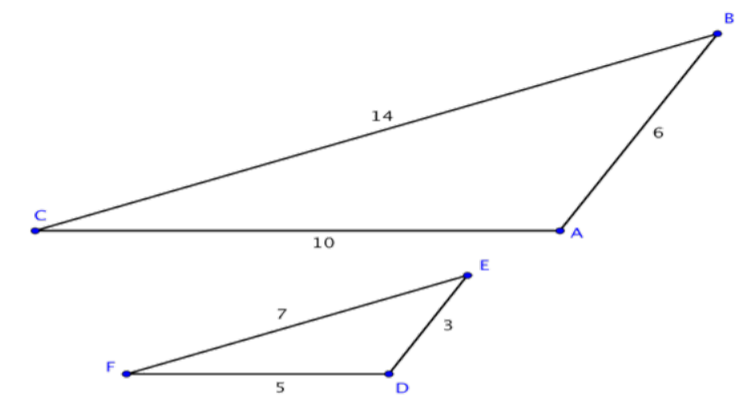
Solución
Primero determinar los lados correspondientes, los cuales son ángulos correspondientes opuestos.
\(\overline{CA}\)↔\(\overline{FD}\)
\(\overline{AB}\)↔\(\overline{DE}\)
\(\overline{BC}\)↔\(\overline{EF}\)
Escribe las longitudes de lado correspondientes como proporciones.
\( \dfrac{\overline{CA}}{\overline{FD}} = \dfrac{\overline{AB}}{\overline{DE}} = \dfrac{\overline{BC}}{\overline{EF}} \)
Sustituya las longitudes de los lados en las relaciones y determine si las proporciones de los lados correspondientes son equivalentes. Lo son, por lo que los triángulos son similares.
\( \dfrac{10}{5} = \dfrac{6}{3} = \dfrac{14}{7} \)
\(2 = 2 = 2\)
Respuesta: ∆ABC y ∆DEF son similares.
El símbolo matemático ~ significa “es similar a”. Entonces, puedes escribir ∆ABC es similar a ∆DEF como ∆ABC ~ ∆DEF.
Determinar si los dos triángulos son similares, congruentes o ninguno.
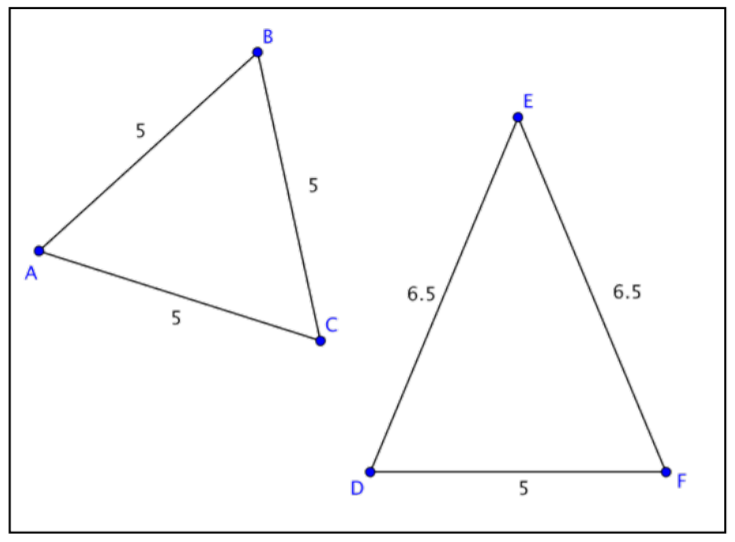
Encontrar mediciones faltantes en triángulos similares
Puedes encontrar las medidas faltantes en un triángulo si conoces algunas medidas de un triángulo similar. Veamos un ejemplo.
∆ABC y ∆XYZ son triángulos similares. ¿Cuál es la longitud del lado BC?
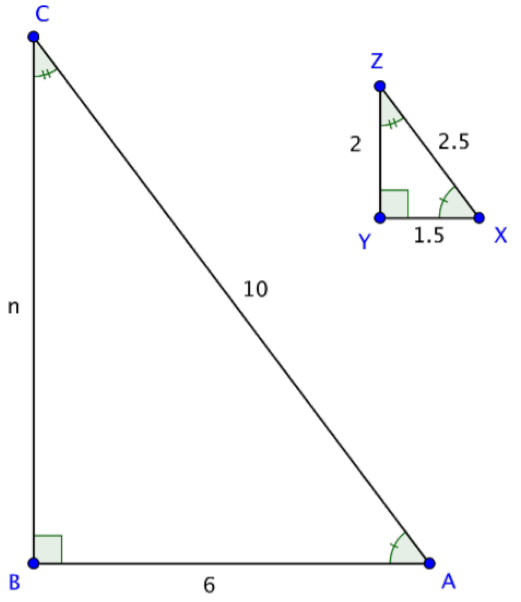
Solución
En triángulos similares, las proporciones de los lados correspondientes son proporcionales. Establecer una proporción de dos proporciones, una que incluya el lado faltante.
\(\dfrac{BC}{YZ} = \dfrac{AB}{XY}\)
Sustituir en las longitudes de lado conocidas por los nombres de lado en la proporción. Deje que la longitud del lado desconocido sea n.
\(\dfrac{n}{2} = \dfrac{6}{1.5}\)
Resuelve para n usando multiplicación cruzada.
\(2 \cdot 6 = 1.5 \cdot n\)
\(12 = 1.5n\)
\(8 = n\)
Este proceso es bastante sencillo, pero tenga cuidado de que sus proporciones representen lados correspondientes, recordando que los lados correspondientes son ángulos correspondientes opuestos.
Solución de problemas de aplicación que involucran triángulos similares
Aplicar conocimientos de triángulos, similitud y congruencia puede ser muy útil para resolver problemas en la vida real. Así como puedes resolver las longitudes faltantes de un triángulo dibujado en una página, puedes usar triángulos para encontrar distancias desconocidas entre ubicaciones u objetos.
Consideremos el ejemplo de dos árboles y sus sombras. Supongamos que el sol está brillando sobre dos árboles, uno que mide 6 pies de altura y el otro cuya altura es desconocida. Al medir la longitud de cada sombra en el suelo, puedes usar la similitud triangular para encontrar la altura desconocida del segundo árbol.
Primero, descubramos dónde están los triángulos en esta situación. Los propios árboles crean un par de lados correspondientes. Las sombras proyectadas en el suelo son otro par de lados correspondientes. El tercer lado de estos triángulos similares imaginarios va desde la parte superior de cada árbol hasta la punta de su sombra en el suelo. Esta es la hipotenusa del triángulo.
Si sabes que los árboles y sus sombras forman triángulos similares, puedes establecer una proporción para encontrar la altura del árbol.
Cuando el sol está en cierto ángulo en el cielo, un árbol de 6 pies proyectará una sombra de 4 pies. ¿Qué tan alto es un árbol que proyecta una sombra de 8 pies?
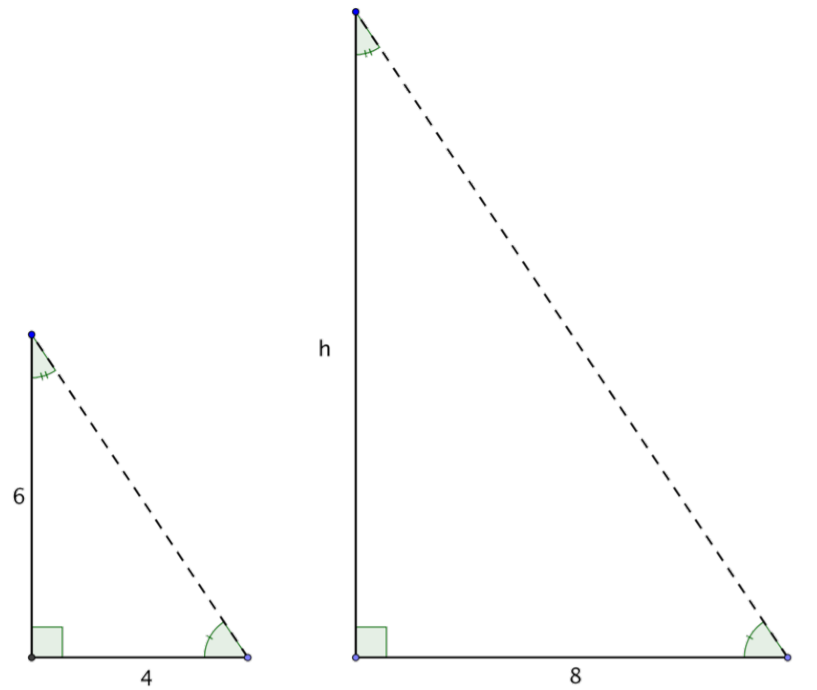
Solución
Las medidas de ángulo son las mismas, por lo que los triángulos son triángulos similares. Al ser triángulos similares, puedes usar proporciones para encontrar el tamaño del lado faltante.
\(\dfrac{\text{Tree 1}}{\text{Tree 2}} = \dfrac{\text{Shadow 1}}{\text{Shadow 2}}\)
Establecer una proporción comparando las alturas de los árboles y la longitud de sus sombras.
Sustituto en las longitudes conocidas. Llame al árbol faltante altura h.
\(\dfrac{6}{h} = \dfrac{4}{8}\)
Resuelve para h usando multiplicación cruzada.
\(6 \cdot 8 = 4h\)
\(48 = 4h\)
\(12 = h\)
Respuesta: El árbol mide 12 pies de altura.
Resumen
Los triángulos son una de las formas básicas en el mundo real. Los triángulos se pueden clasificar por las características de sus ángulos y lados, y los triángulos se pueden comparar en función de estas características. La suma de las medidas de los ángulos interiores de cualquier triángulo es de 180º. Los triángulos congruentes son triángulos del mismo tamaño y forma. Tienen lados correspondientes de igual longitud y ángulos correspondientes de la misma medida. Triángulos similares tienen la misma forma, pero no necesariamente del mismo tamaño. Las longitudes de sus lados son proporcionales. El conocimiento de los triángulos puede ser útil para resolver problemas del mundo real.
1. Escaleno obtuso; este triángulo tiene vértices P, Q y R, un ángulo (ángulo Q) que está entre 90º y 180º, y lados de tres longitudes diferentes.
2. ∆ABC y ∆DEF no son similares ni congruentes; no se sabe que las medidas de ángulo correspondientes sean iguales como lo demuestra la ausencia de marcas de congruencia en los ángulos. Además, las proporciones de los lados correspondientes no son iguales:\( \dfrac{6.5}{5} = \dfrac{6.5}{5} \neq \dfrac{5}{5} \)
6.1.3: Teorema de Pitágoras
- Usa el Teorema de Pitágoras para encontrar el lado desconocido de un triángulo rectángulo.
- Resolver problemas de aplicación relacionados con el Teorema de Pitágoras.
Introducción
Hace mucho tiempo, un matemático griego llamado Pitágoras descubrió una propiedad interesante sobre los triángulos rectos: la suma de los cuadrados de las longitudes de cada una de las patas del triángulo es la misma que la cuadrada de la longitud de la hipotenusa del triángulo. Esta propiedad, que tiene muchas aplicaciones en la ciencia, el arte, la ingeniería y la arquitectura, ahora se llama Teorema de Pitágoras.
Echemos un vistazo a cómo este teorema puede ayudarte a aprender más sobre la construcción de triángulos. Y lo mejor, ni siquiera tienes que hablar griego para aplicar el descubrimiento de Pitágoras.
El teorema de Pitágoras
Pitágoras estudió los triángulos rectos, y las relaciones entre las piernas y la hipotenusa de un triángulo rectángulo, antes de derivar su teoría.
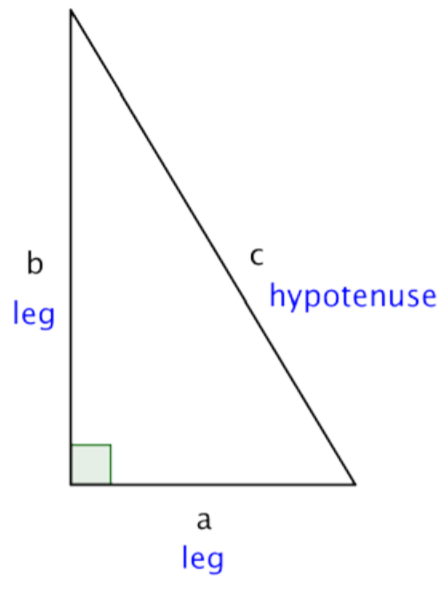
Si a y b son las longitudes de las patas de un triángulo rectángulo y c es la longitud de la hipotenusa, entonces la suma de los cuadrados de las longitudes de las patas es igual al cuadrado de la longitud de la hipotenusa.
Esta relación está representada por la fórmula:\(a^2 + b^2 = c^2\)
En el cuadro de arriba, es posible que hayas notado la palabra “cuadrado”, así como los pequeños 2s a la parte superior derecha de las letras en\(a^2 + b^2 = c^2\). Cuadrar un número significa multiplicarlo por sí mismo. Entonces, por ejemplo, para cuadrar el número\(5\) multiplicas\(5 \cdot 5\), y para cuadrar el número\(12\), multiplicas\(12 \cdot 12\). Algunos cuadrados comunes se muestran en la siguiente tabla.
| Número | Número de veces en sí | Cuadrado |
| 1 | \(1^2 = 1 \cdot 1\) | 1 |
| 2 | \(2^2 = 2 \cdot 2\) | 4 |
| 3 | \(3^2 = 3 \cdot 3\) | 9 |
| 4 | \(4^2 = 4 \cdot 4\) | 16 |
| 5 | \(5^2 = 5 \cdot 5\) | 25 |
| 10 | \(10^2 = 10 \cdot 10\) | 100 |
Cuando ves la ecuación\(a^2 + b^2 = c^2\), puedes pensar en esto como “la longitud del lado a veces en sí mismo, más la longitud del lado b veces en sí mismo es la misma que la longitud del lado c veces en sí mismo”.
Probemos todo el teorema de Pitágoras con un triángulo rectángulo real.
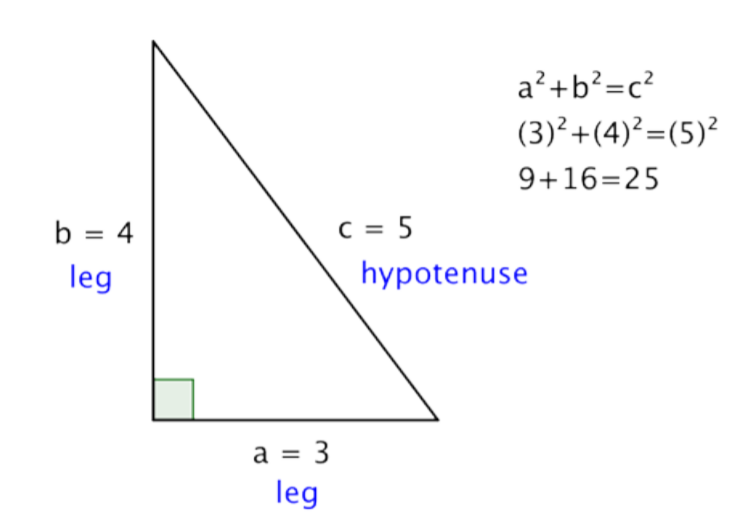
Este teorema es válido para este triángulo derecho—la suma de los cuadrados de las longitudes de ambas patas es la misma que el cuadrado de la longitud de la hipotenusa. Y, de hecho, es cierto para todos los triángulos correctos.
El Teorema de Pitágoras también se puede representar en términos de área. En cualquier triángulo rectángulo, el área del cuadrado dibujado a partir de la hipotenusa es igual a la suma de las áreas de los cuadrados que se dibujan de las dos patas. Puedes ver esto ilustrado a continuación en el mismo triángulo rectángulo 3-4-5.
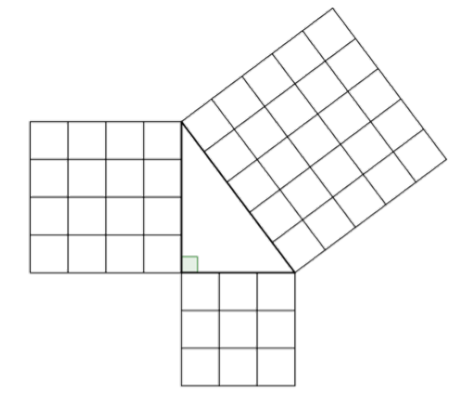
Tenga en cuenta que el Teorema de Pitágoras solo funciona con triángulos rectos.
Encontrar la longitud de la hipotenusa
Puedes usar el Teorema de Pitágoras para encontrar la longitud de la hipotenusa de un triángulo rectángulo si conoces la longitud de los otros dos lados del triángulo, llamados las piernas. Dicho de otra manera, si conoces las longitudes de a y b, puedes encontrar c.
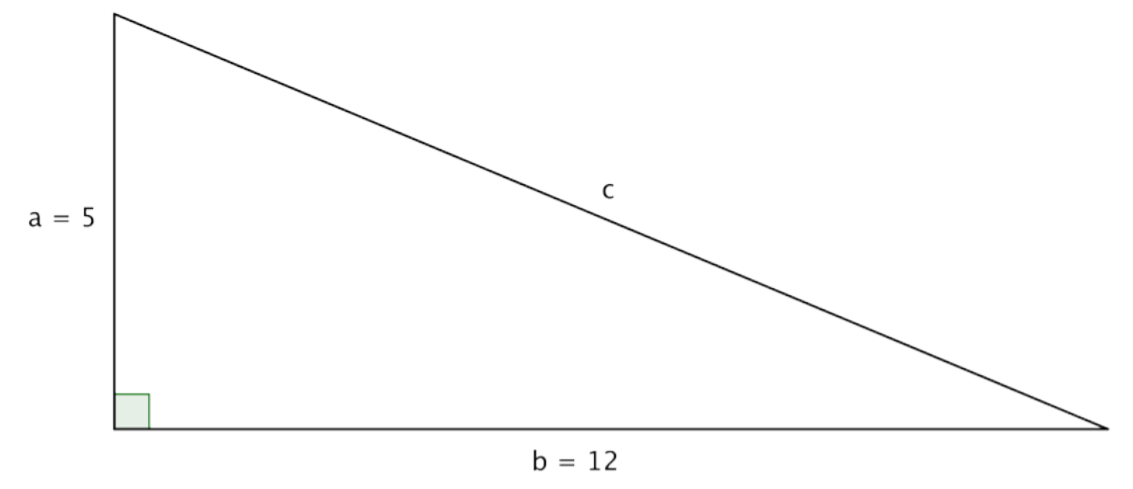
En el triángulo anterior, se le dan medidas para las piernas a y b: 5 y 12, respectivamente. Se puede utilizar el Teorema de Pitágoras para encontrar un valor para la longitud de c, la hipotenusa.
El Teorema de Pitágoras.
\(a^2 + b^2 = c^2\)
Sustituir valores conocidos por a y b.
\((5)^2 + (12)^2 = c^2\)
Evaluar.
\(25 + 144 = c^2\)
Simplificar. Para encontrar el valor de c, piense en un número que, cuando se multiplica por sí mismo, equivale a 169. ¿Funciona 10? ¿Qué tal 11? ¿12? ¿13? (Puede usar una calculadora para multiplicar si los números no están familiarizados).
\(169 = c^2\)
La raíz cuadrada de 169 es 13.
\(c = 13\)
Usando la fórmula, se encuentra que la longitud de c, la hipotenusa, es 13.
En este caso, desconocía el valor de c —se le dio el cuadrado de la longitud de la hipotenusa, y tuvo que averiguarlo a partir de ahí. Cuando se le da una ecuación como\(169 = c^2\) y se le pide que encuentre el valor de c, esto se llama encontrar la raíz cuadrada de un número. (Observe que encontró un número, c, cuyo cuadrado era 169.)
Encontrar una raíz cuadrada requiere algo de práctica, pero también requiere conocimiento de multiplicación, división y un poco de prueba y error. Mira la tabla a continuación.
| Número\(x\) | Número\(y\) que, cuando se multiplica por sí mismo, es igual a número\(x\) | Raíz cuadrada\(y\) |
| 1 | \(1 \cdot 1\) | 1 |
| 4 | \(2 \cdot 2\) | 2 |
| 9 | \(3 \cdot 3\) | 3 |
| 16 | \(4 \cdot 4\) | 4 |
| 25 | \(5 \cdot 5\) | 5 |
| 100 | \(10 \cdot 10\) | 10 |
Es un buen hábito familiarizarse con los cuadrados de los números de 0 a 10, ya que estos surgen frecuentemente en las matemáticas. Si puedes recordar esos números cuadrados, o si puedes usar una calculadora para encontrarlos, entonces encontrar muchas raíces cuadradas comunes será solo cuestión de recordar.
¿Para cuál de estos triángulos es\((3)^2 + (3)^2 = r^2\)?
A) B)
B)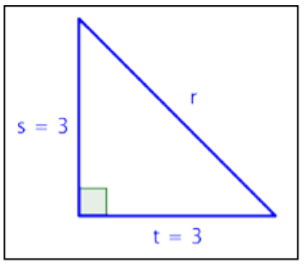
C)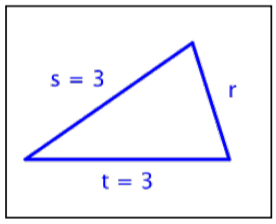 D)
D)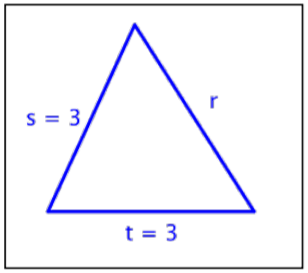
Encontrar la longitud de una pierna
Puedes usar la misma fórmula para encontrar la longitud de la pierna de un triángulo rectángulo si te dan medidas para las longitudes de la hipotenusa y la otra pierna. Considera el siguiente ejemplo.
Encuentra la longitud del lado a en el triángulo de abajo. Use una calculadora para estimar la raíz cuadrada a un decimal.
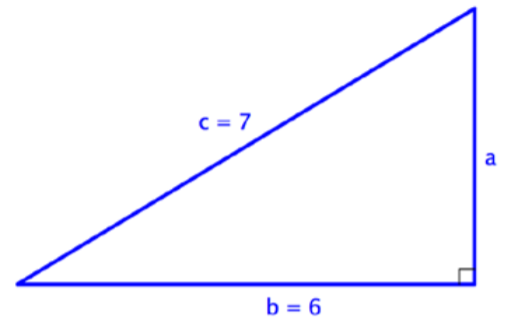
Solución
En este triángulo rectángulo, se le dan las medidas para la hipotenusa, c, y una pierna, b. La hipotenusa siempre es opuesta al ángulo recto y siempre es el lado más largo del triángulo.
\(a\)=?
\(b\)= 6
\(c\)= 7
Para encontrar la longitud de la pata a, sustituya los valores conocidos en el Teorema de Pitágoras.
\(a^2 + b^2 = c^2\)
\(a^2 + 6^2 = 7^2\)
Resolver para\(a^2\). Piensa: ¿qué número, cuando se agrega al 36, te da 49?
\(a^2 + 36 = 49\)
\(a^2 = 13\)
Usa una calculadora para encontrar la raíz cuadrada de 13. La calculadora da una respuesta de 3.6055..., que puedes redondear a 3.6. (Ya que estás aproximando, usas el símbolo ≈.)
\(a ≈ 3.6\)
Respuesta: a ≈ 3.6
¿Cuál de las siguientes utiliza correctamente el Teorema de Pitágoras para encontrar el lado faltante,\(x\)?
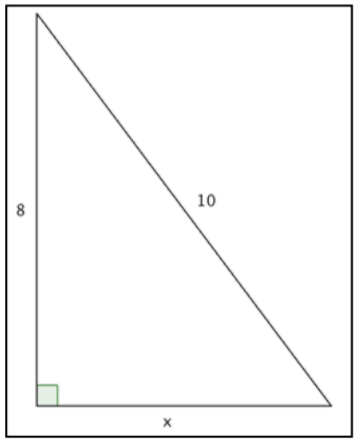
A)\(8^2 + 10^2 = x^2\)
B)\(x + 8 = 10\)
C)\(x^2 + 8^2 = 10^2\)
D)\(x^2 + 10^2 = 8^2\)
Usando el teorema de Pitágoras para resolver problemas del mundo real
El Teorema de Pitágoras es quizás una de las fórmulas más útiles que aprenderás en matemáticas porque hay tantas aplicaciones del mismo en entornos del mundo real. Los arquitectos e ingenieros utilizan esta fórmula ampliamente cuando construyen rampas, puentes y edificios. Mira los siguientes ejemplos.
Los dueños de una casa quieren convertir una escalera que conduce desde el suelo hasta su porche trasero en una rampa. El porche está a 3 pies del suelo, y debido a las regulaciones de construcción, la rampa debe comenzar a 12 pies de distancia de la base del porche. ¿Cuánto tiempo durará la rampa?
Usa una calculadora para encontrar la raíz cuadrada, y redondea la respuesta a la décima más cercana.
Solución
Para resolver un problema como este, muchas veces tiene sentido dibujar un diagrama simple que muestre dónde se encuentran las piernas y la hipotenusa del triángulo.
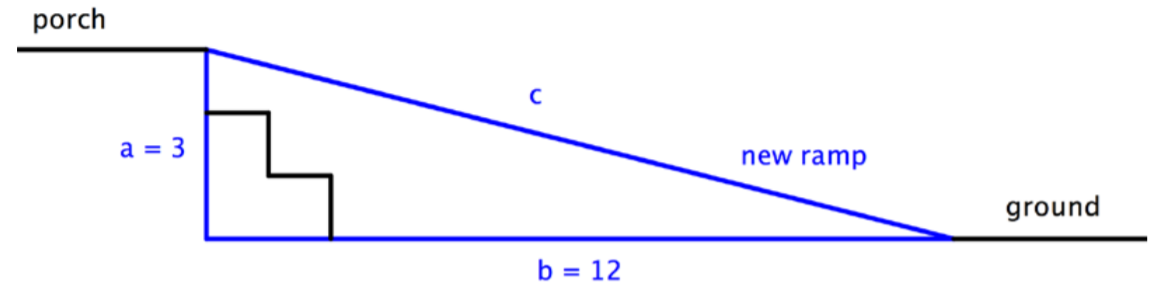
Identificar las piernas y la hipotenusa del triángulo. Sabes que el triángulo es un triángulo rectángulo ya que el suelo y la parte elevada del pórtico son perpendiculares—esto significa que puedes usar el Teorema de Pitágoras para resolver este problema. Identificar a, b y c.
\(a\)= 3
\(b\)= 12
\(c\)=?
Usa el Teorema de Pitágoras para encontrar la longitud de c.
\(a^2 + b^2 = c^2\)
\(3^2 + 12^2 = c^2\)
\(9 + 144 = c^2\)
\(153 = c^2\)
Use una calculadora para encontrar c.
\(12.4 = c^2\)
La raíz cuadrada de 153 es 12.369..., así puedes redondear eso a 12.4.
Respuesta: La rampa tendrá 12.4 pies de largo.
Un velero tiene una vela grande en forma de triángulo rectángulo. El borde más largo de la vela mide 17 yardas, y el borde inferior de la vela es de 8 yardas. ¿Qué tan alta es la vela?
Solución
Dibuja una imagen que te ayude a visualizar el problema. En un triángulo rectángulo, la hipotenusa siempre será el lado más largo, por lo que aquí debe ser de 17 yardas. El problema también te dice que el borde inferior del triángulo es de 8 yardas.

Configurar el Teorema de Pitágoras.
\(a^2 + b^2 = c^2\)
\(a^2 + 8^2 = 17^2\)
\(a^2 + 64 = 289\)
\(a^2 = 225\)
\(15 \cdot 15 = 225\), entonces
\(a = 15\)
Respuesta: La altura de la vela es de 15 yardas.
Resumen
El Teorema de Pitágoras establece que en cualquier triángulo rectángulo, la suma de los cuadrados de las longitudes de las patas del triángulo es la misma que la cuadrada de la longitud de la hipotenusa del triángulo. Este teorema está representado por la fórmula 222 abc + =. En pocas palabras, si conoces las longitudes de dos lados de un triángulo rectángulo, puedes aplicar el Teorema de Pitágoras para encontrar la longitud del tercer lado. Recuerda, este teorema sólo funciona para triángulos rectos.
1. B) ; esto es un triángulo rectángulo; cuando sumas los cuadrados de las longitudes de los lados, obtienes el cuadrado de la longitud de la hipotenusa.
; esto es un triángulo rectángulo; cuando sumas los cuadrados de las longitudes de los lados, obtienes el cuadrado de la longitud de la hipotenusa.
2. C)\(x^2 + 8^2 = 10^2\); en este triángulo, la hipotenusa tiene longitud\(10\), y las piernas tienen longitud\(8\) y\(x\). Sustituyendo al Teorema de Pitágoras tienes:\(x^2 + 8^2 = 10^2\); esta ecuación es la misma que\(x^2 + 64 = 100\), o\(x^2 = 36\). ¿Qué número, veces en sí mismo, es igual\(36\)? Eso haría\(x = 6\).


